Аннотация
Чернышов Д.Н., Грищенко О.С., Григорьев А.В. Использование метода конечных элементов для физических расчетов в САПР. Рассмотрена проблема физических расчетов в виртуальных моделях проектов. Рассмотрен метод конечных элементов в общем виде.
Общая постановка проблемы
Одной из ключевых особенностей САПР является возможность моделирования физических процессов, не прибегая к созданию реального прототипа детали. Потребность в решении подобных задач возникает в системах автоматизированного конструирования для моделирования поведения изделия в цифровом виде. Типичными примерами процессов, моделирование которых на компьютере позволяет значительно сократить расходы на испытания, являются продувка в аэродинамической трубе или аварийные испытания (краш-тесты). Однако какими методами достигаются такие возможности и какой из них лучший?
В этой работе будет рассмотрен конечно-элементный анализ как один из лучших методов моделирования физических процессов
Метод конечных элементов (МКЭ)
Конечно-элементный анализ широко применяется при решении задач механики деформируемого твердого тела, теплообмена, гидро- и газодинамики, а также других областей физики. Он основан на использовании математического метода конечных элементов [1].
Метод конечных элементов позволяет приближенно численно решать широкий спектр физических проблем, которые математически формулируются в виде системы дифференциальных уравнений или в вариационной постановке. Этот метод можно использовать для анализа напряженно деформированного состояния конструкций, для термического анализа, для решения гидро-газодинамических задач и задач электродинамики.
Сейчас МКЭ является одним из наиболее популярных инструментов исследования характеристик инженерных конструкций, подвергаемых различным нагрузкам. Традиционные методы, предполагающие строгое теоретическое обоснование, могут использоваться только для ограниченного класса задач и особых условий нагрузки. Они часто нуждаются в модификации, причем приходится контролировать их применимость к решению поставленной задачи. Неуверенность конструкторов в достоверности полученных результатов заставляет их повышать предельные нагрузки, что приводит к включению в конструкцию дополнительных крепежных секций, перерасходу материалов и повышению общей стоимости изделия.
МКЭ позволяет конструктору решать задачи расчета сложных деталей путем разбиения их на более мелкие части – конечные элементы. Эти элементы иногда называют дискретными, а процесс их выделениядискретизацией формы детали.
После разбивки дальнейшие расчеты проводятся для отдельных конечных элементов, каждый из них вносит свой вклад в характеристику прочности детали. Точки, ограничивающие элемент, называют узлами, которые вместе с проходящими через них линиями образуют конечную элементную сетку.
Для 2D-областей наиболее часто используются элементы в форме треугольника и четырехугольника. При этом элементы могут иметь как прямо-, так и криволинейные границы, что позволяет с достаточной степенью точности аппроксимировать границу любой формы. Для 3Dобластей наиболее употребимыми являются элементы в форме тетраэдра и параллелепипеда, которые также могут иметь прямо- и криволинейные границы [2].
МКЭ состоит из 5 этапов:
1. Выделение конечных элементов.
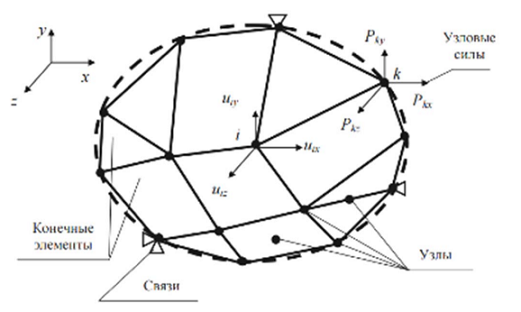
Рисунок 1 – Выделение конечных элементов
Это один из наиболее важных этапов МКЭ, т.к. от качества разбиения во многом зависит точность полученных результатов (рис. 1).
Например, разбиение на двумерные элементы, близкие по форме к равносторонним треугольникам, обеспечивает лучшие результаты по сравнению с разбиением на вытянутые треугольники. Возможность легко изменять размеры элементов позволяет без труда учитывать свойства материалов, концентрацию напряжения, температурные градиенты и т.д. Разбиение области на элементы обычно начинают от ее границы с целью получения наиболее точной аппроксимации формы границы, затем выполняют разбиение внутренних областей. Часто разбиение области на элементы выполняют в несколько этапов: сначала область делится на достаточно большие подобласти, границы между которыми проходят там, где изменяются свойства материалов, геометрия, приложенная нагрузка и др. Затем каждая подобласть делится на элементы, причем резкого изменения размеров конечных элементов на границах подобластей лучше избегать.
2. Нумерация узлов элементов.
Порядок нумерации имеет в данном случае существенное значение, так как влияет на эффективность последовательных вычислений. Дело в том, что матрица коэффициентов системы множества алгебраических уравнений, к которым приводит МКЭ – сильно разряженная матрица ленточной структуры. Ненулевые элементы матрицы располагаются параллельно главной диагонали. Целое число, являющееся максимальной разностью между номерами ненулевых элементов в строке, называется шириной полосы. Чем меньше ширина полосы, тем меньший объем памяти требуется для хранения матрицы при реализации МКЭ и тем меньше затраты машинного времени на решение результирующей системы уравнений. Ширина полосы зависит от количества степеней свободы узлов и способа нумерации последних. При нумерации узлов предпочтителен способ, обеспечивающий минимальную разницу между номерами узлов в каждом отдельном элементе.
Если максимальная разность между номерами узлов для отдельного элемента обозначить через K, а количество степеней свободы через S, то ширина полосы L=(K+1)*S.
В некоторых случаях уменьшение числа K может быть достигнуто последовательной нумерацией узлов при движении в направлении минимального размера рассматриваемой области. Рациональная нумерация уменьшает необходимый объем памяти почти в 3 раза.
Информация о способе разбиения области на конечные элементы и нумерация узлов является исходной для всех следующих этапов алгоритмов МКЭ при реализации методов САПР. При этом требуется указывать не только номер, но и координаты каждого узла и принадлежность его к определенным конечным элементам. Такого рода информация называется топологической и содержит примерно в 6 раз больше цифр, чем количество узлов системы. При описании области, разбитой на конечные элементы, необходимо задавать тип конечного элемента, его порядковый номер, номера узлов элемента, координаты узлов, информацию о соединении элементов, значении физических параметров объекта в пределах конечного элемента.
3. Определение аппроксимирующей функции для каждого элемента.
На этом этапе ищем непрерывную аппроксимирующую функцию кусочно-непрерывных, определенную на множестве конечных элементов. Эту процедуру нужно выполнить один раз для типичного элемента области безотносительно к его топологическому положению в ней. Полученная функция используется для всех остальных элементов области того же вида. Эта особенность является важным аспектом МКЭ. Благодаря ей элементы с однажды определенными функциями легко включаются в библиотеку элементов соответствующего программного комплекса и далее используется для решения разнообразных задач. В качестве аппроксимирующей функции элементов чаще всего используются полиномы, которые разбираются так, чтобы обеспечить непрерывность искомой функции в узлах и на границах элементов.
4. Объединение конечных элементов в ансамбль.
На этом этапе уравнения, относящиеся к отдельным элементам, объединяются в ансамбль, т.е. в систему алгебраических уравнений. При этом узлы перенумеруются.
5. Решение полученной системы алгебраических уравнений.
Реальная конструкция аппроксимируется сотнями конечных элементов, и, следовательно, появляются системы уравнений с сотнями и тысячами неизвестных, которые нужно решить. Решение таких систем - главная проблема реализации МКЭ. Методы решений зависят от размеров разрешающей системы уравнений. В связи с большой размерностью и сильной разряженностью матрицы коэффициентов для реализации МКЭ САПР разработаны специальные способы хранения матрицы жесткости, позволяющей уменьшить необходимый для этого объем памяти. Матрицы жесткости используются в каждом методе прочностного расчета, используя конечную элементную сетку [2].
Возможности МКЭ в САПР Catia
Приведем возможности МКЭ на примере моделирования прочностных расчетов в САПР Catia [3] [4].
Для анализа на прочность предназначено приложение Generative Part Structural Analysis модуля «Анализ и моделирование». Модуль можно использовать, не имея специальных знаний в области расчетов методом конечных элементов. Схема его использования сведена к простейшим процедурам:
- присвоения материала;
- указания мест и условий закрепления;
- указания мест и условий нагружения.
После автоматической генерации сетки конечных элементов, выбора оптимального расчетного метода и собственно расчета, модуль предоставляет результаты в наглядной и легко понимаемой форме. На основании этих результатов конструктор может сделать вывод о том, как следует изменить деталь, чтобы оптимизировать ее механические характеристики.
Можно посмотреть нагрузку, которая оказывается на разные части детали. Для этого необходимо использовать инструмент «Von Mises Stress». После выбора этого инструмента деталь окрасится в цвета, соответствующие нагрузке и появится шкала, сопоставляющая цвет со значением нагрузки как показано на рисунке 2.

Рисунок 2 – Результат применения инструмента «Von Mises Stress»
Можно также посмотреть нагрузку и смещение в конечных точках детали. Для того чтобы посмотреть смещение точек детали используется инструмент «Desplacement».
Результат применения этого инструмента представлен на рисунке 3.

Рисунок 3 – Результат применения инструмента «Desplacement»
Выводы
Как уже было сказано ранее, метод конечных элементов является одним из самых оптимальных на сегодняшний день способов моделировать физические процессы в САПР. Однако, развитию этого метода еще есть куда стремиться. Например, стоит оптимизировать использование оперативной памяти для повышения максимального количества моделируемых узлов.
Список использованной литературы
1. Методы расчета физических процессов в САПР [Электронный ресурс]. Режим доступа:
https://studbooks.net/2194686/tehnika/metody_rascheta_mehanicheskih_protsessov_sapr
2. Системы автоматизированного анализа [Электронный ресурс]. Режим доступа:
https://studfile.net/preview/987775/page:20/
3. Generative Structural Analysis [Электронный ресурс]. Режим
доступа: http://www.catiadesign.org/_doc/v5r14/catpdfestug_C2/estug.pdf
4. Entering the Generative Structural Analysis Workbench [Электронный ресурс]. Режим доступа:
http://catiadoc.free.fr/online/CATIAfr_C2/estugCATIAfrs.htm