Аннотация
Чернышов Д.Н., Григорьев А.В., Воробьев Л.О. Расширение функциональных возможностей подсистем моделирования и инжиниринга (САЕ) в современных САПР. Описан принцип работы метода конечных элементов. Рассмотрены возможности улучшения метода конечных элементов при помощи программирования в ограничениях.
Общая постановка проблемы
CAE (Computer-aided engineering) представляет из себя комплекс программных продуктов, которые могут дать пользователю характеристику того, как в реальности будет вести себя разработанная на компьютере модель изделия. При помощи CAE инженер может достаточно точно оценить работоспособность изделия, не прибегая при этом к значительным временным и денежным затратам.[1]
В свою очередь, CAE классифицируются на следующие типы систем:
- Системы полнофункционального инженерного анализа, обладающие мощными средствами, большими хранилищами типов для сеток конечных элементов, а также всевозможных физических процессов. В них предусмотрены собственные средства моделирования геометрии. Более того, в них есть возможность импорта через промышленные стандарты Parasolid и ACIS. Самыми известными подобными системами считаются ANSYS/Multiphysics, AI*NASTRAN и MSC.NASTRAN.;
- Системы инженерного анализа, встроенные в тяжелые САПР. Они имеют значительно менее мощные средства анализа, но при этом они ассоциативны с геометрией, поэтому отслеживают изменения модели. Расчетные данные структурированы и интегрированы в общую систему проектирования САПР. К таким системам относятся Pro/MECHANICA для Pro/ENGINEER, Unigraphics NX CAE для Unigraphics NX, Extensive Digital Validation (CAE) для I-deas, Catia CAE для CATIA;
- Системы инженерного анализа среднего уровня. Они не имеют мощных расчетных возможностей и хранят данные в собственных форматах. Некоторые включают в состав встраиваемый интерфейс в CAD-системы, другие считывают геометрию из CAD. К первым относятся COSMOS/Works, COSMOS/Motion, COSMOS/FloWorks для SolidWorks Трехмерная проектная среда, ко вторым — visualNastran, Procision.
В своей работе CAE используют различные математические расчеты: метод конечных элементов, метод конечных объемов, метод конечных разностей.
В данной статье будет рассмотрен метод конечных элементов и возможности его улучшения посредством интервальной математики.
Метод конечных элементов (МКЭ) — это численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики, электродинамики и топологической оптимизации.
Суть метода заключена в его названии. Область, в которой ищется решение дифференциальных уравнений, разбивается на некоторое количество подобластей (элементов). В каждом из этих элементов произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (в узлах) являются решением задачи и заранее неизвестны. Коэффициенты аппроксимирующих функций обычно находятся из условия равенства значений соседних функций на границах между элементами, то есть в узлах. Затем эти коэффициенты выражаются через значения функций в узлах элементов. Составляется система линейных алгебраических уравнений, в которой количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов и ограничивается только возможностями ЭВМ. Так как каждый из элементов связан с ограниченным количеством соседних, система линейных алгебраических уравнений имеет разрежённый вид, что существенно упрощает её решение.
Если говорить в матричных терминах, то собираются так называемые матрицы жёсткости и масс. Далее на эти матрицы накладываются граничные условия (например, при условиях Неймана в матрицах не меняется ничего, а при условиях Дирихле из матриц вычёркиваются строки и столбцы, соответствующие граничным узлам, так как в силу краевых условий значение соответствующих компонент решения известно). Затем собирается система линейных уравнений и решается одним из известных методов.
С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти.
Метод получил широкое применение при проектировании сооружений, а также при моделировании моделей движения, к примеру, грунта. За рубежом метод почти сразу начал повсеместно использоваться, а в России — только в 2000-х годах сменил вариационно-разностные, конечно-разностные методы.
Метод конечных элементов возник из необходимости новых путей решения задач строительной механики и теории упругости в 1930-х годах. Одними из основоположников идей, лежащих в основе МКЭ, считаются Александр Хренников и Рихард Курант. Их работы опубликованы в 1940-х годах. Впервые эффективность МКЭ была продемонстрирована в 1944 году Иоаннисом Аргирисом, который реализовал метод с применением ЭВМ.
В Китае в 1950-х годах Кан Фэн предложил численный метод решения дифференциальных уравнений в частных производных для расчета конструкций плотин. Этот метод был назван методом конечных разностей на основе вариационного принципа, что может рассматриваться как еще один независимый способ реализации метода конечных элементов.
Хотя перечисленные подходы различаются между собой в деталях, они имеют одну общую черту: дискретизация непрерывной области сеткой в набор дискретных поддоменов, обычно называемых элементами.
Дальнейшее развитие метода конечных элементов связано также с решением задач космических исследований в 1950-х годах.
В СССР распространение и практическая реализация МКЭ в 1960-х годах связана с именем Леонарда Оганесяна.
Существенный толчок в своём развитии МКЭ получил в 1963 году после того, как было доказано, что его можно рассматривать как один из вариантов распространённого в строительной механике метода Рэлея — Ритца, который путём минимизации потенциальной энергии сводит задачу к системе линейных уравнений равновесия. После того, как была установлена связь МКЭ с процедурой минимизации, он стал применяться к задачам, описываемым уравнениями Лапласа или Пуассона. Область применения МКЭ значительно расширилась, когда было установлено (в 1968 году), что уравнения, определяющие элементы в задачах, могут быть легко получены с помощью вариантов метода взвешенных невязок, таких как метод Галёркина или метод наименьших квадратов. Это сыграло важную роль в теоретическом обосновании МКЭ, так как позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений.
С развитием вычислительных средств возможности метода постоянно расширяются, также расширяется и класс решаемых задач. В настоящее время предложено большое количество реализаций метода конечных элементов при моделировании процессов диффузии, теплопроводности, гидродинамики, механики, электродинамики и др.
Метод конечных элементов сложнее метода конечных разностей в реализации. Однако, у МКЭ есть ряд преимуществ, проявляющихся на реальных задачах: произвольная форма обрабатываемой области; сетку можно сделать более редкой в тех местах, где особая точность не нужна.
Долгое время широкому распространению МКЭ мешало отсутствие алгоритмов автоматического разбиения области на «почти равносторонние» треугольники (погрешность, в зависимости от вариации метода, обратно пропорциональна синусу или самого острого, или самого тупого угла в разбиении). Впрочем, эту задачу удалось успешно решить (алгоритмы основаны на триангуляции Делоне), что дало возможность создавать полностью автоматические конечноэлементные САПР.
Исследования
В настоящее время проблемой МКЭ можно считать громоздкость задач данного типа. С этим может помочь программирование в ограничениях.
Программирование в ограничениях является по сути своей максимально декларативным и основано на описании модели задачи, а не алгоритма ее решения. Модель специфицируется в виде неупорядоченной совокупности отношений, которые соответствуют связям, существующим между параметрами задачи. Эти отношения, называемые «ограничениями», могут иметь вид уравнений, неравенств, логических выражений и т. п.
В общем виде постановка задачи в парадигме программирования в ограничениях выглядит следующим образом. На переменные (x1, x2 ..., xn), областями значений которых являются множества (X1 , X2 , ..., Xn) , заданы ограничения Ci (x1 , x2 , ..., xn), i=1, k. Нужно найти такие наборы значений (a1 , a2 , ..., an) (ai принадлежит Xi), которые бы удовлетворяли всем ограничениям одновременно.
Такую постановку задачи называют «проблема удовлетворения ограничений», а для ее решения используют различные алгоритмы и методы. В частном виде проблема удовлетворения ограничений может быть сформулирована как система уравнений с числовыми параметрами, а для ее решения можно использовать стандартные численные методы. Однако при попытке решить многие реальные задачи эти методы оказываются неприменимыми, особенно в случаях, когда модель включает и нечисловые параметры, а начальные данные задаются приблизительно в виде множеств и интервалов, содержащих допустимые значения.[4]
Одним из наиболее развитых и практически значимых подходов, относящихся к программированию в ограничениях, являются недоопределенные модели.
Метод недоопределенных моделей (Н-моделей) был предложен в начале 80-x годов для представления и обработки неполностью определенных знаний. Вначале рассматриваемый как оригинальный метод из области искусственного интеллекта, постепенно он трансформировался в прикладную технологию программирования в ограничениях. Технология недоопределенных моделей выделяется среди других подходов вычислительной мощностью, универсальностью и эффективностью. Фактически, она является единственной технологией, которая позволяет решать задачу удовлетворения ограничений в самой что ни на есть общей постановке.
К настоящему моменту на базе недоопределенных моделей создана многоуровневая технология программирования, которая позволяет решать качественно новые классы задач в таких областях, как экономика, инженерные расчеты, календарное планирование, вычислительная математика, САПР, ГИС и т. п.
В основе аппарата недоопределенных моделей лежат следующие понятия:
- Недоопределенная переменная – некоторое непустое подмножество, содержащее внутри себя значение-денотат, ввиду недостатка информации остающееся неизвестным; доступная оценка реального значения;
- Недоопределенное расширение – любая конечная система подмножеств множества Х, замкнутая относительно операции пересечения и содержащая весь универсум и пустое множество. Для одного и того же универсума могут существовать несколько различных недоопределенных расширений.[5]
Рассмотрим некоторые виды недоопределенных расширений, использующиеся в программных технологиях, базирующихся на аппарате Н-моделей:
1) Наиболее простым является недоопределенное расширение, в котором каждый его элемент представлен точным значением (*X = X Single):
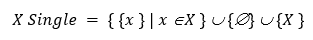
Данное недоопределенное расширение добавляет в обычный универсум два специальных значения: «не определено» и «противоречие».
2) Перечислимое недоопределенное расширение представляется множеством всех подмножеств (обозначим его как 2^X):
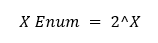
Данное недоопределенное расширение можно применять лишь к конечным универсумам.
В случае, когда X является решеткой (множеством с определенными на нем ассоциативными и коммутативными операциями, подчиняющимися законам поглощения и идемпотентности), можно задать такие виды недоопределенных расширений X, как интервалы и мультиинтервалы.
3) Интервальное недоопределенное расширение:
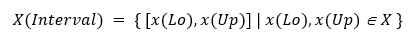
Здесь x(Lo) обозначает нижнюю, а x(Up) — верхнюю границу интервала. Пустое множество представляется любым интервалом [x(Lo), x(Up)], где (x(Lo)>x(Up)).
Мультиинтервальное недоопределенное расширение:
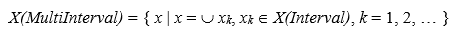
Некоторые свойства обычных операций существенно меняются в соответствующих недоопределенных расширениях. Как пример рассмотрим хорошо известное свойство аддитивных операций над числами (целых или вещественных), что сумма любого числа и обратного ему равна единственному нулевому элементу (5).
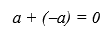
Далее рассмотрим в качестве недоопределенного расширения множества чисел недоопределенное расширение Interval, а соответствующие недоопределенные расширения операций минус (*-) и плюс (*+) определены согласно известным правилам интервальной арифметики. Таким образом, недоопределенное расширение унарного минуса имеет следующий вид:
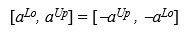
Недоопределенное расширение сложения (a = b *+ c) вычисляется подобным образом:
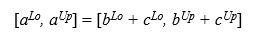
В таком случае, недоопределенное расширение выражения (5) имеет следующий вид:
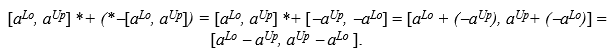
Таким образом, если нижняя и верхняя границы недоопределенного числа не совпадают, интервал [aLo - aUp, aUp - aLo] всего лишь содержит в себе нулевой элемент, но не равен ему в точности.
Делая вывод из выше сказанного, в недоопределенных моделях весьма существенно, в каком виде представлены условия задачи, что вполне может быть полезным при использовании метода конечных элементов.
Выводы
Интеграция программирования в ограничениях позволит методу конечных элементов работать не только с дискретными значениями, но и с интервальной математикой. Предполагается, что это может улучшить его работу в некоторых моделируемых ситуациях.
Список использованной литературы
1.CAE системы инженерного анализа. [Электронный ресурс]. Режим доступа: https://www.tadviser.ru/index.php/Статья:CAE_Системы_инженерного_анализа
2. Основные этапы решения задач методом конечных элементов. САПР конструктора машиностроителя. [Электронный ресурс]. Режим доступа: https://studref.com/605503/tehnika/osnovnye_etapy_resheniya_zadach_metodom_konechnyh_elementov
3. Основные этапы метода конечных элементов (МКЭ). [Электронный ресурс]. Режим доступа: https://infopedia.su/8xad70.html
4. Ушаков Д. М., Телерман В. В. Системы программирования в ограничениях (обзор) // Системная информатика: Сб. науч. тр. Новосибирск: Наука, 2000. Вып.7: Проблемы теории и методологии создания параллельных и распределенных систем. С. 275—310.
5. Нариньяни А.С. Недоопределенные модели и операции с недоопределенными значениями. – Новосибирск, 1982. – 33с.