Назад в библиотеку

Методы построения функций в специализированной оболочке для создания интеллектуальных САПР

Автор: Григорьев А.В.
Источник: Методы построения функций в специализированной оболочке для создания интеллектуальных САПР // Искусственный интеллект. – Донецк, 2001 – №3 – C. 40–53.

Аннотация

А.В. Григорьев. Методы построения функций в специализированной оболочке для создания интеллектуальных САПР. В статье разработан алгоритм обобщения, формирующий табличную модель функций базового блока, способную обеспечит использование ее в механизме логического вывода, построенного на основе недоопределенных обобщенных динамических вычислительных моделей Нариньяни. Задача создания модели функции решается путем обобщения значений свойств базовых блоков, которая сводится к созданию множества доменов значений свойств, а так же созданию И/ИЛИ-дерева методом обобщения по признакам.

Введение

Открытый, многоуровневый характер базы знаний (БЗ) интеллектуальной САПР делает необходимым использование для формального описания концептуальной модели (КМ) предметной области (ПрОб) САПР семиотической модели (СМ) [1]. СМ позволяет формально описать систему взаимосвязанных модельных уровней САПР (структурный, логический и т.д. [2]). Каждому уровню соответствует открытая БЗ о множестве возможных решений данного уровня.

В работе [3] предложена СМ БЗ САПР, ориентированная на решение типичных задач проектирования. Для представления знаний для САПР в [3] принят следующий подход. БЗ представляет собой И-ИЛИ-дерево с определенными отношениями (продукциями) над ИЛИ-узлами. Цель вывода в БЗ - обеспечение выбора требуемого прототипа по техническому заданию (ТЗ) как подмножеству значений ИЛИ-узлов. Суть работы [3] состоит в задании составляющей СМ - процедуры П4, дающей однозначный ответ на вопрос - является ли данный синтаксически корректный элемент семантически верным.

В работе [4] рассматривается семантика СМ БЗ САПР, уточняется форма представления модели объекта, определяется представление модели пространства и времени. Набор уровней КМ ПрОб для интеллектуальных САПР рассматривается как система взаимосвязанных знаний о действительности. В [4] предлагается система глобальных аксиом СМ предметной области. Система аксиом включает 6 обязательных уровней: 1) исходной модели; 2) задания времени 3) моделей пространств; 4) пространственных точек; 5) «простых» свойств 6) значений "простых" свойств или функций. Число подуровней названных уровней не фиксировано и определяется предметной областью и желаемым уровнем детальности представления модели. Глобальные аксиомы задаются как системы локальных аксиом обязательных уровней.

В работе [5] показано, что пространство может быть представлено как совокупность фиксированного числа пространственных координат (ПК), меняющих значения своих свойств в зависимости от контекста (в дальнейшем "пространственные точки" - ПТ).

КМ ПрОб, предложенная в [4], позволяет определять ряд моделей движения объектов в пространстве и времени. В наиболее сложном варианте рассматривается движение физических точек (ФТ) в пространстве с течением времени. Движение есть смена отдельными ФТ идентификаторов ПК. Число ФТ и ПК в различные моменты времени различно. Оно характеризуется изменением числа и состава связей между ПК и, соответственно, числа, состава и значений свойств ФТ. Отдельная ФТ определяется через набор системообразующих и факультативных [6] свойств, связанных с доменами своих возможных значений.

Независимо от выбранного типа движения состав пространств в данном прототипе и состав ПК и ФТ в отдельных пространствах может быть определен списком ПТ для выбранного подмножества пространств с указанием состояния границ ПТ.

Исходя из [4] в работе [5] предложена трактовка процедуры П4 для СМ БЗ САПР c предложенной семантикой. Процедура П4 в этом случае задает алгоритм управления движением в СМ пространства и времени. Основой данного алгоритма является потоковый алгоритм интерпретации недоопределенных обобщенных динамических вычислительных моделей (ОВМ) Нариньяни [7]. Т.о., главным требованиям к моделям функций является способность обеспечить указанный алгоритм интерпретации. Имеется два принципиально различных пути построения моделей функций:

- прямой экспертный ввод моделей функции в виде формулы, таблицы или графика;

- автоматическое создание моделей функций путем обучения по примерам.

Прямой ввод модели функции, например – в виде формулы, для базового структурного блока осуществляется в случае, если она известна пользователю. В случае, если функция неизвестна пользователю (ввиду низкой квалификации пользователя или отсутствия данных), то становится необходимым этап автоматического построения модели функций на основе обобщения ряда примеров.

Ранее в работе [8] автором был предложен аппарат построения системы формульных функций для базовых блоков, удовлетворяющий требованиям потокового алгоритма ОВМ Нариньяни.

Цель данной статьи состоит в описании методов построения табличной модели функций в СМ на основе обобщения ряда примеров. В качестве примеров при обобщении используются жизненные циклы некоторого объекта. Данная модель функции должна иметь форму, способную обеспечить использование ее в ОВМ. Предлагается строить модель табличной функции в форме модуля знаний, представленного в виде И/ИЛИ дерева с неявно определенными продукциями, связывающими возможные комбинации признаков в “или ” узлах. Конкретные задачи, решаемые в данной работе:

  1. показать особенности построения табличной модели функций в условиях семантики модели пространства-времени;
  2. описать особенности построения табличной функции в форме модуля базы знаний путем обучения на примерах;
  3. дать описание механизма интерпретации данной модели функций в процессе логического вывода в среде процедуры П4.

1. Особенности представления модели функций

Покажем особенности построения табличной модели функций в условиях семантики предлагаемой модели пространства-времени, а так же рассмотрим особенности СМ ПрОб, определяющие форму представления табличной функции в форме модуля базы знаний.

СМ есть открытая формальная система [1]: F = <T,C,A,П,r,b,g,d>, где T - множество базовых элементов системы; С - множество правил построения синтаксически правильных формул; A - множество аксиом F, подмножество формул из С, которым априорно присваивается статус истинности; П - множество правил вывода (семантические правила), позволяющие получать из A новые синтаксически правильные формулы, которым присваивается статус истинности; r, b, g, d - правила изменения для T, C, A и П. Требование конструктивности СМ предполагает реализацию следующих процедур: П1 - определения принадлежности данного элемента множеству Т; П2 - идентификации различия элементов множества Т; П3 - определения синтаксической корректности элементов, построенных посредством правил С. Процедуры П1, П2 и П3 должны быть конструктивными, т.е. завершаться через определенное число шагов. Конструктивная СМ является разрешимой, если существует конструктивная процедура П4, дающая однозначный ответ на вопрос - является ли данный синтаксически корректный элемент семантически верным.

1.1. Семантика модели пространства-времени

Особенности представления функций могут быть проиллюстрированы путем краткого рассмотрения семантики системы глобальных аксиом СМ ПрОб.

1.1.1 Уровень исходной модели. Исходная модель предмета уровня 1 включает блок с именем без внутренней структуры, имеющим единственное недоопределенное свойство без имени и структуры и единственную "круговую" связь, замыкающую блок сам на себя.

1.1.2 Уровень задания времени - блока и свойства. Этот уровень предполагает декомпозицию исходного свойства Nil1Д блока П на три подсвойства - обратный элемент, время T и неопределенность. Одновременно выполняется декомпозиция блока П на обратный элемент, блок Время (в дальнейшем просто "В") и неопределенность (рис. 1).

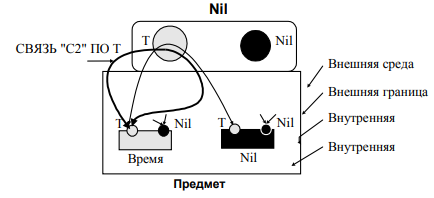
Рисунок 1 - Уровень ввода времени как свойства и блока

Рисунок 1 - Уровень ввода времени как свойства и блока

1.1.3 Уровень значений свойства времени и моделей пространств. Уровень предполагает декомпозицию свойства T на совокупность дискретных значений времени и одновременную декомпозиция блока В на совокупность моделей пространств, соответствующих отдельным значения времени (рис. 2).

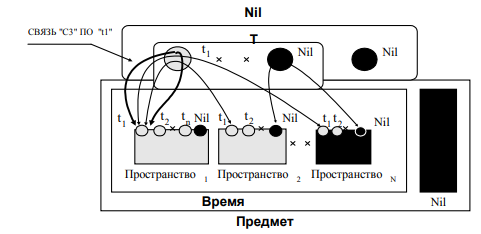
Рисунок 2 - Уровень определения моделей пространств

Рисунок 2 - Уровень определения моделей пространств

1.1.4 Уровень пространственных точек (ПТ) и их идентификаторов. Уровень предполагает перевод всех значений свойства T в разряд новых свойств и дальнейшую их декомпозицию на ряд собственных значений, в качестве которых выступают идентификаторы физических точек пространства. Одновременно выполняется декомпозиция моделей пространств P на блоки - физические точки (рис. 3).

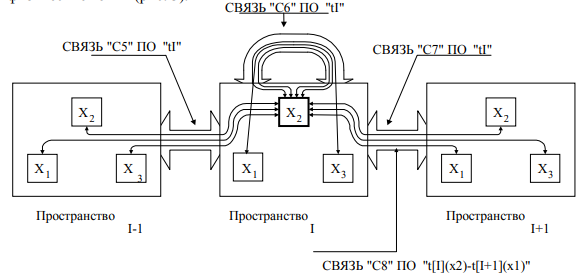
Рисунок 3 - Фрагмент совокупности связей ПТ

Рисунок 3 - Фрагмент совокупности связей ПТ

1.1.5 Уровень «простых» свойств и внутренних функций блоков. Уровень предполагает перевод всех идентификаторов пространственных координат из разряда значений в разряд новых свойств и дальнейшую их декомпозицию на ряд собственных значений - идентификаторов "простых" свойств физических точек пространства, а так же декомпозицию моделей блоков - физических точек пространств на множество блоков - носителей простых свойств или внутренних функций (ВФ). Каждое "простое" свойство есть потенциал ПТ в данной предметной области (гидро, тепло и т.д.). Совокупность свойств внешней границы отдельной ПТ определяется множеством ее связей (табл. 1).

Таблица 1 Пример состава свойств ПТ X20.

Таблица 1 - Пример состава свойств ПТ <b>X</b><sub>2</sub><sup>0</sup>.

В этом примере верхние индексы нумеруют свойства в пределах всего множества свойств данного уровня, а нижние индексы - в пределах вышележащей структуры данных.

1.1.6 Уровень значений "простых" свойств и "кортежей" функций. Выполняется перевод всех идентификаторов "простых" свойств ПТ из разряда значений в разряд новых свойств и дальнейшую их декомпозицию на ряд собственных значений, т.е. идентификаторов значений "простых" свойств, а так же декомпозиция ВФ на блоки - носители значений "простых" свойств - "кортежи". После выделения значений свойств, которое происходит на шестом уровне, может выполняться обобщение моделей-прототипов с целью формирования БЗ.

Методы построения функций в САПР, независимо от ориентации на предметные области, делятся на две группы - макро - и микрофункции [2]. Микрофункция – способ построения функциональных моделей объектов, при котором объект представлен моделью структуры, а модели функций задаются только для базовых блоков структурной иерархии. Функция модели объекта в целом строится как объединение базовых функций с помощью модели структуры. Макрофункция – способ построения функциональных моделей объектов, при котором объект не имеет модели структуры, а модель функции объекта задается без учета структуры объекта. Можно сказать, что модели функций базовых блоков в микрофункции построены как макрофункции.

Можно сделать вывод, что предложенная модель функции в данной СМ соответствует модели микрофункции, что отвечает требованиям САПР.

1.2. Состав основных элементов СМ. Опишем особенности СМ ПрОб, определяющие форму представления табличной функции в виде модуля базы знаний. В упрощенном виде множество основных элементов СМ имеет вид.

1.2.1 T - множество базовых элементов системы. Содержит в своем составе следующие элементы:

  1. Шкала времени прототипа Pk - упорядоченная последовательность идентификаторов моментов времени, связанных с пространствами Tk=&{Tjk}j=1Nk.
  2. "Полный" прототип есть траектория движения объекта во времени, заданная как совокупность состояний пространств в заданные моменты времени, принадлежащие шкале времени прототипа Pk. "Полный" прототип определяется как Pk=&{Пlk}l=1Nk и включает совокупность "частных" n-х прототипов Pnk=&{Пnlk}i=1n при n≤Nk и Pnk⊂Pk
  3. Шкала пространства Пlk - упорядоченная последовательность идентификаторов ПТ, связанных с пространствами Пi=&{Xij}j=1Ji.
  4. Шкала потенциала Eijk - упорядоченная последовательность потенциалов ПТ, связанных с пространствами Пi=&{Xij}j=1Ji.
  5. Граница ПТ Xijm содержит все потенциалы всех ПТ, связанных с данной ПТ "простыми" связями, а так же "собственный" потенциал данной ПТ.
  6. "Простая" связь между ПТ есть средство задания эквивалентных значений для двух потенциалов, принадлежащих разным границам.
  7. Пi=&{Xijm}j=1Ji - состояние пространства как совокупность Xijm - комбинаций состояний свойств-потенциалов на границе всех ПТ Xij.
  8. Текущее время Tj при 1≤j≤Nk.
  9. Достоверность прототипов Д(Pk)=100% [8].

1.2.2 А - множество семантически правильных формул. Множество А определяет содержимое БЗ. А является подмножеством С и совпадает с множеством семантически верных прототипов (имеющих прецеденты в практике). Различаются такие составляющие А:

  1. A1 : P = ∨{Pk}k=1K - множество семантически верных прототипов (см. выше глобальные и локальные аксиомы).
  2. A2 : обобщенный набор моделей пространств и обобщенная шкала значений времени для некоторого множества прототипов П = &{Пj}j=1N или T = &{Tj}j=1N
  3. A3 : обобщенная модель i-го пространства задается как Пi = ∨{Пij}j=1N, где Пij -возможное i-е состояние j-го пространства. Тогда Pk = &{Пijk}i=1N, где Пijk - требуемое состояние i-го пространства.
  4. A4 : обобщенный набор ПТ X = &{Xi}i=1Mi как объединение всех возможных ПТ всех пространств из всех прототипов.
  5. A5 : c каждой j-й ПТ i-го пространства Xij связано множество возможных комбинаций семантически верных состояний ее границ во всех прототипах - Xij = &or{Xijm}m=1M'ij, а так же - во всех пространствах и прототипах Xij = &or{Xijm}m=1M'ij

1.2.3 С - множество правил построения синтаксически правильных формул. Множество С совпадает с множеством синтаксически возможных прототипов P, заданным как декартово произведение всех возможных семантически верных состояний границ всех ПТ: P={Pt}t=1T=X1×..×XW.

1.2.4 . Трактовка процедур П1, П2 и П3 соответствует [3].

2. Метод построения моделей функций путем обобщения

Опишем особенности построения табличной функции для некоторого базового блока PijB в форме модуля базы знаний путем обучения на примерах. В качестве примера используем при обобщении жизненный цикл некоторого объекта Mk (рис. 4), состоящий из ряда пространств, или же ряд жизненных циклов { Mk }.

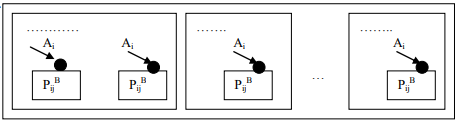
Рисунок 4 - Модель или жизненный цикл объекта

Рисунок 4 - Модель или жизненный цикл объекта

2.1 Формирование первоначального табличного вида модели функции. Первым шагом построения модели функции является собственно формирование таблицы значений для данной функции. Число функций определяется следующими соображениями. Каждый из вариантов комбинации свойств, входящих во внешнюю границу получает номер - номер прототипа. Каждый набор свойств внешней границы базового блока, т.е. прототип блока 5-го уровня представления Pi=(A1, A2,..), имеет собственную функцию как совокупность возможных комбинаций значений свойств (прототипов 6-го уровня). Тип Р={Pi} 5-го уровня задает класс функций, отличающихся набором свойств. Тип Р может быть представлен обобщенным набором свойств, часть из которых - системообразующие, т.е. обязательные, а остальные – факультативные, т.е. необязательные.

Тип P как совокупность свойств границы блока может быть обобщен в виде И/ИЛИ-дерева. В случае декомпозиции модели до уровня значений свойств может быть выполнено обобщение кортежей (см. выше) как функций базовых блоков. Каждый базовый блок – прототип Pi 5-го уровня в свою очередь рассматривается как тип 6-го уровня и представляется набором значений, привязанных к свойствам внешней границы блока. Данный набор значений и является единицей функции. Собственно функция может быть представлена в виде таблицы:

Таблица 2. Таблица функций

Таблица 2. Таблица функций

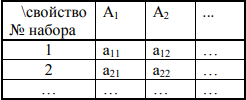
Каждая новая строка в таблице функций – это оригинальный набор значений для заданного набора свойств (отличается хотя бы одним значением свойства). Источник появления свойств в таблице функций – это различные контексты в модели, где встречается данный тип базового блока, имеющий в качестве структуры входов-выходов данный номер прототипа Pi.

При выполнении декомпозиции свойств на значения отдельный прототип Pi как совокупность свойств внешней границы базового блока превращается либо в обобщенный тип базовой функции PiB, либо в ряд типов, объединенных по «ИЛИ» {PijB}. Каждый новый тип есть совокупность оригинальных (уникальных) комбинаций значений свойств границы блока (строк). Каждая оригинальная комбинация нумеруется в пределах своего типа PijB (или PiB)

Каждая табличная функция получает две формы представления:

  • И/ИЛИ-дерево для множества строк в таблице;
  • совокупность доменов, задающих множество возможных значений для всех свойств границы.

Наличие двух форм представления обеспечивает высокую гибкость и эффективность использования функции на практике как в процессе задания параметров модели объекта, так и в процессе моделирования объекта. Повышение эффективности интерпретации функции предполагает:

  • сокращение числа операций с таблицей в ходе интерпретации табличной функции;
  • повышение удобства работы пользователя в процессе задания значений требуемых ему параметров.

Рассмотрим структуру и порядок взаимодействия указанных форм представления функции.

2.2 Формирование И/ИЛИ-дерева. Каждая совокупность строк значений представляется в виде И/ИЛИ-дерева. Представление функции в виде И/ИЛИ-дерева имеет два этапа:

  1. упорядочивание столбцов и строк в таблице;
  2. собственно построение И/ИЛИ-дерева.

Все свойства относятся к ряду массивов и типов свойств; это явно указывается в структуре идентификатора свойства Ai.

2.2.1 Упорядочивание таблицы. Все строки и столбцы в таблице функций перед обобщением могут быть сгруппированы следующим образом:

  1. Упорядочивание по столбцам. Упорядочивание производится по типам и массивам свойств следующим образом:
    • Определяется шкала над элементами массива свойств. Все элементы одного массива данных смежны по номерам.
    • Массивы (или единичные свойства) одного типа данных смежны по номеру. Порядок вводится своей отдельной шкалой.
    • Определяется шкала над типами свойств: Т1, Т1,…,Тn, где Тi – отдельно взятый тип. Порядок вводится своей шкалой.
  2. Упорядочивание строк. Упорядочивание производится по размеру множеств значений и их повторяемости. Цель такого упорядочивания – расставить строки в таком порядке, чтобы: а) отдельные значения в различных свойствах располагались только по порядку их старшинства, сверху вниз; б) вес значений в различных свойствах зависел от положения свойства во множестве свойств (справа налево), от младших к старшим. Т.е., фактически формируется позиционная система исчисления, имеющая разные веса отдельных позиций. Итог такого упорядочивания состоит в формировании базового первоначального порядка нумерации строк в таблице. На рисунке 5 показан этап упорядочивания множества строк в табличной модели функции, выполненный по значениям свойства Aj и Aj-1.
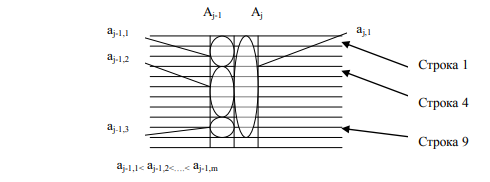
Рисунок 5 - Упорядочивание строк по значениям свойств A<sub>j</sub> и A<sub>j-1</sub>

Рисунок 5 - Упорядочивание строк по значениям свойств Aj и Aj-1

2.2.2 Собственно построение И/ИЛИ-дерева. После упорядочивания таблицы формируется И/ИЛИ-дерево, где каждый ИЛИ-синтерм (узел) связывается с подмножеством номеров возможных прототипов, что в данном случае обозначает подмножество номеров строк к исходной табличной функции. Можно сказать, что процесс построения И/ИЛИ-дерева в упрощенном виде повторяет процесс формирования И/ИЛИ-дерева из работы [9]. Суть данной работы состоит в построениии И/ИЛИ-дерева по схемам выделения общих и отличных частей описаний прототипов [6], предназначенным для обобщения моделей структур.

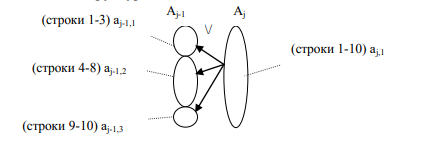
Рисунок 6 – И/ИЛИ-дерево, эквивалентное упорядоченному фрагменту строк таблицы на рис. 5

Рисунок 6 – И/ИЛИ-дерево, эквивалентное упорядоченному фрагменту строк таблицы на рис. 5

2.3 Формирование доменов значений свойств. На основе упорядоченного множества строк в таблице, т.е. фактически на базе И/ИЛИ-дерева выполняется формирование доменов значений свойств. Вид доменов зависит от полноты таблиц, т.е. от степени обобщения предварительного обобщения контекстов. Каждый вход-выход Ai представлен доменом своих значений: Ai={aij}j. Домен может быть получен путем обобщения в различных контекстах и в различной степени общности. Каждая функция (тип) подвергается следующим этапам обобщения:

  1. По каждому отдельному свойству данной функции (имеющей конкретный идентификатор) определяется список возможных его значений. Т.о. формируется домен (в терминах теории ОВМ) возможных значений данного входа-выхода Аi функции PijB в пределах всех возможных контекстов использования данной функции данного типа, данного массива, данного номера, данного отца (вышележащий блок), но в пределах разных жизненных циклов (моделей объектов), т.е. имеющей конкретное место в модели. На выходе данного процесса обобщения получим домен DpT.
  2. Для всех свойств одного типа T1 формируется набор значений как обобщение в пределах функции PijB, затем PiB и т.д. по всем имеющимся базовым функциям, где встречается данный тип свойства (в любом месте, с любым именем массива, с любым номером в массиве, в любой модели объекта). Т.о., для каждого входа-выхода Аi некоторого прототипа функции PijB получаем домен DpT его возможных значений, исходя из принадлежности его к некоторому типу свойств.

Наличие двух таких доменов позволяет либо строить новые модели, используя определенный таким образом тип свойств, либо выполнять процесс интерпретации функций, исходя из возможных контекстов использования отдельных значений свойств. Рассмотрим последнюю возможность.

2.4. Формирование внутреннего механизма интерпретации функции для взаимного отображения доменов друг в друга. Дадим описание механизма интерпретации данной модели функций в процессе логического вывода в среде процедуры П4. Сужение домена осуществляется либо:

  • пользователем напрямую в ходе диалога задания требуемых значений параметра;
  • косвенно - посредством интерпретации отношений эквивалентности двух доменов, т.е. структурных связей в СМ ПрОб.

Как в том, так и в другом случае процесс сужения доменов функции протекает аналогично. Порядок сужения множеств доменов {Ai}i∀, i≠j при изменении множества возможных значений некоторого домена Aj:

Aj→A'j, A'j⊂Aj

показан на рис 7.

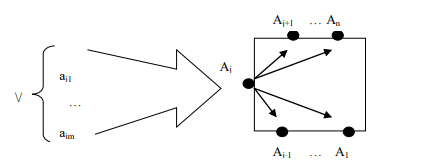
Рисунок 7 – - Порядок "сужения" множества доменов значений свойств функции при изменении одного из доменов

Рисунок 7 – - Порядок "сужения" множества доменов значений свойств функции при изменении одного из доменов

Данный процесс соответствует «удалению» из таблицы функций тех строк, где имеются значения домена Aj, входящие в Ajвыброс, а так же ряда строк, существование которых становится невозможно, исходя из факта, что контекст, в которых они были определены ранее, фактически становится невозможным.

Основой данного механизма является наличие неявных продукций, связывающих различные «или»-узлы И/ИЛИ-дерева и построенных на принадлежности признаков-значений к тем или иным прототипам. Удаление всех значений в домене, связанных с некоторым прототипом приводит к сужению возможных контекстов-прототипов у значений в других доменах. Такое сужение выполняется в соответствии с правилами вывода, заданными в [3]. Значения, список прототипов которых оказывается пуст, удаляются. Такой процесс может быть условно назван «вторичным сужением» доменов.

Процесс задания параметров базовых блоков пользователем может проводиться следующими путями:

  1. Посредством задания интервалов значений для ряда разрозненных параметров у различных базовых блоков. В этом случае модель базовых блоков представляется как совокупность доменов. Механизм И/ИЛИ-дерева как способ представления функций играет вспомогательную роль и используется для обеспечения процесса «вторичного сужения» доменов. Оптимизация процесса вывода в этом случае не возможна.
  2. Посредством задания значений всех параметров базового блока как совокупности цепочек значений. В этом случае модель функции базовых блоков представляется как И/ИЛИ-дерево. Механизм доменов как способ представления функций играет вспомогательную роль и используется для обеспечения процесса косвенного сужения доменов посредством интерпретации структурных связей в СМ ПрОб. В этом случае процесс ввода заданного набора параметров базового блока может проводиться под управлением критерия оптимизации из работы [3]. Данный критерий минимизирует число и сложность вопросов, обращаемых к пользователю в диалоге задания признаков модели при ее синтезе на основе базы знаний. Для модели табличной функции, представленной как И/ИЛИ-дерево, данный критерий оптимизации требует упорядочивания «или»-узлов И/ИЛИ-дерева в порядке уменьшения максимально - ожидаемого размера «вторичного сужения» оставшихся «или»- узлов. После выбора первого параметра происходит переупорядочивание «или»- узлов и процесс повторяется.
  3. Посредством задания набора параметров базовых блоков в порядке, оптимальном с точки зрения быстроты ввода множества параметров и интерпретации модели. В этом случае может проводиться процесс переупорядочивание свойств функции для целей оптимизации процесса диалогового задания параметров под управлением того же критерия из [3]. Для модели табличной функции, представленной как совокупность доменов, данный критерий оптимизации фактически требует упорядочивания свойств границы в порядке возрастания мощности доменов их возможных значений: |D1|<|D2|<...<|Dn|. Такое упорядочивание позволяет после задания на первом шаге свойства с минимальным размером домена максимально сузить размер табличной функции за счет процесса «вторичного сужения». После первого шага домены переупорядочиваются заново, исходя из новых размеров доменов, затем выполняется шаг 2 и т.д.

3. Практическое использование предлагаемого подхода

Данный подход использовался на практике как средство представления экономических функций в ходе построения системы автоматизации построения бизнес-планов. Существующие системы для разработки бизнес-планов, как правило, закрыты, в них нельзя ввести новые знания, алгоритмы, системы расчетов, невозможно изменить диалог с пользователем, они не позволяют гибко менять состав входных и выходных параметров проекта, задать интервал вместо конкретного значения параметра. В экономике существенную роль играют табличные функции. Можно выделить следующие важнейшие методы представления функций: а) собственно табличные функции; обычно содержат статистическую информацию, накопленную опытным путем; б) функции, заданные графиком; обычно сводятся к табличным; в) простые функции, содержащие простые математические операции; таковыми являются модели маркетинга, менеджмента, бухгалтерского учета; такие функции, во общем случае, могут быть сведены к табличным.

Наряду с моделью формульной функции в [8] предлагаемый подход к построению модели табличной функций в базе знаний как основы системы разработки бизнес-планов дает ряд ощутимых преимуществ и новых возможностей. Эти возможности и преимущества позволяют устранить некоторые недостатки аналогичных продуктов. Помимо общих возможностей (ввод новых знаний, алгоритмов, систем расчетов, адаптации диалога к пользователю), свойственных данному подходу вообще, становится возможным:

  • вводить в качестве входных данных проекта любых свойств в модели и любых требуемых данных – в качестве выходных;
  • работать при задании входных параметров и при анализе выходных параметров с интервалами возможных значений; при этом могут рассматриваться интервалы «не определено», «множество пусто» и т.д.

Такие возможности позволяют проводить более эффективно анализ чувствительности проектов, выбирать начальные данные проекта, необходимые для достижения желаемых результатов и т.п. На практике для построения модели ПрОб была использована функция NPV, являющаяся основным показателем бизнес-плана.

Выводы

В статье разработан алгоритм обобщения, формирующий табличную модель функций базового блока, способную обеспечит использование ее в механизме логического вывода, построенного на основе недоопределенных обобщенных динамических вычислительных моделей Нариньяни. Задача создания модели функции решается путем обобщения значений свойств базовых блоков, которая сводится к созданию множества доменов значений свойств, а так же к созданию И/ИЛИ-дерева методом обобщения по признакам.

Показано, что совокупность методов, применяемых для построения базы знаний для структурной компоненты модели, могут с незначительными дополнениями или упрощениями использоваться и для построения базы знаний о табличных функциях. Показана целесообразность применения данного подхода в экономике. Предложенный подход к решению задачи является достаточно простым, а при реализации сводится к выборке из таблиц и сортировке.

Список использованной литературы

1.Поспелов Д.А. Ситуационное управление: теория и практика. М.: Наука, 1986.-288 с.
2. Норенков И.П. Введение в автоматизированное проектирование технических устройств и систем. М.: Высш. шк., 1986. - 304 с.
3. Григорьев А.В. Семиотическая модель базы знаний САПР. Научные труды Донецкого государственного технического университета Серия: Проблемы моделирования и автоматизации проектирования динамических систем, выпуск 10: - Донецк, ДонГТУ, 1999. - С. 30-37.
4. Григорьев А.В. Комплекс моделей САПР как система взаимосвязанных уровней знаний о действительности. В кн. Информатика, кибернетика и вычислительная техника (ИКВТ-2000). Сборник трудов ДонГТУ, Выпуск 15. Донецк: ДонГТУ, 2000. - С. 155-167.
5. Григорьев А.В. Построение процедуры П4 для семиотической модели пространства-времени. В кн. Труды межд. н.-п. конф. KDS-2001. Том 1. Санкт-Петербург, 2001. - С. 169-177.
6. Зубенко Ю.Д. Системный анализ. Донецк: ДонГТУ, 1995. - 166 с.
7. Нариньяни А.С. Недоопределенность в системах представления и обработки знаний. // Известия АН СССР. Техническая кибернетика. - 1986.- № 5. - С. 3-28.
8. Григорьев А.В., Бондаренко А.В., Шойхеденко А.В. Интерфейс табличного процессора EXCEL и специализированной оболочки для синтеза интеллектуальных САПР и АСНИ. В кн. Информатика, кибернетика и вычислительная техника (ИКВТ-97). Сборник трудов ДонГТУ, Выпуск 1. Донецк: ДонГТУ, 1997. - С. 229-238.
9. Григорьев А.В., Каспаров А.А. Обобщение знаний в интеллектуальной системе с семиотической моделью представления знаний. Научные труды Донецкого государственного технического университета Серия: Проблемы моделирования и автоматизации проектирования динамических систем, выпуск 29: - Севастополь: «Вебер», 2001. – С. 106-113.