Аннотация
Григорьев А.В. Решение дифференциальных уравнений в интеллектуальных САПР методом программирования в ограничениях. В работе освещены принципы решения дифференциальных уравнений в инструментальной оболочке для построения интеллектуальной САПР на основе технологии программирования в ограничениях. По известным примерам объяснена суть подхода. Предлагаемый подход позволяет по-новому рассмативать задачи решения дифференциальных уравнений. Основным результатом работы является повышение гибкости и эффективности программных средств решения дифференциальных уравнений.
1. Введение, постановка задачи
Программирование в ограничениях (ПрОг) как теория решения численных задач начиналась как раздел искусственного интеллекта («вычислительные недоопределенные модели») и являлась развитием метода обобщенных вычислительных моделей [1]. В настоящее время - это самостоятельная технология, претендующая на роль универсального высокоэффективного средства решения разнообразных задач – вычислительных, комбинаторных, теоретико-множественных. Основой технологии является представление алгоритма как совокупности объектов (переменных), имеющих множество значений (интервалов или множеств) и ограничений (функций). Суть технологии состоит во взаимной «утряске» множеств значений переменных с использованием набора функций, обеспечивающих произвольное направление расчетов. Доказывается, что этот процесс – конечный во времени и предлагается конкретный алгоритм «утряски» - «потоковый алгоритм» [1]. Ссылаясь на [2] можно указать, что ПрОг особенно полезно там, где кончаются возможности обычной математики. Оно используется при решении задач планирования, проектирования, прогнозирования, в инженерных и экономических расчетах, при создании графических интерфейсов, в системах понимания естественного языка и др. Можно назвать такие наиболее известные зарубежные системы, реализующих парадигму программирования в ограничениях: Prolog III [3], CLP(R) [4], CLP(BNR) [5], clp(FD) [6], CHIP [7], ILOG Solver [8], Newton [9] и др. Однако в числе задач, решаемых с позиций ПрОг, отсутствуют задачи численного решения дифференциальных уравнений (ДУ). Численное решение решения ДУ с позиций ПрОг позволило бы рассматривать задачу решения ДУ в новой постановке. Например: 1) рассматривать не только граничные условия задачи, а так же условия, задаваемые для любой подобласти области определения; 2) рассматривать не только начальные условия задачи, а условия, задаваемые для любых промежуточных или конечных состояний; 3) рассматривать задачи проверки существования решения для данного набора значений параметров; 4) получать неоднозначные решения; 5) решать любые обратные задачи, например задачу поиска начальных или граничных условий по виду возможного решения и т.д. Таким образом, существенно может повыситься гибкость и эффективность средств решения ДУ. Это делает решение названной задачи актуальной. Наиболее актуальной она является для САПР, где решение ДУ необходимо по определению. Применение подобного подхода в инструментальной оболочке для построения интеллектуальных САПР позволит автоматизировать процесс решения ДУ для любых предметных областей на основе интеллектуального же метода решения. Целью данной статьи является освещение общих принципов решения ДУ в инструментальной оболочке для построения интеллектуальных САПР на основе ПрОг, а так иллюстрация метода решения на примерах.
2. Общая формулировка и область применения и подхода
Если трактовать технологию ПрОг с точки зрения физической семантики предметной области, которая является основой представления моделей в САПР, то речь идет о ряде потенциалов (т.е. объектов), связанных функциями – отношениями между потенциалами, характер которых зависит от свойств среды, разделяющей потенциалы. Такие отношения, в зависимости от уровня представления моделей в САПР [10,11,12], могут иметь характер алгебраических или булевых уравнений (уровень функционально-логической модели), простых ДУ (макромодель количественного уровня) или уравнений в частных производных (микромодель количественного уровня). При этом важно отметить, что данное деление моделей в САПР не зависит от конкретной предметной области. Например, на уровне количественной макромодели в предметной области электротехника функции могут иметь вид уравнений сопротивления (алгебраическое уравнение), индуктивности, емкости (простые ДУ) и т.п. Решение алгебраических или булевых уравнений не представляет принципиальной трудности для применения метода ПрОг, однако же, решение ДУ с помощью данного метода – это не тривиальная задача. Во-первых, следует определить те методы решения ДУ, которые в принципе возможно использовать как полигон для применения ПрОг, и, вовторых, выполнить конкретное представление ДУ способом, при котором возможно применение ПрОг. Таким образом, задача применения ПрОг для решения ДУ в САПР распадается на такие подзадачи: 1) обязательная интерпретация ДУ с точки зрения физической семантики предметной области; 2) представление методов численного решения ДУ, ориентированных на физическую семантику предметной области, в форме, требуемой с точки зрения применения технологии ПрОг. Мы не будем накладывать ограничений на класс решаемых ДУ, предполагая, однако, за ними физическую семантику ПрОб. Как главную проблему мы будем рассматривать представление методов численного решения ДУ, ориентированных на физическую семантику предметной области. Т.о., не все методы решения ДУ подходят под эту задачу. Интерес для нас представляют методы, где явно или неявно просматривается физическая семантика предметной области. Здесь можно назвать метод конечных разностей, метод конечных элементов, метод прогонки [13,14] и т.д. Соответственно, нас не интересует метод коллокации, наименьших квадратов, Галеркина и т.п.
3. Концептуальная модель предметной области как основа для решения ДУ методом ПрОг
Интерпретацию ДУ с точки зрения физической семантики предметной области [15] предлагается выполнять с помощью унифицированной концептуальной модели предметной области (УКМ ПрОб), разработанной автором ранее для представления моделей в интеллектуальных САПР [16]. Данная УКМ ПрОб построена с целью: 1) представления моделей объекта на основе физической семантики предметной области; 2) создания системы взаимосвязанных уровней представления моделей [17]. Модель использует объектноориентированное представление физической модели мира и включает в себя как отдельные элементы время, пространство, физические точки (ФТ), потенциалы и т.д. Система уровней модели объекта строится путем последовательной декомпозиции неопределенностей, рассматриваемых как явные характеристики элементов ПрОб. В соответствии с классификацией Нариньяни А.С. рассматриваются [18] все три типа неопределенности, т.е. грубости, неполноты и альтернативности [1]. Предлагаемая УКМ ПрОб строилась исходя из возможности дискретного описания любой ПрОб, любого класса зависимостей, пространственного размера объекта проектирования и временных границ. Представление некоторого избранного метода решения ДУ в рамках данной УКМ ПрОб обеспечивается за счет построения желаемой модели пространства и времени на соответствующем уровне декомпозиции модели. Конкретно это выглядит следующим образом:
- По модели пространства выполняется определение:
- числа пространственных измерений;
- метрики пространства;
- числа пространственных ФТ и их координат;
- состава типов возможных потенциалов ФТ;
- состава «собственных» потенциалов ФТ;
- «допусков» (ограничений, но не в смысле ПрОг) на базе метрики, цель которых разрешить возникновение связей по потенциалам между ФТ для задания факта влияния потенциалов одних ФТ на потенциалы других ФТ, но только на некотором уровне близости ФТ друг от друга; «допуски» различны для различных типов потенциалов;
- состава «чужих» потенциалов на внешних границах ФТ, как следствие возникновения связей между ФТ;
- внутренних функций для ФТ, обеспечивающих зависимость «собственных» потенциалов ФТ от потенциалов «чужих» ФТ, лежащих на границе ФТ; число внутренних функций – не меньше числа «собственных» потенциалов ФТ, но и не больше произведения числа «своих» потенциалов на число «чужих»;
- По модели времени выполняется определение:
- числа пространственных временных точек (ВТ) и их координат;
- определение метрики времени и т.д.
4. Иллюстрация метода решения ДУ на примере
Рассмотрим, для примера, представление в рамках данной УКМ ПрОб метода конечных разностей, применяемого для решения следующего известного ДУ, рассмотренного ранее в [14]:
y''+p(x)*y'+q(x)*y=f(x),
при x ∈ [a,b] и следующих граничных условиях:
α0*y(a)+α1*y'(a)=A;
β0*y(bβ1*y'(b)=B.
После деления интервала [a,b] на n равных частей, размером h и замены производных конечными разностями, а функций – дискретными значениями получается:
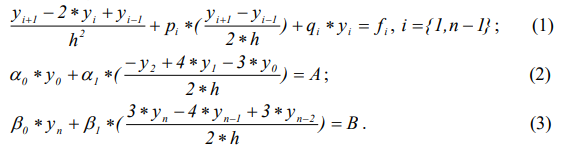
Данная система уравнений может быть решена для поиска y(х) по однозначно заданным α0,α1,A,B, а так же β0,β1, p(x), q(x), f(x). Представим метод решения этой системы, исходя из вышеописанного подхода. Число ФТ у нас n+1. Любые входные данные, если мы хотим их изменять, рассматриваются нами как потенциалы. Например, собственные потенциалы ФТ включают искомое значение Yi, вспомогательные функции fi,gi и потенциалы граничных точек, отражающих влияние внешней среды - A (или B). Собственные потенциалы задаются рефлексивными (круговыми) связями, а чужие потенциалы передаются на внешние границу ФТ от ФТ - соседей, достаточно близких к данной ФТ, чтобы возникла связь по данному типу потенциала. «Допуски» по метрике для потенциалов fi,gi, A (или B) выбираются такими, что связи не возникают при данных координатах ФТ (<h ,при данных координатах ФТ, т.е. шаге h по X). «Допуски» для потенциалов типа Yi выбирается таким, что связи возникают между данной ФТ и двумя ее соседями справа по оси X, а так же двумя соседями слева по оси X, т.е. допуск имеет вид ≤2h. Наличие связей с двумя соседями слева и справа – это максимально возможное число связей для представления собственно ДУ (по одному соседу) и граничных условий (по два соседа). Предполагается, что внутренние функции ФТ используют столько потенциалов, сколько необходимо, но из числа уже существующих. Представление части совокупности связей между внутренней точкой и ее соседями показано на рис. 1, и на рис. 2 – представление совокупности связей между граничной «n»-й точкой и ее соседями.
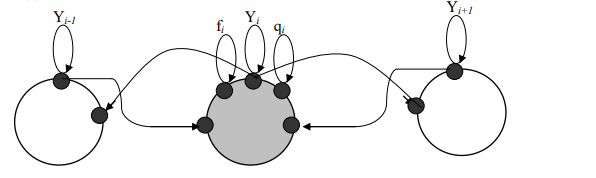
Рисунок 1 - Фрагмент схемы представления внутренних точек
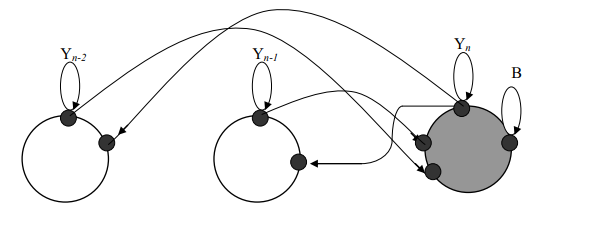
Рисунок 2 – Представление граничных точек
Такое представление ФТ сразу разделяет потенциалы ФТ как параметры внутренних функций на входные и выходные, предопределяя тем самым вид «функций – ограничений» для ПрОг. В данном случае этих функций становится ровно столько, столько имеется собственных потенциалов у ФТ. Каждая «функция – ограничение» задает влияние на свой конкретный потенциал «чужих» потенциалов и прочих своих. Данного количества «функций – ограничений» как раз достаточно, что бы отследить изменение любого потенциала и выявить его влияние на другие потенциалы. Таким образом, уравнения 1-3 должны быть заменены совокупностью функций, имеющих вид:
Пi=F(П1,...,Пi-1,Пi+1,...,Пk,K1,...,Km).
Тут: Пi – потенциалы ФТ, числом k; Ki – внутренние коэффициенты уравнений, числом m. При наличии большого числа потенциалов у ФТ с целью уменьшить трудоемкость формирования множества «функцийограничений» может быть предложен другой подход. Ранее в работе [19] автором был предложен метод динамического формирования необходимых для перерасчета той или иной требуемой переменной конкретных «функций-ограничений», исходя из следующего первоначально задаваемого базового представления совокупности ограничений: F(x0,...,xn)=0.
Для применения данного подхода может быть дана, например, следующая форма записи системы уравнений:
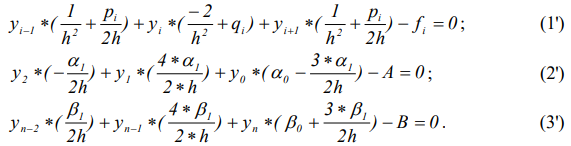
Данная форма записи исходит из того, что потенциалами являются только yi, а все прочие – являются внутренними коэффициентами. Тут уравнение (1') задает зависимость для внутренних точек, а уравнения (2'-3') - представление зависимости для граничных точек. Исходя из данной системы внутренняя функция влияния «чужих» потенциалов на «свой» потенциал ynдля «n»-й граничной точки будет иметь вид:
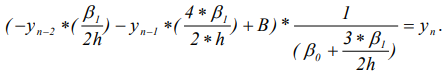
Для внутренней «i»-й точки уравнение влияния будет иметь вид:
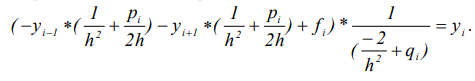
Полная система подобных внутренних функций обеспечит применение метода ПрОг. При автоматическом построении дискретных функций путем обобщения ряда жизненных циклов для представления «функций-ограничений» может применяться модуль знаний в виде И-ИЛИдерева с определенным над ним продукциями [20]. В этом случае для ФТ имеет место только одна обобщенная «функция-ограничение». Работа с совокупностью таких функций для выбора следующей «работающей» функции может выполняться на основе критерия «максимального сужения неопределенностей» [21], альтернативного в данном случае потоковому алгоритму Нариньяни А.С. Далее для всех потенциалов всех ФТ задаются возможные множества значений (однозначное значение, множество возможных дискретных значений, интервал, мультиинтервал, полная неопределенность). Теперь данная система уравнений может быть решена с целью поиска y(х) по неоднозначно заданным коэффициентам α0,α1,β0,β1, неоднозначным граничным условиям A,B, а так же неоднозначным значениям функций p(x), q(x), f(x). Кроме того, для любой ФТ может быть также введено обычно трактуемое ограничение на значение y(х). Может быть решена любая обратная задача, например, поиск значений коэффициентов α0,α1,β0,β1 по значениям y(х), поиск значений функций p(x), q(x), f(x) и т.п. В случае получения на выходе для одного из потенциалов пустого множества значений можно будет сделать вывод об отсутствии решения ДУ. В случае получения на выходе неоднозначного значения можно сделать вывод о существовании множества решений.
Выводы
В данной работе освещены общие принципы решения ДУ в инструментальной оболочке для построения интеллектуальных САПР на основе ПрОг и выполнена иллюстрация данного метода решения ДУ на известных примерах. Основой подхода являются результаты, полученные автором ранее: 1) УКМ ПрОб; 2) метод динамического формирования необходимых функций-ограничений для ПрОг. Предлагаемый подход к численному решению ДУ позволяет рассматривать задачу решения ДУ в новой постановке, что позволяет существенно повысить гибкость и эффективность средств решения ДУ. Особо следует отметить, что данная статья заканчивает цикл публикаций по адаптации всех результатов Нариньяни А.С. к задаче создания инструментальной оболочки для построения интеллектуальных САПР. Предлагаемая статья является так же основой для выполнения следующих работ: 1) программной реализации данного подхода в инструментальной оболочке для построения интеллектуальных САПР; 2) получения конкретных численных оценок эффективности данного подхода в сравнении с известными методами.
Список использованной литературы
1.Нариньяни А.С. Недоопределенность в системах представления и
обработки знаний // Изв. АН СССР. Техн. кибернетика, 1986. № 5. – С. 3 –
28.
2. А.С.Нариньяни, В.В. Телерман, Д.М. Ушаков, И.Е. Швецов
Программирование в ограничениях и недоопределенные модели. //
Информационные технологии. 1998. - № 7. – С. 12-20.
3. Colmerauer A. An introduction to Prolog III. Communications of the
ACM, 33(7), July 1990. – P. 69 – 90.
4. Jaffar J., Michayov S., Stuckey P., Yap R. The CLP(R) language and
system. ACM Transactions on Programming Languages and Systems, 14(3),
July 1992. – P. 339 – 395.
5. Benhamou F., Older W.J. Applying Interval Arithmetic to Real, Integer
and Boolean Constraints. Journal of Logic Programming, 1996.
6. Diaz D., Codognet P. A minimal extension of the WAM for clp(FD).
Proceedings of the 10th International Conference on Logic Programming, 1994.
7. Van Hentenryck P. Constraint Satisfaction in Logic Programming.
Logic Programming Series. MIT Press, Cambridge, MA, 1989.
8. Puget J.-F. A C++ Implementation of CLP. Tech. Report, Ilog, January
1994.
9. Benhamou F., McAllester D., Van Hentenryck P. CLP(Intervals)
Revisited. Proceedings of ILPS’94, Ithaca, NY, 1994. – P. 124 – 138.
10. Петренко А.И., Семенков О.И. Основы построения систем
автоматизированного проектирования. - К.: ВШ, 1984. - 296 с.
11. Норенков И.П. Введение в автоматизированное проектирование
технических устройств и систем. М.: Высш. шк., 1986. - 304 с.
12. Норенков И.П. Разработка систем автоматизации проектирования.
М.: МГТУ им. Э.Н. Баумана, 1994. – 207 с.
13. Пирумов И.Г. Численные методы. - М.: Изд-во МАИ, 1998. - 188
с.
14. Самарский А.А., Николаев Е.С. Методы сеточных уравнений.
Методы решения сеточных уравнений. М.: Наука, 1978. - 592 с.
15. Григорьев А.В. Семантика модели предметной области для
интеллектуальных САПР. Научные труды Донецкого государственного
университета. Серия "Информатика, кибернетика и вычислительная
техника", (ИКВТ-2000) выпуск 10. - Донецк, ДонГТУ, 2000. - С. 148-154.
16. Григорьев А.В. Унифицированная концептуальная модель
предметной области. Информатика, кибернетика и вычислительная техника
Сборник трудов ДонГТУ, Выпуск 1. Донецк: ДонГТУ, 1997. - С. 225-28.
17. Григорьев А.В. Комплекс моделей САПР как система
взаимосвязанных уровней о действительности. Научные труды Донецкого
государственного университета. Серия "Информатика, кибернетика и вычислительная техника", (ИКВТ-2000) выпуск 10. - Донецк, ДонГТУ,
2000. - С. 155-167.
18. Григорьев А.В. Представление недоопределенности знаний в
инструментальной оболочке для построения САПР. Искусственный
интеллект. N 1, 1999 , C. 96-106.
19. Григорьев А.В., Бондаренко А.В., Шойхеденко А.В. Интерфейс
табличного процессора EXCEL и специализированной оболочки для
синтеза интеллектуальных САПР и АСНИ. В кн. Информатика,
кибернетика и вычислительная техника (ИКВТ-97). Сборник трудов
ДонГТУ, Выпуск 1. Донецк: ДонГТУ, 1997. С. 229-238.
20. А.В. Григорьев. Методы построения функций в
специализированной оболочке для создания интеллектуальных САПР.
Искусственный интеллект. N 3, 2001, C. 40-53.
21. Григорьев А.В. Семиотическая модель базы знаний САПР.
Научные труды Донецкого государственного университета. Серия
"Проблемы моделирования и автоматизации проектирования динамических
систем". Выпуск 10: - Донецк: ДонГТУ, 1999. - С. 30-37.