Аннотация
Роговец Е.А., Григорьев А.В. Эффективность применяемого алгоритма построения моделей с ограничениями в различных САПР. В работе предлагается решение задачи параметризации, использован вариативный метод создания параметрической модели. Приведен обзор используемого процесса создания моделей. К ознакомлению представлен математический метод построения моделей. Данная работа нацелена на исследование современных технологий и методов решения задачи параметризации, а также освящение современных программных продуктов, реализующих эти технологии.
Введение
Зачастую, при проектировании, в чертёж приходится вносить изменения, вызванные недостатками конструкции или модификации, и порой даже незначительные корректировки в размерах одной детали приводят к редактированию значительной части чертежа. Различные САПР предлагают для использования огромное множество зависимостей и алгоритмов, основными являются два вида налагаемых зависимостей: геометрические и размерные. Углубление в изучение параметризации позволит более гибко настраивать модели, а также автоматизировать процесс построения объектов в системе.
Общая постановка проблемы
Параметрические операции — это ключевые методы построения геометрических фигур в процессе их моделирования. Основным элементом для большинства операций есть 3D-профиль, при движении которого осуществляется формообразование. Параметрическое моделирование существенно отличается от обычного двухмерного черчения или трехмерного моделирования. Конструктор, в случае параметрического проектирования, создает математическую модель объектов с параметрами, при изменении которых происходят изменения конфигурации детали, взаимные перемещения деталей в сборке и т.п. Таким образом, параметризация предполагает автоматическое построение и последующее решение соответствующей системы уравнений, обеспечивающих перерасчет подмножества параметров модели объекта по части параметров, изменивших свое значение. Подробная схема актуальности использования параметризации для модели обусловлено также и частыми изменениями параметров объекта, это показано на рис. 1. Т.о., типичная задача параметризации состоит в модификации, реконструкции полученного ранее решения. Специфика конкретных задач параметризации зависит от специфики предметной области и типа задачи: создание нового объекта, модификация известного решения. Разработка средств параметризации для специфических условий применения в той или иной проблемно-ориентированной САПР – это важная и актуальная задача.[1]
Классификация САПР
Существует классификация САПР, различающаяся полнотой систем: тяжелые, легкие и средние САПР:
Тяжелые. Основная особенность этого типа состоит в том, что их большие функциональные возможности, высокая производительность и стабильность получены в результате длительного развития. Все они довольно стары: CATIA появилась в 1981 г., Pro/Engineer — в 1988-м, Unigraphics NX, вышла совсем недавно, является результатом слияния двух весьма важных систем — Unigraphics и I-Deas, приобретенных вместе с компаниями Unigraphics и SDRC. Несмотря на то что такие системы значительно дороже других типов систем, затраты на их приобретение окупаются, особенно когда речь идет о сложном производстве, например, кораблестроении, двигателестроении, машиностроении и аэрокосмической промышленности. Сейчас производители средств автоматического проектирования возлагают большие надежды на предприятия среднего и малого бизнеса, которых намного больше, чем промышленных гигантов. [7]
Средние. Ведущими компаниями этого типа являются системы SolidEdge (разработанная фирмой Intergraph, позже перекупленная и теперь принадлежащая UGS PLM Solutions (EDS)), SolidWorks одноименной компании (в настоящее время — подразделение Dassault Systemes), а также главным лидером и самым популярным продуктом является Inventor и Mechanical Desktop корпорации Autodesk. Это далеко не полный перечень средних САПР. Их популярность среди пользователей постоянно растет, и именно поэтому данная область очень динамично развивается. В результате по функциональным возможностям средний класс постепенно догоняет своих более дорогостоящих и тяжелых конкурентов. Однако совершенно не всем пользователям нужно такое разнообразие функций. Тем, кто работает с двумерными чертежами, прекрасно подойдет система легкого типа, которая стоит гораздо дешевле.
Легкие. Программы легкого сегмента служат для простого черчения в формате 2D, поэтому их обычно называют электронной чертежной доской. Хотя стоит сказать, что к настоящему времени этот тип и обрел некоторые трехмерные возможности.
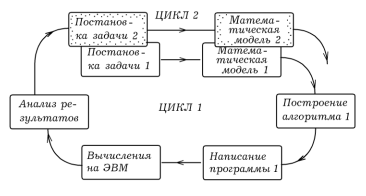
Рисунок 1 – Актуальность использования параметризации
Методы решения задач параметризации
Программирование в ограничениях и недоопределенные модели. Программирование в ограничениях (constraint programming) - достаточно новое направление в декларативном программировании. Появилось оно во многом в результате развития систем символьных вычислений, искусственного интеллекта и исследования операций.
Программирование в ограничениях является по своей сути максимально декларативным и основано на описании модели задачи, а не алгоритма ее решения. То есть программирвание в ограничениях - это своего рода програм-мирование в терминах "постановок задач". В общем случае постановка задачи - это конечный набор переменных x[1], ..., x[n], соответствующих им конечных (перечислимых) множеств значений X = {X[1], ...,X[n]}, и набор ограничений С = {C[1],...,C[m]}. Ограничения представлены как утверждения, в которые входят в качетсве "параметров" переменные из некоторого подмножества X[j],j=1..m набора X. [5] Решение такой задачи - набор значений переменных, удовлетворяющий всем ограничениям C[j].
Такая постановка задачи называется проблемой удовлетворения ограничений, а для ее решения используются различные алгоритмы и методы.
Теория «Концептуального програм-мирования». Этот алгоритм базируется на типе данных «неопределенное значение». Данный тип используется для описания переменных, которые пока что не определены не по типу, не по значению. Семантические модели задают переменные и отношения, имя модели задается в операторе задачи. В отношении задаются все возможные пути расчета всех переменных через прочие переменные, входящие в некоторое математическое выражение.
Различаются: входные переменные (значения задаются), выходные переменные (значения вычисляются), слабо связанные переменные (иногда задаются, иногда рассчитываются), сильно связанные (значения меняются отношением), определяющие переменные (значения определяют применимость отношения).
Имеются разрешимые и неразрешимые задачи, для которых путь построить невозможно. Затем генератор программ формирует программу как линейный вызов базовых функций, связанных по данным, в совокупности реализующих требуемый путь расчетов.
Относящийся к этому направлению аппарат недоопределенных моделей используется в широком спектре приложений и предоставляет принципиально новые возможности для решения задач в таких областях, как математические расчеты, инженерия знаний, проектирование, планирование.
Недоопределенная модель. В Н-моделях переменной сопоставляется недоопределенное значение (или Н-значение), являющееся оценкой реального значения-денотата на основе доступной нам в данный момент информаци. Н-значение является промежуточным между полной определенностью (точное значение) и полной неопределенностью (весь универсум) и может уточняться по мере получения более точных данных.
В процессе уточнения, т.е. при поступлении более точных данных, Н-значение становится все более определенным и в пределе может стать точным, т.е. равным денотату данной недоопределенной переменной (Н-переменной).
Это означает, что для Н-переменной, вне зависимости от ее типа, следует различать два значения - реальное неизвестное нам значение-денотат, которое она представляет, и ее текущее Н-значение, являющееся доступной оценкой этого реального значения.[4].
Недоопределенность может характеризовать не только значения параметров существующих объектов или процессов, но и виртуальных объектов, находящихся в процессе создания. В этом случае Н-значение выступает в качестве ограничения на вычисляемое значение.
Исследования
Все связи, именуемые параметрическими, можно условно разделить на категории:
- геометрические (параллельность, перпендикулярность, взаимоотношения и т.д.);
- топологические;
- математические (связь параметров разных элементов, блоков и уравнений);
- размеры.[2]
Предлагаемая вариационная параметризация базируется на построении макета или эскиза, а также накладывании ограничений, зависимостей параметров и связей на объекты. Алгоритм построения параметрической модели вариационного вида можно свести к нескольким шагам:
- Создание эскиза для нужного действия, впоследствии на который и накладывают параметрические связи;
- Далее уточняются параметры, размеры и значения. Определяются переменные и задаются зависимости;
- Производится выбранное действие, в котором значения параметров и операций уже имеет значение и влияние;
- В случае необходимости создания сборки взаимное положение компонентов сборки задаётся путём указания сопряжений между ними.
Вариационная параметризация позволяет легко изменять форму эскиза или величину параметров операций, что позволяет удобно модифицировать трёхмерную модель.[3]
Предлагаемая вычислительная модель M=(X=( X1, Xi, X0), R) состоит из ряда параметров:
- Х – множество параметров, значения которых могут принимать различный вид:
- X1 – определяет одно точное значение;
- Xi – интервальное значение параметра;
- X0 – обозначает не определенное значение;
- R – множество отношений между параметрами.[6].
Преимущества
Представленная идея вариационной параметрической модели позволит создавать проекты, которые будут иметь взаимосвязанные параметры. Возможность параметризировать трехмерную модель может значительно упростить создание объектов и оптимизировать работу над существующими проектами. Математическая модель будет изменять параметры автоматически подстраиваясь под внесенное редактирование уже готового объекта. Такой подход предлагается реализовать на языке LISP и интегрировать в среду САПР AUTOCAD.[11]
Выводы
В данной работе были рассмотренные последние достижения и разработки в области решения задачи параметризации, как Российских, так и зарубежных. Приведен обзор наиболее актуальных технологий.
Программирование в ограничениях стало за последнее десятилетие самым перспективным и быстро развивающимся направлением на стыке искусственного интеллекта и вычислительной математики.
Как видно, наиболее актуальной технологией в этой сфере является программирование в ограничениях, парадигма которого была предложена Российским ученым Нариньяни А.С. Эта технология широко применяется для решения разнообразного класса задач, включая задачи САПР и др. [12]
Литература
1. Параметрическое моделирование [Электронный ресурс]. - Режим доступа: https://ru.wikipedia.org/wiki/Параметрическое_моделирование.
2. Параметризация [Электронный ресурс]. - Режим доступа: http://www.sapr.ru/article.aspx?id=8064&iid=325.
3. Нариньяни А.С., Телерман В.В., Ушаков Д.М., Швецов И.Е. Программирование в ограничениях и
недоопределенныемодели //Информационные технологии №7, 1998. М., Издательство “Машиностроение”. - C.
13-22.
4. Григорьев А.В. Методы построения функций в специализированной оболочке для создания
интеллектуальных САПР // Искусственный интеллект. – Донецк, 2001 – №3 – C. 40–53.
5. Журнал «Сапр и графика». SprutCAD: особенности национальной параметризации [Электронный ресурс]. - Режим доступа: http://www.sapr.ru/article.aspx?id=7889&iid=319.
6. Программирования в ограничениях и недоопределенные модели, А.С.Нариньяни, В.В. Телерман,
Д.М. Ушаков, И.Е. Швецов // http://www.raai.org/about/persons/nariniani/N-MODEL2.doc.
7. Статья. Инструментарий компьютерного моделирования. // http://rvles.ieie.nsc.ru/parinov/taomodel/2.htm.
8. Клещев А. С., Артемьева И. Л.. Математические модели онтологий предметных областей. Часть 1.
Существующие подходы к определению понятия «онтология». // Научно – техническая информация, серия 2
«Информационные процессы и системы», 2001, № 2, с. 20 – 27.
9. Т. А. Гаврилова, В. Ф. Хорошевский. Базые знаний интеллектуальных систем. – С.-Пб.: Питер, 2001.
10. Кутателадзе С.С. Параметризация выпуклых изометрических задач. Сибирский журнал
индустриальной математики, 1998. Том 1, № 1.
11. Роговец Е.А., Григорьев А.В. Разработка программных средств, повышающих эффективность
решения задачи параметризации в САПР AUTOCAD // Информатика, управляющие системы, математическое
и компьютерное моделирование ИУСМКМ– 2016.
12. Роговец Е.А. Нечеткая математика и параметризация в САПР // Компьютерная и программная
инженерия - Донецк, 2015 - С. 184.