Автор перевода: Копица А.В.
Источник:Прогнозирование временных рядов: Прогнозирование цены акций—60.
Прогнозирование временных рядов: Прогнозирование цены акций.
Aaron Elliot,
Cheng Hua Hsu
Аннотация
Прогнозирование временных рядов широко используется во множестве областей.
В этой статье мы представляем четыре модели для прогнозирования цены акций с использованием входных
данных временных
рядов индекса S&P500. Среднее значение (мартингейл) и обычные линейные модели требуют самого сильного
предположения
о стационарности, которое мы используем в качестве базовых моделей.Обобщенная линейная модель (GLM)
требует меньших допущений,
но не может превзойти мартингейл. При эмпирическом тестировании модель RNN работает наилучшим образом по
сравнению с двумя другими
моделями, поскольку она будет обновлять входные данные через LSTMinstantaneously, но также не
превосходит мартингейл.
Кроме того, мы вводим алгоритм "онлайн–пакет" (OTB) и измерение расхождений,
чтобы проинформировать читателей о современном методе прогнозирования,
который не требует какой–либо стационарности или предположений о несмешивании данных временных рядов.
Наконец, чтобы применить эти прогнозы на практике, мы представляем основные торговые стратегии, которые
могут
создавать беспроигрышные ситуации и ситуации с нулевой суммой.
Вступление
Прогнозирование временных рядов – классическая проблема во многих областях, имеющая широкий спектр приложений с высокой отдачей. Центральной проблемой прогнозирования является предсказание значения(T+ 1) с учетом прошлых наблюдений(1), ..., Y (T)[3]. Для решения этой проблемы было применено множество типов моделей. В этой статье будет представлено сравнение четырех моделей, используемых для прогнозирования цен на акции во временных рядах
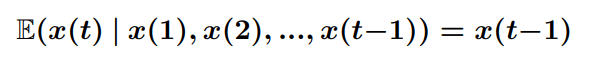(1)
где лучшее предположение для следующего значения, учитывая все состояния до настоящего времени, – это то, где мы сейчас находимся. Это может быть далее обобщено на
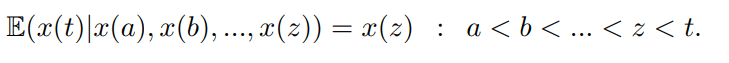(2)
лучшее предположение для любого значения в нашей последовательности, учитывая некоторую последовательность предшествующих состояний, – это самое последнее значение, которое мы знаем. Итак, если последовательность акций, которую мы наблюдаем, S, является мартингейлом, то наилучший возможный алгоритм для прогнозирования следующего значения – это просто текущее значение. Далее, в качестве контрапозитива, если мы можем показать модель, которая может последовательно превзойти модель Мартингейла, то мы показали, что существуют зависимости за пределами (2). Акции также моделируются как следующие геометрическому случайному блужданию [2]. Самое известное, что это моделирование было использовано при формулировке уравнения Блэка–Шоулза, уравнения, используемого во всем arXiv: 1710.05751v2 [stat.ML] 19 октября 2017
Наконец, часто считается, что акции имеют нестационарное поведение. Если событие изменяет способ взаимодействия ваших переменных (например, твиты Трампа, Brexit и т.д.), То это наблюдается как изменение в распределении , из которого отбираются наши случайные переменные. Все наши модели предполагают некоторую форму стационарности, хотя современные модели находят способ обойти это.
2.2 Линейная модель
Линейные модели формулируются таким образом, что переменная отклика (y) представляет собой линейную комбинацию переменной–предиктора или нескольких переменных–предикторов. Линейные модели предполагают: (1) отклик нормально распределен, (2) ошибки нормально распределены и независимы, и (3) что предсказатели фиксированы с постоянной дисперсией [5]. Предполагая, что запасы правильно смоделированы случайным блужданием с дрейфом, из этого следует, что
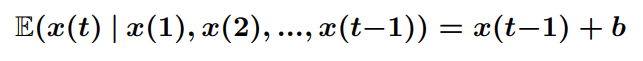(3)
Это поведение описывается линейной моделью: y(t) = βx(t − 1) + b.
2.3 Обобщенная линейная модель (GLM)
Обобщенные линейные модели расширяют линейные модели, позволяя ответу (1) быть нелинейно связанным с линейной комбинацией предикторов через функцию связи; (2) следовать любому распределению в экспоненциальном семействе (например, биномиальному, пуассоновскому, нормальному, гамма и т.д.); и (3) моделировать другие типы данных (например, категориальные, порядковые и т.д.) [5]. Оценка максимального правдоподобия весов предикторов обычно определяется с использованием метода Ньютона–Рафсона. GLMS предполагают (1) линейную зависимость между отклик, преобразованный функцией связи и линейной комбинацией предикторов, и (2) ошибки независимы. Однородность дисперсии предикторов не предполагается. Поскольку цена акций часто моделируется с использованием логарифмически нормального распределения, которое обладает желательными свойствами положительного и несимметричного, мы будем использовать GLM с нормальным распределением и функцией логарифмической связи для этого анализа. Предполагая, что акции правильно смоделированы с помощью геометрического случайного блуждания, из этого следует, что
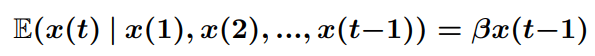(4)
Это поведение описывается GLM с функцией log link и «длиной памяти» в один образец. Для такого моделирования использовался пакет statsmodels python [6].
2.4 Рекуррентные нейронные сети
Рекуррентные нейронные сети (RNN) – это нейронные сети, которые имеют некоторый способ запоминания предыдущих значений, введенных в них, и вывода на основе как входных данных, так и запомненного значения. Это делается с помощью трех подпроцессов: элемента забывания, элемента ввода и элемента вывода. Предположим, что запомненное значение представляет собой вектор s внутри нейронной сети. Ворота забвения – это субнейронная сеть , которая, учитывая s, будет решать, какую часть s отбрасывать от итерации к итерации. Элемент обновления представляет собой субнейронную сеть, которая, учитывая входные данные x и текущее значение s, будет выводить новое значение для s.
Наконец, выходной элемент представляет собой субнейронную сеть, которая выдает выходные данные RNN в виде функции o (x, s). Что делает RNN особенно хорошими в прогнозировании данных временных рядов, так это то, что они позволяют выражать долгосрочные зависимости в выходных данных, но при этом не нуждаются в сложной архитектуре, позволяющей использовать входные данные переменного размера. Кроме того, если в наших временных рядах существуют долгосрочные зависимости, то нейронная Сеть, имеющая достаточное количество узлов, теоретически может их моделировать. На практике это менее реально. С нейронная сеть построена так, чтобы следовать градиентному спуску функции потерь, если более простая модель представляет собой локальные минимумы, то вполне вероятно, что модель застрянет в этих минимумах. Кроме того, если RNN сделать слишком сложным, он может обнаружить очень глубокие минимумы в своих обучающих данных, но только потому, что у него есть overfit. Наконец, RNN действительно предполагает стационарность; поскольку после завершения обучения устанавливаются веса сети.
Специально для этого анализа мы будем использовать рекуррентную нейронную сеть с длительной кратковременной памятью сеть (LSTM–RNN). LSTM–RNN делает еще один шаг вперед, используя эту архитектуру памяти в своих отдельных узлах. Для нашей архитектуры мы используем входной слой, соединенный со слоем узлов LSTM, за которым следует плотный слой из 1 узла для вывода. Эта архитектура была выбрана на основе первоначального тестирования с гиперпараметрами и на основе нашего набора данных размером 4000 записей.
2.5 Современный метод прогнозирования
Профессора Виталий Кузнецов и Мехриар Мохри из Института Куранта дают гарантии обучения алгоритмам
минимизации сожалений для прогнозирования нестационарных временных рядов без смешивания [5].
Ключевым техническим инструментом, который им нужен для нашего анализа, является мера расхождения, которая
количественно
определяет расхождение целевого и выборочного распределений, определяемое
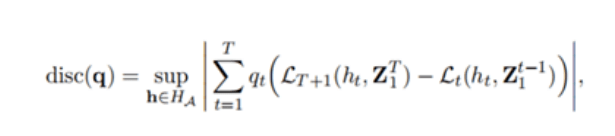(5)
где q = (q1, ..., qT) – произвольный весовой вектор, а где HA – набор последовательностей гипотез
который может выбрать онлайновый алгоритм A. Они смогли решить эту ограниченную задачу оптимизации
, сначала решив меньшую выпуклую задачу оптимизации для q∗. Тогда, если q∗ > 0, они могут гарантировать
, что решение задачи регрессии хребта ядра для несоответствия является выпуклым. Приводя к их выводу
о несоответствии. Сценарий онлайн–обучения не требует допущения о распределении. В режиме он–лайн
обучении последовательность раскрывается по одному наблюдению за раз, и часто предполагается, что она
генерируется
в состязательной манере. Цель ученика в этом сценарии – добиться сожаления, то есть
разницы между совокупной понесенной потерей и потерей лучшего эксперта в ретроспективе, которая растет
нелинейно со временем.
Используя алгоритм OTB, мы можем преобразовать наши исходные модели в динамические, которые будут обновлять информацию каждый раз, когда мы получаем новые данные, и мы можем продолжать корректировать экспертные веса в соответствии с самой последней ситуацией.
3 Данные
Данные о собственном капитале были получены из API данных временных рядов, поддерживаемого AlphaVantage [4]. Исторические данные об акционерном капитале доступны в 4 временных разрешениях: внутри дня, ежедневно, еженедельно и ежемесячно. Первоначально наши модели были протестированы на ежедневных ценах закрытия индексного фонда S&P 500 и его составляющих с 2000 года по настоящее время. Различные другие запасы использовались в каждом конкретном случае. Следует отметить, что цена акций не является постоянной с течением времени – рынки США открыты с С 9 утра до 4 вечера в рабочие дни, за исключением выходных и 10 праздничных дней.
4 Производительность модели
Эмпирическое тестирование линейной модели, обобщенной линейной модели и рекуррентной нейронной сети, по сравнению с базовым уровнем мартингейла, подробно описаны в следующих разделах.
4.1 Линейная модель
В ходе тестирования мы обнаружили, что линейная модель никогда не превосходила мартингейл и работала хуже, когда «память» модели (включая количество точек временной задержки) была увеличена. RMSE использовался в качестве показателя ошибок. Приведенные ниже тесты предсказывают цену акций SPX, используя предыдущий день или дни цен SPX. В первом выполненном тесте в качестве предиктора использовалось значение SPX за предыдущий день и были обучены весовые коэффициенты модели для данных за первые 12 лет (2000–2011 годы, примерно 70 процентов данных) и проверил прогнозы модели на данных за последние 5 лет (2012 – 2017, примерно 30 процентов данных). Несмотря на то, что это очень наивный тест, это разделение поезда / теста совпадает с разделением RNN для целей сравнения.
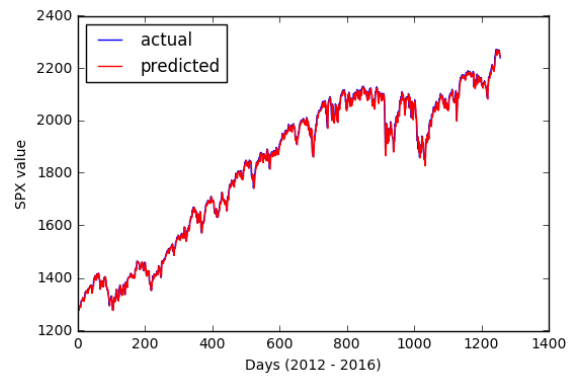
Рисунок 1. Производительность базовой линейной модели
В этом тесте модельный RMSE составил 15.168, в то время как соответствующий мартингейл RMSE составил 14.867. Во втором тесте использовалось то же разделение данных на поезд/ тест, но в качестве переменных ответа использовался набор значений SPX с разными временными задержками. Временные лаги были выбраны для включения значений за 1–4 дня до, за 1 неделю до, примерно за 1 месяц до и примерно за 1 квартал до, исходя из предположения , что моделирование периодических тенденций может повысить точность модели.
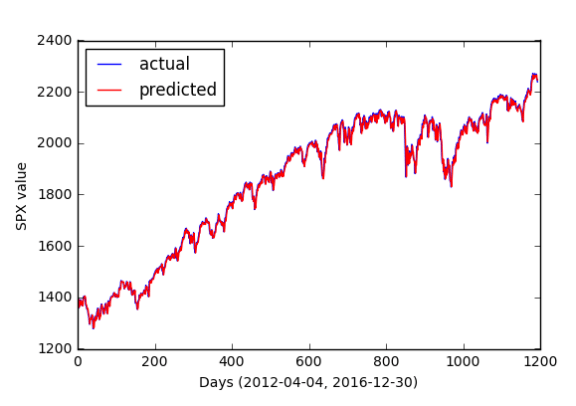
Рисунок 2. Производительность линейной модели с запаздыванием
GLAM, описанный в разделе 2.3, был впервые протестирован с использованием того же разделения данных о поездах/тестах 70/30 для модели, предсказывающей цену закрытия SXP по цене закрытия предыдущего дня.
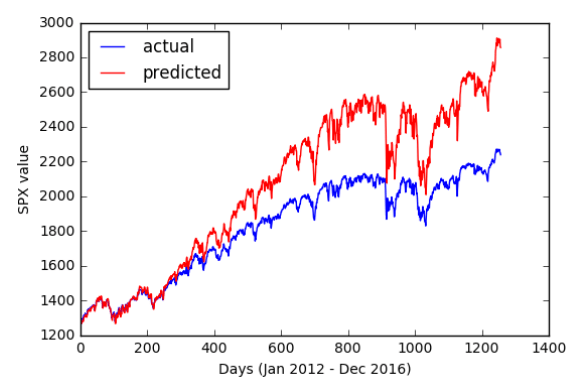
Рисунок 3. Прогнозирование цены закрытия SPX по цене SPX предыдущего дня; GLM обучен на данных из 2000–2011.
Предсказания модели сильно отличались от истинных данных (RMSE 290,5), особенно потому, что тестовые данные превышали диапазон значений, наблюдаемых в обучающих данных. Такое изменение не могло быть зафиксировано с помощью GLM с допущениями о стационарности. Чтобы решить эту проблему, был проведен второй тест путем разбивки данных обучения / тестирования на сегменты за один год, предполагая, что производительность GLM улучшится с более короткими периодами обучения / тестирования. Год с наименьшим RMSE показан ниже.
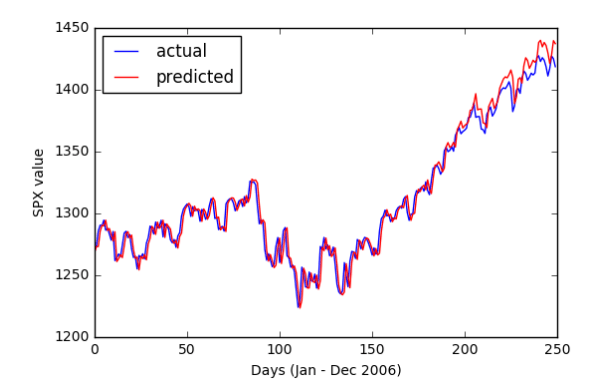
Рисунок 4. Прогнозирование цены закрытия SPX по цене SPX предыдущего дня; GLM обучен на данных из 2005–2006.
Опять же, мы обнаруживаем, что модель расходится к концу тестовых данных и что модель RMSE (8,91) больше, чем мартингейл RMSE (8,06). Мы обнаруживаем, что один год – это все еще слишком большой период , чтобы пройти до обновления веса – GLM просто не обобщает данные за длительные периоды времени. Онлайн–реализация GLM может иметь больше шансов превзойти режим мартингейла или соответствовать ему.
4.3 Рекуррентная нейронная сеть
При тестировании и уточнении нашего LSTM–RNN в сравнении с моделью мартингейла мы обнаружили, что в целом LSTM–RNN либо изучил мартингейл, либо сделал хуже, чем мартингейл. Было выполнено много итераций с различными комбинациями переменных. Для нетрансформированных ежедневных данных индекса S&P 500 200 узлов показали наилучшие результаты в нашем тестовом наборе со средней абсолютной ошибкой (MAE) 21,43307, в то время как мартингейл показал в два раза лучшие результаты с 10,53 509 MAE. Затем мы попытались преобразовать данные путем деления цены закрытия на цену открытия или процентное изменение. Это должно было соответствовать геометрической модели случайного блуждания.
Под этим преобразованием Было опробовано 10 узлов LSTM, результаты которых были умеренно хуже, чем у модели мартингейла. Мы также попытались преобразовать данные путем вычитания цены закрытия из цены открытия или абсолютного изменения.
Сопоставление модели случайного блуждания с гауссовым шумом. В рамках этого преобразования было опробовано 10 узлов LSTM, и они также показали умеренно худшие результаты, чем модель мартингейла.
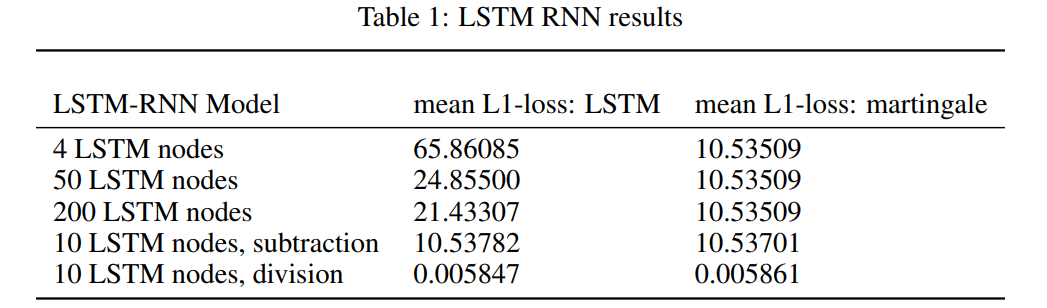
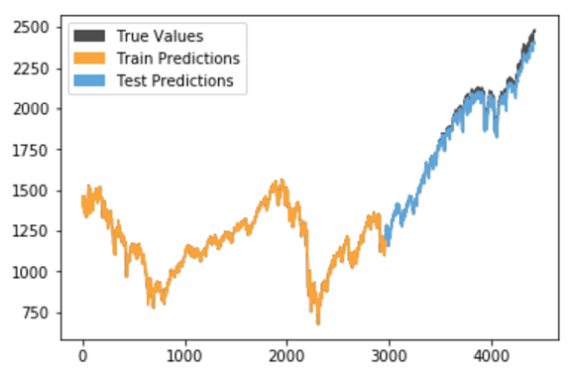
Рисунок 5. Производительность 200 узлов LSTM на данных SPX
В результатах по другим акциям, входящим в индекс S&P 500, мы получали лучшие результаты, когда данные тестирования находились в пределах диапазона обучающих данных, например, для Suntrust Banks Inc. (STI). На STI 4 узла показали хорошие результаты с 0,59893 MAE против 0,57283 MAE модели Мартингейла, результаты этого теста приведены на рисунке 6.
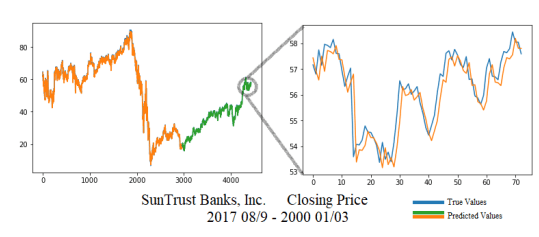
Рисунок 6. Производительность LSTM на основе данных Suntrust
Как видно на рисунке 6. LSTM отстает от истинного значения и в конечном итоге просто предсказывает , каким было предыдущее значение. Это было подтверждено, когда разница между двумя моделями была вычислена для этого теста и составила 0,09230 MAE. По сути, нейронная сеть научилась вычислять среднее значение. Это имеет смысл, поскольку среднее значение, как правило, является хорошим прогнозом и легко попадает в локальные минимумы для нашей модели. В заключение из наших результатов по LSTM–RNN. RNN не смог последовательно превзойти модель Мартингейла, и даже когда к данным были применены преобразования, чтобы заставить его прогнозировать закрытие что касается Мартингейла, то он всегда работал хуже. Это подтверждает идею о том, что эти акции правильно моделируются с помощью мартингейла.
5 Торговых стратегий для применения прогнозирования цен на акции
В следующих разделах представлены методы, обычно используемые в алгоритмической торговле и финансовой индустрии. Используя модели, о которых мы упоминали ранее, если мы сможем победить мартингейл, мы сможем получать прибыль от следующих торговых стратегий.
5.1 Использование опционов «колл» и «пут» для зарабатывания денег
Опцион – это контракт, который дает его владельцу право купить (опцион «колл») или продать (опцион «пут») финансовый актив (базовый) по фиксированной цене (цена исполнения) в фиксированную дату (дата истечения срока действия) или до нее. Если вы продаете короткую позицию (записываете) опцион, вы принимаете другую сторону сделки. Таким образом, вы можете войти в позицию 4 различными способами: купить колл, купить пут, продать короткую позицию колл, продать короткую позицию пут. И это со всеми возможными комбинациями цен исполнения и дат истечения срока действия. Премия – это цена, которую вы платите или собираете за покупку или продажу опциона. Это намного меньше , чем цена базовой акции. Основные рынки опционов обычно ликвидны, поэтому вы можете в любое время купить, записать или продать опцион с любой разумной ценой исполнения и датой истечения срока действия. Если текущая базовая цена (спотовая цена) опциона «колл» выше цены исполнения, опцион находится в деньгах; в противном случае он находится вне денег. Противоположное верно для опционов «пут». В деньгах хорошо для покупателя и плохо для продавца. Опционы в деньгах могут быть исполнены, а затем обменены на базовый актив по цене исполнения. Разница между спотом и страйком – это прибыль покупателя и убыток продавца. [8]
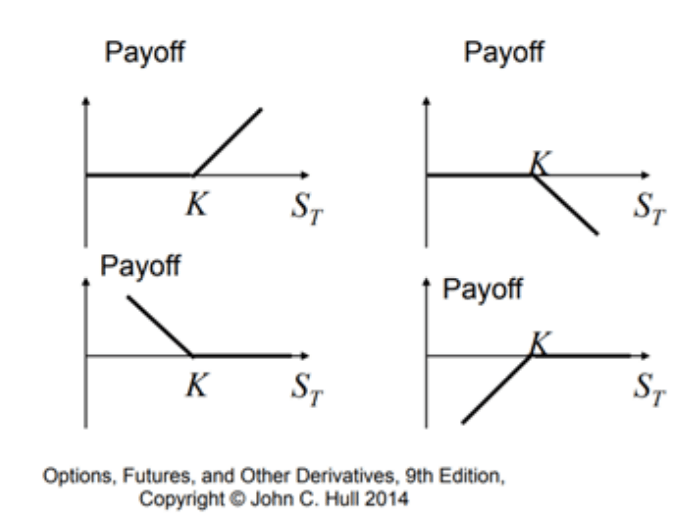
Рисунок 7. Опционы, фьючерсы, диревативы...
Где K = цена исполнения и St = цена акции . Поэтому, если мы сможем минимизировать функцию потерь в GLM и RNN, мы понесем меньшие потери при исполнении наших опционов «пут» и «колл». Поскольку прибыль от исполнения после вычета стоимости опционов «пут» и «колл» все равно будет больше или равна нулю.
5.2 Торговые стратегии
5.2.1 Арбитраж
Арбитраж – это разница рыночных цен между двумя разными субъектами. Арбитраж широко практикуется в глобальном бизнесе. Например, компании могут воспользоваться более дешевыми поставками или рабочей силой из других стран. Эти компании способны сократить расходы и увеличить прибыль. Арбитраж также может быть использован при торговле фьючерсами на S&P и акциями S&P 500. Это типично для фьючерсов на S&P и Акции S&P 500 для развития ценовых различий. Когда это происходит, акции, торгуемые на NASDAQ а рынки NYSE либо отстают, либо опережают фьючерсы S &P, предоставляя возможность для арбитража. Высокоскоростная алгоритмическая торговля может отслеживать эти движения и получать прибыль от разницы в ценах.
5.2.2 Возврат к среднему значению
Возврат к среднему значению – это математический метод, который вычисляет среднее значение временных максимумов и минимумов цен ценной бумаги. Алгоритмическая торговля вычисляет это среднее значение и потенциальную прибыль от движения цены ценной бумаги, когда она либо отклоняется от средней цены, либо приближается к ней.
5.2.3 Скальпинг
Скальперы получают прибыль от торговли спредом bid–ask как можно быстрее много раз в день. Движение цены должно быть меньше, чем спред ценной бумаги. Эти движения происходят в течение нескольких минут или меньше, что приводит к необходимости принятия быстрых решений, которые могут быть оптимизированы с помощью алгоритмических торговых формул.Другие стратегии, оптимизированные с помощью алгоритмической торговли, включают снижение транзакционных издержек и другие стратегии , относящиеся к темным пулам.[7] При разработке алгоритма «онлайн–пакет» эта стратегия может быть легко реализована.
5.3 Беспроигрышная игра или игра с нулевой суммой
Независимо от того, какую торговую стратегию мы используем, хороший алгоритм всегда может минимизировать наши потери без дополнительных затрат на транзакцию, поэтому беспроигрышная игра возможна даже тогда, когда мы сталкиваемся со структурными изменениями или внезапным сбоем в рыночном механизме. С другой стороны, при тщательном выборе портфеля опционов «пут» и «колл» мы можем предотвратить потерю слишком больших денег из–за ошибок прогнозирования, которые в конечном итоге, по крайней мере, создадут ситуацию с нулевой суммой в долгосрочной перспективе. Наиболее важным является то, что: этот торговый алгоритм и стратегию нетрудно реализовать и использовать непрофессионалам или обычным пользователям пользователи.
Заключение
Целью данного исследования являлась разработка прогностической модели для прогнозирования данных финансовых временных рядов. В этом исследовании мы рассмотрели 5 и разработали 4 прогностические модели. Среднее значение и анализ линейной регрессии подразумевают, что прогнозные значения и реальные значения отклоняются от среднего. Затем мы берем модель GLM и RNN по сравнению со средней и обычной линейной моделью. Эмпирические исследования точности прогнозирования временных рядов цен (путем сравнения показателей прогнозирования, таких как MAY и RMSE) показывают, что предлагаемые модели (GLM, LSTM–RNN) не улучшают точность прогнозирование 1–мерных временных рядов. Дальнейшее совершенствование с использованием современных методов может быть использовано с торговыми стратегиями, упомянутыми в разделе 5, для извлечения выгоды из прогнозов цен на акции.
Использованная литература
- 1. Шрив, Стивен Э. Стохастическое исчисление для финансов I Биномиальная модель ценообразования активов. Спрингер, 2005.Александер, Дж.А.
- 2. Пински, Марк А. и Сэмюэл Карлин. Введение в стохастическое моделирование. Академическая пресса, 2011.
- 3. Виталий Кузнецов и Мехрияр Мохри. Прогнозирование временных рядов и онлайн–обучение. В материалах 29–й ежегодной конференции по теории обучения (COLT 2016). Нью–Йорк, США, июнь 2016 года.
- 4. https://www.alphavantage.co/documentation
- 5. Введение в обобщенные линейные модели. Пенсильванский государственный университет, Научный колледж Эберли. https://onlinecourses.science.psu.edu/stat504/node/216
- 6.https://www.statsmodels.org
- 7. Халл, Дж. (2006). Опционы, фьючерсы и другие производные финансовые инструменты. Аппер–Седл–Ривер, Нью–Джерси: Пирсон/Прентис Холл.
- 8. https://www.investopedia.com/terms/a/algorithmictrading.asp
- 9. Алгоритмическая торговля опционами, часть 1 http://www.financial-hacker.com/algorithmic-options-trading/8