ИССЛЕДОВАНИЕ ТЕРМОДИНАМИКИ ТЕНЗОМЕТРИЧЕСКИХ ВЕСОВ И РАЗРАБОТКА МЕТОДОВ СНИЖЕНИЯ ИХ ТЕМПЕРАТУРНОЙ ПОГРЕШНОСТИ

Описание

Мы провели исследование термодинамики многокомпонентных тензометрических весов и предложили меры по снижению их температурных погрешностей из-за нестационарных пространственных градиентов температуры. Разработана и экспериментально апробирована балансовая термодинамическая модель, основанная на методе электротермической аналогии. Предложен способ корректировки вариаций нулевого значения тензометрических весов в ходе эксперимента. Измерение воздействия газового потока на модель летательного аппарата является одной из основных задач экспериментальной аэродинамики. Измеряются кумулятивные и распределенные аэродинамические нагрузки, действующие на модель. Общая нагрузка измеряется с помощью многокомпонентного аэродинамического баланса. В большинстве случаев шестикомпонентные тензометрические весы легко адаптируются к условиям эксперимента и используются для широкого класса тестовых моделей. Требования к балансировочным грузам для измерения деформации диктуются характеристиками газа, такими как рабочий поток в аэродинамических трубах, конфигурация и размер моделей, срок службы рабочего процесса и другие факторы. Одной из главных проблем при разработке весов является получение заданной точности измерений. Если технология балансировки, начиная с проектирования и заканчивая калибровкой, поддерживается должным образом, проблема заключается в температурной погрешности во время ее эксплуатации. Существует две составляющие температурной погрешности: статическая и динамическая. Статическая составляющая температурной погрешности проявляется в установившемся тепловом режиме весов, когда температура всех его элементов изменяется одновременно без градиентов. Эффективное уменьшение статической составляющей обеспечивается схематически, например, путем включения термокомпенсаторов из меди или никеля в соответствующее плечо моста последовательно с деформацией. Результаты компенсации достигаются за счет конкретного значения остаточной статической температурной погрешности в диапазоне измерений менее (1-2) х 10-3 %/T C. Расчеты и испытания показывают, что весы практически никогда не работают при стационарных тепловых режимах. Причина заключается в тепловой инерции весов, в то время как температура потока и режимы испытаний меняются с течением времени. В результате весы имеют пространственно-временные температурные градиенты, и температурная компенсация, обеспечиваемая при стационарных тепловых режимах, не только теряет свою эффективность, но и может привести к увеличению погрешности.

1. ИССЛЕДОВАНИЕ ТЕРМОДИНАМИКИ ТЕНЗОМЕТРИЧЕСКИХ ВЕСОВ

В данном исследовании задача уменьшения динамической составляющей температурной погрешности была выполнена с помощью сочетания теоретических и экспериментальных методов исследования с учетом термодинамики весов. Для расчета температурных градиентов мы разработали балансовую дискретную тепловую модель, основанную на методе электротермической аналогии. Динамика теплового режима моделируется в виде электрической цепи (показано на рис. 1). Таким образом, каждый компонент схемы имитирует отдельный дискретный элемент баланса. К каждому элементу подается напряжение, соответствующее температуре окружающей среды (Uc) и температуре модели (Um).

Сопротивление Rk (k = 1,..., n, где n - количество дискретных элементов) имитирует конвективный теплообмен k-го дискретного элемента через боковую поверхность с внешней средой и определяется где a - коэффициент теплопередачи, а Sk - площадь боковой поверхности дискретного элемента. элемент. Сопротивление rk имитирует теплопередачу между отдельными элементами внутри весов через площадь поперечного сечения sk и выражается через:

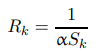
где 2 lk - длина k-го дискретного элемента, а A - коэффициент теплопроводности материала. Емкость Ck численно равна теплоемкости k-го дискретного элемента. Он представлен:

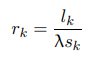
где pk - весовой коэффициент, а co - удельная теплоемкость.

Значения электрического потенциала cpc, как показано на схеме, соответствуют температуре в конкретной точке, а значения электрических токов - тепловому потоку. Значение коэффициента теплопередачи а уточняется экспериментально для расчета,

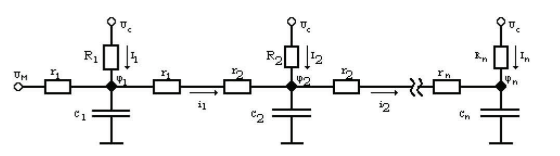
Рисунок 1 – Электрическая схема.

чтобы наилучшим образом соответствовать экспериментальным данным. В конце концов, для решения системы из n дифференциальных уравнений первого порядка следующего вида:

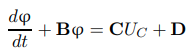
где B, C и D - матрицы, состоящие из параметров схемы, определенных из уравнений Кирхгофа.

На основе анализа эластичной схемы баланса мы вывели формулы и параметры, определяющие чувствительность отдельных компонентов к температурному градиенту. В результате теоретических и экспериментальных исследований были разработаны технологические мероприятия по снижению чувствительности к температурным градиентам. Хороший эффект достигается за счет нанесения покрытий из теплоизоляционных и уравнивающих тепло материалов. Первое может снизить скорость нагрева конкретного элемента и сделать его тепловое состояние более предсказуемым, а второе может уменьшить температурный градиент.

На рисунке 2 показаны шестикомпонентные тензометрические весы внутренней модели диаметром 40 мм с диапазоном измерения нормальной силы 4200 Ньютон. На рисунке 3 показаны расчетные и экспериментальные диаграммы реакции теплоизолированного компонента X баланса на скачок температуры окружающей среды в термостате. График показывает, что рассчитанная модель удовлетворительно предсказывает тепловую динамику X-компонента баланса.

а рисунке 4 показана функция температуры трех точек балансовой структуры (Ti, T2 и T3) без теплоизоляции от времени при нагревании в термостате. На графике видно, что наибольшее расхождение кривых происходит в диапазоне температур 40-80°C. Указанный диапазон характеризуется максимальной скоростью нагрева баланса. При дальнейшем нагревании скорость уменьшается, и кривые сходятся. Абсолютное расхождение температур достигается при ~ 4°C, что существенно для компонента X.

Рисунок 2 – Вид в сборе тензометрических весов внутренней модели с изолирующим покрытием.

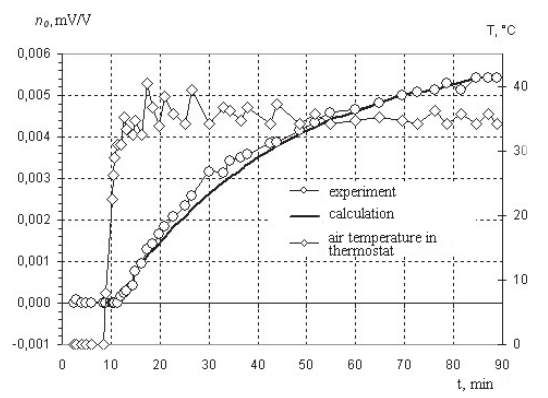
Рисунок 3 – Диаграмма реакции теплоизолированного компонента X на скачок

температуры окружающей среды в термостате.

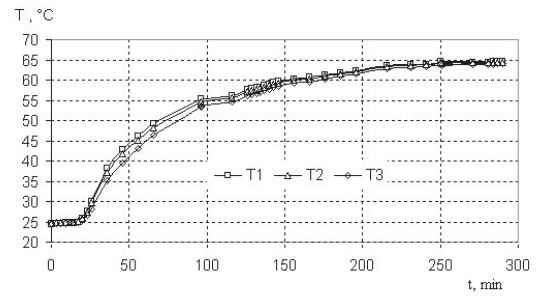
Рисунок 4 – Функция температуры трех точек баланса конструкции без

теплоизоляции от времени при нагревании в термостате.

На рисунке 5 представлена функция температуры в те же моменты времени для баланса после нанесения теплоизоляции при нагреве. На графике не видно расхождения кривых, что доказывает сбалансированный нагрев без градиента. Три области кривых, хорошо видимые на графиках, соответствуют трем скачкам температуры термостата

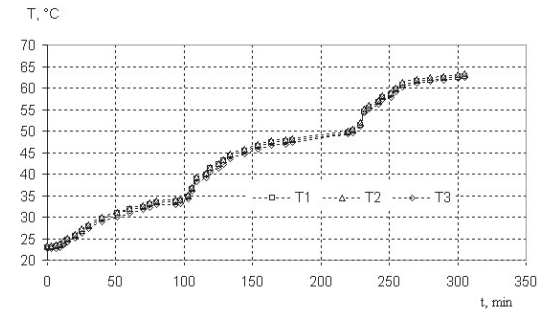
Рисунок 5 – Функция температуры трех точек структуры баланса времени после

нанесения теплоизоляции при нагреве.

и, соответственно, три области графика с максимальной скоростью нагрева. Как бы то ни было, расхождения между кривыми практически отсутствуют.

Сравнение графиков на фиг. 4 и 5 показано, что теплоизоляция уменьшает температурные градиенты. Графики на рис. 4 приведены дисперсионные кривые T\, T2 и T3 на сбалансированных участках нагрева с термостатом примерно в 2-3 раза выше, чем на рис. 5.

На рисунке 6 показана функция относительных ошибок дрейфа нуля для всех компонентов баланса средней температуры структуры (Ti + T2 + Тз)/3, при этом ошибки относятся

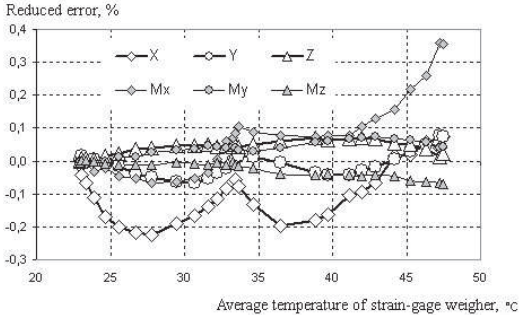
Рисунок 6 – Функция относительного дрейфа ошибок нулей для всех компонентов баланса (в

пределах диапазона измерений) средней температуры конструкции.

к диапазону измерения компонентов. Данные рис. 6 показывают, что ошибки дрейфа баланса термодинамики для рис. 5 диапазон условий нагрева от 23 до 47°C не превышайте следующих значений для каждого компонента:

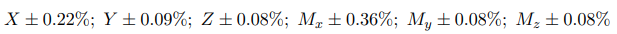
Приведенные выше данные показывают, что разработанные меры обеспечивают значительное снижение чувствительности баланса к термодинамике нагрева.

2. СПОСОБ КОРРЕКТИРОВКИ ВАРИАЦИЙ НУЛЕВОГО ЗНАЧЕНИЯ ТЕНЗОМЕТРИЧЕСКИХ ВЕСОВ В ХОДЕ ЭКСПЕРИМЕНТА

Давайте рассмотрим влияние изменений температуры на показания тензометрических весов, которые удовлетворяют конструктивным требованиям, изложенным в разделе 1, при испытаниях в аэродинамической трубе Т-128. Типичное изменение показаний трех датчиков температуры весов и предварительной камеры в зависимости от времени запуска показано на рис. 7 для так называемого разогретого состояния весов; модель и весы были разогреты во время предыдущих испытаний. Время начала соответствует измерению нулевых показаний перед экспериментом. Три испытания (полярные) были проведены при числах Маха M = 0,9, 0,6 и 0,3, соответственно, на этапе запуска. После запуска весы и модель обычно охлаждаются, поскольку их температура выше, чем температура воздуха в рабочей зоне. Во время первого испытания весы продолжают охлаждаться, в то время как температура потока увеличивается. Когда температура в предварительной камере повышается до 7,5°C, температура передней части весов

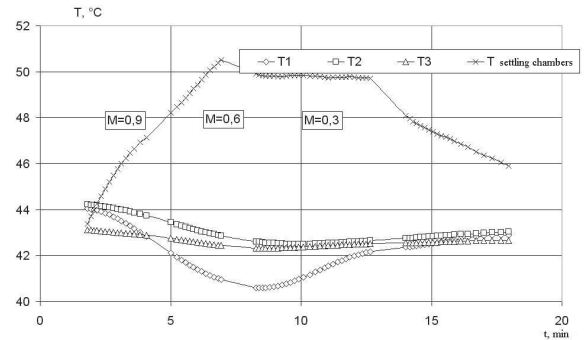
Рисунок 7 – Температурные колебания температуры баланса и трубки предварительной камеры во

время пуска.

(точка Ti), опускается до AT = -3,5°C. Начиная со второго поляра, температура баланса возрастает более резко во фронтальной части. Это доказывает, что основной тепловой поток распространяется от нагретой носовой части модели через весы к хвостовой части. Следует отметить, что наряду со сбалансированным изменением средней температуры изменяется и ее градиент. В целом, мы можем сказать, что динамика изменения температуры носит очень сложный характер.

Давайте рассмотрим показания My, компонента, которые были получены в ходе серии испытаний, состоящей из 86 пусков труб, для внутренних тензометрических весов, показанных на фиг. 2. Стандартное отклонение (SD) после калибровки весов составляет 0,1%. Значения нулевых показаний тензометрического балансировочного моста, выраженные в процентах от его диапазона, в зависимости от количества пусков, представлены на фиг. 8. Отдельный значок показывает нулевые показания до и после эксперимента. Значения SD для нулевых показаний до и после эксперимента показаны на диаграмме. Эти нулевые показания были получены путем пересчета измерений во время эксперимента по методу, представленному ранее [1], и они согласуются с нулевыми показаниями, полученными при калибровке весов на стенде: отсутствие нагрузки на тензометрические весы, нулевые значения крена баланса и углов тангажа. Стандартное отклонение нулевых показаний компонента My до и после опыта для всей серии тестов (выраженное в процентах от диапазона) составило 0,08%. Это значение всего на 0,02% меньше значения, полученного при калибровке весов, соответствующего значениям, полученным в тепловой камере и представленным в разделе 1.

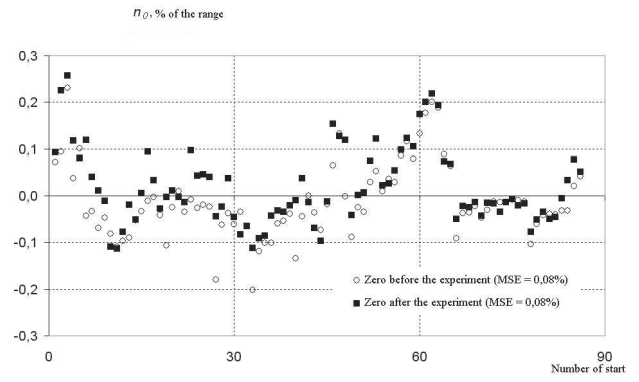
Рисунок 8 – Значения нулевых показаний компонента My в зависимости от количества запусков. Значение равно нулю до и после теста.

Изменение нулевых показаний во время эксперимента, в зависимости от количества запусков, показано на рис. 9, где функция представляет случайный характер. Значение SD вдвое меньше, чем 0,042%.

Выразим изменение функции нулевых показаний в виде линейной комбинации показаний датчиков температуры баланса и времени запуска следующим образом:

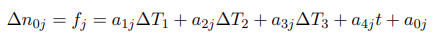
где j - номер компонента баланса (j = 1,2,... 6); A n0j - изменение показаний нуля во время запуска для j-го компонента (в милливольтах на вольт); AT1, AT2, AT3 - изменение показаний датчиков температуры во время запуска (в градусов Цельсия); и t - время между измерениями нулевых показаний до и после опыта (в минутах). Фактически, эта функция является аппроксимацией решения уравнения теплопроводности на существующем количестве экспериментальных точек.

Коэффициенты, определенные методом наименьших квадратов, представлены в таблице 1. Давайте оценим вклад каждого элемента для следующих конкретных значений экспериментальных данных: при ~ 30 мин, ПРИ1 ~ ПРИ2 ~ ПРИ3 ~ 10°C. Результаты оценок представлены в таблице 2.

Можно отметить, что для компонента My весов температура первого датчика вносит наибольший вклад в изменение нулевого значения, в то время как время запуска вносит незначительный вклад. Зависимость изменения нулевого значения от аппроксимирующей функции f5 показана на рис. 10. Значения коэффициента корреляции R2 и SD составляют 0,96 и 0,008% соответственно.

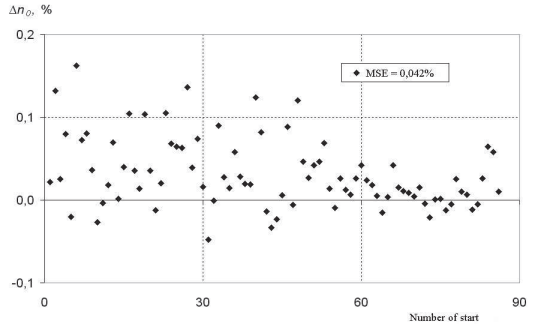
Рисунок 9 – Изменение компонента нулевого считывания My во время эксперимента в зависимости от количества запусков.

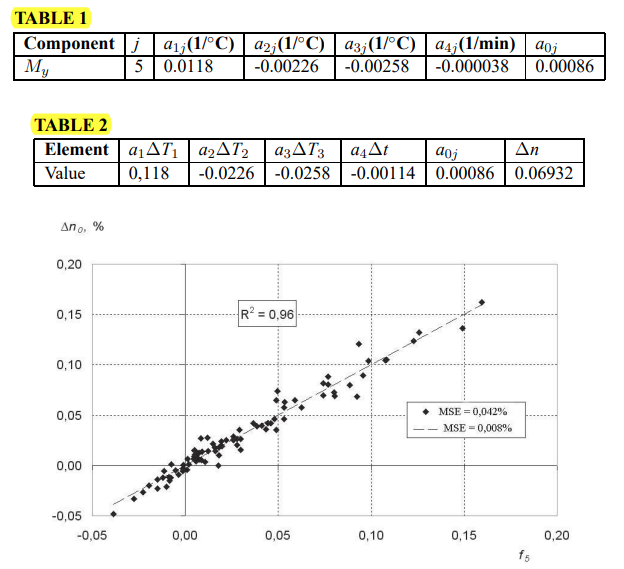
Рисунок 10 – Зависимость изменения нулевой составляющей показаний My весов для измерения деформации во время эксперимента от аппроксимирующей функции f5.

Коэффициент корреляции достаточно высок, что подтверждает возможность применения линейной зависимости изменения нулевых показаний и температуры баланса. Остаточная погрешность баланса (SD = 0,008%) в 12 раз меньше, чем погрешность, полученная при калибровке, в 10 раз меньше, чем значения, представленные на рис. 6, и в пять раз меньше, чем SD отклонения нулевых показаний в течение всей серии испытаний. Для других компонентов мы получили следующие значения погрешности: X = 0,061%; Y = 0,023%; Z = 0,014%; Mx = 0,043%; и Mz = 0,022%. Значения погрешностей оказались в 3,6-8,4 раза меньше значений, показанных на рис. 6.

Таким образом, предлагаемый способ обеспечивает значительное снижение случайных ошибок измерения нагрузки с помощью тензометрических весов. Это очень важно при тестировании моделей с небольшой геометрической конфигурацией, которые обеспечивают небольшие колебания нагрузки на весы. Кроме того, этот метод позволяет проводить несколько испытаний за один прогон в аэродинамической трубе, тем самым повышая производительность и снижая затраты на одно испытание.

По сравнению с обычным методом (использующим нулевые показания до или после эксперимента или в качестве среднего арифметического), этот метод уменьшает погрешность в пять раз для компонента My весов. Очевидно, что такое значительное снижение погрешности может быть достигнуто только при использовании высококачественных разработанных и изготовленных весов.

На основе приведенного выше анализа данных для трансзвуковой аэродинамической трубы Т-128 был предложен следующий метод учета изменения нулевых показаний весов. Для каждого экспериментального испытания и компонентов весов значение приращения нулевых показаний, соответствующее калибровке весов, вычисляется в соответствии с уравнением (1), при этом значение коэффициента корреляции для аппроксимирующей функции fj равно 1. Для меньших значений коэффициента корреляции, которые обычно встречаются в эксперименте, текущее значение нулевых показаний определяется как линейная зависимость от функции fj, которая должна быть найдена с помощью

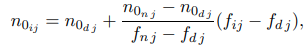
где j - номер компонента баланса (j = 1, 2,... 6); индекс d соответствует значениям до эксперимента, индекс n соответствует значениям после эксперимента; v - текущее значение компонента нулевых показаний j для i-го кадра; fij - текущее значение аппроксимирующей функции для i-го кадра и j-го компонента баланса. В этом случае, в отличие от уравнения (1), рассчитанные и измеренные нулевые показания до и после эксперимента совпадают. Уравнения (1) и (2) дают одинаковые результаты, когда коэффициент корреляции в точности равен 1.

Если значения fj или нулевых показаний не изменяются после эксперимента, то текущее значение нулевых показаний вычисляется по следующей формуле (неопределенность раскрывается в уравнении. (2) от L'Hopital):

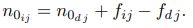
Для весов без датчиков температуры время может быть использовано в качестве аргумента f.

Выводы

Была разработана и экспериментально протестирована балансовая тепловая модель. Показано, что хороший эффект в снижении чувствительности внутримодельного баланса к температурным градиентам был достигнут за счет применения теплоизоляционных покрытий и тепловыделяющих материалов.

Предложен способ регулировки отклонения нулевого показания, позволяющий в несколько раз снизить систематические погрешности из-за влияния температурного градиента до 0,01-0,05%. Это, в свою очередь, позволяет проводить несколько испытаний за один прогон в аэродинамической трубе для повышения производительности и снижения стоимости испытания. Метод использовался при обработке результатов испытаний тензометрических весов внутренней и внешней моделей в аэродинамической трубе Т-128 более десяти лет.

Список использованной литературы

1. Горбушин А. Р. Способ определения веса модели и динамометра по показаниям тензометрических весов // Научные труды Центрального университета. Инст., том. XL, № 4, стр. v-v, 2009.