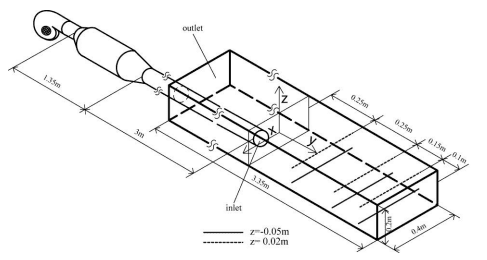
Рисунок 1. Принципиальная схема испытательной секции
Авторы: M Branny, M Jaszczur,W Wodziak, J Szmyd
Автор перевода: Наумов М. А.
Источник: 7th European Thermal-Sciences Conference (Eurotherm 2016)
Аннотация. В данном исследовании обобщены результаты экспериментальных испытаний и численного моделирования воздушного потока в лабораторной модели тупиковой выработки, проветриваемого системой принудительной вентиляции. Целью исследования является качественная и количественная верификация данных компьютерного моделирования. Компоненты вектора скорости измеряются с помощью велосиметрии изображения частиц. В численных расчетах использовались две модели турбулентности, стандартная модель k‐ε и модель нагрузки Рейнольдса. Сравнение величины вектора скорости и кинетической энергия турбулентности, полученная экспериментальными методами и численными расчетами, показывает, что в качественном выражении прогнозируемое поле скоростей хорошо коррелирует с данными измерений. Средняя относительная погрешность между результатами расчетов и измерений для величины вектора скорости и кинетической энергии турбулентности составляет около 29% для модели нагрузки Рейнольдса и 33% для стандартной модели k‐ε.
1. Введение Горные выработки с рабочими забоями тупиковых выработок обычно вентилируются с помощью систем вентиляторов и воздуховодов. В польских угольных шахтах система нагнетания, вентилятора и воздуховодов часто используется для вентиляции тупиковых штреков и выработок. Расстояние от входа струи до тупиковой стенки выработки не превышает 10м, в метановых шахтах - 8м. Поле скоростей, создаваемое потоком подаваемого воздуха, полностью трехмерно, а поток является турбулентным. В настоящее время параметры воздушных потоков определяются с использованием подхода CFD (Вычислительная гидродинамика). В инженерных приложениях чаще всего используются модели RANS (среднее значение Рейнольдса Навье‐Стокса).
В данной статье представлены результаты экспериментального тестирования и численного прогнозирования воздушного потока в лабораторной модели тупиковой выработки, проветриваемого системой принудительной вентиляции. Геометрический масштаб физической модели составляет 1:10. Стенки модели гладкие, поперечное сечение выработки прямоугольное, а наличие горных машин и оборудования в канале не учитывается. Измерения проводились для стационарных и изотермических условий течения. В этом случае равное число Рейнольдса в модели и реальном объекте гарантирует, что критерии потока схожи. Компоненты вектора скорости были измерены с использованием метода велосиметрии изображения частиц (PIV). Численные процедуры, представленные в этой статье, используют две модели турбулентности: стандартную модель k‐ε и модель напряжений Рейнольдса (RSM). Численные расчеты с граничными условиями, аналогичными тем, которые использовались в экспериментальных исследованиях, поддерживаются программой Ansys Fluent. Основной целью данного исследования является качественная и количественная проверка результатов компьютерного моделирования.
Исследования по валидации моделей турбулентности, используемых в шахтной вентиляции, были проведены в [1], [2]. Авторы сравнили результаты измерений поля скоростей [1] и концентрации метана [2] с численным прогнозом для воздушного потока в забойных выработках. Они подсчитали, что результаты, полученные с помощью моделей Spalart‐Allmaras и SST k‐ω, согласуются с экспериментальными данными. Экспериментальная проверка моделей турбулентности воздушного потока на пересечении забоя с вентиляционным проходом была представлена в [3]. Воздушный поток, исследованный в этой статье, отличается от тех, которые анализировались в [1], [2], [3] где соединения между вентиляционными каналами были расположены по‐другому. Валидация моделей турбулентности, используемых при компьютерном моделировании воздушных потоков в глухих выработках, была проведена в работах [4], [5], [6] и [7]. Авторы [8] сравнили результаты численного моделирования с результатами измерений продольных составляющих скорости, полученными в реальном объекте. В численных расчетах они использовали модель Спаларта‐Аллмараса. Ошибка в прогнозируемых значениях продольных составляющих скорости оценивалась примерно в двадцать процентов.
Авторы [5], [6] и [7] использовали результаты измерений, полученных Parra [4], для проверки четырех моделей турбулентности, а именно моделей Спаларта‐Аллмараса, k‐ε, k‐ω и RSM. Учитывая время вычислений и относительно небольшую относительную погрешность до 15%, авторы [5] обнаружили, что поле скоростей, полученное с использованием модели Спаларта‐Аллмараса, было определено с достаточной точностью для практических целей. С другой стороны, по данным авторов [6] и [7], ошибка в прогнозируемых значениях продольных составляющих скорости составила 36‐72% для модели Спаларта‐Аллмараса, 15‐51% для k‐ε, 37‐93% для k‐ω и 5‐70% для RSM. Результаты валидации двух моделей турбулентности (k‐ε и RSM) в случае воздушного потока через длинную глухую камеру были представлены в [8]. Предметом данной статьи является продолжение исследования, описанного в [9]. В отличие от работ, представленных выше, экспериментальная проверка выбранных моделей турбулентности в этой статье была выполнена на основе измерений трех (средней и флуктуирующей) составляющих вектора скорости и для трех различных чисел Рейнольдса.
2. Экспериментальная установка
Экспериментальные измерения проводились в лабораторной установке, состоящей из прямоугольного канала длиной 3,35м и площадью поперечного сечения 0,4м x 0,2м. На рисунке 1 показана настройка для измерения. Система подачи воздуха на лабораторный стенд была такой же, как в [9]. Расстояние между осью трубы подачи воздуха от верхней и боковых стенок канала составляло 0,08м и 0,75м от входа струи до тупиковой стенки. Эксперимент был проведен для получения поля скоростей в измерительной секции испытательной установки с использованием методики PIV. В реальном потоке число Рейнольдса (основанное на гидравлическом диаметре подводящего трубопровода в качестве характерного размера и средней скорости) обычно превышает 100 000. Измерения были выполнены для скоростей воздушного потока во впускном канале 15,4 м/с, 21,2 м/с и 35,4 м/с, что дало числа Рейнольдса около 78000, 108000 и 180000 соответственно.

Рисунок 1. Принципиальная схема испытательной секции
3. Сравнение экспериментальных и численных результатов
На рисунке 2 показаны контуры поля скоростей, полученные в результате измерений и численного моделирования в горизонтальном поперечном сечении, расположенном на уровне воздуховода и на 5см выше дна выработки. Предсказанное поле скоростей с использованием обеих моделей турбулентности качественно хорошо согласуется с экспериментальными данными.
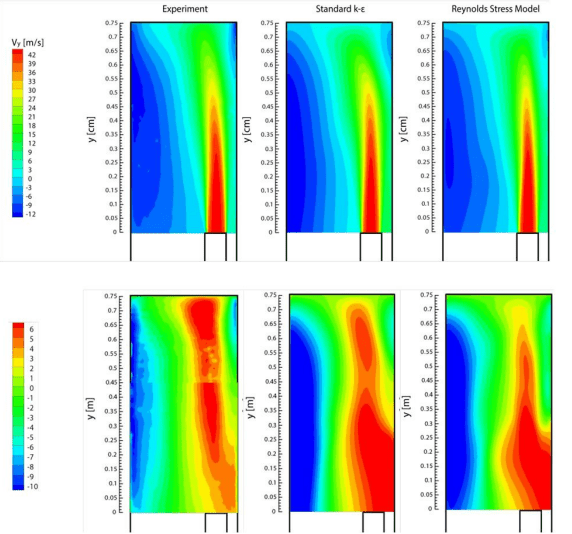
Рисунок 2. Контуры продольной составляющей скорости в горизонтальной плоскости на уровне выше - по оси подводящего канала, ниже – в 0,05м от дна выработки
Экспериментальные и численные данные количественно сравниваются на рисунке 3. На этом рисунке показаны распределения величины вектора скорости вдоль выбранных линий поперечного сечения выработки. Горизонтальные линии определяются координатами x [-0,2м, 0,2м], z=0,02м (ось подводящего канала) и z=-0,05 м (5см от дна выработки) и расположены на расстояниях y=0,25м и 0,65м от входного отверстия. Средняя относительная погрешность между измеренной и рассчитанной величинами скорости составила 29% для модели RSM и 33% для модели k‐ε. Наиболее значительные расхождения между данными измерений и расчетов получены в нижней части выработки (z=-0,05м). В этой локальной зоне максимальная относительная погрешность составляет около 100%.
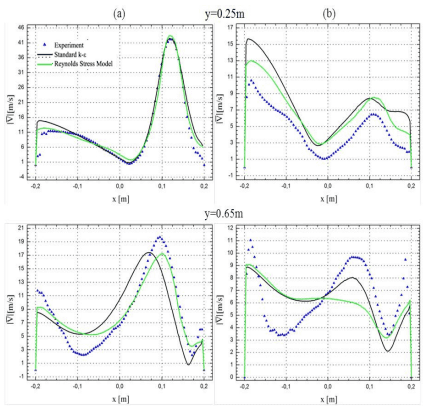
Рисунок 3. Сравнение величины вектора скорости |
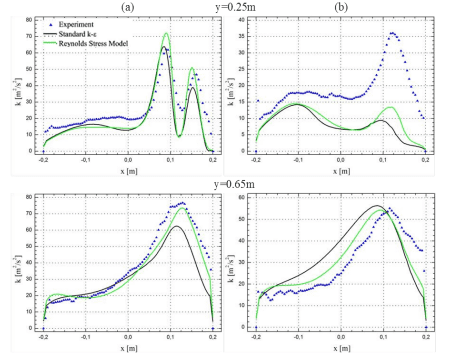
Рисунок 4. Сравнение кинетической энергии турбулентности k вдоль выбранных линий на уровне (a) оси подводящего канала; (b) 0,05м от дна выработки
Одним из параметров, характеризующих турбулентное течение, является кинетическая энергия турбулентности. На рисунке 4 показано сравнение измеренных и рассчитанных значений кинетической энергии турбулентности. Существует видимое качественное соответствие между численными и экспериментальными данными. Только на расстоянии 0,25м от входного отверстия и на высоте ¼ выработки расчетные значения кинетической энергии турбулентности значительно занижены. Средняя относительная погрешность между измеренными и рассчитанными значениями кинетической энергии турбулентности составляет 27% для модели RSM и 31% для стандартной модели k‐ε. Сравнение численных результатов с использованием моделей турбулентности: Raelizable k‐ε и SST k‐ω с экспериментальными данными было представлено в [10]. Средняя относительная погрешность между измеренной и рассчитанной величинами скорости составила около 30%, а средняя относительная погрешность между измеренной и рассчитанной кинетической энергией турбулентности составила 42% [10].
4. Рециркуляционный поток
На рисунке 5 показано поле скоростей в горизонтальной плоскости на высоте 0,05м над дном выработки, полученное в результате эксперимента и расчета. Представленная картина поля скоростей охватывает зону с рециркулирующими потоками. Из‐за используемой методики измерения область под каналом подачи воздуха была невидима для CCD‐камеры, следовательно, результаты измерений для этой области x∈[0,08м, 0,2 м] недоступны. Похоже, что прогнозируемый диапазон зоны с рециркуляционными потоками в направлении выходного отверстия завышен. Измеренная длина зоны рециркуляции потока в направлении выхода составляет почти 0,2м, а прогнозируемые значения составляют: 0,6 м для RSM и 2,2 м для модели k‐ε. На рис. 6 показано сравнение измеренной и прогнозируемой продольных составляющих вектора скорости вдоль линий, определенных координатами x∈[2,0м,0,08м], y=-0,1м и y=-0,35м и для z=0,02м (ось воздуховода) и для z=-0,05м (¼ высоты канала). В этой области течения расчетные значения продольных составляющих вектора скорости завышены. Это означает, что прогнозируемая объемная скорость воздушного потока в этой зоне также имеет тенденцию быть завышенной. В этом разделе результаты, полученные с помощью модели RSM, лучше приближены к данным измерений.
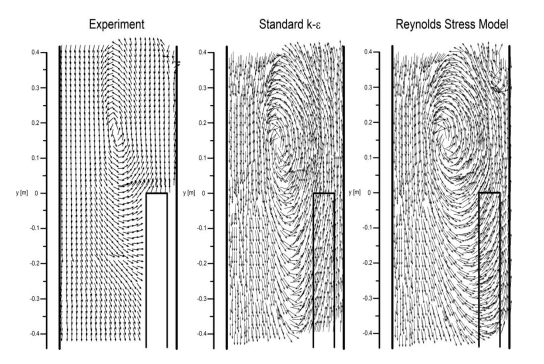
Рисунок 5. Поле скоростей в зоне рециркуляции в горизонтальной плоскости на высоте 0,05м над дном выработки. Сравнение численных и экспериментальных результатов
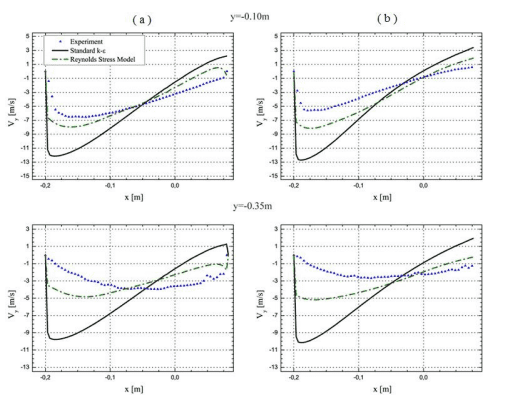
Рисунок 6. Распределение продольной составляющей скорости по горизонтальным линиям, на уровне слева - ось подводящего канала, справа - 0,05м от дна выработки
5. Сходство полей скоростей
Измерения проводились для трех средних скоростей входного воздушного потока: 15,4 м/с, 21,2 м/с и 35,4 м/с. Числа Рейнольдса, соответствующие этим скоростям, равны 78000, 108000 и 180000 соответственно. На рисунке 7 показаны распределения нормализованных величин вектора скорости для выбранных измерительных линий. Величина вектора скорости |
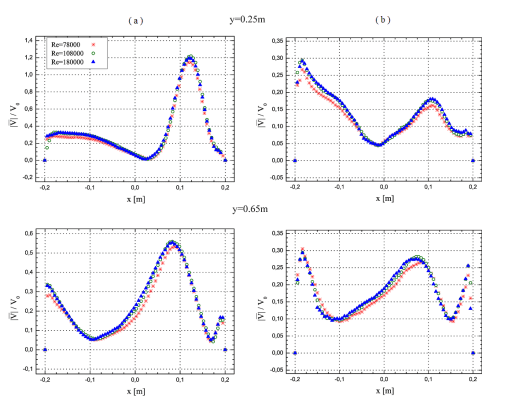
Рисунок 7. Нормированное распределение величины скорости по горизонтальным линиям на уровне: слева - ось подводящего канала, справа - 0,05м от дна выработки
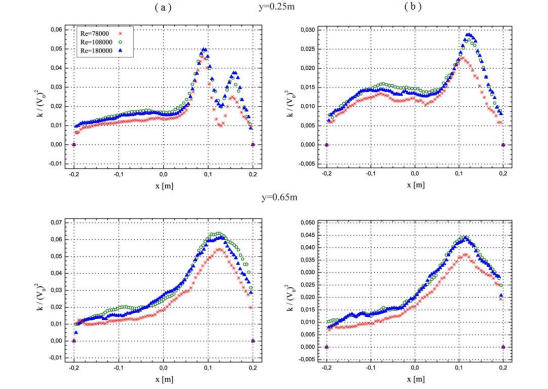
Рисунок 8. Нормированное распределение кинетической энергии турбулентности k по горизонтальным линиям на уровне: слева - ось подводящего канала, справа - 0,05м от дна выработки.
6. Выводы
При планировании вентиляции глухих выработок необходимо учитывать ряд факторов, к которым прежде всего относятся опасности метана и пыли. В настоящее время параметры воздушного потока часто определяются с использованием CFD‐подхода. Валидация модели турбулентности остается необходимым шагом в процессе проверки данных. В условиях добычи полезных ископаемых проверка результатов численного моделирования чрезвычайно затруднена из‐за условий окружающей среды (высокая влажность и концентрация пыли в воздухе) и возможностей измерений в сочетании с применимыми правилами техники безопасности. В качестве альтернативы измерения производятся на физических моделях. Представленные здесь сравнения показывают, что результаты, полученные с использованием обеих моделей турбулентности (k‐ε и RSM), отражают реальное поведение потока с одинаковой точностью. В качественном выражении прогнозируемое поле скоростей хорошо коррелирует с данными измерений. Средняя относительная погрешность между результатами расчетов и измерений величины вектора скорости и кинетической энергии турбулентности составляет около 29% для RSM и 33% для модели k‐ε. Расчетная дальность зоны рециркуляции в направлении выходного отверстия завышена. В этой зоне прогнозируемые значения продольных составляющих вектора скорости также завышены. Это означает, что фактическое количество рециркулирующего воздуха в этой зоне также завышено. Как измеренные, так и рассчитанные нормализованные (по средней скорости на входе) поля скорости, а также кинетическая энергия турбулентности качественно согласуются в диапазоне чисел Рейнольдса 100000÷200000. Исходя из этого, можно предположить, что ошибка в прогнозируемых значениях вектора скорости будет близка к оцененным также в случае больших чисел Рейнольдса.
1. Wala A M, Stoltz J R and Jacob J D 2001 Proc. 7th Int. Mine Ventilation Cong. Krakow 411
2. Wala A M, Vytla S, Taylor C D and Huang G 2007 Mine face ventilation: a comparison of CFD results against benchmark experiments for CFD code validation Mining Engineering 59 10
3. Szmyd J, Branny M, Karch M, Wodziak W, Jaszczur M and Nowak R 2013 Experimental and numerical analysis of the air flow in T-shape channel flow Arch. of Mining Sciences 58 333
4. Parra M T, Villafruela J M, Castro F and Mendez C 2006 Numerical and experimental analysis of different ventilation systems in deep mines Building and Environment 41 2 87
5. Sasmito A, Birgesson E, Ly H C and Mujumdar S 2013 Some approaches to improve ventilation system in underground coal mines environment – A computational fluid dynamic study Tunnelling and Underground Space Technology 34 82
6. Kurnia J C, Sasmito A P and Mujumdar A S 2014 Dust dispersion and management in underground mining faces Int. J. Mining Science and Technology 24 39
7. Kurnia J, Sasmito A and Mujumdar A 2014 Simulation of a novel intermittent ventilation system for underground Tunnelling and Underground Space Technology 42 206
8. Branny M, Karch M, Wodziak W, Jaszczur M, Nowak R and Szmyd J 2014 An experimental validation of a turbulence model for air flow in a mining chamber J. Phys. Conf. Series 530 012029
9. Branny M, Szmyd J, Jaszczur M, Nowak R, Filipek W and Wodziak W 2013 Model research of air flow in blind headings with fun and duct system of ventilation Gornictwo i Geologia 8 5 (in polish)
10. Wodziak W 2015 Experimental and numerical study of air flow in a laboratory model of blind channel aired by a force ventilation system PhD Thesis AGH University of Science and Technology Krakow (in polish)