Аннотация
Приведен анализ сырья строительных материалов на этапах сушки в барабанных сушилках с учетом количества конвективного тепла, проходящего через металлические части барабана во время сушки.
Введение
Интенсивное развитие строительной отрасли в нашей стране сопровождается резким увеличением спроса на стекольную продукцию, а также повышением требований к ее качеству. В результате это приводит к усилению конкуренции среди производителей и модернизации производственных процессов. Одним из способов снижения себестоимости продукции является оптимизация энергоемких процессов. Одним из таких процессов в стекольной промышленности является обработка сырья в сушильных барабанах. Большое количество энергии расходуется на испарение жидкости, содержащейся в сырье. Поэтому анализ режимов работы существующих сушильных барабанов, повышение энергоэффективности аппарата путем выбора оптимальных режимов процесса сушки является актуальной задачей.
Анализ теоретических описаний тепловых и метаболических процессов, а также методов исследования процессов сушки позволил разработать основы лабораторного оборудования, предложения по интенсификации и управлению процессами. Исследование тепловых и обменных процессов в сушильных барабанах позволяет полно осветить различные аспекты изменения характеристик и кинетики сушки, происходящей в аппарате. Для создания математической модели этого процесса, повышения температуры материала на стадиях сушки, циклов испарения несвязанной свободной и связанной влаги, равновесия сушильного агента с влажным материалом, тепла, получаемого от нагрева воздуха от конструктивных элементов барабана, необходимо учитывать дополнительное тепло, передаваемое материалу и перемешивание материала сушильного агента. Для этого необходимо рассмотреть процесс отдельно на каждой стадии сушки. На первой стадии сушки сушильный агент насыщен на поверхности материала, и испарение влаги с поверхности материала происходит по законам перехода свободной жидкости в парообразное состояние. В этом случае скорость процесса сушки определяется количеством теплоты, переданного от теплового сушильного агента путем конвекции к влажному материалу.
Объект и метод исследования
Известно, что в барабанной сушилке существует два вида теплообмена - контактный и конвективный способы. Однако большое количество тепла, передаваемого высушиваемому материалу, осуществляется конвективным теплообменом. Количество тепла, передаваемого конвективным способом высушиваемому материалу в барабанной сушилке, до 20 раз больше, чем количество тепла, передаваемого контактным способом. Интенсивность конвективной теплопередачи в барабанной сушилке, в свою очередь, напрямую связана с раскрытием поверхности частиц. Чем больше материал распространяется по поверхности барабана, тем больше площадь поверхности открытых частиц для конвективного теплообмена. Обобщая вышесказанное, мы видим, что эффективность сушки минеральных удобрений в барабанной сушилке существенно зависит от равномерности и поверхности завесы высушиваемого материала, падающего из сопел внутренних барабанных устройств. Обеспечение рассеивания поверхности частиц по сечению барабана является основным назначением внутренних устройств барабана (форсунок) [2].
На основании вышеизложенного, для интенсификации процесса сушки суперфосфатного удобрения и увеличения поверхностей теплообмена, была разработана конструктивная схема сопла, формирующего поверхности теплообмена, и создан лабораторный вариант сушилки [6]. На рисунке 1 показан общий вид экспериментального устройства.
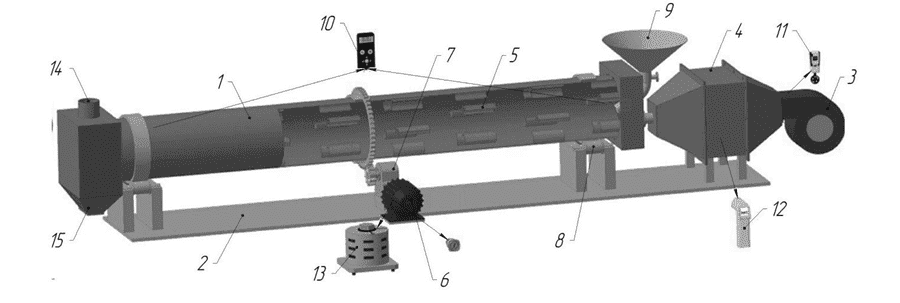
Рисунок 1 – Схема экспериментального устройства:
1 - корпус сушилки; 2 - пол; 3 - вентилятор; 4 - калорифер; 5 - сопло; 6 - электродвигатель; 7 - редуктор; 8 - опорные ролики; 9 - бункер; 10 - электронный манометр; 11 - анемометр; 12 -элкектронный термометр; 13 - ЛАТР; 14 - труба дымохода; 15 - бункер для разгрузки продуктов
Исследования проводились на экспериментальном устройстве для проверки адекватности предложенной модели реальному процессу сушки. Полученные результаты показали, что предложенная математическая модель согласуется с экспериментальными результатами.
Одним из важных параметров, определяющих скорость процесса в сушильном барабане, является температура сушильного агента. При непрерывной сушке, температура сушильного агента снижается по длине аппарата за счет теплопередачи к материалу, лопастям барабана и стенкам.
Во время испарения второй связанной влаги сушки на внешней поверхности материала образуются сухие участки, относительная влажность сушильного агента на поверхности материала внезапно уменьшается. В результате чего, повышается температура поверхности материала, значение которой рассчитывается по равновесию высушиваемого материала с сушильным агентом.
При горячей стенке барабана и лопаты, под воздействием тепла зерен материала, на его наружном слое образуется высушенная поверхность, причем ее размер и толщина увеличиваются по длине барабана. Высушенный материал по своей теплопроводности аналогичен горячеизоляционным материалам. В результате, основным сопротивлением процессу теплообмена является высушенная поверхность материала, где этот - же слой образует поверхность процесса теплообмена. Процессы, происходящие в этой зоне, определяются критерием Лыкова. При малых значениях числа Лыкова жидкость не успевает подняться к поверхности частицы во внутренних слоях материала, и на его внешней поверхности образуется слой сухого материала. Этот слой образуется между поверхностью теплообмена и поверхностью испарения.
На рис. 2 показана схема размещения материала при сушке. Материал, подлежащий сушке в барабанном аппарате, распыляется из верхней лопаты на дно или нижнюю часть барабана, а оставшийся материал остается застрявшим в лопатах. В зоне контакта на поверхности этого материала происходит теплообмен, и происходит процесс формирования частицы из внешнего слоя. До следующего вращения барабана все частицы этого слоя находятся в контакте с нагретыми элементами барабана. Поскольку это время контакта намного меньше общего времени нахождения материала в барабане, мы используем теорию кратковременного контакта для математического моделирования процесса теплообмена внутри слоя.
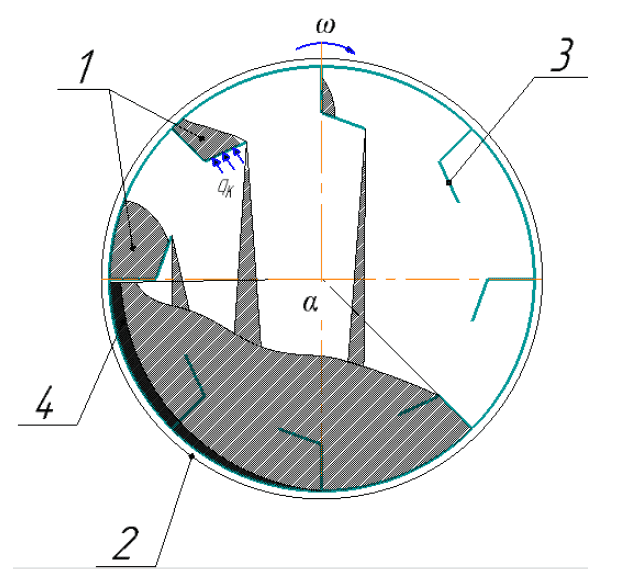
Рисунок 2 – Схема размещения материала при сушке:
1 - влажный материал; 2 - стенка барабана; 3 - лопаты; 4 - сухой материал
Помимо конвективной энергии, получаемой частицами от нагретого воздуха в процессе теплообмена в сушильном барабане, необходимо учитывать количество контактного тепла, получаемого частицами материала от металлических элементов аппарата. Принимая внешнюю форму высушиваемых частиц в виде прямой сферы, считаем, что количество дополнительного тепла, проходящего через металлические элементы аппарата, с точки зрения теплопроводности к частице равно Qk. В этом случае мы находим изменение величины Qk по закону Фюре из следующего уравнения:
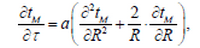
где: λм - теплопроводность материала; tм - температура материала; R - часть радиуса; S - поверхность; τ - время; G - колличество материала.
Чтобы определить градиент температуры на поверхности сферической частицы, необходимо знать изменение толщины частицы. Эта величина находится по дифференциальному уравнению теплопроводности:
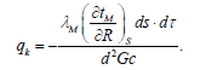
Начальным условием этого уравнения будет:
τ = 0 когда tм = const и τ > 0 когда tм = f (R) и граница условия: tмповерх. = tнасыщ. и (dtм⁄dR) = 0.
где R - частичный радиус; tмповерх. - температура поверхности материала, tнасыщ. - температура насыщения водяного пара при давлении внутри аппарата.
Это уравнение было решено численным методом решения дифференциальных уравнений. При анализе траектории движения частиц материала в сушильном барабане этот процесс можно сравнить с процессом молекулярной диффузии на основе анализа движений в структуре потока. Это сходство также было отмечено многими исследователями. Поэтому мы рассматриваем движение материала в сушильном барабане в соответствии с моделью диффузии и используем уравнения процессов молекулярной диффузии. Одним из таких параметров в свойстве массопереноса является коэффициент продольного перемешивания. Этот коэффициент аналогичен коэффициенту молекулярной диффузии. Рассчитывая аналогично процессы массопереноса и теплопереноса, мы предполагаем продольное перемешивание тепла коэффициент, аналогичный коэффициенту продольного перемешивания для процесса теплообмена.
Диффузионная модель теплопередачи в электродвижущей части аппаратной длины сушильного агента выглядит следующим образом:
Это уравнение дает дифференциальное представление об изменении температуры сушильного агента по длине аппарата за счет перемешивания. Для решения этого уравнения необходимо определить изменение температуры материала по длине аппарата во время сушки. Поэтому мы используем численные методы для решения этого дифференциального уравнения. При этом мы предполагаем, что физические свойства материала не изменяются на данном участке. Кроме того, поскольку изменение температуры и влажности сушильного агента на данном полученном участке невелико, мы считаем их линейную скорость изменения постоянной. Пройдем шаг за шагом численный метод решения уравнения. То есть в качестве граничных условий задается только начальная температура в начале сушки. Поэтому изменение температуры на каждом шаге сравнивалось с экспериментальными результатами, пока мы не достигнем желаемой точности. Метод решения этого численного дифференциального уравнения также может быть использован, когда мы получаем движение сушильного агента методом идеального сжатия.
Моделирование процесса сушки рассчитывается с одинаковым шагом для всех элементов барабана. В этом случае величина шага зависит от длины барабана и количества полученных элементов.
Список использованной литературы
1. Ахунбаев, А. А., Ражабова, Н. Р., и Вохидова, Н. Х. (2020). Исследование гидродинамики роторной сушилки с быстровращающимся ротором. Экономика и социум, (12-1), 392-396.
2. Тожиев, Р. Ж., Ахунбаев, А. А., & Миршарипов, Р. Х. (2018). Сушка тонкодисперсных материалов в безуносной роторно-барабанном аппарате. Научно-технический журнал ФерПИ,-Фергана, (2), 116-119.https://cyberleninka.ru/
3. Тожиев, Р. Ж., Ахунбаев, А. А., Миршарипов, Р. Х., Муллажонова, М. М. К., и Йигиталиев, М. М. У. (2021). Анализ процесса сушки минеральных удобрений в барабанном аппарате. Universum: технические науки, (8-1 (89)), 31-36.
4. Миршарипов, Р. Х., и Ахунбаев, А. А. (2020). Исследование гидродинамических параметров барабанной сушилки. Международный журнал передовых исследований в области науки, техники и технологии, 7(11).
5. Тожиев, Р. Ж., Миршарипов, Р. Х., Ахунбаев, А. А., и Абдусаломова, Н. А. К. (2020). Оптимизация конструкции сушильного барабана на основе системного анализа процесса. Universum: технические науки, (11-1 (80)).
6. Тожиев, Р. Ж., Миршарипов, Р. Х., Ахунбаев, А. А., и Абдусаломова, Н. А. К. (2020). Оптимизация конструкции сушильного барабана на основе системного анализа процесса. Universum: технические науки, (11-1 (80)).https://7universum.com/
7. ВЫСУШИВАНИЕ ДИСПЕРСНЫХ МАТЕРИАЛОВ В АППАРАТЕ С БЫСТРО ВРАЩАЮЩИМСЯ РОТОРОМ. Universum: технические науки, (7-1 (88)), 49-52.
8. Тоджиев, Р. Ж., Ахунбаев, А. А., и Миршарипов, Р. X. (2021). ИССЛЕДОВАНИЕ ГИДРОДИНАМИЧЕСКИХ ПРОЦЕССОВ ПРИ СУШКЕ МИНЕРАЛЬНЫХ УДОБРЕНИЙ В БАРАБАННЫЕ СУШИЛКИ. Научно-технический журнал, 4(4), 10-16
9. Тожиев, Р. Ж., Ахунбаев, А. А., Миршарипов, Р. Х., Муллажонова, М. М. К., и Йигиталиев, М. М. У. (2021). Анализ процесса сушки минеральных удобрений в барабанном аппарате. Universum: технические науки, (8-1 (89)), 31-36.
10.Тожиев, Р. Ж., Ахунбаев, А. А., Миршарипов, Р. Х., Муллажонова, М. М. К., и Йигиталиев, М. М. У. (2021). Анализ процесса сушки минеральных удобрений в барабанном аппарате. Universum: технические науки, (8-1 (89)), 31-36.
11.Тожиев, Р. Ж., Миршарипов, Р. Х., Ахунбаев, А. А., и Абдусаломова, Н. А. К. (2020). Оптимизация конструкции сушильного барабана на основе системного анализа процесса. Universum: технические науки, (11-1 (80)).
12.Ахунбаев, А. А., Ражабова, Н. Р., и Вохидова, Н. Х. (2020). Исследование гидродинамики роторной сушилки с быстровращающимся ротором. Экономика и социум, (12-1), 392-396.
13.Ализафаров, Б. М. (2020). ЭКОЛОГИЧЕСКАЯ СУШКА МЕЛКОДИСПЕРСНЫХ МАТЕРИАЛОВ В КОНТАКТНОЙ СУШИЛКЕ. Экономика и социум, (11), 433-437.
14.Расулжон, Т., Акмалжон, А., и Ильхомжон, М. (2021). ВЫБОР ФИЛЬТРУЮЩЕГО МАТЕРИАЛА И АНАЛИЗ РАСЧЕТНЫХ УРАВНЕНИЙ ПРОЦЕССА МАССООБМЕНА В РОТОРНОМ ФИЛЬТРУЮЩЕМ АППАРАТЕ. Универсум:технические науки, (5-6 (86)), 22-25.
15.Исомиддинов, А., Аксроров, А., Каримов, И., и Тоджиев, Р. (2019). Применение роторно-фильтрового очистителя запыленного газа в промышленности и определение его эффективности. Австрийский журнал технических и естественных наук, (9-10).
16.Тожиев, Р. Ж., Ахунбаев, А. А., & Миршарипов, Р. Х. (2018). Сушка тонкодисперсных материалов в безуносной роторно-барабанном аппарате. Научно-технический журнал ФерПИ,-Фергана, (2), 116-119