Система автоматического определения габаритов груза
Автор: К. А. Солодухин, А. В. Хорхордин
Источник: Сборник научных трудов конференции Автоматизация технологических объектов и процессов. Поиск молодых
, Донецк: ДонНТУ, 2022. - с. 222-226.
Вступление
Определение размеров посылок в последнее время становится критически важным для отраслей электронной коммерции и логистики, поскольку они напрямую связаны с оптимизацией пространства и ценообразования по доставке грузов.
Существуют различные разработки, позволяющие автоматизировать процесс измерения габаритов грузов. Чаще всего груз необходимо разместить в области измерения в складской зоне, после чего процесс сканирования выполняется автоматически с передачей результатов в учетную систему. Крупные компании полагаются на автоматизированные решения определения размеров, позволяющих избежать трудоемких и часто неточных ручных измерений, сэкономить драгоценное пространство и снизить затраты [1].
Так, например, в 2014 году система почтовых отправлений в России испытала коллапс, связанный с увеличением посылок из Китая. В связи с этим ФГУП «Почта России» приняло решение о проведении глобальной модернизации крупнейшего в Европе сортировочного узла почтовых отправлений «Логистический центр «Внуково». В рамках выполнения работ по модернизации конвейерно-сортировочных линий была поставлена задача оснащения узлов сортировки системой машинного (технического) зрения [2].
Постановка задачи
С целью повышения производительности, увеличения скорости обработки грузопотока и уменьшения ошибок необходимо разработать автоматическую систему измерения (САИ) габаритов объектов аморфных форм путём внедрения системы компьютерного зрения. САИ должна определять габариты груза по результатам обработки видеоизображения, получаемого с типовой видеокамеры (веб-камеры, фото или видео). Положение груза под видеокамерой – произвольное (не строго ориентированное). С целью обеспечения невысокой стоимости для технической реализации САИ габаритов грузов использовать одноплатную ЦВМ типа RaspberryPi и программное обеспечение типа OpenCV.
Анализ решений и разработка концепции построения системы
САИ габаритов грузов различаются по размерам измеряемых грузов, пропускной способности, вариантам монтажа; они могут измерять груз в статике или в динамике в процессе движения груза по конвейеру. Потенциальными заказчиками САИ габаритов являются логистические и транспортные компании, распределительные центры, дистрибьюторы и производители негабаритного товара. Существующие САИ в основном используют ультразвуковые и/или инфракрасные датчики.
Ультразвуковые САИ хорошо подходят для измерения внешних границ упаковки. Они обнаруживают объекты независимо от их оптических свойств. Точность измерения не зависит от цвета объекта или наличия отражающих поверхностей, поскольку они не влияют на распространение и отражение звуковых волн. Это обеспечивает надёжное распознавание упаковок, даже если они обёрнуты, например, глянцевой плёнкой или целлофаном.
Инфракрасные САИ представлены зачастую большим количеством инфракрасных датчиков для определения пространственных координат предметов, проходящих в рамке между двумя оптическими шторками (инфракрасными барьерами).
Хорошо прослеживается тенденция к созданию САИ габаритов на основе систем технического зрения (СТЗ). Основным элементом таких систем являются камеры глубины, создающие изображение, в каждом пикселе которого хранится помимо цвета расстояние до объекта. СТЗ предоставляет информацию об объекте в виде облака точек. Каждая точка облака – это расстояние до объекта и набор вершин в трёхмерной системе координат [3].
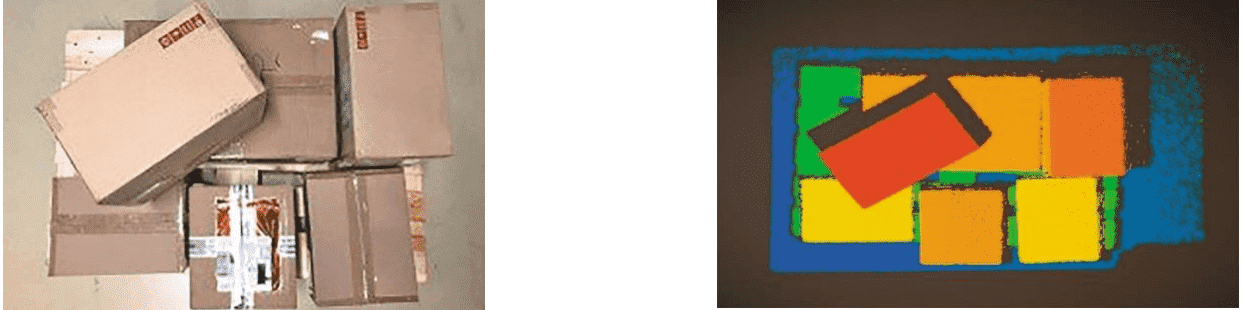
Рисунок 1 – а) Реальное изображение, б) Изображение, полученное с помощью камер глубины
Описание алгоритма работы разрабатываемой системы
Основной принцип работы СТЗ – получение нескольких снимков одной и той же сцены с разных ракурсов (одной или несколькими видеокамерами), сопоставление снимков и вычисление трёхмерных координат точек сцены. Изображение объекта создается по методу, суть которого заключается в использовании видеокамеры и двух зеркал, расположенных под определенными углами относительно ее оптической оси. Зеркала обеспечивают захват камерой изображения, состоящего из стереопары, так что на выходе получают одно изображение, несущее информацию об объекте. Далее его разделяют на правую и левую части, после чего каждую часть можно использовать для получения карты глубин.
Построение карты глубины иллюстрирует рис. 3. Точка Y – некоторая точка наблюдаемого объекта, X1 и X2 – проекции точки Y на плоскостях a и b (изображениями с зеркала 1 и зеркала 2 соответственно). Отрезки d1 и d2 являются расстояниями, измеряемыми в пикселях от начала координат горизонтальной оси до точек X1 и X2 соответственно. Ввиду того что зеркала расположены под разными углами к видеокамере, расстояния d1 и d2 на изображениях стереопары различается на некоторую величину, называемой диспаратностью. При нахождении объекта в непосредственной близости от камеры значение диспаратности точки Y будет наибольшим, а по мере удаления объекта оно будет уменьшаться [4].
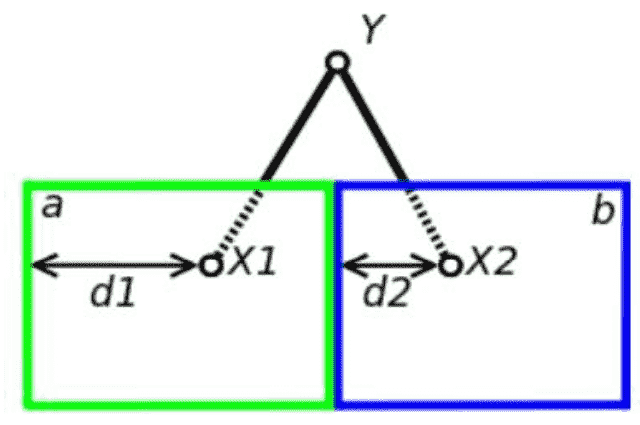
Рисунок 2 – Нахождение диспаратности
Для настройки СТЗ необходимо выполнение следующих видов работы:
- Центровка видеокамеры. Позволяет настроить положение камеры в пространстве относительно зеркал, после чего ее необходимо зафиксировать.
- Исключение зоны нечеткости на изображении. Позволяет выделить область нечеткости, образованную стыком зеркал и сохраняет параметры этой области, для последующей нарезки изображений.
- Захват и сохранение калибровочных изображений. На данном этапе производится получение N–снимков калибровочного шаблона
шахматная доска
и сохранение их в указанную директорию. - Нарезка калибровочных изображений по параметрам, сохраненным на шаге 2.
- Калибровка стереопары. Калибровка необходима для устранения искажений вносимыми оптическим трактом видеокамеры, для корректной работы программы построения карты глубин. Калибровка производится алгоритмами библиотеки OpenCV, после чего происходит сохранение ее параметров. С помощью этих параметров можно производить ректификацию изображений стереопары, то есть воспроизводить их без искажений.
- Настройка карты глубины производится вручную, изменением различных параметров. По достижению оптимальных параметров карты глубины, они сохраняются для использования во втором этапе работы системы. При выбранных настройках карты глубин диспаратность вычисляется для особых точек наблюдаемого объекта, таких как контуры.
После настройки СТЗ и САИ габаритов работают по следующему алгоритму:
- захват изображения со стереопары;
- получение стереопары захваченного изображения;
- ректификация изображения стереопары;
- построение карты глубины, причем, чем ближе наблюдаемая грань объекта к
видеокамере, тем выше интенсивность цвета его контура;
- вычисление расстояния до наблюдаемого объекта и формирование контура объекта;
- вычисление геометрических размеров объекта.
Синтез системы технического зрения
Камеры описываются с помощью следующей модели, называемой проективной камерой. Проективная камера определяется центром камеры, главной осью – лучом, начинающимся в центре камеры и направленным туда, куда камера смотрит, плоскостью изображения – плоскостью, на которую выполняется проецирование точек, и системой координат на этой плоскости. В такой модели произвольная точка пространства X проецируется на плоскость изображения в точку x, лежащую на отрезке CX, который соединяет центр камеры C с исходной точкой X (рис. 3).
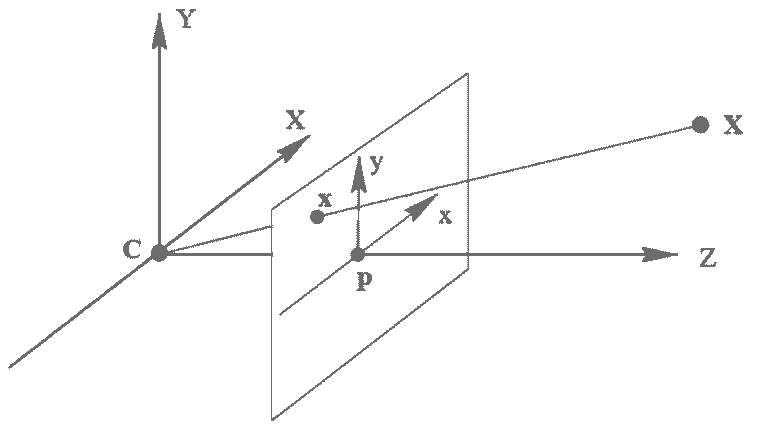
Рисунок 3 – Модель камеры. C – центр камеры, Cp – главная ось камеры.
Формула проецирования, записанная в однородных координатах:
где X – координаты точки в однородной системе координат;
x – координаты точки, находящейся в плоскости изображения, в однородной системе
координат;
P – фотоматрица или матрица камеры, заданного размера 3×4.
Построим матрицу P используя следующее выражение:
где K – квадратная матрица, размера 3х3 имеющая все ненулевые элементы выше главной
диагонали;
R – матрица поворота, которая ортогональна K, определяющая поворот камеры
относительно глобальной системы координат;
I – единичная матрица соответствующих размеров;
C – вектор, определяющий центр камеры, в нашем случае, центр камеры совпадает с
началом системы координат;
t = RC.
Матрица камеры определена с точностью до некоторой константы, отличной от нуля, более того результаты проецирования точек по формуле (1) инвариантен относительно этой константы.
Поместим центр камеры в начало координат. В таком случае, главная ось камеры совпадёт с осью Сz, более того, предположим, что оси координат, расположенные на плоскости изображения имеют одинаковый масштаб, а центр изображения имеет нулевые координаты, т.е. координаты центра изображения, учитывая эти допущения, матрица камеры будет иметь вид:
Как правило, у реальных камер пиксели слегка отличны от квадратных. А центр изображения смещён, т.е. имеет ненулевые координаты. Принимая это во внимание, перепишем матрицу внутренних параметров камеры следующим образом:

где αx, αy – фокусное расстояние камеры вдоль осей x, y.
В действительности, оптика не идеальна, часто коэффициент линейного увеличения не постоянен, по мере удаления от главной оси камеры он может меняться, это приводит к тому, что на изображениях появляются искажения – дисторсии. Данные искажения учитываются следующей нелинейной математической моделью:
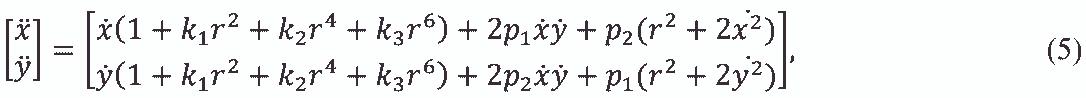
где k1, k2, k3, p1, p2 – коэффициенты дисторсии, являющиеся параметрами оптической
системы.
(x′, y′) – координаты точек на плоскости проекции относительно центра изображения
при учёте что пиксели квадратные, а в оптической системе отсутствуют искажения;
(x, y) – координаты точек на плоскости проекции относительно центра изображения,
затронутые оптическими искажениями, при учёте что пиксели квадратные.
Допустим, что имеется пара откалиброванных камер, т.е. камер заданных со своими матрицами, и пусть x –однородные координаты точки на плоскости изображения одной камеры, а x′ – на плоскости изображения другой. Напомним, что существует матрица F размера 3×3, такая что пара точек x, x′ является стереопарой тогда и только тогда, когда:
В таком случае F называется фундаментальной матрицей. Её ранг будет равен 2, она определена с точностью до ненулевого множителя и инвариантна относительно точек x, x′, т.е. зависит только от исходных матриц P и P′.
В случае, когда матрицы P и P′ имеют вид (2) и (3), фундаментальная матрица может быть вычислена по формуле (7).
С помощью фундаментальной матрицы можно получить уравнения эпиполярных линий. Для точки x вектор, задающий эпиполярную линию, будет иметь вид l′ = Fx, а уравнение самой эпиполярной линии: l′x′ = 0. Аналогично, для точки x′ вектор, задающий эпиполярную линию, будет иметь вид l = Fx′.
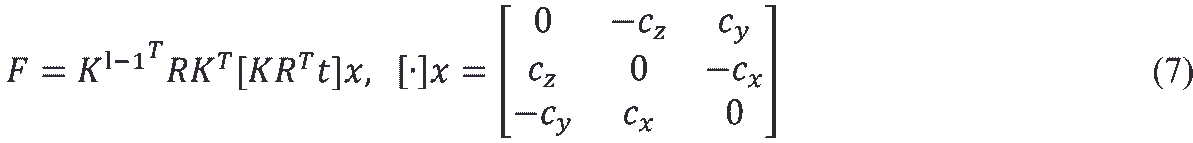
Пусть имеются две камеры с матрицами P1 и P2. x1 и x2 – однородные координаты проекций некоторой точки пространства X. Составим следующую систему:

Решим эту систему, и построим карты глубины с помощью приёмов, представленных в [4]. Парные точки будем искать на эпиполярных линиях. Чтобы упростить поиск, выровняем изображения, относительно эпиполярных линий, так чтобы они были параллельны сторонам изображения. Этот процесс выравнивания изображений называется ректификацией. После проделанной ректификации выполним поиск соответствующих пар точек. Самый простой способ показан на рис. 5. Для каждого пикселя левой картинки с координатами (x0, y0) выполняется поиск пикселя на правой картинке. При этом предполагается, что пиксель на правой картинке должен иметь координаты (x0-d, y0), где d - величина, называемая несоответствие/смещение.
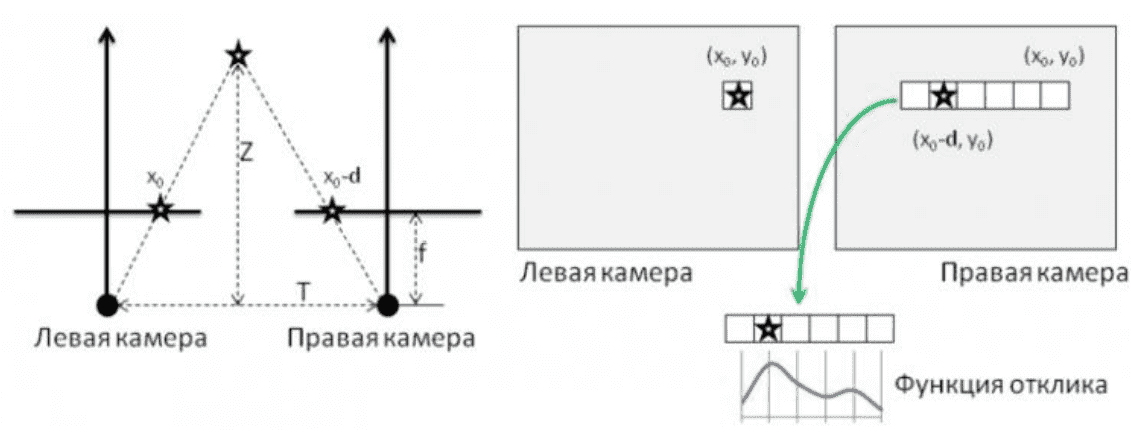
Значения глубины обратно пропорциональны величине смещения пикселей. Если использовать обозначения с левой половины рис. 5, то зависимость между смещением и глубиной можно выразить следующим способом (9):

Вывод
В настоящее время на рынке систем автоматического измерения габаритов широко используются системы, использующие аппаратные средства измерения. Использование видеокамер увеличивает пределы измерений, и при корректной разработке необходимых алгоритмов появляется возможность измерять габариты грузов сложной формы. Интеллектуальные алгоритмы всё больше находят своё применения в разных технических решениях, и их применение для определения габаритов грузов представляется многообещающим и успешным решением.
Перечень ссылок:
- Чемидов, И. В. АСУ складским комплексом как элемент единого информационного пространства приборостроительного предприятия / И. В. Чемидов, Д. В. Капулин, М. А Казанцев, Н. Н. Джиоева // Автоматизация в промышленности. – М.: Инфоавтоматизация, 2016. – №11. – С.27–30
- Фадкин А.В. Интеграция системы SCADA и системы машинного зрения в автоматизированных системах управления логистического центра ФГУП «ПОЧТА РОССИИ». Новые технологии в научных исследованиях, проектировании, управлении, производстве. Воронеж, 2017.
- Control Engineering Россия - Август 2021. Электронный доступ: https://controleng.ru/wp-content/uploads/9452.pdf (Дата обращения: 05.11.2021).
- Степанов, Д.Н. Математические модели получения стереоизображений с двухзеркальных катадиоптрических систем с учётом дисторсии объективов / Д.Н. Степанов // Компьютерная оптика. – 2019. – Т.43, № 1. – С. 105-114. – DOI: 10.18287/2412-6179-2019- 43-1-105-114