Аннотация

Продемонстрирован недорогой и компактный демодулятор FBG, для которого реализован высокоэффективный метод детектирования пиков. В качестве источника света используется недорогой перестраиваемый лазер, поэтому громоздкое и зачастую дорогостоящее устройство рассеивания света не требуется. Для сбора данных и обнаружения пика используется недорогая и компактная встраиваемая ARM-система STM32F4. Для определения длины волны пика был разработан высокоэффективный метод подгонки гауссовой кривой на основе алгоритма Левенберга-Марквардта (LM). Время демодуляции составляет всего 70 мс. Погрешность обнаружения пика составляет 0,87 пм при упоре настройки 10 пм. Он подходит для использования в полевых условиях, где требуется измерение в реальном времени.

Ключевые слова: датчик; встраиваемая система; алгоритм Левенберга-Марквардта (LM); подгонка данных; волоконная брэгговская решетка (FBG).

1. Введение

Датчики на основе волоконных брэгговских решеток (FBG) уже много лет успешно используются в качестве чувствительных элементов для измерения деформации, температуры, давления и т.д. благодаря присущим им преимуществам, таким как высокая точность, устойчивость к электромагнитным помехам и высокая надежность в жестких условиях эксплуатации. Принцип работы FBG основан на смещении центральной длины волны спектра отражения в результате изменения физических величин окружающей среды, таких как деформация, температура или давление [1,2]. Величина сдвига определяется обнаружением пика в системе демодуляции, поэтому алгоритм обнаружения пика играет важную роль в системе FBG-датчиков.

важную роль в системе FBG-датчиков. Существует множество алгоритмов обнаружения пиков, таких как дифференциальный метод, метод центроида, метод кросс-корреляции, метод Гаусса. Из всех вышеперечисленных методов, метод гауссовой подгонки имеет преимущество в высокой точности обнаружения пиков [3].

В традиционных системах демодуляции FGB часто используется широкополосный источник света и OSA, а также персональный компьютер для обнаружения пиковых длин волн. Это часто делает все системы громоздкими и дорогими. Для решения этой проблемы в данной работе разработана недорогая и компактная система демодуляции.

Для обнаружения пиковой длины волны был разработан высокоэффективный метод подгонки гауссовой кривой на основе алгоритма Левенберга-Марквардта (LM) [4]. Погрешность обнаружения пика составляет 0,87 пм, а время демодуляции - всего 70 мс.

2. Конфигурация оборудования

Аппаратная конфигурация показана на рисунке 1. В качестве источника света используется перестраиваемый лазер с шагом перестройки 10 пм. Лазер может сканировать всю полосу C с шагом 10 пм в течение менее 300 миллисекунд. Отраженный свет направляется в фотодетектор без элементов оптической дисперсии. Обнаруженный электрический сигнал подключается к встраиваемой компьютерной системе STM32F4 и преобразуется в цифровой сигнал с помощью встроенного в систему АЦП. Затем STM32F4 считывает данные и определяет пик с помощью подгонки кривой Гаусса.

В качестве источника света используется недорогой перестраиваемый лазер, поэтому громоздкое и часто дорогое устройство рассеивания света не требуется. Встраиваемая ARM-система STM32F4 используется для получения данных и обнаружения пика [5]. Преимуществами системы STM32F4 являются простота конструкции, высокая скорость, низкая стоимость и небольшой размер, поэтому нет необходимости в использовании громоздкого и дорогостоящего персонального компьютера.

Рис. 1 Схематическая диаграмма системы

Система STM32F4 также может взаимодействовать с главным компьютером через сетевой порт, порт USB, поэтому исходные данные и результат обнаружения пика могут быть отправлены на другой компьютер через эти порты для дальнейшей обработки.

3. Подгонка кривых

Для подгонки гауссовой кривой используется алгоритм Левенберга-Марквардта (LM). Алгоритм LM был предложен Левенбергом после инспирации Марквардтом. Алгоритм LM представляет собой комбинацию метода Ньютона и метода крутого спуска, который обладает высокой скоростью итераций и точностью подгонки. Алгоритм LM является стандартом для решения задачи нелинейных наименьших квадратов [6].

Алгоритм LM реализован на STM32F4 с использованием языка программирования C. Алгоритм может подгонять как одиночные пики, так и многопиковые. Подгонка выполняется очень быстро, требуется всего около 70 мс, что намного меньше времени сканирования данных.

4. Результаты и анализ

Сначала был подключен только один FBG. Исходные данные и подогнанная кривая показаны на рисунке 2. Было проведено 10 измерений, и погрешность пиковой длины волны составила 0,87 pm.

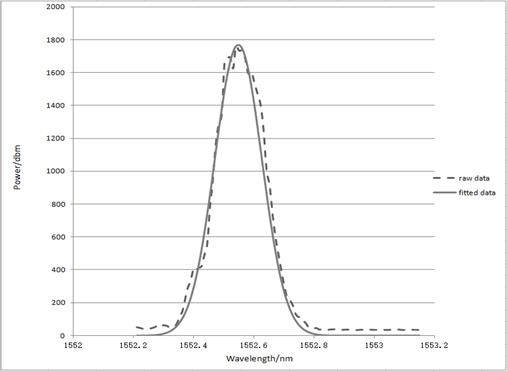
Рис. 2 Данные для одной длины волны

Затем были подключены три FBG для проверки возможности обнаружения нескольких пиков. Результат подгонки показан на рисунке 3.

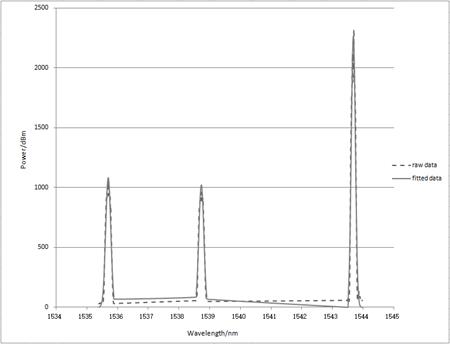
Рис. 3 Многоволновые данные, подогнанные по длине

Погрешность примерно такая же, как и для одной длины волны. Для подгонки трех пиков требуется около 70 мс. Подгонка одиночных пиков происходит гораздо быстрее. Время подгонки намного меньше времени получения данных, составляющего около 300 мс. Подгонка и сбор данных запрограммированы на параллельную работу, поэтому общее время одного измерения составляет около 300 мс. Таким образом, вся система отвечает требованиям обработки данных в реальном времени.

5. Вывод

В этой статье демонстрируется недорогой и компактный демодулятор FBG. В качестве источника света используется перестраиваемый лазер. Отраженный спектр может быть измерен непосредственно для каждой длины волны без использования диспергирующего элемента. Для получения и обработки данных используется встраиваемая компьютерная система STM32F4. Система компактна и недорогая, так как не требует громоздкого и дорогостоящего оптического диспергирующего элемента и персонального компьютера. Быстрая подгонка гауссовой кривой по алгоритму LM была реализована в STM32F4 с помощью языка программирования c. Погрешность обнаруженного пика длины волны составляет 0,87 пм, а время, необходимое для обнаружения пика, составляет всего 70 мс.

Источники

[1] A. D. Kersey, M. A. Davis, H. J. Patrick, M. LeBlance, K.

P. Koo, C. G. Askins, M. A. Putnam, and E. J. Friebele,” Fiber grating sensors,” J. Lightwave Technol. Vol. 15, pp. 1442-1463, 1997.

[2] K. O. Hill and G. Meltz, “Fiber Bragg grating technology: fundamentals and overview,” J. Lightwave Technol. Vol. 15,

pp. 1263-1276, 1997.

[3] Yongqian Li, Yang Xie, Guozhen Yao, Comparison of Peak Searching Algorithms for Wavelength Demodulation in Fiber Bragg Grating Sensors, Information Engineering and Computer Science (ICIECS), 2010 2nd International Conference on, pp. 1-4, 2010.

[4] Lourakis Manolis I. A., Argyros Antonis A.SBA. A Software Package for Generic Sparse Bundle Adjustment, Acm Transactions on Mathematical Softwave, vol. 36, no. 1,

pp. 2, 2009.

[5] Li Dapeng, Cao Guohua, Chen Jiyan, Research of Array CCD Imaging System Based on STM32F4, Advances in Education Research, vol. 30, pp. 79-84, 2013.

[6] Elliott David, Johnston Barbara M., Johnston Peter R. The method of steepest descent for estimating quadrature errors. Journal of Computational and Applied Mathematics, vol. 303,pp. 93-104, 2016.