Методы оценки влияния несинусоидальности напряжения на конденсаторные установки в системах электроснабжения

Аннотация

Рассмотрены задачи оценки ЭМС конденсаторных установок (КУ) в системах электроснабжения. Найдено допустимое значение несинусоидальной составляющей тока КУ, соответствующее действующим стандартам.

Общая постановка проблемы

Конденсаторные установки (КУ) широко применяются в системах электроснабжения для компенсации реактивной мощности, понятие которой относится к стандартной частоте 50 Гц (первая гармоника) [1]. Несинусоидальность напряжения приводит к перегрузке КУ. В связи с этим в ПУЭ [2, п.5.6.18] помимо токовой отсечки предусматривается дополнительная максимальная токовая защита (МТЗ) с уставкой 130 % номинального тока. Это требование относится к периодической несинусоидальной помехе электромагнитной совместимости (ЭМС), которая представляется рядом Фурье с неизменными действующими значениями гармоник. В действующих сетях такой частный случай встречается далеко не всегда, поэтому требуется разработать метод оценки ЭМС для случайных несинусоидальных процессов. Мощные электроприёмники в сети электроснабжения могут создавать периодические или случайные импульсные помехи. Поэтому актуальной является задача оценки их влияния на КУ. Для её решения необходимо составить схему замещения цепи «источник питания – КУ», а не только самой КУ, как это было принято до сих пор [3, 4 и др.].

Несинусоидальные помехи

Процесс изменения во времени t действующих значений напряжения U представляет собой сумму синусоидальной и несинусоидальной составляющих:

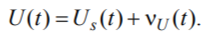
В ГОСТ 32144-2013 и EN 50160:2010 под синусоидальной (основной) составляющей понимается первая гармоника U1(t), что обусловлено использованием математической модели процесса (1) в виде ряда Фурье, когда уменьшение несинусоидальности осуществляется фильтрами высшего порядка n > 1.

Рассмотрим вначале периодические помехи. В ГОСТ 32144-2013 и EN 50160:2010 нормируются коэффициенты гармонических составляющих напряжения

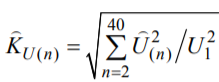
где действующие значения U(n) высших гармоник выражены в процентах U1. В ГОСТ 32144-2013 дополнительно нормируются их суммарные коэффициенты

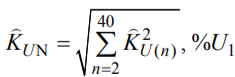
Здесь в обозначения из ГОСТ добавлен индекс ?.

Показатели (2) и (3) непосредственно не оценивают ЭМС, поскольку не учитывают зависимости действующих значений I(n) высших гармоник тока от частоты. В процентах номинального тока Iн КУ суммарный коэффициент несинусоидального тока

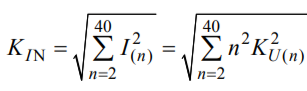
Периодический процесс изменения тока

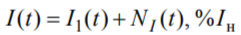
кроме основной составляющей содержит также несинусоидальную составляющую NI(t).

Для оценки нагрева проводников и электрооборудования используется математическая модель процесса изменения температуры в виде дифференциального уравнения первого порядка, правая часть которого пропорциональна квадрату тока [5, 6]. Постоянная времени нагрева КУ исчисляется часами [3, п. 50], поэтому температура перегрева будет практически пропорциональна квадрату эффективного тока:

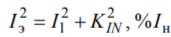
Длительность усреднения 10 мин (ГОСТ 32144-2013) и выдержка времени защиты не влияют на результаты расчётов.

При нормировании помехи ЭМС рассматриваются раздельно. Так, требования ПУЭ к релейной защите [2, п.п. 5.6.17, 5.6.18] выражаются в процентах от номинальных значений Uн напряжения и Iн тока, которые относятся к частоте 50 Гц. Подключение КУ может изменить напряжение от Uн до максимального значения Um ? 1,1 Uн, т.е. от 100 до 110 %. Такие же пределы будут и для тока. В нормировании основная составляющая напряжения, а следовательно, и тока принимается равной 100 %.

В ПУЭ значение 130 % относится к полному току. Допустимые значения помехи найдём из условия равенства эффективного значения норме:

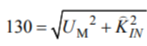
из которого найдем предельные значения KIN от 83,0 до 69,0 %. При превышении этих значений релейная защита будет отключать КУ.

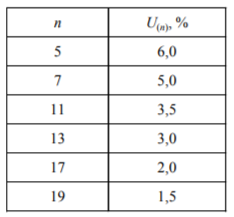
В НТП ЭПП-94 (п. 10.3.7) обоснование необходимости уменьшения токов и напряжений высших гармоник даётся из условия выполнения требований ГОСТ только по напряжению гармоник. Однако эти условные нормы нельзя относить к какому-то конкретному объекту, тем более к КУ. Поэтому они отнюдь не гарантируют, что КУ не будет недопустимо перегреваться. Например, пусть при Uн=0,38 кВ имеется шесть нечётных гармоник напряжения с действующими значениями, равными допустимым (табл. 1). Расчёт даёт значение KIN=84,2>83 %. Нормы по напряжению выполняются, но КУ будет отключена защитой. Противоположный пример: имеется одна пятая гармоника напряжения величиной 8 %, превышающая норму 6 %. В этом случае эффективное значение тока 107,7 % меньше 130 %. Здесь использование норм [3] приводит к ошибочному выводу о невозможности работы КУ.

Таблица 1

Перейдем к процессам с непериодической несинусоидальностью. Здесь требуется учитывать выдержку времени tРЗ релейной защиты, которая в ПУЭ [2, п. 5.6.18] не указывается. В проектировании она берется в пределах от 9 до 10 с [7, п.2.109]. В ГОСТ 1282-88 для приёмносдаточных испытаний КУ указано значение 10 с.

В качестве экспертной оценки примем значение 10 с, которое является длительностью квадратичного усреднения рассматриваемых процессов.

Исходным для расчётов является случайный процесс U(t). По некоторой аналогии с ГОСТ 30804.4.30 предлагается следующий алгоритм его получения. Ось времени разбивается на участки длительностью 0,2 с (10 циклов tц1=0,02 с). Для каждого участка вычисляются действующие значения всех гармоник напряжения порядка от 1 до 40. По ним, в отличие от [2], определяются действующие значения гармоник тока КУ. В пределах 10 с тот или иной процесс представляет собой решетчатую функцию с шагом дискретизации 0,2 с при количестве ординат 500. Не останавливаясь на особенностях статистической обработки случайных процессов разного вида, для краткости ограничимся рассмотрением эргодических процессов, у которых длительность интервала 40?k<10 c, где ?k ? время корреляции. В этом случае достаточно брать одну реализацию, а не их ансамбль.

По действующим значениям всех гармоник вычисляются ординаты решётчатой функции тока, которая в отличие от периодических процессов является случайной. Обычно расчётный эффективный десятиминутный максимум определяется с интегральной вероятностью 0,95. Электромагнитная совместимость обеспечивается, если он не превышает 130 %.

Выводы

При наличии несинусоидальности напряжения оценку перегрева КУ следует выполнять по эффективному значению тока синусоидальной составляющей помехи, с вероятностью превышения 0,05. При общей допускаемой токовой нагрузке 130 % доля несинусоидальной помехи составляет 83 % номинального тока КУ.

Список использованной литературы

1. Дрехслер Р. Измерение и оценка качества электроэнергии при несимметричной и нелинейной нагрузке. М.: Энергоатомиздат, 1985. 112 с.
2. Правила устройства электроустановок. Все действующие разделы шестого и седьмого изданий с изменениями и дополнениями на 1 февраля 2015. М.: Кнорус, 2015. 488 с.
3. Принцип оценивания и нормирования электромагнитной совместимости / Э.Г. Куренный, Е.Н. Дмитриева, А.П. Лютый, А.А. Булгаков // Электричество. 2016. № 1. С. 12 – 20.
4. Куренный Э.Г., Дмитриева Е.Н., Булг аков А.А. Статистическое решение задачи о квадратичном инерционном сглаживании случайных электроэнергетических процессов // Изв. РАН. Энергетика. 2016. № 4. С. 109 – 122.