Аннотация
Традиционные исследования дробильного эффекта двухзубчатой роликовой дробилки и плавности процесса дробления обычно учитывают один фактор. Но процесс дробления двухзубчатой роликовой дробилки является сложным процессом, поэтому существуют некоторые ограничения для учета влияния одного фактора. С помощью ортогонального эксперимента при имитационном анализе учитываются факторы влияния расстояния между роликами, скорости вращения и угла наклона. Получена наилучшая схема испытаний и порядок трех влияющих факторов, которые служат основой для проектирования двухзубчатой роликовой дробилки.
Введение
С быстрым развитием социальной экономики масштабы производства металлургии, добычи руды, транспорта, производства строительных материалов и других инфраструктурных отраслей растут, эти отрасли, как правило, используют большой объем сырья. Для изучения гранулометрического состава двухзубчатой роликовой дробилки необходимо изучить различный эффект дробления и стабильность двухзубчатой роликовой дробилки в различных условиях.
Либервирт Х. привел результаты динамики фрагментации в экстремальных условиях, распределения частиц по размерам сопутствующих продуктов и влияния минеральной структуры различных горных пород на поведение при ударе. Kwon [2] был использован для характеристики поведения частиц измельченных продуктов двухвалковой дробилки и для прогнозирования распределения частиц по размерам измельченных продуктов. Soni S.K. [3] разработала модель, описывающую процесс дробления частиц в двухвалковой дробилке с гладкой поверхностью, для изучения распределения частиц продукта по размерам. Cleary Pw [4] смоделировал модель дробления с использованием метода дискретных элементов и изучил существующую щековую дробилку на основе оценки мощности, гранулометрического состава, производительности и износа дробилки. Ли [5] исследовал возможность использования метода дискретных элементов для моделирования производительности машины для измельчения в конусной дробилке. Было исследовано использование метода замены частиц для представления уменьшения размера горных пород, наблюдаемого в камере дробилки.
В этой статье, анализируя механизм дробления двухзубчатой роликовой дробилки, на основе предыдущих исследований автор анализирует влияющие факторы и порядок дробления двухзубчатой роликовой дробилки. С помощью программного обеспечения Solidworks и метода дискретного моделирования EDEM частицы соединяются в одно целое для имитации процесса реального дробления. Наилучшая схема испытания на дробление получается при использовании метода ортогонального испытания. Это справочное пособие для изучения гранулометрического состава продуктов дробления в двухзубчатой роликовой дробилке.
Двухзубчатая роликовая дробилка и модель материала
2.1. Механизм дробления и модель
- Материалы, попадающие вполость разрыва, измельчаются и дробятся (1-1 на 2-2);
- Материалы перемещаются к средней точке между сломанными зубьями и измельчаются комбинированной действие выдавливания и сдвига (2-2-3);
- Материалы падают до тех пор, пока стержень не будет снова сломан
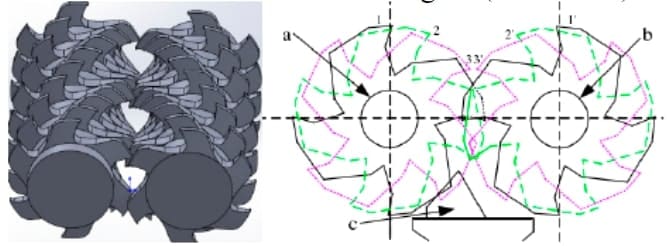
Рисунок 1. Модель дробилки на рисунке 2. Схема механизма дробилки
Можно видеть, что материалы в основном подвергаются удару на первом этапе, экструдированию и сдвигу на втором этапе, сдвигу и сгибанию на третьем этапе. В зависимости от механизма, расстояние между зубчатыми роликами, скорость вращения и угол наклона могут влиять на эффект дробления. Итак, влияние этих трех факторов на эффект дробления изучается далее.
Основной рабочей частью двухзубчатой роликовой дробилки являются два параллельно установленных дробильных ролика, с помощью которых материал измельчается путем уплотнения двух раздробленных роликов. Двухзубчатая роликовая дробилка в основном разделена на три этапа для измельчения материала, как показано на рисунке 1-2:
2.2. Калибровка материала и модель
Чтобы обеспечить точность моделирования, параметры моделирования необходимо откалибровать. Параметры модели горной породы включают макроскопические физические свойства и микромеханические свойства горных пород. Параметры макроскопических физических свойств относятся к коэффициенту Пуассона, плотности, модулю сдвига, коэффициенту столкновения горных пород, коэффициенту статического трения и коэффициенту трения качения; Параметры микромеханических свойств породы относятся к параметрам модели межзеренного взаимодействия в модели дискретных элементов, основанной на методе дискретных элементов, которые в основном включают единичную площадь связи межзеренного взаимодействия, нормальную жесткость, жесткость при сдвиге, нормальный предел прочности, предел прочности при сдвиге и действующий радиус связи [6]. Было проведено испытание на одноосное сжатие, и для калибровки использовался цилиндр диаметром 50 мм и высотой 100 мм, как показано на рисунке 3.
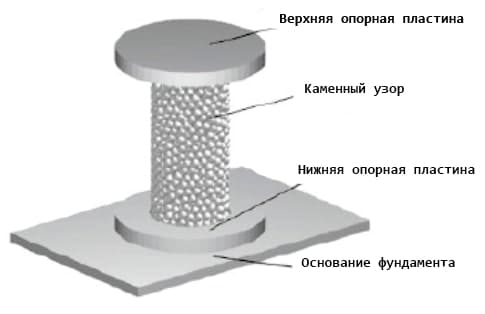
Рисунок 3. Модель одноосного сжатия
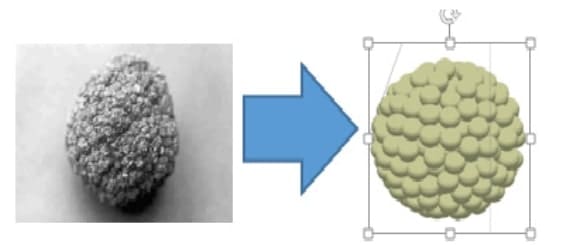
Рис. 4. Детализированная модель
После повторных испытаний форма разрушения дискретного элемента горной породы соответствует результатам испытания материала на сжатие, приведенным в таблице 1-3.
Таблица 1. Экспериментальные значения микромеханических свойств песчаника.
| Параметр | Нормальная жесткость на единицу площади (Н/м3) | Тангенциальная жесткость на единицу площади (Н/м3) | Нормальный предел прочности (Па) | Тангенциальный предел прочности (Па) |
|---|---|---|---|---|
| Сжимающий прочность | 4.0x109 | 4.0x108 | 2.1x107 | 2.1x106 |
Таблица 2. Макромеханические параметры материалов.
| Плотность материала | Коэффициент Пуассона | Плотность (кг/м3) | Модуль сдвига (Па) |
|---|---|---|---|
| Песчаник | 0.3 | 2600 | 2.7x1010 |
| Сталь | 0.3 | 7850 | 7.9x1010 |
Таблица 3. Параметры взаимодействия материалов.
| Коэффициент извлечения материала | Коэффициент статического трения | Коэффициент трения качения | |
|---|---|---|---|
| Песчаник - песчаниковый камень | 0.2 | 0.5 | 0.5 |
| Сталь - песчаник | 0.25 | 0.7 | 0.01 |
Сделаны следующие допущения, и модель показана на рисунке 4:
- Предполагая, что разрушенный материал имеет круглую геометрию и состоит из большого количества мелких частиц, соединенных связующими связями;
- Предполагая, что модель контакта частиц представляет собой мягкий шарик, может произойти деформация модуля, которая зависит от связующего соединения и радиуса контакта мелких частиц;
- Предполагая, что сила сцепления между мелкими частицами одинакова.
3. План тестового моделирования
3.1. Разработка плана тестирования
Из-за большого диапазона подачи и ограничения количества дискретных элементов необходимо упростить размер частиц в двухзубчатой роликовой дробилке. Распределение зерен по размерам показано в таблице 4 в соответствии с фактической ситуацией, чтобы гарантировать точность результатов.
Таблица 4. Упрощенный расчет гранулярности корма.
| Класс крупности частиц | Диапазон размеров (мм) | Соотношение (%) | Номер скалы |
|---|---|---|---|
| М1 | 900-1200 | 6.51 | 1 |
| М2 | 700-900 | 9.19 | 3 |
| М3 | 500-700 | 10.04 | 9 |
| М4 | 400-500 | 24.57 | 43 |
| М5 | 300-400 | 25.55 | 106 |
| М6 | 200-300 | 24.14 | 338 |
В соответствии с дробилкой m расстояние между роликами, частота вращения и угол наклона зубьев выбираются и обозначаются как A, B, C. Три уровня выбираются с помощью ортогональной таблицы L9(33) в таблице 5. Тестовым показателем является коэффициент разрушения соединения, дисперсия и среднее результирующее усилие. Коэффициент разрушения непосредственно влияет на гранулярность разгрузки; усилие зубчатого ролика непосредственно влияет на напряжение и деформацию ролика; отклонение результирующей силы отражает степень изменения результирующей силы в процессе дробления двухзубчатой роликовой дробилки. Чем меньше отклонение результирующей силы, тем лучше стабильность дробления.
Таблица 5. Таблица уровней факторов.
| Уровни | A: Расстояние между роликами (мм) | B: Скорость вращения (об/мин) | C: Угол наклона (°) |
|---|---|---|---|
| 1 | 1470 | 15 | 0 |
| 2 | 1490 | 18.75 | 12 |
| 3 | 1510 | 21 | 24 |
При моделировании EDEM скорость образования частиц составляла 5000 в/с, а начальная скорость - 9,8 м/с2. Общее число связей составило 152627. Время замены частиц составило 0,1 с, время склеивания - 0,1005 с, временной шаг - 1,5%, общее время моделирования - 40 с, размер ячейки - 150 мм.
3.2. Результаты моделирования и анализ
3.2.1 Результат моделирования
Поскольку дробилка с двойным зубом представляет собой два симметричных ролика, необходимо исследовать усилие на одном из роликов только при изучении результирующей величины. Согласно ортогональной таблице, было 9 групп, каждую группу моделировали 3 раза, изучали коэффициент разрушения соединения, дисперсию результирующей силы, записывали от начала до 0,4 с, интервал 0,2 с, всего 100 данных, и результат был показан в таблице 6.
Таблица 6. Результаты испытания на разрушение соединения при трех факторах и трех уровнях.
| N | Фактор | Коэффициент R (%) | R a(%) | F a(N)R a(%)𝜎2/f | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | M i1 | M i2 | M i3 | F i1 | F i2 | F i3 | 𝜎 2/Fi1 | 𝜎 2/Fi1 | 𝜎 2/Fi1 | ||
| 1 | 1 | 1 | 1 | 0.585 | 0.582 | 0.597 | 0.588 | 17.3 | 14.2 | 16.7 | 551 | 447 | 600 |
| 2 | 1 | 2 | 2 | 0.589 | 0.54 | 0.599 | 0.576 | 11.1 | 15.5 | 12.8 | 199 | 312 | 199 |
| 3 | 1 | 3 | 3 | 0.615 | 0.667 | 0.696 | 0.659 | 10.1 | 9.7 | 11.3 | 120 | 148 | 215 |
| 4 | 2 | 1 | 2 | 0.529 | 0.506 | 0.573 | 0.536 | 18.7 | 19.4 | 19.1 | 366 | 335 | 456 |
| 5 | 2 | 2 | 3 | 0.499 | 0.499 | 0.534 | 0.511 | 15.7 | 14.3 | 15.8 | 262 | 274 | 277 |
| 6 | 2 | 3 | 1 | 0.431 | 0.469 | 0.453 | 0.451 | 15.4 | 14.3 | 18.0 | 660 | 652 | 546 |
| 7 | 3 | 1 | 3 | 0.637 | 0.604 | 0.608 | 0.616 | 21.9 | 12.5 | 15.8 | 677 | 175 | 209 |
| 8 | 3 | 2 | 1 | 0.602 | 0.606 | 0.610 | 0.606 | 21.2 | 18.1 | 17.9 | 745 | 365 | 478 |
| 9 | 3 | 3 | 2 | 0.422 | 0.496 | 0.475 | 0.464 | 19.2 | 15.6 | 15.2 | 630 | 294 | 269 |
| M j1 | 5.47 | 5.22 | 4.94 |
Индекс: Коэффициент разрушения соединения Основной фактор: A,B,C Высший уровень:A 1,C 3, B 1 Оптимальное сочетание: A 1, C 3, B 1 |
|||||||||
| M j2 | 4.49 | 5.08 | 4.73 | ||||||||||
| M j3 | 5.06 | 4.72 | 5.36 | ||||||||||
| M j1 | 1.82 | 1.74 | 1.65 | ||||||||||
| M j1 | 1.50 | 1.69 | 1.58 | ||||||||||
| M j1 | 1.69 | 1.57 | 1.79 | ||||||||||
| R mj | 0.32 | 0.17 | 0.21 | ||||||||||
| 𝜎 2/Fj1 | 2791 | 3816 | 5044 |
Индекс : Отклонение результирующей силы Основной фактор: A,B,C Высший уровень:C 3,A 1, B 2 Оптимальное сочетание: C 3, A 1, B 2 |
|||||||||
| 𝜎 2/Fj2 | 3828 | 3111 | 3060 | ||||||||||
| 𝜎 2/Fj3 | 3842 | 3534 | 2357 | ||||||||||
| 𝜎 2/FFj1 | 930.3 | 1272.0 | 1681.3 | ||||||||||
| 𝜎 2/Fj2 | 1276.0 | 1037.0 | 1020.0 | ||||||||||
| 𝜎 2/Fj3 | 1280.7 | 1178.0 | 785.7 | ||||||||||
| R𝜎 2/Fj | 350.4 | 235 | 895.6 | ||||||||||
| 𝜎 2/Fj1 | 2791 | 3816 | 5044 |
Индекс : Средняя результирующая сила Основной фактор: A,B,C Высший уровень:A 1,B 3, C 3 Оптимальное сочетание: A 1, B 3, C 3 |
|||||||||
| Fj2 | 118.7 | 155.9 | 153.1 | ||||||||||
| Fj3 | |||||||||||||
| F j1 | 151.0 | 142.4 | 149.9 | ||||||||||
| F j2 | 157.4 | 128.8 | 127.1 | ||||||||||
| F j3 | 39.6 | 52.0 | 51.0 | ||||||||||
| RFj1 | 50.3 | 47.5 | 49.0 | ||||||||||
Примечание: отклонение результирующей силы умножается на 10 12N, а средняя результирующая сила умножается на 104N.
N - представляет количество тестовых групп.
Коэффициент представляет собой коэффициент разрушения соединения.
R a - представляет собой среднее значение коэффициента разрушения соединения
F a - представляет собой среднее значение результирующей силы
𝜎2/F - представляет собой отклонение результирующей силы.
Исходя из данных, приведенных в таблице 6, выполните моделирование: кривая коэффициента разрушения всего процесса отмечена черной линией, значок звезды; кривая среднего усилия отмечена красной линией, значок треугольника; отклонение отмечено синей линией, значок ромба. В то же время необходимо построить кривую влияния трех индексов, чтобы более наглядно показать порядок трех факторов и уровней. На рисунке 6 показаны расстояние между роликами, скорость вращения роликов, эффект угла наклона спирали сверху вниз соответственно. Диапазон изменения больше, влияние на коэффициент разрушения такое же, среднее значение и дисперсию кривой силового воздействия можно получить на рисунке 7-8.
3.2.2 Анализ результатов
Согласно рисунку 5-8, расстояние является основным фактором, влияющим на эффект дробления и среднее результирующее усилие зубчатого ролика. Для кривой эффекта кривая сначала уменьшается, а затем увеличивается с увеличением расстояния. Угол наклона и скорость вращения вторичных факторов могут незначительно влиять на коэффициент разрушения, показанный на рисунке 6; что касается кривой среднего результирующего усилия, то удивительно, что кривая не уменьшается, а увеличивается с увеличением расстояния между роликами на рисунке 7.; для кривой влияния дисперсии результирующей силы эффект увеличения расстояния между валками такой же, как и для кривой средней результирующей силы. Важным результатом кривой является то, что дисперсия результирующей силы уменьшается с увеличением угла наклона на рисунке 8.
Угол наклона зубьев является наиболее важным фактором в процессе дробления, а также оказывает важное влияние на эффект дробления. Чем больше угол наклона, тем меньше отклонение результирующей силы, что указывает на то, что процесс дробления более стабилен.
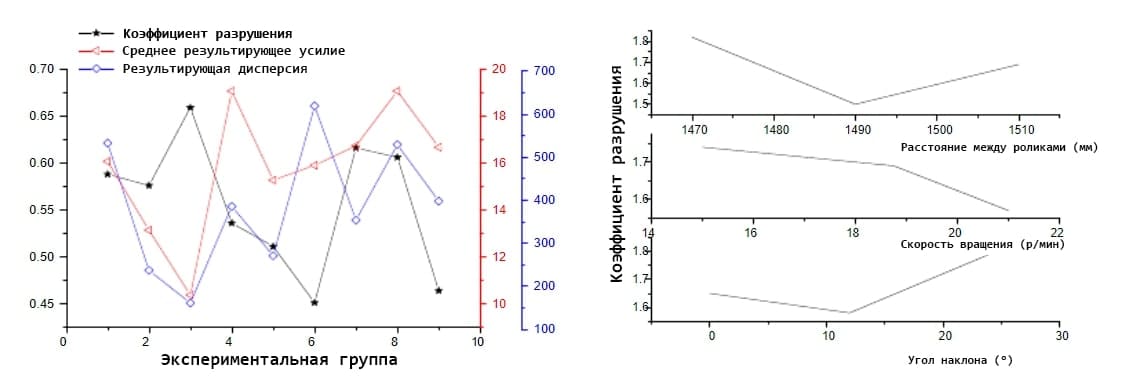
Рисунок 5. Диаграмма данных процесса тестирования Рисунок 6. Кривая влияния коэффициента разрушения
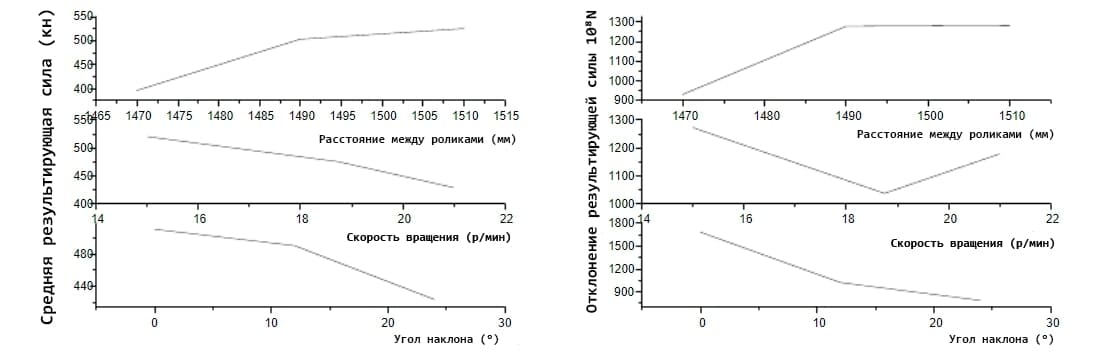
Рисунок 7. Средняя кривая результирующего силового эффекта Рисунок 8. Отклонение кривой результирующего силового эффекта
4. Заключение
Основываясь на методе дискретных элементов и ортогональном эксперименте, в данной статье делаются следующие выводы:
- Основными и второстепенными факторами, влияющими на коэффициент разрушения соединения, являются расстояние между роликами, угол наклона, скорость вращения; Основными и второстепенными факторами, влияющими на изменение результирующего усилия, являются угол наклона, расстояние между роликами, скорость вращения; Основными и второстепенными факторами, влияющими на среднее результирующее усилие, являются ролик расстояние, скорость вращения и угол наклона.
- Согласно анализу эффекта дробления и ситуации с усилием, основным фактором является эффект дробления, сначала рассчитайте расстояние между роликами; основным фактором является стабильность процесса дробления, сначала рассчитайте угол наклона.
- Конечно, в статье есть много недостатков. Различные компоненты материалов будут влиять на процесс дробления в двухзубчатой роликовой дробилке. Однако в этой статье выдвигается новая идея для изучения размера частиц и эффекта дробления, которая обеспечивает основу для проектирования двухзубчатой роликовой дробилки.
Подтверждение
Эта работа была поддержана ключевыми научными и технологическими исследовательскими проектами на основе угля в Шаньси (грант № MJ2014-02).
Ссылки
-
Lieberwirth Hand Hillmann P 2017 Динамика в двухвалковых дробилках Minerals Engineering 103-104: стр. 60-66.
-
Kwon J 2012 Моделирование дробления угля в двухвалковой дробилке с учетом явлений повторной агломерации Порошковая технология 232 (2012) 113-123
-
Сони С. К. и Шукла С. С. Моделирование разрушения частиц в двухвалковой дробилке с гладкой поверхностью. Инт. Дж. Майнер. Процесс. 90 (2009) 97–100
-
Клири П.У. и Синнотт М.Д. 2015 Моделирование потоков частиц и разрушения в дробилках с использованием DEM: Часть 1 – Компрессионные дробилки Minerals Engineering 74: стр. 178-197.
-
Huiqi L и McDowell Glenn 2014 Дискретно-элементное моделирование порошковой технологии конусной дробилки горных пород 2014. 263: стр. 151-158.
-
Уильямс-младший и Хокинг Г. 1985 Теоретические основы метода дискретных элементов Материалы конференции NUMETA 85, 1985, 897-906.