В библиотеку

УДК 517.587+519.651.3+534.4

ПРОГНОЗ ВРЕМЕННЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ С ИСПОЛЬЗОВАНИЕМ ОБОБЩЁННОГО СПЕКТРАЛЬНО-АНАЛИТИЧЕСКОГО МЕТОДА

А.К. Бритенков, Ф.Ф. Дедус

Нижегородский госуниверситет им. Н.И. Лобачевского

Институт математических проблем биологии РАН, Пущино

Источник: Вестник нижегородского университета им. Н.И. Лобачевского, 2012, №5(2) [ссылка]

А.К. Бритенков, Ф.Ф. Дедус ПРОГНОЗ ВРЕМЕННЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ С ИСПОЛЬЗОВАНИЕМ ОБОБЩЁННОГО СПЕКТРАЛЬНО-АНАЛИТИЧЕСКОГО МЕТОДА На основе обзора регрессионных моделей рассмотрено применение обобщённого спектральноаналитического метода для прогноза временных рядов, эффективного в задачах описания и распознавания сигналов. Предлагается использование ортогональных базисов на основе классических полиномов непрерывного аргумента в задачах прогноза как частного случая экстраполяции. Проанализировано применение дополнительных данных для улучшения достоверности прогноза

Ключевые слова: прогноз временных рядов, регрессия, обобщённый спектрально-аналитический метод, классические ортогональные полиномы, метод наименьших квадратов, экстраполяция, системный анализ.

Краткий обзор методов прогнозирования

Методы прогнозирования временных рядов [1] условно можно разделить на несколько направлений [2]. К первому направлению относятся аппроксимативные методы прогноза [3], например динамический анализ, модели экспоненциального сглаживания (ARIMA), метод декомпозиции временных рядов (тренд, сезонность, случайность, выделение циклической компоненты), выделение скрытых периодичностей (спектральный анализ, анализ периодограммы) [4]. Другое направление, применяя комплексный подход к решению задач прогноза, предполагает использование нейросетевых методов, метода парадигм, регрессионного анализа (AR(p), ARMA(p, q) и т.д.) и статистических оценок [3]. В описательном анализе [5] используются выборочные характеристики временных рядов: среднее, дисперсия, автокорреляционная функция, частная автокорреляционная функция, распределения выборочных характеристик, стационарность временного ряда [6]. Прогнозирование на основе пропорциональных зависимостей и комбинированные методы [7] могут включать в себя также экспертные оценки и применение методов множественной регрессии [2], анализ распределенных лагов (сетевых задержек, когда на прогноз оказывают влияние более ранние события, чем происходящие непосредственно накануне прогноза) и оценки адекватности модели прогноза. В последнем случае результаты, полученные с помощью модели, сравниваются с фактическими значениями через какой-то промежуток времени, когда те появляются [5]. Недостаток такого подхода состоит в том, что проверка «беспристрастности» модели может занять много времени, так как по-настоящему проверить модель можно только на продолжительном временном отрезке [8].

Параметры прогноза временных рядов

Регрессионные модели прогноза используют описание независимой переменной y с помощью зависимой переменной x [2]. Прогноз в дальнейшем – результат подстановки новых значений x в найденное функциональное уравнение y = f(x). В качестве такой функции часто используются аппроксимирующие функции. Аппроксимация с помощью классических ортогональных функций [9], где расчёт коэффициентов предполагается по методу наименьших квадратов (МНК), наиболее удовлетворяет перечисленным критериям [10][11]. В регрессионных моделях, где функциональная зависимость также ищется в виде функции, наилучшим образом приближающей искомую кривую с помощью МНК, вводится понятие функции невязки

$ \sigma (b)= \frac{1}{2}\sum_{k=1}^{M}{(Y_{k}-\hat{Y_{k}})}^2 $

где M – объём выборки. Поиск минимума невязки отклонений реально наблюдаемых Y от их оценок Ŷ (имеются в виду оценки с помощью кривой, претендующей на то, чтобы представлять искомую регрессионную зависимость) основан на том, что согласно МНК сумма в выражении (1) принимает минимальное значение именно тогда, когда Y = y(x1,x2,...xN). Временная последовательность s(t), описываемая ортогональным рядом вида

$s(t)=\sum_{i=0}^{N}A_i\phi _i(t)$

где φi – ортогональный базис (полученный модификацией классических ортогональных полиномов, которые являются частным случаем решения гипергеометрического уравнения [12, 13]), как было отмечено выше, так же подразумевает невязку вида (1) для вычисления Ai:

$ A_i = \left \| \phi _i \right \|^{-2}\int_{0}^{T}\phi _i(t)f(t)\rho (t)dt $

Таким образом, под параметрами прогноза подразумеваются длина выборки М, глубина прогноза (количество шагов), порядок модели (для АR – p), ошибка прогноза [14].

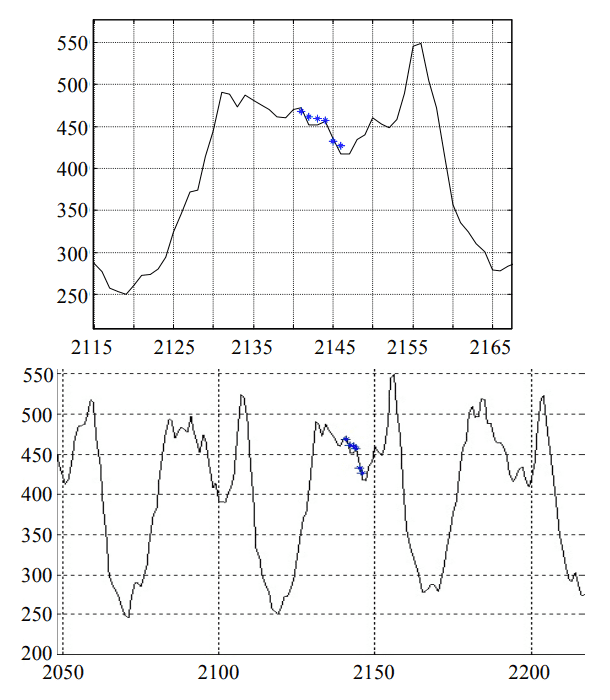
Прогноз энергопотребления авторегрессионной моделью (AR(p), p = 480), длина выборки N = 2100 точек (48 отсчетов в сутки), прогноз составлен на 6 шагов вперед (3 часа)

Прогноз временных рядов ортогональными базисами непрерывного аргумента

Применение обобщенного спектрально-аналитического метода (ОСАМ) для прогнозирования потоков данных, определение задачи прогноза как частого случая экстраполяции и фильтрации помех исходит из того, что, как показано выше, МНК, применяемый в регрессионных методах прогноза, идентичен МНК при вычислении коэффициентов ряда Фурье [11][15]. Предполагается, что разработка методов с использованием свойств ортогональных базисов на основе классических полиномов непрерывного аргумента (в задачах, где тригонометрические ряды Фурье менее эффективны, например [16]) позволяет расширить возможности математического аппарата ОСАМ, разработанного во второй половине XX века [17].

Проводя аналогию регрессии с физическими моделями, рассмотрим систему, содержащую N отражательных поверхностей для акустических волн [18]. Математически такая система напоминает регрессионную модель. Действительно, в такой системе исходный звуковой сигнал S(t) преобразуется в S* (t) так, что в общем случае S* (t) можно представить суммой дискретных задержанных импульсов и ослабленного после прохождения через среду исходного сигнала

$ S*(T)=\alpha _0S(t)+\sum_{i=1}^{N}\alpha _1S(t-\tau _i)=\sum_{i=0}^{N}\alpha _1S(t-\tau _i) $

где αi – коэффициенты отражения; τi – задержка во времени одного отражения, N – число пришедших в приемник отражений (первичных, вторичных и т.д.). Для сигнала, достигшего приемника без отражений, τ0 = 0. Решение с помощью обобщенного спектрально-аналитического метода обратной задачи о распространении звука в условиях дискретных отражений [19] показывает возможность использования подобной технологии как компонента регрессионного моделирования.

Определение параметров прогноза квазипериодических сигналов с аддитивным шумом

В каждом реальном сигнале присутствует шум. Особенно это относится к задачам обработки временных рядов, когда шум присутствует естественным образом в самой системе или механизме измерений. В финансовых приложениях, статистических параметрах социальных задач данные зашумлены особенно сильно. Например, данные о совершении сделок или котировки ценных бумаг и другие показатели могут регистрироваться с запозданием, причем в различных случаях – с разным. Пропуск значений или неполная информация также рассматривается как шум. Использование в таких случаях на коротком отрезке среднего значения вместо отсутствующего отсчета приводит к зашумлению данных. Таким образом, для успешного прогнозирования необходима эффективная обработка входных данных, в частности минимизация случайных флуктуаций и шума.

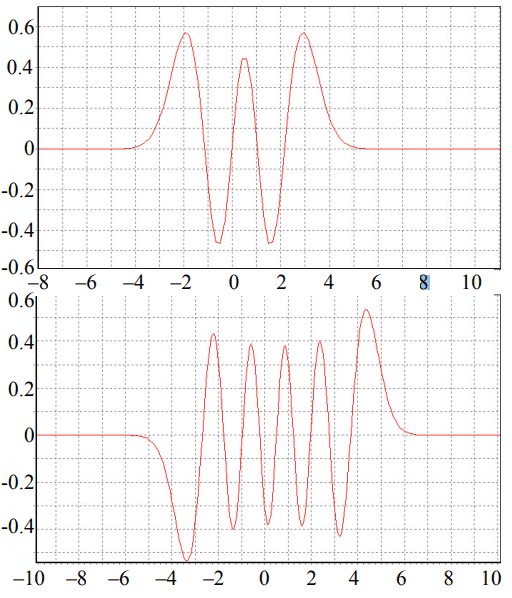
Фильтрации шума посвящено большое количество работ. Условно можно разделить методы шумоподавления на спектральные [18][20], и статистические [21], не пренебрегая, разумеется, и их комбинацией [20][22]. В ряде работ спектральные методы используют вейвлетанализ, как, например, в работах [20][23]. В этих случаях также возможно применение ортогональных базисов на основе классических полиномов непрерывного аргумента как базисных вейвлетов. Примером такого вейвлета является функция Эрмита (рис. 2):

$ H-n(t)=1/(2Г(-n))\sum_{k=0}^{\infty}{(-1)}^kГ({\frac{k-n}{2}})\frac{t^k}{k!} $

где Г – гамма-функция, n – порядок функции Эрмита.

Функция Эрмита (Hn(t), n = 4, n = 9)

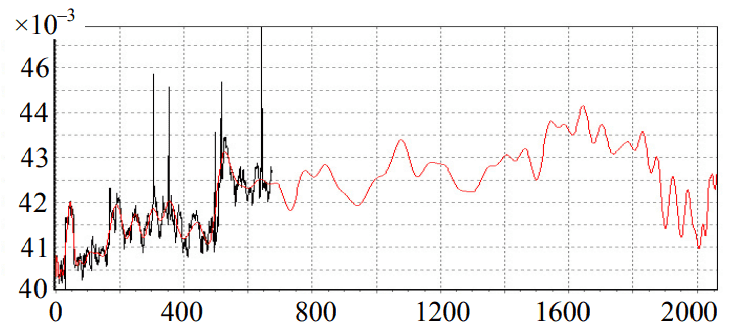
Идея использования классических ортогональных полиномов для прогноза (экстраполяции) основана на том, что фактически такая экстраполяция является частным случаем выделения сигнала на фоне помех (рис. 3).

Однако простое продление аппроксимирующей кривой за пределы доступных данных не всегда приводит к успешному предсказанию. С другой стороны, использование ортогональных базисов на основе полиномов непрерывного аргумента из числа классических в задаче со статистическими методами также является логичным ввиду математического аппарата ОСАМ:

Прогноз-экстраполяция потребления электроэнергии предприятия (кВт/ч) функциями Лежандра (Pn(t), n = 100, число шагов прогноза более 1000, число «обучающих точек» р = 675)

получение статистических соотношений на основе коэффициентов разложения (2) оптимизирует вычислительные процедуры [10, 17].

Алгоритмы оптимизации прогноза и дополнительные данные

Прогнозирование одномерных сигналов и временных данных можно существенно улучшить, используя дополнительные данные, например корреляцию прогнозируемых сигналов с другими параметрами, испытывающими колебания на той же временной оси. В случае с энергопотреблением предприятия такими данными могут быть план производства, температура окружающей среды и собственно время (время суток, день недели, время года). В этих графиках спектральный анализ позволяет выделить характерные периоды, что дает дополнительные данные для уточнения прогноза. Синергетический подход показывает, что колебания прогнозируемой величины и дополнительных данных представляют с разных сторон исследуемую единую систему [24], поэтому корреляция между ними очевидна (рис. 4, 5).

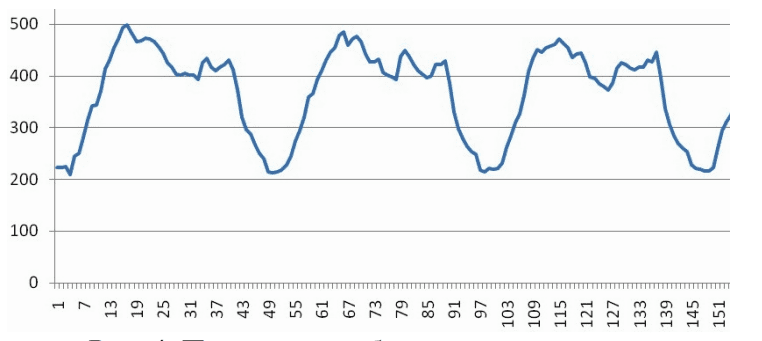
Пример потребления электроэнергии предприятия (кВт/ч) в течение 3 дней
Циклическое представление времени на оси отсчетов данных электропотребления предприятия в течение 3 дней

Обсуждение результатов

Актуальность классических ортогональных функций и обобщенных рядов Фурье подтверждается использованием их в описании случайных процессов [20], решении дифференциальных уравнений [25], моделировании оптических негармонических импульсов [26], эмпирических базисах в гидрофизике [16], развитии вейвлетанализа [27] и обобщенного спектрально-аналитического метода [5][10][14][15].

Исходя из природы используемых данных (котировок ценных бумаг, показателей электропотребления предприятия), анализ дополнительных условий на входные данные, а также конкретизация «физики» колебаний показателей временных последовательностей для составления прогноза является важнейшим условием повышения точности прогноза. Математически это определение таких критериев решения, как ошибка аппроксимации; точность предсказания и выбор параметров прогнозирования; оценка статистических характеристик исходных данных, фильтрация шума, корреляция с параллельными потоками данных. На следующем этапе реализуется оптимизация способа аппроксимации дискретных данных разложением по классическим ортогональным базисам. Однако построение прогноза временного ряда, использующее экстраполяцию аппроксимирующей функцией, требует комбинации с другими методами (например, регрессионным анализом), поскольку в соответствии со скалярным произведением (3) нужны ненулевые данные f(t) (или модели) для вычисления коэффициентов разложения на участке прогноза.

Важность системного подхода продиктована требованием целостного решения задач с элементами выбора, принятия решений и поискаs наилучшей стратегии [7]. Математические методы описания и анализа сложных экономических, социальных, экологических систем показали, что кроме объективных законов в функционировании смешанных систем существенную роль играют субъективные представления [8]. Поскольку в таком случае не представляется возможным формализовать (или количественно описать) реальную систему и, таким образом, построить адекватную математическую модель, только системный подход и интеграция различных методов (в т.ч. эвристических приемов) позволяет по-настоящему эффективно решать подобные задачи [28].

Обсуждение результатов