УДК 681.518:551.50:551.501
АЛГОРИТМ ПОИСКА МОМЕНТА СМЕНЫ ТРЕНДА ВО ВРЕМЕННЫХ РЯДАХ МЕТЕОРОЛОГИЧЕСКИХ ВЕЛИЧИН
Кузнецов А.Д., Саенко А.Г., Сероухова О.С., Симакина Т.Е.
Российский государственный гидрометеорологический университет, г. Санкт-Петербург
Источник: Вестник ТвГУ. Серия: Прикладная математика. 2019. № 3. С. 74–89. [ссылка]
Кузнецов А.Д., Саенко А.Г., Сероухова О.С., Симакина Т.Е. АЛГОРИТМ ПОИСКА МОМЕНТА СМЕНЫ ТРЕНДА ВО ВРЕМЕННЫХ РЯДАХ МЕТЕОРОЛОГИЧЕСКИХ ВЕЛИЧИН Предложен алгоритм нахождения точки бифуркации во временном ряду. Проведено моделирование влияния погрешности измерений на устойчивость нахождения точки бифуркации.
Ключевые слова: временные ряды метеорологических величин, анализ временных рядов, временной тренд, точка бифуркации.
Введение
Анализ временных рядов метеорологических элементов широко используется как в климатических исследованиях, так и для целей прогноза, в том числе с наименьшей заблаговременностью – наукастинга [1][2]. Существует большое количество методов обработки стационарных временных рядов [3][4][5]. Однако, климатические факторы и метеорологические элементы характеризуются значительной изменчивостью, имеющей сложную стохастически-детерминированную физическую природу. Соотношение случайной и закономерной составляющих общей изменчивости временного ряда оценивается путем выявления и удаления статистически значимых монотонных и циклических трендов [6]. В результате этого существенно уменьшается общая дисперсия исследуемого показателя, что повышает надежность и точность его вероятностной и прогнозной оценок.
Для сверхкраткосрочного и текущего прогнозов временных рядов метеорологических или экологических элементов пользуются экстраполяцией текущих значений на будущее [2]. Однако методы экстраполяции допустимы в рамках одного процесса, но не дают положительного результата в период их смены. Поэтому большинство задач анализа временных рядов упираются в вопрос: происходит ли смена господствующего процесса, порождающего данный временной ряд, на протяжении исследуемого периода. В качестве иллюстрации сказанного на Рис. 1 представлен временной ряд концентрации тропосферного озона, измеренный в Санкт-Петербурге зимой 2018-2019 гг. [7]. Визуальный анализ не позволяет дать однозначный ответ, содержит ли данный ряд возрастающий линейный тренд, или он состоит из трех интервалов с разной тенденцией развития, подчиняющейся разным процессам. Рис. 1а – общий ряд с линейным трендом, надежность которого 0,29 (коэффициент детерминации); Рис. 1б – ряд разбит на три интервала, надежность тренда на каждом – 0,47, 0,85 и 0,92 соответственно.
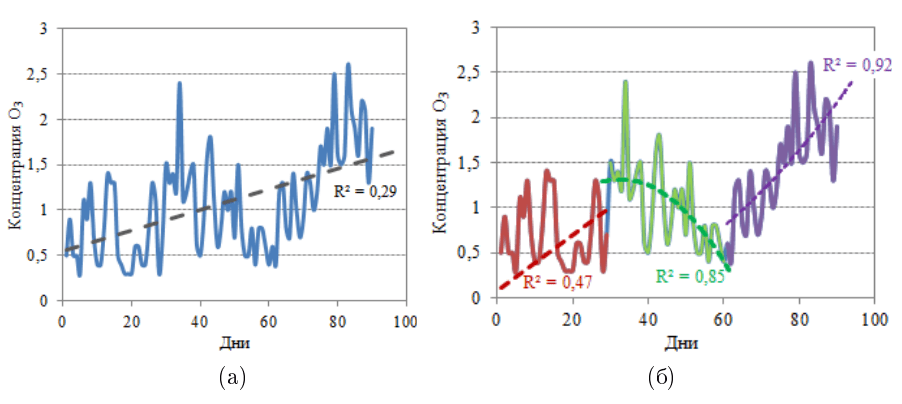
Таким образом, одним из этапов исследования различных временных рядов является определение наличия моментов времени смены процессов, которым подчинялось поведение временного ряда. Момент времени в исследуемом ряду, соответствующий резкому изменению характера протекающего процесса, т. е. смене тренда, можно считать «точкой бифуркации». В интервалах между бифуркациями поведение системы предсказуемо, оно определяется и случайными, и закономерными факторами. Для нахождения положения точки бифуркации возможно использование тренда в качестве математической модели отрезков временного ряда [8]. Однако такой подход наталкивается на трудности, в частности, связанные с тем, что не существует «автоматического» способа обнаружения тренда во временном ряду. Более того, нет даже единого формального определения тренда.
Целью данной работы является построение методики поиска точек бифуркации на основе анализа временного ряда, отражающего поведение системы.
1. Алгоритм поиска точек бифуркации
В основе алгоритма определения положения точек бифуркации лежит сравнение между собой разных отрезков временного ряда. Задача решается заменой отрезков временного ряда их математической моделью. В качестве моделей могут быть использованы полиномы разных степеней, начиная от полинома нулевой степени. При таком подходе каждая степень полинома определяет геометрическую форму отрезков временного ряда между точками бифуркации. Для полинома нулевой степени это число, которое будет определять на графике временного ряда положение прямой линии, параллельной горизонтальной оси времени (так называемый метод 𝐾-средних). Для полинома первой степени – это отрезки прямых, для полинома второй степени – это параболы и т. д.
Таким образом, определение положения точек бифуркации включает следующие этапы:
- формирование на основе прямого перебора отрезков разной длины;
- построение для них математических моделей;
- оценка успешности каждого такого разбиения с помощью одного или нескольких количественных критериев, рассчитываемых с использованием соответствующих метрик [9].
Рассмотрим алгоритм нахождения положения точки бифуркации с использованием полинома нулевой степени. В этом случае значения всего временного ряда аппроксимируются двумя горизонтальными линиями, граница между которыми определяет положение точки бифуркации.
Пусть имеется временной ряд из 𝑁 значений 𝑦(𝑥): [𝑥𝑖 , 𝑦𝑖 ], 𝑖 = 1, 2, . . . ,𝑁. Разделим этот ряд на два отрезка: [1, 𝑛1] и [𝑛1+1, 𝑁] (при таком разделении значение 𝑛1 может меняться от 2 до 𝑁 − 1, а общее число таких разделений будет равно 𝑁 − 3). Вычислим при каждом таком разбиении для каждого отрезка два соответствующих им параметра по формулам:
$a_0=\frac{1}{N_1}\sum_{i=1}^{n_1}y_i$
$a_1=\frac{1}{N_2}\sum_{i=n_1+1}^{N}y_i$
где 𝑁1 = 𝑛1 и 𝑁2 = 𝑁 – 𝑛1.
Оценим «близость» полученных параметров значениям временного ряда, использую метрику SS – аналог минимизации значения среднеквадратического отклонения тренда от значений временного ряда (набор метрик, которые могут быть использованы для этой же цели, рассмотрены авторами в работах [10, 11]). Рассмотрев все 𝑁 – 3 значений параметра SS, найдем то значение 𝑛1, при котором будет выполняться условие:
$SS=\sum_{i=1}^{n_1}{(a_0-y_i)}^2+\sum_{i=n_1+1}^{N}{(a_1-y_i)}^2=min$
Найденное таким образом значение 𝑛1 и будет определять положение точки бифуркации временного ряда при использовании полинома нулевой степени и метрики (3).
Рассмотрим алгоритм нахождения положения точки бифуркации с использованием полинома первой степени.
Проведя разделение временного ряда на два отрезка так, как это было описано выше, вычислим для каждого отрезка две пары коэффициентов линейного временного тренда по формулам:
$ a_{11} = \frac{ n_1\sum_{i=1}^{n_1}y_ix_i - \sum_{i=1}^{n_1}y_i\sum_{i=1}^{n_1}x_i }{ n_1\sum_{i=1}^{n_1}x_i^2-{(\sum_{i=1}^{n_1}x_i)}^2 },\,a_{01}=\frac{1}{n_1}\sum_{i=1}^{n_1}y_i-a_{11}\sum_{i=1}^{n_1}x_i $
$a_{11} = \frac{ (N-n_1)\sum_{i=n_1+1}^{N}y_ix_i - \sum_{i=n_1+1}^{N}y_i\sum_{i=n_1+1}^{N}x_i }{ (N-n_1)\sum_{i=n_1+1}^{N}x_i^2-{(\sum_{i=n_1+1}^{N}x_i)}^2 }$
$a_{01}=\frac{1}{N-n_1}\sum_{i=n_1+1}^{N}y_i-a_{12}\sum_{i=n_1+1}^{N}x_i$
Тогда положение точки бифуркации определяется таким номером 𝑛1, для которого выполняется следующее условие (считая, что ряд эквидистантный и можно провести следующую замену: 𝑥𝑖 = 𝑖):
$SS=\sum_{i=1}^{n_1}{(a_{01}+a_{11}i-y_i)}^2+\sum_{i=n_1+1}^{N}{(a_{02}+a_{12}i-y_i)}^2=min$
Для оценки «эффективности» произведенного разделения ряда на два отрезка с использованием полиномов нулевой и первой степеней можно воспользоваться сравнением дисперсии всего ряда 𝜎ряда и суммарной дисперсии 𝜎ступ двух его отрезков, вычисленных по формуле:
$ \sigma_{ступ}=\sqrt{\frac{\sigma_1^2 \bullet N_1+\sigma_2^2 \bullet N_2}{N_1+N_2-1}} $
где 𝑁1 и 𝑁2 – длина первого и второго отрезка ряда, разделенные точкой бифуркации, 𝜎1 и 𝜎2 – среднеквадратическое отклонение значений двух отрезков временного ряда от двух отрезков линейного тренда.
Для оценки значимости проведенного разделения сравним значение критерия Фишера:
$ F=\frac{\sigma_{ряда}^2}{\sigma_{ступ}^2}} $
с критическим значением 𝐹кр.
Если выполняется неравенство 𝐹 >𝐹кр, то будем считать, что проведенное разделение статистически значимо с заданной при определении 𝐹кр доверительной вероятностью 𝛼.
Аналогичным образом, для задания формы временных трендов могут быть рассчитаны коэффициенты полиномов и более высоких (чем первый) порядков.
Анализ влияния порядка полинома на определение положения точки бифуркации
Анализировалось влияние порядка трендов, используемых для аппроксимации отрезков временного ряда, на положение точки бифуркации. При проведении численных экспериментов в качестве исходного был взят ряд средней глобальной температуры Земли на уровне 2 м с дискретностью 1 год [8]. Степень полинома варьировалась в диапазоне от 0 до 3.
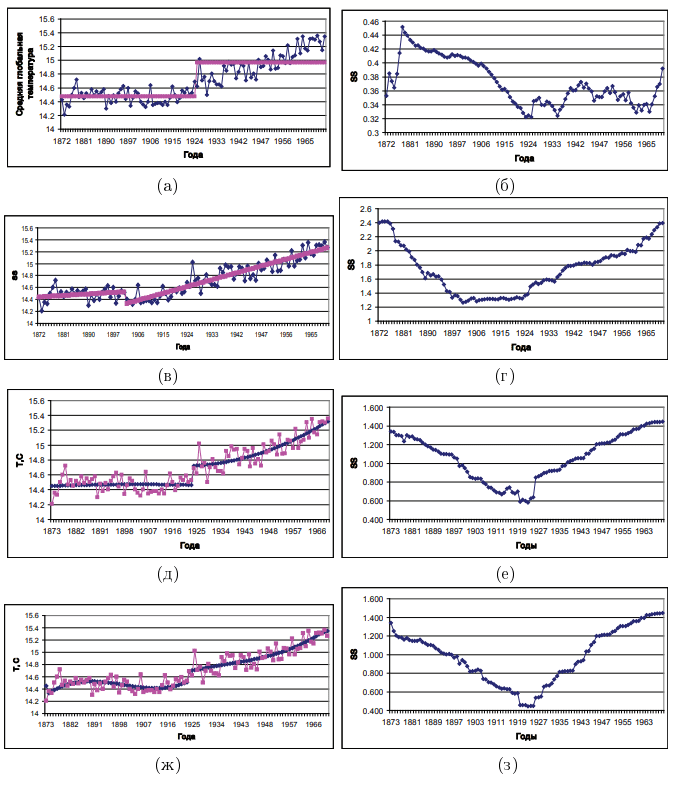
Типичные результаты, полученные при изменении степени полинома, иллюстрирует Рис. 2. Здесь Рис. 2 (а), (в), (д) и (ж) – это положения аппроксимирующих временной ряд трендов, описываемых, соответственно, полиномами нулевого, первого, второго и третьего порядков. При этом положение точки бифуркации по мере увеличения степени полинома, соответственно, меняется следующим образом: 𝑛1 = 57 (1925 год), 𝑛1 = 33 (1901 год), 𝑛1 = 55 (1923 год) и 𝑛1 = 55 (1923 год).
Рис. 2 (б), (г), (е) и (з) показывают, как по мере увеличения степени полинома меняется временная изменчивость используемой для определения положения точки бифуркации метрики. Повышение степени полинома приводит к более четкому экстремуму кривой значений метрики SS. Так, на Рис. 2б кривая SS имеет несколько локальных минимумов, на Рис. 2г четкий экстремум отсутствует, «минимальное плато» занимает промежуток длительностью в 25 лет, на Рис. 2е присутствуют кроме абсолютного минимума еще «квазиминимум» несколькими годами ранее, и только на Рис. 2з, соответствующим полиному 3-ей степени, наблюдается четкий глобальный минимум, однозначно указывающий на год точки бифуркации. Данный пример наглядно иллюстрирует, насколько, казалось бы, объективный метод определения положения точки бифуркации может быть субъективен, несмотря на использование строгих количественных оценок.
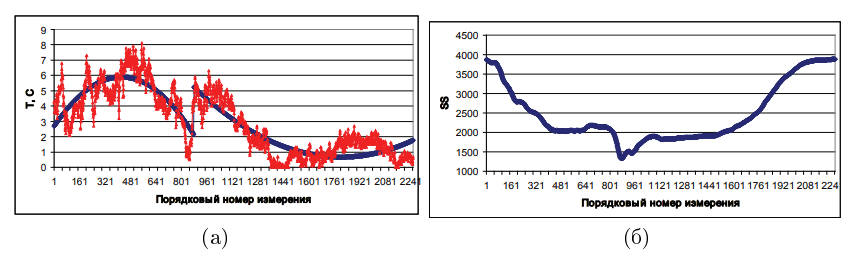
Преимущества использования полиномов порядка выше 1 иллюстрирует Рис. 3. Здесь нахождение положения точки бифуркации производится для весьма протяженного временного ряда, содержащего 2259 значений температуры воздуха, измеренных автоматической метеорологической станцией с дискретностью 15 мин. Временной ряд имеет весьма сложную структуру. Но это не помешало двум полиномам второй степени весьма успешно по предложенному алгоритму разделить его на две части, найдя положение точки бифуркации как 𝑛1 = 879.
Заключение
Изучение таких нелинейных явлений, как бифуркации, имеет большое прикладное значение, так как они соответствуют кризисным событиям в моделируемых системах. Предложенный в данной работе подход позволяет автоматизировать поиск положения точки бифуркации во временных рядах. В тоже время, приведенное исследование показывает те сложности, которые возникают при интерпретации казалось бы объективных результатов, связанных с определением положения точки бифуркации.
Рассмотренные алгоритмы носят универсальный характер и могут быть применены к исследованию временных рядов самого разнообразного характера.
Доказано, что повышение степени полинома способствует локализации экстремума в значениях метрики.
Список использованных источников
- Восканян К.Л., Дивинский Л.И., Кузнецов А.Д., Сероухова О.С., Симакина Т.Е. Применение сплайн-экстраполяции для текущего прогнозированияприземной температуры воздуха // Труды Военно-космической академии им.А.Ф. Можайского. 2015. № 647. С. 88–92.
- Кузнецов А.Д. Текущее прогнозирование на основе цифровой обработки изображений. СПб.: Изд-во РГГМИ, 1997. 167 с.АЛГОРИТМ ПОИСКА МОМЕНТА СМЕНЫ ТРЕНДА ВО ВРЕМЕННЫХ... 85
- Восканян К.Л., Кузнецов А.Д., Сероухова О.С. Автоматические метеорологические станции. Часть 2. Цифровая обработка данных автоматических метеорологических станций. Учебное пособие. Санкт-Петербург: РГГМУ, 2015.80 с.
- Алдошкина Е.С., Кузнецов А.Д., Пугачев А.А., Сероухова О.С., СимакинаТ.Е., Чукин В.В. Опыт использования аппарата нейронных сетей для анализа и прогноза временного ряда температуры воздуха // Ученые запискиРоссийского государственного гидрометеорологического университета. 2009.№ 11. С. 91–100.
- Малинин В.Н. Статистические методы анализа гидрометеорологической информации. СПб.: РГГМУ, 2008. 407 с.
- Восканян К.Л., Кузнецов А.Д., Сероухова О.С., Симакина Т.Е. К вопросу овыделении аддитивных составляющих временного ряда приземной температуры воздуха // Ученые записки Российского государственного гидрометеорологического университета. 2013. № 32. С. 55–65.
- Экологический портал Санкт-Петербурга [Электронный ресурс]. URL:http://www.infoeco.ru/index.php?id=53.
- Логинов В.Ф., Микушкина В.С. Изменение климата. Тренды, циклы, паузы.Минск: Беларуская навука, 2017. 179 с.
- Ефременко Д.С., Кузнецов А.Д., Сероухова О.С. Об одном алгоритме выявления локальных трендов при анализе метеорологических временных рядов// Ученые записки Российского государственного гидрометеорологическогоуниверситета. 2016. № 45. С. 132–141.
- Восканян К.Л., Кузнецов А.Д., Сероухова О.С., Симакина Т.Е. Оценка возможностей метода аналогов для текущего прогноза температуры воздуха// Вестник ТвГУ. Серия: Прикладная математика. 2019. № 1. С. 101–116.https://doi.org/10.26456/vtpmk528
- Восканян К.Л., Кузнецов А.Д., Сероухова О.С., Симакина Т.Е. Текущее прогнозирование экологических измерений на основе поиска аналогов // Сборниктезисов XI научно-прикладной международной конференции «Естественныеи антропогенные аэрозоли» (СПб., 16-18 октября 2018 г.).
- Восканян К.Л., Кузнецов А.Д., Сероухова О.С. Автоматические метеорологические станции. Часть 1. Тактико-технические характеристики: учебное пособие. СПб.: РГГМУ, 2016. 195 с.
- Дьяконов В.П. Справочник по алгоритмам и программам на языке бейсикдля персональных ЭВМ. М.: Наука, 1987. 246 с.