В библиотеку

Анализ алгоритмов шумопонижения в контексте исследования временных рядов

рук.: Анохина И.Ю., исп. Кобец А.А.

ГОУ ВПО «Донецкий национальный технический университет» (г. Донецк)

Источник: Отчет о НИР (заключ.): Донец. нац. техн. ун-т

Анохина И.Ю., Кобец А.А. Анализ алгоритмов шумопонижения в контексте исследования временных рядов В данной работе были исследованы возможности применения алгоритмов шумопонижения при статистическом анализе временных рядов, а также изучения аспектов их использования в данном контексте.

Ключевые слова:временной ряд, шумоподавление, преобразование фурье, вейвлет, трешолдинг

ВВЕДЕНИЕ

При анализе и прогнозировании поведения временных рядов, одной из ключевых задач является минимизация погрешности получаемой модели. В силу хаотической природы временных рядов, данная погрешность неизбежно будет присутствовать при их анализе. В данной работе рассматривается возможность применения алгоритмов шумопонижения для уменьшения влияния нерегулярной составляющей на результаты анализа.

ШУМОПОНИЖЕНИЕ В СТАТИСТИЧЕСКОМ АНАЛИЗЕ

При анализе временных рядов обычно выделяются четыре базовые их составляющие – трендовую, циклическую, сезонную и случайную (нерегулярную, недетерминированную). Считается, что случайная составляющая временного ряда не поддаётся анализу ввиду своей хаотической структуры. Однако взаимодействие детерминированной и случайной составляющих, может негативно сказываться на выявление и анализ первой, увеличивая таким образом погрешность исследований.

Таким образом возникает необходимость уменьшения случайной составляющей временного ряда. Для этих целей можно представить временной ряд как некий сигнал и применить на нём алгоритмы шумопонижения.

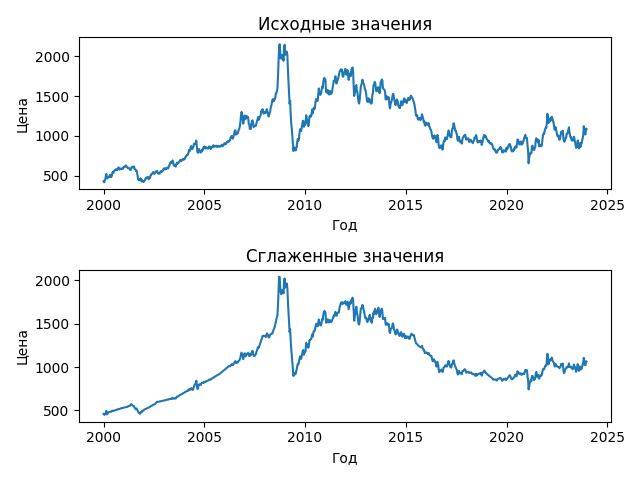
Пример временного ряда до и после применения алгоритмов шумопонижения

Данные алгоритмы позволяют во многом сгладить случайные флуктуации, обусловленные нерегулярной составляющей временного ряда, не затронув при этом детерминированную его часть. Таким образом, возможно значительно уменьшить влияние случайных факторов на результат анализа.

Стоит отметить, что данный подход позволяет лишь уменьшить влияние случайных флуктуаций на итоговый результат, но не обеспечить полное их вычленение. Увеличение же коэффициента чувствительности может в свою очередь затронуть информативную часть графика. Поэтому задача поиска оптимальных его значений при подготовке данных к их дальнейшему статистическому анализу ложится на исследователя.

Наиболее совершенными, алгоритмами для решения задач данного класса являются методы, основывающиеся на техниках спектрального анализа – преобразовании Фурье и вейвлет анализе.

Шумопонижение на основе преобразования Фурье

Преобразование Фурье – это операция, широко применяемая в алгоритмах цифровой обработки сигналов, а также в других областях, связанных с анализом частот в сигналах.

Преобразование Фурье позволяет разложить исходный сигнал на гармонические составляющие, что потребуется для выделения шумов. Выражается данное преобразование следующей формулой:

$\hat{f}\left(\omega\right)= \int_{-\infty}^{+\infty}{f\left(t\right)e^{-i\omega t}dt}$

где $f(t)$ – исходный сигнал (оригинал);

$\hat{f}(\omega)$ – изображение по Фурье;

$\omega$ – частота.

Соответствующее ему обратное преобразование в таком случае будет выглядеть следующим образом:

$f\left(t\right)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}{\hat{f}\left(\omega\right)e^{i\omega t}dt}$

На практике же рассматриваются только конечные последовательности дискретных измерений. Для конечных равномерно распределенных последовательностей применяется применяем дискретное преобразование Фурье (DFT), заданное следующей формулой:

$Y_k=\sum_{n=0}^{N}{X_n\cdot}e^{\frac{-2\pi i}{N}kn}$

где $Y_k$ – $k$-й элемент в векторе дискретного преобразования Фурье;

$X_n$ – $n$-й элемент оригинального вектора;

$N$ – количество элементов в оригинальной временной последовательности.

Сообразно непрерывному варианту, обратное преобразование будет иметь следующий вид:

$X_n=\frac{1}{N}\sum_{k=1}^{N}{Y_k\cdot e^{\frac{2\pi i}{N}kn}}$

Спектральная мощность шума в таком случае будет относительно невелика. Таким образом можно выбрать порог амплитуды, ниже которого будет оставаться случайная составляющая. Используя преобразование Фурье, можно отфильтровать доминирующие компоненты от зашумленных данных. После фильтрации более слабых компонентов, сигнал синтезируется вновь по формуле обратного преобразования Фурье:

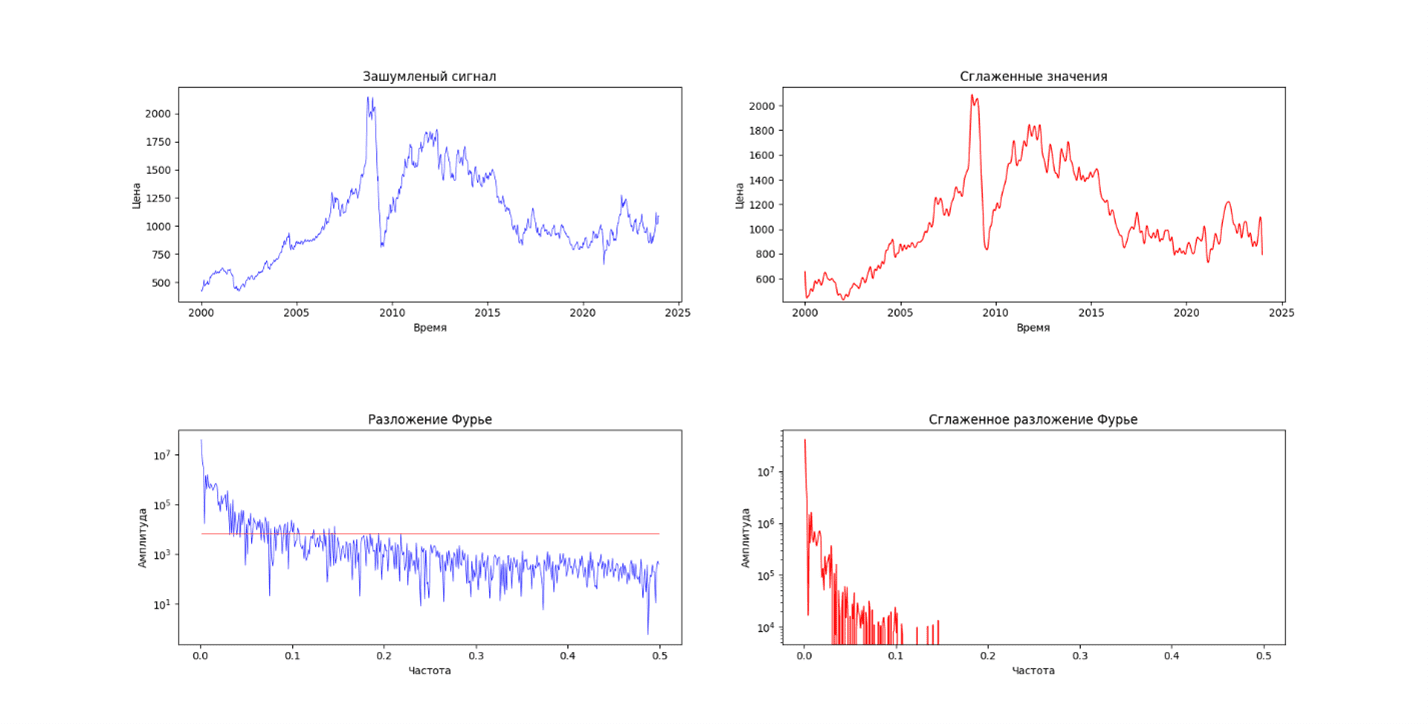
Основные этапы при шумоподавлении.

Преобразования Фурье будет работать очень хорошо, когда частотный спектр стационарный. При этом частоты, присутствующие в сигнале, не зависят от времени, и сигнал содержит частоты, которые присутствуют в любом месте сигнала. Чем нестационарнее сигнал, тем хуже будут результаты. Это проблема, так как большинство сигналов, которые можно наблюдать в реальной жизни, нестационарны по своей природе.

Преобразование Фурье имеет высокое разрешение в частотной области, но нулевое разрешение во временной, что видно на следующих двух примерах:

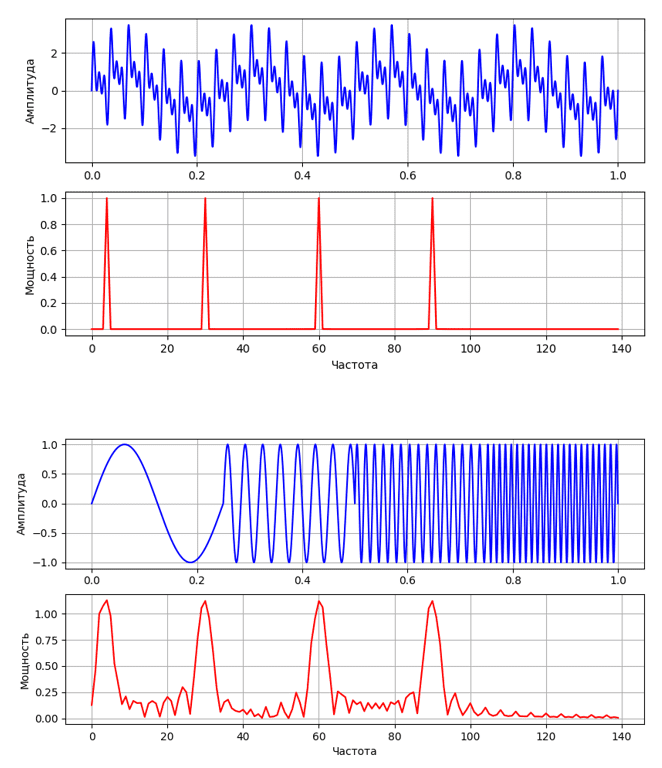
Фурье-преобразование для частот, присутствующих в сигнале в течении всего времени его действия и сигналов, не перекрывающихся во времени.

Для двух частотных спектров, содержащих точно такие же четыре пика, преобразование Фурье не может определить, где в сигнале эти частоты присутствуют. (Боковые лепестки во втором случае обусловлены разрывом между четырьмя различными частотами). Лучшим подходом для анализа сигналов с динамическим частотным спектром является вейвлет-преобразования.

Вейвлет-трешолдинг

Вейвлет — это малая волна, а вейвлет-преобразования преобразуют сигнал в серию всплесков и обеспечивают способ анализа осциллограмм, ограниченных как по частоте, так и по длительности. Это позволяет сохранять сигнал более эффективно, чем преобразование Фурье. Выбор типа, а следовательно, свойств вейвлета, зависит от поставленной задачи и так же определяется исследователем.

Вейвлеты имеют две характеристики – масштабирующий коэффициент и смещение, взаимосвязь между которыми примерно соответствует операции масштабирования. При малых масштабах используются сжатые вейвлеты, они соответствуют быстро меняющимся сигналам (высокочастотным). При больших масштабах вейвлеты растягиваются, они соответствуют медленно меняющимся сигналам (низкочастотным).

Для большинства сигналов их низкочастотная составляющая является наиболее важной частью потому, что с ее помощью можно идентифицировать сигнал. Высокочастотная составляющая в свою очередь несет в себе очертания сигнала. Если в сигнале удалить высокочастотную составляющую, то он поменяется, но основное его поведение останется распознаваемым. Однако если удалить большое количество низкочастотных составляющих сигнала, он станет нераспознаваемым. В вейвлет-анализе приближения исследуются на больших масштабах, низкочастотные составляющие и детализации – на маленьких. Ниже показано разложение сигнала при помощи вейвлет-анализа, где ФНЧ – фильтр низких частот, ФВЧ – фильтр высоких частот, А – приближение, D – детализация:

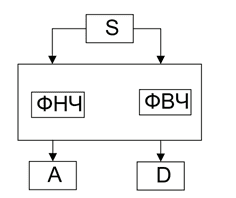
Разложение сигнала при помощи вейвлет-преобразования

Процесс разложения может итеративно повторяться, причем последовательные разложения раскладываются таким образом, что один сигнал дробится на множество сигналов более низкого разрешения. Так как процесс разложения является итеративным, в теории его можно продолжать до бесконечности. На практике процесс можно продолжать до тех пор, пока отдельные детализации состоят из одного образца или пикселя, или же не станут короче длины фильтра.

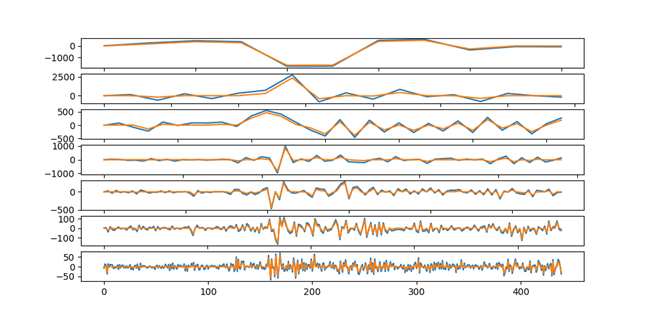
Для шумопонижения в данном методе используется трешолдинг (пороговая обработка данных) – техника исследования сигналов, содержащих шум, осуществляющая декомпозицию исходного сигнала в вейвлет-спектр, который в дальнейшем подвергается обработке. Вейвлет-спектр – функция, содержащая два аргумента (время и масштаб). Результатом дискретного вейвлет-преобразования является N последовательностей, в которых номер – координата масштаба, а номер элемента в последовательности – временная координата:

Далее выбирается некоторое значение коэффициента фильтрации $k$, определяющее степень сглаживания значений и соответствующая ему степень трешолдинга $\Delta$, как правило рассчитывающаяся по формуле:

$\Delta=k\cdot Y_{max}$

где $Y_{max}$ – наибольшее значение амплитуды в спектре.

При мягком трешолдинге полученные значения обрабатываются по формуле

$Y^\prime=\frac{Y}{|Y|}\cdot\max\funcapply(\left|Y\right|-\Delta,0)$

Таким образом, значения меньше $\Delta$ в спектре заменяются на 0, а выше или равные ему – ужимаются в направлении 0 на $\Delta$.

При жёстком трешолдинге, значения меньше $\Delta$ заменяются на 0, а большие значения при этом остаются неизменными.

Пример работы мягкого трешолдинга

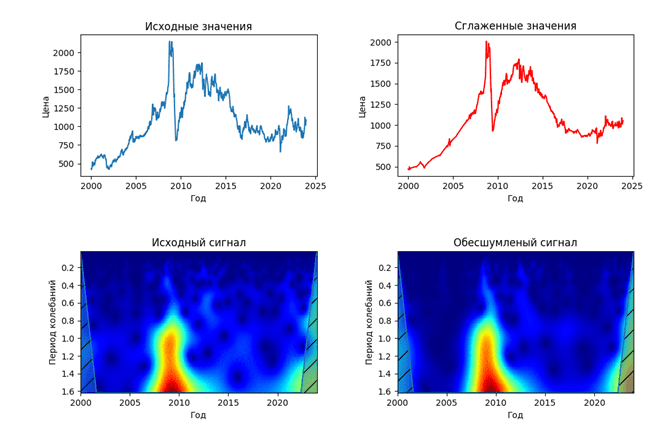
По аналогии с шумоподавлением, основывающимся на преобразовании Фурье, из обесшумленного спектра, ряд синтезируется обратно:

Пример шумоподавления, основанного на вейвлет преобразовании

ЗАКЛЮЧЕНИЕ

В данной работе были рассмотрены некоторые виды алгоритмов шумопонижения в контексте анализа временных рядов, были выделены и исследованы основные аспекты, возникающие при их применении для подготовки данных к дальнейшему анализу. Представленные в настоящей работе технологии шумопонижения являются перспективными методами, способными дополнить традиционные подходы в статистическом анализе временных рядов.

Представленные результаты позволяют выделить ряд направлений для дальнейших исследований — например, подбор базовых функций и типов преобразований (и их комбинаций) при вейвлет трешолдинге для решения традиционных задач; поиск способа подбора оптимальных значений коэффициентов предварительного шумопонижения.

Список использованных источников