Аннотация
Дистрибьюторы товаров должны учитывать ограничения по загрузке, чтобы реалистично планировать работу своих транспортных средств, в то время как существующие инструменты планирования обычно не включают эти ограничения. Наиболее распространенными проблемами погрузки, возникающими при распределении товаров, являются многомерные ограничения на упаковку, ограничения на последовательность разгрузки, ограничения на устойчивость и ограничения на вес оси. В данной работе проблемы маршрутизации транспортных средств объединены с проблемами погрузки. Во-первых, представлен обзор соответствующей литературы. Во-вторых, в статье проливается свет на ограничения веса осей, поскольку, насколько нам известно, VRP с ограничениями веса осей еще не рассматривались в литературе. Формулируется двумерная модель VRP с последовательной загрузкой. Эта модель используется для проведения вычислительных экспериментов на небольшой сети. Для каждого рассчитанного маршрута транспортного средства вычисляется вес на осях и сравнивается с законодательными ограничениями.
Ключевые слова: задача маршрутизации транспортных средств, ограничения на загрузку, вес на осях, двумерная VRP
1. ВВЕДЕНИЕ
Задача маршрутизации транспортных средств (VRP) касается распределения товаров между складами и клиентами (Toth and Vigo, 2002). Это наиболее часто изучаемая задача комбинаторной оптимизации в области транспорта и логистики. Цель задачи маршрутизации транспортных средств состоит в том, чтобы найти набор маршрутов для парка транспортных средств, при которых целевая функция (например, общее расстояние, затраты на маршрутизацию) оптимизирована. Необходимо удовлетворять каждое требование и учитывать вместимость транспортных средств. Базовой версией VRP является емкостный VRP (CVRP). CVRP рассматривает однородный автопарк с фиксированной вместимостью (по весу или количеству единиц), который доставляет товары с одного склада в пункты расположения клиентов. Раздельные поставки не допускаются. CVRP может быть расширен до VRP с временными окнами (VRPTW), указав временные окна, в которые должны осуществляться поставки. Другим вариантом является VRP с приемом и доставкой (VRPDP), в котором заказы могут забираться и доставляться в места расположения клиентов. Для каждого заказа указывается местоположение отправителя (место получения) и место назначения (место доставки). Возможна как доставка, так и самовывоз в заданном месте. Третьим распространенным дополнением к базовому CVRP является VRP с обратными перевозками (VRPB), в котором снова прием и доставка могут осуществляться в течение одного тура, но сначала необходимо выполнить все запросы на доставку, а затем пустой автомобиль может забрать товар в местах расположения клиентов. (Toth and Vigo, 2002)
Для "классических" VRP, упомянутых в предыдущем абзаце, уже существует множество методов решения. В реальной жизни компании сталкиваются с несколькими дополнительными ограничениями, которые значительно усложняют проблему. Примерами таких усложняющих ограничений являются максимальная протяженность и продолжительность маршрута, зависящий от времени маршрут, несовместимость товаров и транспортных средств и ограничения по загрузке. "Богатые" VRP - это задачи маршрутизации, которые учитывают некоторые из этих дополнительных реалистичных ограничений (Баттарра, Моначи и Виго, 2009). В этой статье основное внимание уделяется проблемам маршрутизации в сочетании с ограничениями загрузки.
Опрос, проведенный авторами среди нескольких бельгийских поставщиков логистических услуг, показал, что они сталкиваются с серьезными проблемами погрузки при планировании маршрутов. Наиболее распространенными проблемами при погрузке, с которыми сталкиваются дистрибьюторы, являются ограничения по многомерности упаковки, последовательности разгрузки, устойчивости, прочности на растяжение и весу оси. Ограничения по многомерности упаковки включают в себя то, что товары не могут накладываться друг на друга и должны быть полностью закрыты транспортным средством. В трехмерной задаче для проверки этого ограничения принимаются во внимание три измерения (длина, ширина и высота) транспортного средства. В одномерной или двумерной задаче учитываются, соответственно, одно или два измерения транспортного средства. Ограничение последовательности разгрузки гарантирует, что при прибытии к клиенту никакие товары, принадлежащие клиентам, обслуживаемым позже по маршруту, не препятствуют вывозу товаров текущего клиента. В одномерной задаче это ограничение можно обозначить как ограничение "Последний входит первым выходит" (LIFO). Ограничения устойчивости гарантируют как вертикальную, так и горизонтальную устойчивость груза в транспортном средстве. Когда предметы укладываются в транспортном средстве друг на друга, они должны поддерживаться другими предметами или полом, чтобы обеспечить вертикальную устойчивость груза. Ограничения вертикальной устойчивости определяют минимальную площадь опоры каждого предмета (например, в процентах от площади основания предмета). устойчивость груза относится к поддержке боковых сторон предметов в транспортном средстве во избежание перемещения предметов в транспортном средстве. Несущая способность изделия - это максимальное давление, которое может быть приложено к данному изделию (Junqueira et al., 2012). Это учитывается для предотвращения повреждения изделий из-за давления других предметов, расположенных над ними. Хрупкие предметы можно определить как предметы, которые не выдерживают большого давления. Это может означать, что ни один предмет нельзя класть на хрупкие предметы или что на них можно класть только другие хрупкие предметы. Важен не только общий вес груза внутри транспортного средства, но и распределение веса этого груза по осям транспортного средства. Ограничения по весу осей создают серьезную проблему для транспортных компаний. Перевозчикам грозят высокие штрафы за нарушение этих ограничений, в то время как текущие программы планирования не предусматривают ограничений по весу оси. Законодательство об ограничениях по весу оси варьируется в зависимости от страны (обзор ограничений по весу оси в Европе можно найти на Международном транспортном форуме). Вес на оси - это общий вес, который размещается на осях грузовика или прицепа. Это проиллюстрировано на рисунке 1. Когда изделие j размещается на транспортном средстве, вес изделия распределяется по осям грузовика и прицепа. представляет вес товаров клиента j, размещенных на осях грузовика. представляет вес товаров клиента j, размещенных на осях прицепа.
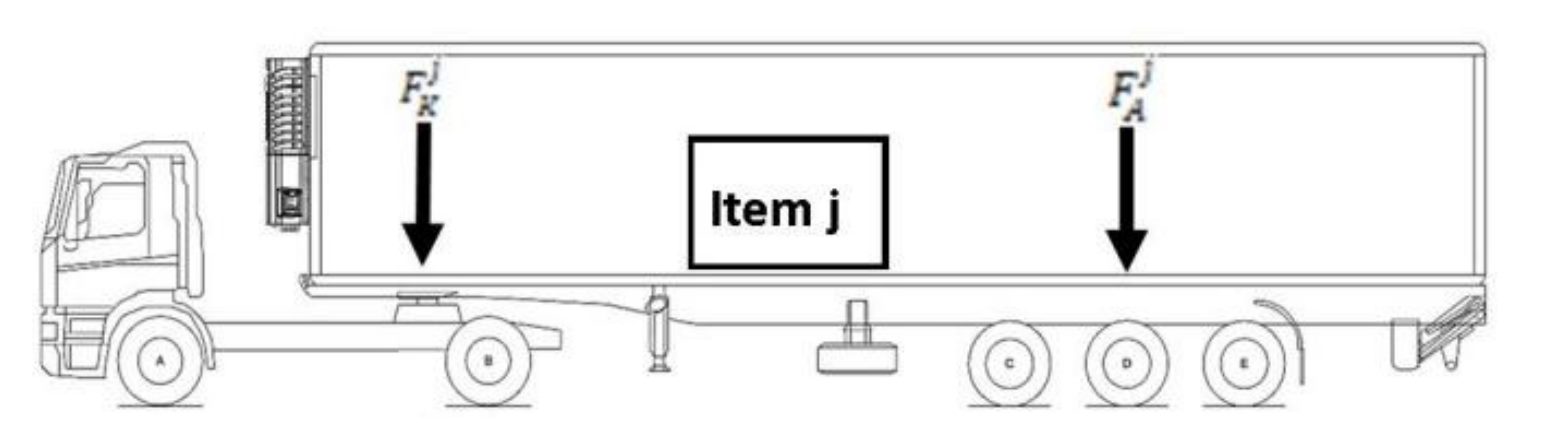
Рисунок 1 - Грузовой автомобиль с грузоподъемностью на ось и прицеп
Основная цель статьи - продемонстрировать необходимость учета ограничений по весу оси в модели VRP. В разделе 2 представлен обзор литературы, касающейся VRP в сочетании с ограничениями по нагрузке. Двумерный CVRP сформулирован в разделе 3. В разделе 4 модель используется для проведения вычислительных экспериментов на небольшой сети. Для каждого рассчитанного маршрута транспортного средства рассчитывается вес на осях и сравнивается с допустимыми ограничениями. В последнем разделе обсуждаются выводы и возможности будущих исследований.
2. ИЗУЧЕНИЕ ЛИТЕРАТУРЫ
Сочетание проблем VRP и загрузки является довольно недавней областью исследований. Эти две проблемы по отдельности уже являются NP-сложными и очень трудноразрешимыми (Iori and Martello 2010). Таким образом, объединение этих проблем является очень сложной задачей, но приводит к лучшему общему логистическому решению. Статьи, посвященные VRP с проблемами загрузки, могут быть отнесены к следующим категориям в зависимости от типа проблемы маршрутизации и характеристик загрузки, которые рассматриваются: VRP и 2D загрузка, VRP и 3D загрузка, VRP с несколькими штабелями, многокомпонентная VRP и PDP с ограничениями загрузки. В этой статье мы сосредоточимся на общих VRP, при которых все товары забираются на складе и затем доставляются клиентам. Поэтому мы не будем вдаваться в подробности о PDP. Для получения подробного обзора литературы по этой теме вплоть до 2010 года читатель может обратиться к Иори и Мартелло (2010).
2.1. VRP с двухмерными ограничениями нагрузки В двумерном VRP требования клиентов и размеры транспортного средства выражаются в двух измерениях
Иори, Салазар-Гонсалес и Виго (2007) первыми обратились к двумерной задаче маршрутизации транспортного средства. Они разработали точный метод решения проблемы, который учитывает загрузку на основе последовательности, фиксированные ограничения ориентации и максимальную грузоподъемность. Общие затраты на маршрутизацию сводятся к минимуму с помощью метода ответвлений и исходящих сообщений. Гендро и др. (2008) разрабатывают метод поиска по табу (TS) для эвристического решения той же проблемы. Fuellerer et al. (2009) используют метод оптимизации колонии муравьев (ACO) для аналогичной задачи с небольшим изменением ограничений на загрузку. В своей модели элементы могут поворачиваться на 90° в горизонтальной плоскости. Захариадис, Тарантилис и Кираноудис (2009) разрабатывают метод управляемого поиска по табу, который представляет собой комбинацию управляемого локального поиска и TS для решения задачи 2L-CVRP, сформулированной Iori et al. (2007). Дюамель и др. (2011) обращаются к 2L-CVRP без загрузки на основе последовательности, используя жадную процедуру рандомизированного адаптивного поиска (GRASP) в рамках эволюционного локального поиска (ELS). Леунг и др. (2013) разработали модель имитационного отжига (SA) для решения задачи 2L-CVRP с гетерогенным парком. Ограничения по упаковке, которые учитываются в этой модели, такие же, как в Iori et al. (2007). Транспортные средства имеют разную грузоподъемность и разные размеры. В настоящее время это единственный многомерный CVRP, в котором рассматривается разнородный автопарк.
2.2. VRP с трехмерными ограничениями по загрузке
В 3L-CVRP учитываются три измерения транспортного средства, а требования заказчика также состоят из трехмерных элементов. Поскольку учитывается размер по высоте, могут быть указаны дополнительные ограничения по нагрузке, касающиеся несущей способности и устойчивости груза.
Гендро и др. (2006) первыми взялись за решение проблемы маршрутизации трехмерного транспортного средства с емкостью (3L-CVRP). Они разрабатывают метод TS для решения проблемы с целью минимизации общей длины маршрута. Их модель учитывает последовательность загрузки, грузоподъемность транспортного средства, ограничения по хрупкости и устойчивости, а также фиксированную вертикальную ориентацию предметов в транспортных средствах (допускается поворот предметов на 90° в плоскости ширина-длина).
В нескольких работах учитываются те же ограничения нагрузки, что и в Gendreau et al. (2006) для решения CVRP (например, Ren, Tian и Sawaragi 2011; Ruan et al. 2013; Бортфельдт и Хомбергер 2013).
Moura (2008) разрабатывает многоцелевой генетический алгоритм для решения задачи 3L-CVRP с временными окнами (3L-VRPTW). Модель учитывает загрузку на основе последовательности, ограничения ориентации и стабильности. Представленная задача преследует три цели: минимизация количества транспортных средств, минимизация общего пройденного расстояния и максимизация использования объема. В 2009 году Моура и Оливейра разработали последовательный и иерархический подход к решению проблемы 3L-VRPTW. Цель состоит в том, чтобы свести к минимуму количество транспортных средств и общее время прохождения маршрута. Иерархический подход учитывает загрузку на основе последовательности, ограничения ориентации и устойчивости. При последовательном подходе загрузка контейнеров и маршруты движения транспортных средств планируются одновременно. При таком подходе к решению ограничение последовательности разгрузки ослаблено.
Массен, Девилл и Ван Хентенрик (2012) разрабатывают метод генерации столбцов для задач маршрутизации транспортных средств с реализуемостью "черного ящика" (VRPBB). В VRPBB маршруты базового VRP должны удовлетворять ряду неизвестных ограничений. Алгоритм черного ящика используется для проверки выполнимости маршрута. Их подход протестирован на 3L-CVRP, а также на multiple pile-VRP.
Жункейра, Оливейра и Морабито (2012) первыми предложили точный метод решения задачи 3L-CVRP. Они учитывают нагрузку на основе последовательности, ограничения ориентации и устойчивости. Авторы вводят ограничения на многократную выгрузку, которые учитывают схему разгрузки. Задавая длину досягаемости рабочего или вилочного погрузчика, они избегают того, чтобы предметы, расположенные поверх других предметов, не могли быть доставлены. Они предлагают модель целочисленного линейного программирования для решения задач среднего размера
2.3. VRP с несколькими сваями
Задача маршрутизации транспортных средств с несколькими штабелями (VRP) представлена Доэрнером и др. (2007). Они разрабатывают метод TS и эвристику ACO для решения реальной транспортной проблемы, связанной с транспортировкой древесно-стружечных плит. Проводится различие между мелкими и крупными древесностружечными плитами. Для каждого заказа древесностружечные плиты одного типа группируются в уникальный товар, который помещается на одну поддону. Транспортное средство разделено на три штабеля, в которые поддоны могут быть уложены штабелями. Поддоны, содержащие крупногабаритные древесностружечные плиты, могут располагаться на нескольких штабелях. Остальные поддоны можно сложить в одну стопку. Пример схемы погрузки транспортного средства с несколькими штабелями можно найти на рисунке 2.
Из-за такой специфической конфигурации поддонов, размещенных в несколько штабелей, исходная трехмерная задача может быть сведена к одномерной. В модели Doerner et al. (2007) учитывается загрузка на основе последовательности и предполагается однородный парк транспортных средств.
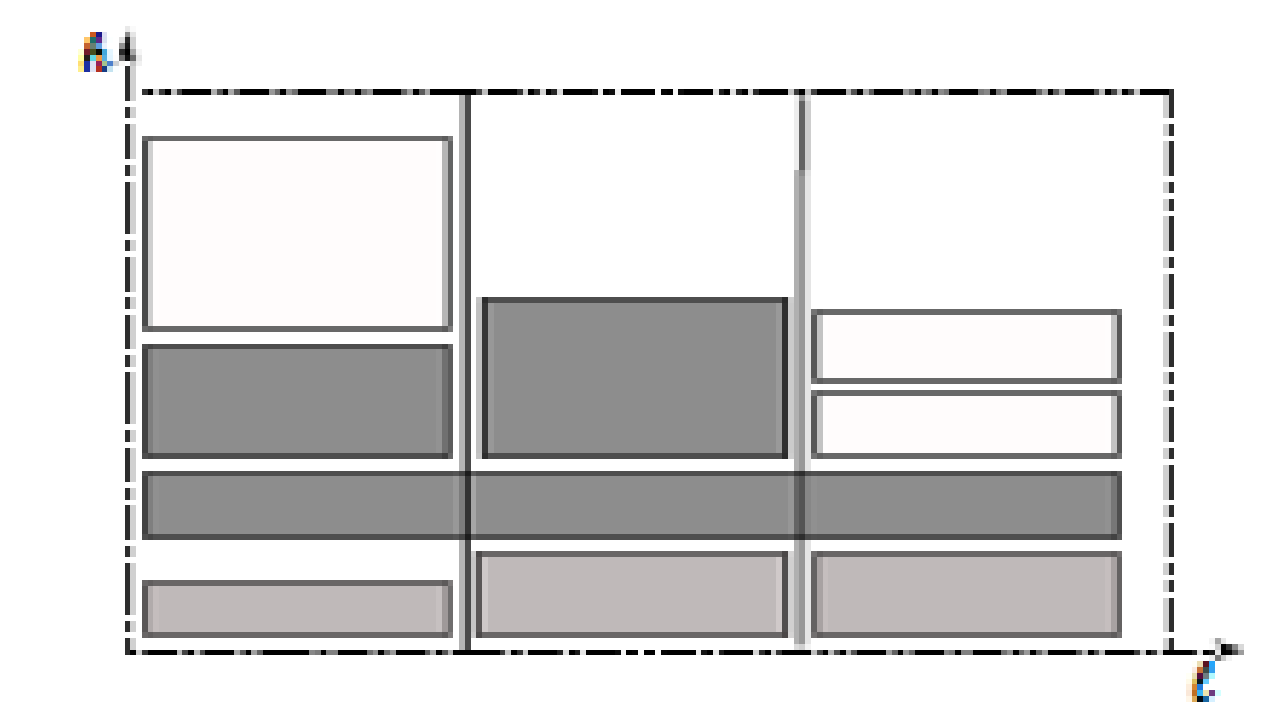
Рисунок 2 - Пример транспортного средства с несколькими сваями (Массен и др., 2012)
Tricoire et al. (2011) разработали комбинацию поиска по переменной окрестности и ветвления и разрезания, чтобы решить MP-VRP точно для экземпляров малого размера и эвристически для экземпляров большого размера. В обоих решениях учитывается загрузка на основе последовательности. Мэдсен и др. (2012) тестируют метод генерации столбцов для задач маршрутизации транспортных средств с реализуемостью черного ящика (VRPBB) на MP-VRP. Они учитывают загрузку на основе последовательности и предполагают однородный автопарк.
2.4. Многокамерная VRP
VRP с несколькими отсеками связан с VRP с несколькими штабелями. Транспортные средства с несколькими отсеками позволяют перевозить неоднородные продукты в одном транспортном средстве, но в разных отсеках. Отсеки не всегда совместимы со всеми типами продуктов, и некоторые пары продуктов нельзя загружать вместе в одни и те же отсеки. Проблемы с маршрутизацией транспортных средств с отсеками встречаются в нескольких отраслях, таких как распределение бензина (например, Brown and Graves 1981; Cornillier et al., 2012), распределение продуктов питания (например, Chajakis and Guignard 2003) и сбор отходов (например, Мюлдерманс и Панг, 2010).
3. ПОСТАНОВКА ЗАДАЧИ
Мы начинаем с исследования классического двумерного CVRP с загрузкой на основе последовательности, тогда как в дальнейших исследованиях выводы могут быть проверены на более сложных VRP. Рассматривается несколько однородных транспортных средств. Грузоподъемность транспортного средства выражается как в грузоподъемности Qk (максимум 30 тонн), так и в максимальной длине Li и ширине Wi погрузочного пространства (10 м и 2 м соответственно). Спрос клиентов состоит из поддонов размером 1х1 метр. Поддоны нельзя класть друг на друга, но их можно разместить рядом в транспортном средстве. В общей сложности внутри каждого транспортного средства можно разместить 20 поддонов.
Рассмотрим полный ориентированный граф, где - множество вершин, соответствующих начальному депо (узел 1), конечному депо (узел n) и клиентам (узел 2 ... n-1). - множество ребер, где каждое ребро имеет соответствующую транспортную стоимость , для . Пусть это набор идентичных транспортных средств. У каждого клиента есть потребность в поддонах. Общий вес в килограммах поддонов, заказанных каждым клиентом, выражается как . Этапы включены в модель, чтобы знать, в какой последовательности посещаются места. Таким образом, мы можем рассчитать вес осей на следующем шаге. Это обозначение также используется Junqueira et al. (2012). Переменные решения о маршрутизации в модели определяются как
Модель маршрута транспортного средства может быть сформулирована следующим образом:
(1)
При условии:
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
Целевая функция (1) направлена на минимизацию общих затрат транспортных средств на посещение всех клиентов. Ограничения (2) и (3) гарантируют, что каждого клиента посетят ровно один раз. Ограничение (4) гарантирует, что каждое транспортное средство может посещать только одну дугу на этапе, в то время как ограничение (5) не позволяет транспортному средству посещать клиента на этапе t, если транспортное средство не посещало клиента на этапе t-1. Ограничение (6) не позволяет общему весу груза превышать грузоподъемность транспортного средства. Ограничение (7) ограничивает количество поддонов на транспортное средство длиной транспортного средства, умноженной на два, поскольку в транспортном средстве можно разместить два поддона рядом друг с другом. Ограничение (8) исключает возможность дополнительных поездок
4. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
Модель, сформулированная в предыдущем разделе, используется для проведения вычислительных экспериментов в небольшой сети. Эта сеть состоит из десяти узлов: начального хранилища (узел 1), клиентов (узлы со 2 по 9) и конечного хранилища (узел 10). Спрос клиентов (узлы со 2 по 9) является постоянным = (8, 4, 2, 6, 4, 6, 8, 10). Чтобы определить границу количества этапов, мы рассчитали количество этапов, необходимое для перевозки клиентов с наименьшим количеством товаров в одном транспортном средстве. Максимум четыре клиента могут обслуживаться одним транспортным средством, а именно клиенты 2, 3, 4 и 5. Общее количество паллет у этих клиентов составляет 16, что ниже максимальной вместимости в 20 паллет. Это означает, что можно установить максимальную границу в 6 этапов (также учитываются начальный и конечный склады). Модель решена с помощью Cplex 12.5 на персональном ноутбуке.
Модельное решение содержит три маршрута движения транспортного средства. Для каждого маршрута движения транспортного средства вес паллет клиента j на прицепе () и на грузовом автомобиле рассчитывается с помощью уравнений (10) и (11) соответственно. На рисунке 3 параметры в уравнениях представлены графически. Параметр представляет расстояние от начала прицепа до центра тяжести изделия. Параметр f обозначает расстояние от начала прицепа до сцепного устройства (которое является связующим звеном между грузовиком и прицепом). Последний параметр d представляет собой расстояние между сцепным устройством и средними осями прицепа. Для наших расчетов мы используем 1,67 м для параметра c и 7,8 м для параметра d
(10)
(11)
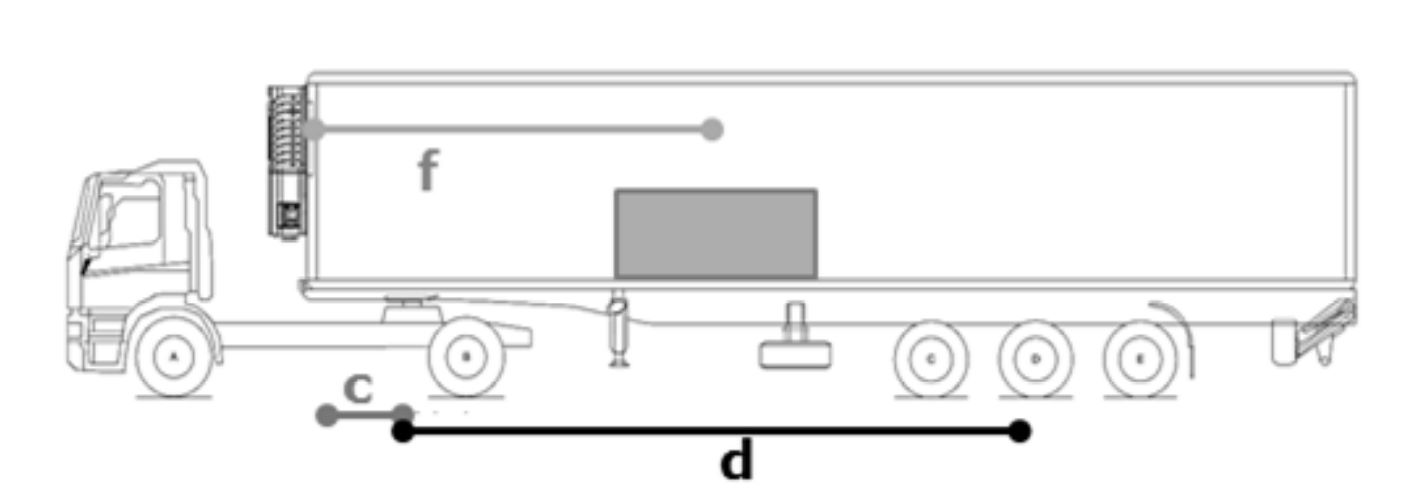
Рисунок 3 - Грузовик (с двумя осями) и прицеп (с тремя осями)
Согласно бельгийскому законодательству, максимальный общий вес на двух осях этого грузовика составляет 22 тонны. Пустой грузовик весит 8 тонн, следовательно, максимальный вес груза на осях грузовика составляет 14 тонн (или 14000 кг), как указано в ограничении (12).
(12)
Бельгийское законодательство ограничивает максимальный вес прицепа с осями tridem до 30 тонн. Пустой прицеп весит 14 тонн. Таким образом, вес груза на осях прицепа ограничен 16 тоннами (или 16000 кг), как указано в ограничении (13).
(13)
Грузоподъемность транспортного средства составляет 30 тонн. Это равно сумме предельных значений веса осей грузовика и прицепа. Таким образом, мы можем сделать вывод, что при оптимальном распределении нагрузки по осям транспортного средства вес груза может составить 30 тонн. В таблицах 1, 2 и 3 представлены расчеты веса оси грузовика и прицепа транспортного средства соответственно по первому, второму и третьему маршруту. В первом столбце указаны узлы клиентов, которые посещаются в ходе маршрута. Во втором столбце представлен потребительский спрос, деленный на два, что равно общему количеству счетчиков загрузки, требуемому клиентом j. Для простоты расчетов мы предположили, что потребительский спрос является равномерным. Это ограничение можно легко ослабить. В третьей колонке представлено расстояние от начала прицепа до центра тяжести поддонов клиента j. Предполагается, что центр тяжести каждого поддона находится в середине поддона. В следующем столбце представлен вес поддонов в килограммах каждого клиента j. В пятом столбце рассчитан вес товаров клиента j на осях прицепа. В последней колонке представлен вес товаров клиента j на осях грузовика. В последней строке представлена сумма показателей погрузки, веса поддонов, веса оси прицепа и веса оси грузовика для каждого маршрута
Из таблицы 1 можно сделать вывод, что, хотя общий вес транспортного средства (18 тонн) все еще значительно ниже грузоподъемности транспортного средства (30 тонн), а также при соблюдении габаритов транспортного средства по длине (<10m) налицо нарушение ограничения по весу оси грузовика, поскольку оно превышает 14 тонн. Аналогичные результаты можно получить из таблиц 2 и 3. В этом примере ограничение по весу оси грузовика нарушено для каждого транспортного средства. Однако – хотя это и не проиллюстрировано в данном примере – также возможно нарушение предельного веса прицепа на оси или (в идеальном случае) соблюдение обоих ограничений.
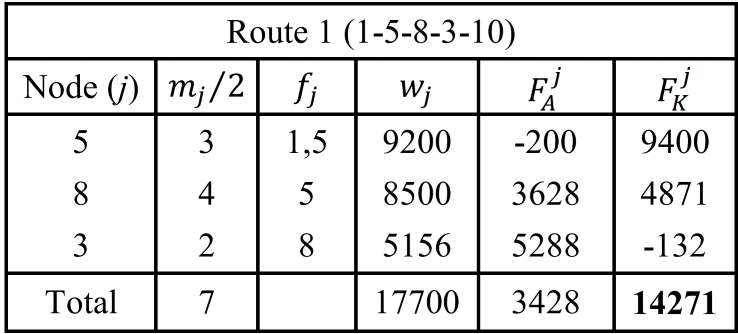
Таблица 1 - Расчет веса оси прицепа (F_A) и грузовика (F_K) маршрут движения транспортного средства 1
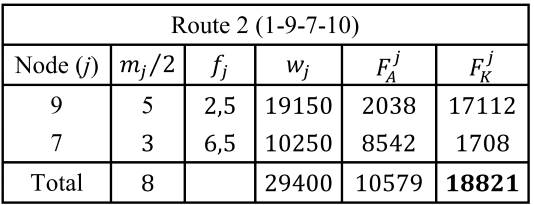
Таблица 2 - Расчет веса оси прицепа (F_A) и грузового автомобиля (F_K) маршрут 2
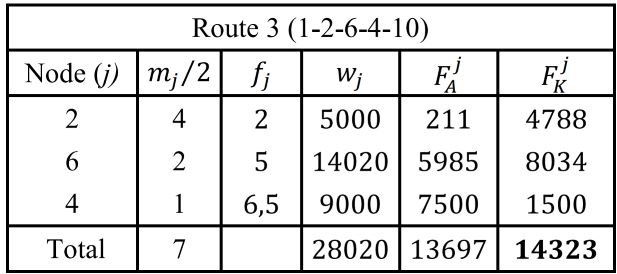
Таблица 3 - Расчет веса оси прицепа (F_A) и грузовика (F_K) маршрут транспортного средства 3
ВЫВОДЫ И БУДУЩИЕ ИССЛЕДОВАНИЯ
В этой статье показана необходимость интеграции ограничений по весу оси в модели VRP. Хотя были проведены исследования по VRP в сочетании с ограничениями по нагрузке, в литературе по-прежнему ничего не говорится об ограничениях по весу оси. Однако вес оси становится все более важной проблемой для транспортных компаний. Перевозчики сталкиваются с высокими штрафами за нарушение этих ограничений, в то время как текущие программы планирования не учитывают эти ограничения. Будущие исследования могут включить ограничения по весу оси в модель. Это может включать в себя учет ограничений по весу на оси при полной загрузке транспортного средства и увеличение веса на оси при доставке товаров в пункты обслуживания клиентов. Впоследствии может быть разработан эвристический метод для решения комплексной проблемы в приемлемые сроки. Наконец, в модель могут быть добавлены другие реалистичные ограничения, такие как временные окна и трехмерная загрузка.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
- Aprile, D., Egeblad, J., Garavelli, A.C., Lisi, S., Pisinger, D, 2007. Logistics optimization: vehicle routing with loading constraints. Proceeding of 19th International Conference on Production Research. July 29 - August 2, 2007, Chile.
- Battarra, M., Monaci, M., Vigo, D., 2009. An adaptive guidance approach for the heuristic solution of a minimum multiple trip vehicle routing problem. Computers & Operations Research, 36(11): 3041 – 3050.
- Bortfeldt, A., Homberger, J., 2013. Packing first, routing second a heuristic for the vehicle routing and loading problem. Computers & Operations Research, 40(3), 873–885.
- Brown, G.G., Graves, G.W., 1981. Real-time dispatch of petroleum tank trucks. Management Science, 27(1):19-32.
- Chajakis, E.D., Guignard, M., 2003. Scheduling deliveries in vehicles with multiple compartments. Journal of Global Optimization, 26(1):43-78.
- Cornillier, F., Boctor, F., Renaud, J., 2012. Heuristics for the multi-depot petrol station replenishment problem with time windows. European Journal of Operational Research, 220(2):361-369.
- Doerner, K., Fuellerer, G., Hartl, R., Gronalt, M., Iori, M., 2007. Metaheuristics for the vehicle routing problem with loading constraints. Networks, 49(4): 294 – 307.
- Duhamel, C., Lacomme, P., Quilliot, A., Toussaint, H., 2011. A multi-start evolutionary local search for the two-dimensional loading capacitated vehicle routing problem. Computers & Operations Research, 38(3): 617 – 640.
- Fuellerer, G., Doerner, K.F., Hartl, R.F., and Iori, M., 2009. Ant colony optimization for the two- dimensional loading vehicle routing problem. Computers & Operations Research, 36(3):655 – 673.
- Gendreau, M., Iori, M., Laporte,G., Martello, S., 2006. A tabu search algorithm for a routing and container loading problem. Transportation Science, 40(3): 342 – 350.
- Gendreau, M., Iori, M., Laporte,G., Martello, S., 2008. A tabu search heuristic for the vehicle routing problem with two-dimensional loading constraints. Networks, 51(1):4 – 18.
- Iori, M., Martello, S., 2010. Routing problems with loading constraints. TOP, 18(1):4 – 27
- Iori, M., Salazar-Gonzalez, J.S., Vigo, D., 2007. An exact approach for the vehicle routing problem with two-dimensional loading constraints. Transportation Science, 41(2):253 – 264.
- Junqueira, L., Oliveira, J.F., Carravilla, M.A., Morabito, R., 2012. An optimization model for the vehicle routing problem with practical three-dimensional loading constraints. International Transactions in Operational Research, forthcoming (DOI: 10.1111/j.1475-3995.2012.00872.x)
- Leung, S.C., Zhang, Z., Zhang, D., Hua, X., Lim, M.K., 2013. A meta-heuristic algorithm for heterogeneous fleet vehicle routing problems with two- dimensional loading constraints. European Journal of Operational Research, 225(2):199 – 210.
- Massen, F., Deville, Y., Van Hentenryck, P., 2012. Pheromone-based Heuristic Column Generation for Vehicle Routing Problems with Black Box Feasibility. Proceeding of the International Conference on Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems (CPAIOR), 260 – 274. May 28 – June 1, Nantes, France.
- Moura, A., 2008. A multi-objective genetic algorithm for the vehicle routing with time windows and loading problem. In Bortfeldt, A., Homberger, J., Kopfer, H., Pankratz, G., Strangmeier, R., eds. Intelligent Decision Support, Current Challenges and Approaches. Wiesbaden, Germany. Gabler, 187-201.
- Moura, A., Oliveira, J., 2009. An integrated approach to the vehicle routing and container loading problems. OR Spectrum, 31(4):775 – 800.
- Muyldermans, L., Pang, G.,2010. A guided local search procedure for the multi compartment capacitated arc routing problem. Computers & Operations Research, 37(9):1662-1673.