Аннотация
А. В. Обухова. Численное моделирование электромагнитных и тепловых нолей в устройствах индукционной плавки Разработана двумерная конечно-элементная модель для электромагнитных и тепловых процессов в устройствах индукционной плавки.
Исследуемая индукционная система состоит из многовитковых индуктирующих обмоток, питаемых от внешних источников переменного тока, и нагреваемой заготовки конической формы. Математическая модель этой системы может быть построена без существенных погрешностей с учетом следующих допущений:
- пространственная конфигурация системы позволяет ограничиться рассмотрением двумерной осесимметричной области (К-2);
- поле полагается квазистационарным, низкая частота внешнего тока (?=50Гц) позволяет пренебречь токами смещения по сравнению с токами в проводящих телах;
- не учитываются потери на гистерезис при нагреве ферромагнитных тел в силу их незначительности по сравнению с потерями от вихревых токов.
Исходная постановка нелинейной электромагнитной задачи с учетом сделанных допущений выражается через векторный потенциал общим уравнением Пуассона [2] в двумерной осесимметричной области У(х,г):
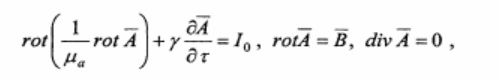
где А - векторный магнитный потенциал; 10 - плотность тока внешних источников; В - магнитная индукция; |іа - абсолютная магнитная проницаемость среды; у - удельная электрическая проводимость.
Принимая во внимание осевую симметрию и квазистационарность исследуемого поля, уравнение(І) можно представить для комплексной амплитуды векторного потенциала в виде
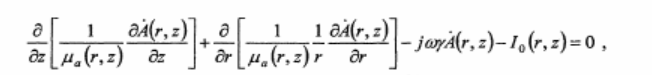
где (0=27^ - циклическая частота питающего тока, у = V— 1 - мнимая единица.
В качестве граничных условий для определенности задачи примем наиболее общие условия - равенство нулю векторного потенциала на границе расчетной области (2, находящейся в бесконечности. В реальной ситуации граница расчетной области удалена от источников тока так, что магнитную энергию поля можно принять равной нулю. Рассматриваемая область (5 имеет границы 81 и 82, на которых задаются граничные условия:
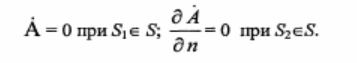
Основной особенностью индукционного нагрева является выделение тепла в самих нагреваемых телах. Это позволяет передавать в них большие мощности, получать высокие термические КПД за счет выделения теплоты только в требуемых частях объемов. Температурное поле в твердом теле описывается уравнением теплопроводности
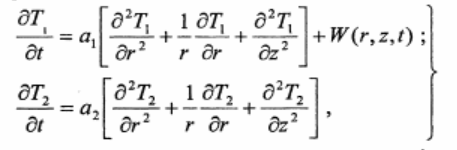
где Т- температура, а- коэффициент температуропроводности, а = А ; А,- коэффициент теплопроводенности; у-плотность материала; тепловой поток с поверхности заготовки; \У(г, г, 1)- функция распределения внутренних источников тепла.
Для полного описания процесса нагрева необходимо знать краевые условия (начальные и граничные), которые имеют вид
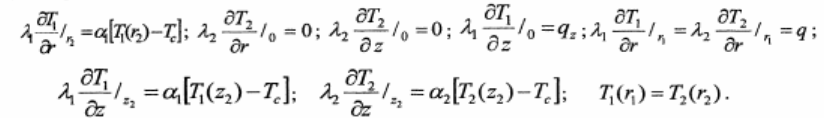
Сложность формы заготовки не позволяет получить точное аналитическое выражение для температурного поля, поэтому более приемлемым путем решения такой задачи является применение численных методов. Особенно эффективен при решении задач в областях с криволинейными границами метод конечных элементов (МКЭ) [3-4].
Сущность подхода, основанного на МКЭ, заключается в исследовании глобальной функции процессов в дискретных частях анализируемой области, которая должна быть предварительно разбита на конечные смежные подобласти (конечные элементы (КЭ)), что позволяет свести исходную задачу с бесконечным числом степеней свободы к задаче, содержащей конечное число неизвестных параметров. При этом внутри подобластей искомая функция интерполируется степенными полиномами, сшивается на границах контакта элементов и при условии малости геометрических размеров последних (число элементов стремится к бесконечности) оказывается решением уравнений в частных производных типа (1 Невысокая инерционность тепловых процессов в сравнении с электромагнитными позволяет решать эти задачи раздельно.
Следуя МКЭ системе уравнений (1) и дифференциальным уравнениям (4), ставят в соответствие функционалы вида:
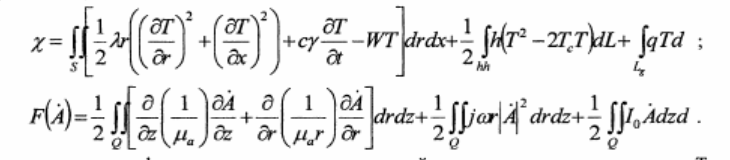
Соответствующие функционалы заменяются суммой вкладов отдельных элементов. Таким образом определяется функциональное соотношение относительно узловых неизвестных. В качестве элементов выбирались треугольные симплекс-элементы. Затем определяются вклады элементов в матрицы жесткости, матрицы демпфирования и в вектор источников энергии и тепла. Вклады элементов объединяются в глобальные матрицы, которые характеризуют поведение дискретной системы в целом. Этот процесс, который осуществляется с помощью процедуры поэлементного объединения получил название ансамб-лирования элементов. Полученные матрицы объединяют в систему алгебраических уравнений с комплексными коэффициентами
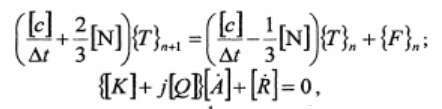
где[С],[К]-матрицы жесткости; [^-матрица демпфирования; {Т}-матрица базисных функций; {Бивектор источников тепла; [(}]-матрица вихревых токов; [11]-матрица внешних источников тока.
Решение системы уравнений (8), (9) осуществляется с помощью стандартной процедуры Ы)ЬТ-факторизации. Эта процедура выполняется всего за два шага. Первый шаг заключается в вычислении коэффициентов диагональной матрицы и нижней треугольной матрицы. На втором шаге процедуры сразу определяются искомые функции для температурного и магнитного полей в узлах расчетных сеток КЭ.
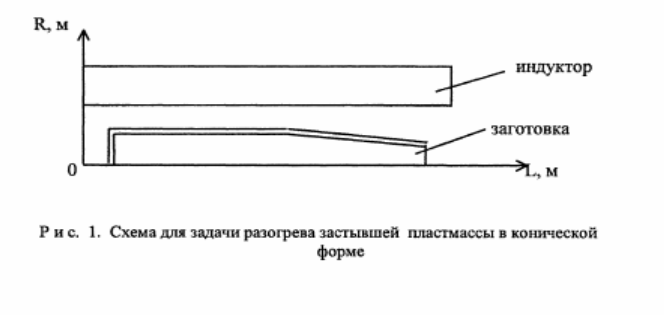
По полученной модели был проведен ряд исследований для задачи разогрева застывшей пластмассы в объеме конической формы до момента отлипания пограничного слоя от стенок формы (рис.1).
Предусмотрена пространственно-временная оптимизация управления индукционным нагревателем. При оптимизации управления индукционным нагревателем поставлены задачи быстродействия и на минимум расхода энергии.
При заданных электро- и теплофизических свойствах материала заготовки распределение и мощность внутренних источников теплоты определяются многими факторами, в том числе конструктивными параметрами индуктора, электрической схемой его включения, напряжением на индукторе при постоянном числе витков, частотой тока. Отсюда видна тесная связь задачи управления индукционным нагревателем с задачей его конструирования и проектирования. Поэтому конструирование индуктора можно рассматривать как отдельный этап в решении общей задачи управления [1].
За основу был взят цилиндрический четырехслойный индуктор, питающийся током 50Гц. Частота 50Гц в сравнении со средними и высокими частотами применяется главным образом для низкотемпературного нагрева. Значительно снижаются расход энергии и капитальные затраты в связи с отсутствием преобразователя частоты, уменьшается время нагрева изделия. Например, в установках с питанием от тиристорных преобразователей расход электроэнергии составляет 380-400кВт*ч/т, а при питании нагревателей от сети 50Гц - 360кВт*ч/т расход воды также снижается на 8-10%.
Исследовалось распределение объемной мощности индуктора по длине заготовки при различных конструкциях индуктора (рис.2), изменение заглубления индуктора относительно заготовки несущественно для улучшения процесса нагрева. Результаты исследований представлены на рис.З.
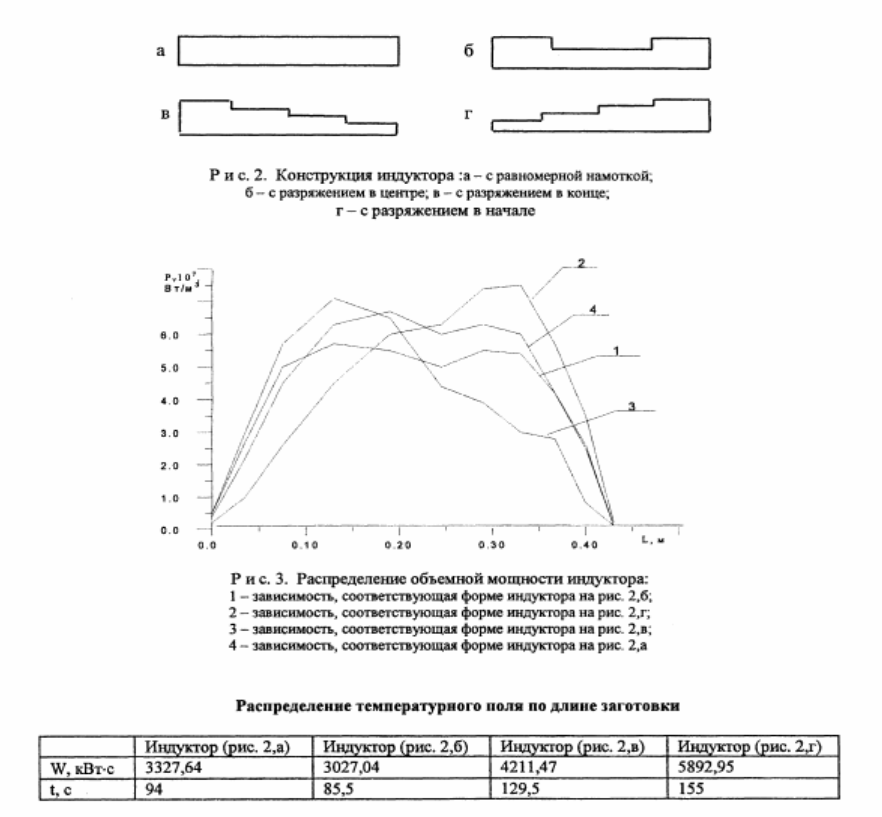
Анализ зависимостей показал что, наилучший вариант распределения температурного поля по длине заготовки (по критериям быстродействия и энергозатрат) получен при форме индуктора (б) на рис. 2,6 (см. таблицу). В данном случае время плавления до температуры 70 °С - 85,5с., энергозатраты - 3027,04кВт-с при токе 1кА. На основе этих моделей была построена замкнутая система регулирования с релейным регулятором. Точка контроля выбиралась на основании исследуемых тепловых полей.
Список использованной литературы
1. Немков В. С., Демидович В. Б. Теория и расчет устройств индукционного нагрева. Д.: Энергоатомиздат, 1979
2. СлухоцкийА. Е. Установки индукционного нагрева. Д.: Энергоиздат, 1981.
3. Зенкевич О., Морган К. Конечные элементы и аппроксимация. М.: Мир, 1986.
4. Норри Л., Ж де Фриз. Введение в метод конечных элементов. М.: Мир, 1981.