Автор:
Бершадский И.А1, Гладков А.Ю2, Згарбул А.В1, Шлепнёв С.В1, Мых А.Д11 Донецкий национальный технический университет,
С целью исключение ложных срабатываний устройства защиты от дугового пробоя (УЗДП) проведен поиск но-вых и рассмотрены комбинации уже существующих методов обработки входящих на микроконтроллер данных, которые могут значительно отличаться от вида подключаемой в сеть нагрузки. В результате исследований разра-ботан новый метод идентификации последовательных дуговых замыканий в электрической сети жилых зданий на основе дискретного вейвлет-преобразования (DWT). Метод включает в себя дискретно-временной анализ на основе моделирования в математическом пакете Matlab экспериментальных кривых тока с дуговыми пробоями, а также извлечение признаков дугового пробоя с использованием метода обработки сигнала, называемого вейвлетами семейства Daubechies db4. Верификация и сравнительный анализ модели обнаружения последовательного дугового пробоя рассмотрен на примере двух типовых нагрузок бытовой электрической сети: обогреватель мощностью 2,2 кВт и пылесос с симисторным регулятором мощности. Установлено, что дуговые пробои имеют уникальные особенности в своих кривых тока, а именно: уровень нормализованных в относительных единицах коэффициентов детализации cd DWT во временной области на частоте дискретизации 10 кГц показывают значения: 1 уровень- от 0,2 до 0,5 и выше, 2 уровень – от 0,05 до 0,2 и выше. Установлено, что уровень нормализованных в относительных единицах коэффициентов детализации DWT во временной области на частоте дискретизации 10 кГц при нормальной работе в каждом масштабе относительно малы – 1 уровень < 0,1 и 2 уровень< 0,04. Это позволит характеризовать интенсивность искрения матрицей SAF, строки которой соответствуют уровню нормализованного cd1, а столбцы – номеру полупериода 1...10.
Дуговой пробой, электрическая сеть, потребитель электроэнергии, вейвлет-преобразование, переходной процесс, сила тока, частота дискретизации, микроконтроллер
В распределительных сетях низкого напряжения существует высокий риск возникновения пожаров, вызванных неисправностями электропроводки.
Отметим, что последние 5 лет в Российской Феде-рации пожары от электроустановок занимают лидиру-ющее место и составляют более 34 % от их общего числа [1]. Около 90 % этого объема приходится на жилой сектор, где основной 1причиной пожаров являются неисправности кабельных изделий, электроустановочных устройств (электрические розетки, вилки, выключатели, разветвители и т.п.) и осветительных приборов.
Одной из распространенных причин пожаров явля-ются дуговые пробои, которые в основном возникают из-за электрических проблем, таких как старение кабе-лей и ослабление контактных соединения. Создавая высокую температуру и распыляя расплавленный ме-талл, дуговые пробои в конечном итоге приводят к пожарам по электротехническим причинам [2].
Обычные защитные устройства, такие как автома-тические выключатели, предохранители или прерыва-тели тока утечки не способны обнаружить эту неис-правность, так как ток дуги остается ниже уровней отключения теплового или мгновенного расцепителей.
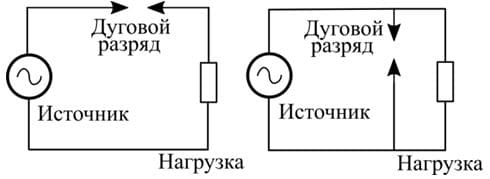
Известны два типа дуговых замыканий: последова-тельные и параллельные. Первый тип, показанный на рис. 1, а, является наиболее распространенным и воз-никает при обрыве одного силового проводника. Максимальный ток дуги ограничивается током нагрузки из-за последовательного соединения и, в зависимости от этого тока может выделяться или не выделяться значительное количество тепла, вызывающего пожароопасное состояние ослабленных контактов.
Рис. 1. Дуговое замыкание: последовательное (а) и параллельное (б)
Параллельное дуговое замыкание, показанное на рис. 1, б, возникает между нейтральным и фазным проводником, когда изоляция повреждена из-за меха-нического, температурного напряжения или старения. В этом случае высокоомная дуга сначала расплавляет и карбонизирует изоляцию, а затем образуется токовый тракт, который может повлечь возгорание.
Устройства защиты от образования дуги (УЗДП) уже существуют и представляют собой микропроцес-сорный модульный релейный аппарат, предназначен-ный для электрической цепи класса до 0,4 кВ. Но экс-перименты показывают, что они часто не устраняют такие неисправности [3]. При проектировании и экс-плуатации УЗДП также остались не решенными пол-ностью проблемы, вызванные ложными срабатывани-ями из-за электромагнитных помех, не связанных с аварийным искрением.
А. Недостатки существующих подходов.
Многие из существующих подходов к обнаруже-нию дуговых замыканий изучают форму сигнала тока и его первую и вторую производные, чтобы идентифи-цировать пики, нулевые “площадки” или быстрое нарастание фронта после нулевой “площадки” [4]. Другим способом распознать возникновение дуги яв-ляется анализ широкополосного высокочастотного шума (ВЧ) в диапазоне от 5 до 50 МГц. Например, в [5] высокочастотный компонент анализируется путем построения срезов трехмерной поверхности на основе биспектра. В других источниках непериодичность сиг-нала рассматривается как критерий обнаружения дуги [6]. Для методов обнаружения ВЧ принятые методы цифровой обработки сигналов приводят к необходимо-сти точного измерения ВЧ-составляющих и, следова-тельно, высокой частоты дискретизации [7], что требу-ет высокозатратных микроконтроллеров и АЦП.
Функция "нулевой паузы" сама по себе не подходит для нелинейных нагрузок в качестве метода обнаруже-ния, и требуется её дальнейшая обработка.
В то же время наиболее перспективным с точки зрения диагностических характеристик можно при-знать развиваемые в последнее время для извлечения признаков неисправности (дугового пробоя) Вейвлет-преобразования [8]. Они позволяют учитывать неста-ционарность токовых сигналов дугового пробоя и адаптировать к сигналу выбор параметров окна по времени.
Можно классифицировать непрерывные вейвлет-преобразования (CWT) и дискретные вейвлет-преобразования (DWT).
Вейвлеты - это математические функции, похожие на синусоидальные волны, с той разницей, что они имеют «конечную колебательную природу». Дискрет-ное вейвлет-преобразование оказалось полезным при анализе переходных процессов, таких как те, которые связаны с дуговыми пробоями в электропроводке жи-лых зданий.
Б. Анализ дискретного вейвлет-преобразования.
Итеративный процесс анализа сигнала в рамках набора фильтров DWT называется анализом с несколь-кими разрешениями (MRA). На первом этапе декомпо-зиции сигнал поступает в фильтр нижних частот (LPF), специфичный для определенной функции масштаби-рования основного вейвлета. Коэффициенты аппрок-симации (са) могут быть получены после свертки вы-борок сигнала с коэффициентами передаточной функ-ции низкочастотного фильтраg и понижающей дискре-тизацией в 2 раза, т.е. исходная длина вектора данных уменьшается вдвое [9].
где gk – параметры НЧ фильтра, k – порядок коэффи-циента фильтра ( и принимает как отрицатель-ные, так и положительные значения), n – номер точки обрабатываемого сигнала, j – уровень вейвлет-преобразования (декомпозиции).
Чтобы получить коэффициенты детализации (сd) сигнала на первом уровень декомпозиции, его необходимо ввести в высокочастотный фильтр h, специфичный для вейвлет-функции, и свернуть его выборки с параметрами передаточной функции фильтра, также затем уменьшив дискретизацию в 2 раза (.рис. 2.).
где hk – параметры ВЧ фильтра.
На втором уровне декомпозиции коэффициенты аппроксимации, полученные на первом этапе, будут обрабатываться таким же образом, как при обработке входного сигнала для получения коэффициентов сa и сd.
Рис. 2. DWT анализ с несколькими масштабными разрешениями (б)
Существование такого набора фильтров зависит от двух типов функций, которые являются функцией масштабирования и вейвлет-функцией, специфичными для определенных типов материнских вейвлетов.
Исключение ложных срабатываний УЗДП достига-ется за счет поиска новых и комбинации уже суще-ствующих методов обработки входящих на микро-контроллер данных, которые могут значительно отли-чаться от вида подключаемой в сеть нагрузки.
В данной работе предложен новый метод обнару-жения последовательного дугового пробоя в электри-ческой сети жилых помещений.
Для применения алгоритма обнаружения неисправ-ностей, первоначально собраны и обобщены данные экспериментальных исследований, которые проводи-лись на платформе (рис. 3) с шагом по времени: 0,004 мкс; 0,2 мкс; 0,01 мс; 0,04 мс; 0,1 мс; 0,4 мс. В даль-нейшем при разработке алгоритма распознавания вы-бирался шаг по времени 0,1 мс с учетом реализации на доступном микроконтроллере STM32F401CU6
Исследуемая нагрузка 7 подключена через штеп-сельное соединение 6 (вилка-розетка) к сети 1 через контактор 2 и резистивный шунт 4.
Формирование переходных процессов с искрения-ми при включении и отключении нагрузки происходит за счет контактов однофазного контактора, управляе-мого кнопкой 3 включения его катушкой. Принуди-тельная генерация искрений при работе нагрузки до-стигается за счет обеспечения дребезга в месте присо-единения неизолированного проводника к зажиму контактора.
Измерение переходных процессов силы тока в нагрузке от времени (рис. 4 и рис 5) обеспечивается за счет резистивного шунта 4 с коэффициентом преобра-зования 1В/1А, подключенного к осциллографу 5.
Данные зависимости нормализовались путем при-ведения к безразмерному виду i(t)/imax.
Для моделирования и обработки сигналов токов дуговых пробоев использовался математический пакет Matlab. Вейвлет-анализ токовых диаграмм нагрузок электросетей офисной и бытовой нагрузки 0,4 кВ вы-полнялся в пакете «WaveletToolbox» Matlab [10].
Рис. 2. Схема экспериментального стенда для получения кривой тока дугового пробоя:1 - сеть 220 В 50 Гц; 2 - контактор однофазный (формирователь дуги); 3 - кнопка включения катушки контактора; 4 - резистивный шунт 1 Ом (для измерения силы тока); 5 - осциллограф запоминающий типа TDS 2022; 6 - розетка и вилка для подключения бытовой нагрузки; 7- бытовая нагрузка (LED лампа, пылесос, дрель).
Рис. 4. Кривая тока пылесоса с симисторным регулятором мощности в нормальном режиме работы (шаг по времени - 0,008 мс).
Рис. 5. Кривая тока пылесоса с симисторным регулятором мощности в режиме последовательного дугового пробоя при ослабленном контакте (шаг по времени - 0, 1 мс)
Дискретно-временной анализ осуществлялся функ-цией wavedec, которая возвращает вектора одномерно-го дискретного многоуровневого вейвлет-преобразования.
Её синтаксис:
где I_d – одномерный сигнал; level_max– макси-мальный уровень преобразования; ‘filter’ – типа вейвлета, например, ‘db4’; [c, l] – выходные вектора разложения.
Для извлечения коэффициентов детализации cd на уровнях levels=1, 2...level_max использована функция detcoef с синтаксисом:
сd при level_max=7 представляет собой структуру в виде {(512x) (261x1) … (14x1) } с векторами cd1, cd2…cd7 на соответствующих номеру вектора уровнях вейвлет-преобразования.
Коэффициенты аппроксимации ca на уровнях levels=1, 2...level_max извлекаются функцией appcoef с синтаксисом:
где j - уровень преобразования.
ca(i) возвращает коэффициенты аппроксимации на уровне преобразования I и представляет собой структуру в виде {(512x) (261x1) … (14x1)} с векторами cа1, cа2…cа7.
Затем, признаки дугового пробоя извлекались с ис-пользованием метода обработки сигнала, называемого вейвлеты семейства Daubechies db4. Алгоритм также включал использование пороговых значений, обнару-жения пиков и отключение реле. Верификация и срав-нительный анализ модели обнаружения последова-тельного дугового пробоя рассмотрен на примере двух типовых нагрузок бытовой электрической сети: обо-греватель мощностью 2,2 кВт (рис. 6 и рис. 7) и пылесос с симисторным регулятором мощности (рис. 8 и рис. 9).
С целью проверки эффективности детектирования и универсальности модели было собрано 50 рядов токовых данных для каждого из указанных типов нагруз-ки. Каждый ряд данных, содержащий 10 нормальных полупериодов работы или 10 полупериодов, содержа-щих искрения с частотой дискретизации 10 кГц, т.е. исходный сигнал содержал 1024 точки.
Результаты испытаний показывают, что при обна-ружении данных о последовательных дуговых пробоях производится анализ алгоритма декомпозиции вейвлетпакетов к текущему сигналу при нормальной работе и в режиме искрений за 1...5 периодов промышленной частоты.
Как видно из рис. 6-9, безразмерные значения де-тальных компонент при нормальной работе в каждом масштабе относительно малы – cd1< 0,1, cd2< 0,04. Разложения вейвлетов db4 более высоких порядков на частоте дискретизации 10 кГц неинформативно из-за малого количества исходных точек сигнала.
Рис. 6. Диаграммы токов (оригинальный сигнал) и коэффициентов детализации DWT (1...4 уровни) во временной области. Нагрузка - обогреватель 2,2 кВт в нормальном состоянии
Рис. 7. Диаграммы токов (оригинальный сигнал) и коэффициентов детализации DWT (1...4 уровни) во временной области. Нагрузка - обогреватель 2,2 кВт при ослабленном контакте
В то же время, безразмерные значения детальных компонент при появлении искрения классифицируются на крактовременные – один период и длительные – более одного периода. В первом случае дуговой пробой не представляет пожарной опасности и может от-слеживаться в алгоритме распознавания по интенсив-ности пересечений заданных уровней детальных ком-понент cd. Во втором случае информация кодируется в виде матрицы SAF:
Рис. 8. Диаграммы токов (оригинальный сигнал) и коэффициентов детализации DWT (1…4 уровни) во временной области. Нагрузка - пылесос с симисторным регулятором мощности 1,8 кВт в нормальном состоянии
Рис. 9. Диаграммы токов (оригинальный сигнал) и коэффициентов детализации DWT (1...4 уровни) во временной области. Нагрузка - пылесос с симисторным регулятором мощности 1,8 кВт при ослабленном контакте
где Kj,k - число пересечений компонент cd1 уровней с номером i =1 (0,2...0,3 о.е.), 2 (0,3...0,4 о.е.), 3 (0,4...0,5 о.е.), 4 (>0,5 о.е.) в течении полупериода промышленной частоты j.
Опасность искрения определяем интегральной ин-тенсивностью колебаний по формуле:
m_3=3,0; m_4=4,0 – коэффициенты .
В зависимости от величины H принимаем решение подаем предупреждающий сигнал, либо отключаем нагрузку, либо не реагируем (защита от ложного срабатывания).
Данная работа посвящена выявлению последова-тельных дуговых замыканий. Представлен новый ме-тод идентификации дуговых пробоев в электрической сети жилых зданий на основе дискретного вейвлет-преобразования (DWT) семейства Daubechies db4.
Установлено, что дуговые пробои имеют уникаль-ные особенности в своих кривых тока, а именно: уровень нормализованных в относительных единицах коэффициентов детализации DWT во временной области на частоте дискретизации 10 кГц показывают значения: 1 уровень - от 0,2 до 0,5 и выше, 2 уровень – от 0,05 до 0,2 и выше.
Интенсивность искрения характеризуется матрицей SAF, строки которой соответствуют уровню нормализованного cd1, а столбцы – номеру полупериода 1...10.
1.Пожары и пожарная безопасность в 2019 году. Статисти-ческий сборник / Под общ. ред. Д.М. Гордиенко. М.: ВНИИПО, 2020. 80 с.
2.Монаков В.К. Разработка устройства защиты от дуговых замыканий // Пожаровзрывобезопасность. 2014. Т. 23, №8. С. 27-31.
3.Защита от дугового замыкания для дома: AFDD или УЗМ 50/УЗИС –URL: https://electrikblog.ru/zashchita-ot-dugovogo-zamykaniya-dlya-doma/ (дата обращения 11.11.2023)
4.A Method for Residential Series Arc Fault Detection and Identification, Electrical Contacts / D. Li, Z. Song, J. Wang, Y., H. Chen, L. Yu, B. Liu // Proceedings of the Annual Holm Conference on Electrical Contacts. IEEE, 2009. Pp. 7-13. doi: 10.1109/HOLM.2009.5284428.
5.Series Arc Fault Detection Algorithm Based on Autoregres-sive Bispectrum Analysis / K. Yang, R. Zhang, S. Chen, F. Zhang, J. Yang, X. Zhang // Algorithms. 2015. No. 8(4). Pp. 929-950. doi: 10.3390/a8040929.
6.Wang S.C., Wu C.J., Wang Y.J. Detection of Arc Fault on Low Voltage Power Circuits in Time and Frequency Domain Approach // International Journal of Circuits, Systems and Signal Processing. 2012. No. 6(5). Pp. 324-331.
7.Arc Faults in Low-Voltage Distribution Networks / M. Rashevskaya, A. Kulikov, M. Tibrayev, A. Gudoghnikov // Proceedings of the 17th Conference on Electrical Machines, Drives and Power Systems (ELMA). IEEE, 2021. Pp. 1-5. doi: 10.1109/ELMA52514.2021.9503046.
8.Дьяконов В.П. Вейвлеты. От теории к практике. М.: СОЛОН-Пресс, 2010. 400 с.
9. Discrete Wavelet Transform optimal parameters estimation for arc fault detection in low-voltage residential power networks / P. Qi, S. Jovanovic, J. Lezama, P. Schweitzer // Electric Power Systems Research. 2017. No. 143. Pp. 130-139. doi: 10.1016/J.EPSR.2016.10.008.
10. MathWorks Help Center. Wavedec — URL: https://www.mathworks.com/help/wavelet/ref/wavedec.html (дата обращения 11.11.2023)
IlyaА. Bershadsky
D. Sc. (Engineering), Associate Professor, Head of the Department "Power Supply of Industrial Enterprises and Cities" of the Federal State Budget Educational Institution of Higher Education «Donetsk national technical university», Donetsk; e-mail:ibersh164@yandex.ru
Aleksandr J. Glаdkov
Ph.D. (Engineering), Head of the Laboratory of Intrinsic Safety of the State Institution "Makeyevsky Research Institute for the Safety of Work in the Mining Industry", Makeyevka; e-mail:gladkov5555@rambler.ru.
Andrej V. Zgarbul
Ph.D. (Engineering), Associate Professorof the Department "Power Supply of Industrial Enterprises and Cities" of the Federal State Budget Educational Institution of Higher Education «Donetsk national technical university», Donetsk; e-mail: zgarbul.andrey@gmail.com
Sergej V. Shlepnjov
Ph.D. (Engineering), Associate Professor, Dean of the Faculty of Intelligent Electric Power Engineering and Robotics of the Federal State Budget Educational Institution of Higher Education «Donetsk national technical university», Donetsk; e-mail: shlepnev71@mail.ru
Anatolij D. Myh
Graduate student of the Department "Power Supply of Industrial Enterprises and Cities" of the Federal State Budget Educational Institution of Higher Education «Donetsk national technical university», Donetsk; e-mail: vip.myh@mail.ru
In order to eliminate false alarms of the arc faultdetection device (AFDD), a search was conducted and combinations of existing methods of processing data entering the microcontroller were considered, which may differ signifi-cantly from the type of load connected to the network. As a result of the research, a new method for identifying se-quential arc circuits in the electrical network of residential buildings based on discrete wavelet transform (DWT) has been developed. The method includes a discrete-time anal-ysis of experimental current curves with arc breakdowns in the mathematical package Matlab, as well as the extraction of signs of arc breakdown using a signal processing method called wavelets of the Daubechiesdb4 family. Verification and comparative analysis of the sequential arc breakdown detection model is considered on the example of two typical household electrical network loads: a 2.2 kW heater and a vacuum cleaner with a triac power regulator
In order to eliminate false alarms of the arc faultdetection device (AFDD), a search was conducted and combinations of existing methods of processing data entering the microcontroller were considered, which may differ signifi-cantly from the type of load connected to the network. As a result of the research, a new method for identifying se-quential arc circuits in the electrical network of residential buildings based on discrete wavelet transform (DWT) has been developed. The method includes a discrete-time anal-ysis of experimental current curves with arc breakdowns in the mathematical package Matlab, as well as the extraction of signs of arc breakdown using a signal processing method called wavelets of the Daubechiesdb4 family. Verification and comparative analysis of the sequential arc breakdown detection model is considered on the example of two typical household electrical network loads: a 2.2 kW heater and a vacuum cleaner with a triac power regulator It is established that arc breakdowns have unique features in their current curves, namely: the level of detail coefficients normalized in relative units of CDDWT in the time domain at a sampling frequency of 10 kHz shows the values: 1 level - from 0.2 to 0.5 and higher, 2 level – from 0.05 to 0.2 and higher. It has been established that the level of detail coefficients normalized in relative units in the time domain at a sampling frequency of 10 kHz at normal operation at each scale relative to the scale is level 1 < 0.1 and level 2< 0.04. This will allow us to characterize the intensity of sparking by the SAF matrix, the rows of which correspond to the level of normalized cd1, and the columns correspond to the half–period number 1..10.
Keywords:Arc fault, electrical network, electric power consumer, wavelet transform, transient, current strength, sampling rate, microcontroller
1. Fires and fire safety in 2019. Statistical collection / edited by. ed. D.M. Gordienko. M.: VNIIPO, 2020. 80 p.(InRussian)
2. Monakov V.K. Development of a protection device against arc faults // Fire and Explosion Safety, 2014, vol. 23, no. 8, p. 27-31 (In Russian)
3. Arc fault protection for home: AFDD or UZM 50/UZIS. [Electronic resource]: https://electrikblog.ru/zashchita-ot-dugovogo-zamykaniya-dlya-doma/ (In Russian)
4. Dongwei Li, Zhengxiang Song, Jianhua Wang, YingsanGeng, Huilin Chen, Li Yu, Bo Liu A. Method for Residential Series Arc Fault Detection and Identification, Electrical Contacts, Proceedings of the Annual Holm Conference on Electrical Contacts, pp. 7-13, October 2009. doi: 10.1109/HOLM.2009.5284428
5. K. Yang, R. Zhang, S. Chen, F. Zhang, J. Yang, X. Zhang: Series Arc Fault Detection Algorithm Based on Autoregres-sive Bispectrum Analysis, Algorithms, Vol. 8, No. 4, Decem-ber 2015, Pp. 929?950. doi: 10.3390/a8040929
6. Sh.- Ch. Wang, Ch.- J. Wu, Y.- J. Wang: Detection of Arc Fault on Low Voltage Power Circuits in Time and Frequency Domain Approach, International Journal of Circuits, Systems and Signal Processing, Vol. 6, No. 5, 2012, Pp. 324-331.
7. M. Rashevskaya, A. Kulikov, M. Tibrayev, A. Gudoghnikov: Arc Faults in Low-Voltage Distribution Networks, Proceed-ings of the 17th Conference on Electrical Machines, Drives and Power Systems (ELMA), Sofia, Bulgaria, July 2021, Pp. 1-5. doi: 10.1109/ELMA52514.2021.9503046
8. Dyakonov V.P. Wavelets. From theory to practice. – M.: SOLON-Press, 2010 – 400 p. (In Russian)
9. Pan Qi, S. Jovanovic, J. Lezama, P. Schweitzer Discrete Wavelet Transform optimal parameters estimation for arc fault detection in low-voltage residential power networks, Electric Power Systems Research, 143, 12p., February 2017. doi: 10.1016/J.EPSR.2016.10.008
10. MathWorks Help Center. wavedec [Электронный ресурс]. — Режим доступа: https://www.mathworks.com/help/wavelet/ref/wavedec.html