Автор: В.В. Гусев, Д.А. Моисеев
Источник: Донецкий национальный технический университет
В статье рассмотрен вопрос оценки состояния рабочей поверхности алмазного шлифовального круга при обработке керамики. Предложено описывать профиль зерен алмазного шлифовального круга с учетом площадок износа на них на основании результатов профилографировании рабочей поверхности круга.Состояние рабочей поверхности круга можно оценить с помощью скалярной характеристики относительной опорной длиной профиля зерен на определенном расстоянии от наружной поверхности.
Ключевые слова:керамика, алмазный круг,рабочая поверхность круга, профилографирование, стереологическая реконструкция поверхности.
V. V. Gusev, D. A. Moiseenco
In article the question of an assessment of a condition of a working surface of a diamond grinding wheel when processing ceramics is considered. It is offered to describe a profile of grains of a diamond grinding wheel taking into account platforms of wear on them on the basis of results of a profilografirovaniya of a working surface of a wheel. The condition of a working surface of a wheel can be estimated by means of the scalar characteristic - the relative basic length of a profile of grains at a certain distance from an external surface.
Keywords:ceramics, diamond wheel,working surface of a wheel, profilografirovaniye, stereological reconstruction of a surface.
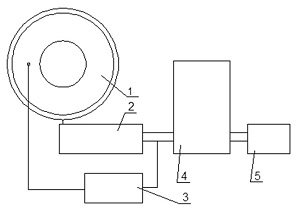
Введение. Профилографирование рабочей поверхности круга (РПК) отличается от других методов исследования простотой и большим объемом получаемой информации, но имеет систематическую погрешность, вызванную тем, что ощупывающий наконечник при своем прямолинейном перемещении не попадает на вершины большинства режущих кромок, а проходит по их боковым сторонам.На кафедре мехатронные системы машиностроительного оборудования ДонНТУ было разработано специальное устройство (рис.1) для записи режущего профиля алмазного круга на металлической связке с выделением зерен из общего рельефа круга [1]. Оно построено на базе профилограф-профилометра 4, электронного блока 3 и приспособления 2. Информация выводится на ленту самопишущего прибора профилограф-профилометра 5.
На приспособлении 2 располагается датчик профилограф-профилометра, который регистрирует колебания коромысла с лопаточкой, которое, перемещающегося в соответствии с изменением профиля круга. Здесь же располагается привод вращения круга, состоящий из малооборотного двигателя, блока редукции и приводного капролонового ролика. При помощи пониженной редукции достигается очень малая частота вращения алмазного круга – 1 оборот за 10 часов для круга диаметром 200 мм, соответствующая линейной скорости перемещения, равной 1 мм/мин. Такая скорость трассировки круга соответствует скоростям протяжки датчика, применяемым при профилографировании поверхности детали.

2. Основное содержание и результаты работы. Перед записью профиля РПК производилась тарировка всего измерительного устройства. Для этого использовалась микрометрическая скоба с ценой деления 2 мкм. Длина профилограммы составляетне менее 15-20 мм рабочей поверхности круга.Привод вращения круга имеет возможность смещения в вертикальном направлении, что позволяет его использовать для различных размеров алмазных кругов. В качестве контактирующего элемента применяется лопаточка, выполненная из закаленной стали. Толщина ее составляет 0,05 мм, а ширина варьировалась в пределах от 0,1 до 0,7 мм в зависимости от зернистости круга и задач исследований. Запись алмазных зерен воспроизводит изображение набора частиц, находящихся в пересекаемой плоскости щупа, в искаженном виде, как это показано на рис.2. Профилограмма поверхности круга является плоскостью ортогональных проекций всех элементов структуры, содержащихся в объеме, отсекаемом краями щупа. Анализ получаемого рельефа круга по профилограмме требует применения методов стереологической реконструкции поверхности, которая аналогична анализу структуры фольги при электронной микроскопии [2].
При профилографировании лопаточкой с выделением связки за счет ее токопроводности происходит то же, что и при исследовании тонкой фольги или тонкого среза поля непрозрачных элементов в прозрачной среде. Две параллельные плоские секущие, лежащие на расстоянии друг от друга, проходят сквозь структуру. Структуру рабочей поверхности круга можно представить как бы состоящей из непрозрачных зерен в прозрачной среде. При этом на профилограмме наблюдаются вертикальные проекции частей зерен, лежащих между плоскостями, проходящими через края щупа (см. рис.2).
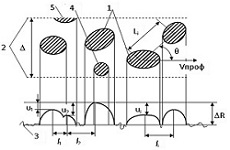
Плоскость наблюдения воспроизводит изображение набора зерен, находящихся в пересекаемой плоскости в искаженном виде. Большие зерна закрывают меньшие и их изображения могут перекрываться. Число изображений на проекции NА не будет равно истинному числу зерен вследствие эффекта экранирования и присутствия сечений тех зерен, которые пересекаются краями щупа. Эффект экранирования проявляется при д/ dз>1, где dз– средний диаметр зерна. Так как при 100% концентрации алмазов объем, занимаемый ими, составляет 0,25, то для определения истинного числа зерен используем метод Хиллиарда [2]. Определение числа зерен в единице объема NV не требует поправок на экранировку и пересечение и заключается в экстраполяции NА(д) к нулевой толщине слоя (лопатки). Определяют NAи H (средняя ширина зерен) для нескольких толщин лопаточки и строят график в координатах ln (HА+д*H) - д и на оси координат при д=0 находят lnNa
Проекционное изображение элементов структуры круга при профилографировании (см. рис. 2) требует, как и в случае определения истинного числа зерен на поверхности по измерению расстояния между вершинами зерен lз на профилограмме, определить ее истинное значение Lз. Для случая, когда вершины зерен в зоне профилографировании и направление между двумя ближайшими вершинами (задаваемое углом ) распределены равновероятно, можно воспользоваться при определении истинного расстояния между вершинами зерен зависимостью Lз=4*Iз/п, предложенной в работе [3]. При этом ширина лопаточки д при профилографировании должна находиться в пределах dз<=д<=2dз, где dз– средний диаметр алмазных зерен. В противном случае происходит экранирование одних зерен другими и искажение в определении истинного расстояния между вершинами зерен.
При изучении формы поперечного среза наиболее часто [4] используют универсальное выражение, описывающее изменение ширины зерна (bз) от его высоты
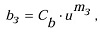
где Сb и mз - эмперические коэффициенты, u - координата, отсчитываемая от вершины алмазного зерна
Были проведены исследования профиля зеренкруга 1А1 250х20х76 АС6 125/100 – 4 – М2-01после правки электроэрозионным методом и удаления 22 см3ситалла на единицу ширины круга.После обсчета записанного профиля зернаосуществлялся переход от эквидистанты к реальному профилюс учетом радиуса закругления щупа.При экспериментах использовался щуп шириной 0,1 и 0.5 мм.Результаты обработки профилограмм зерен (на глубину до10мкм) показали, что показатель степени m имел значение 0,50,02 независимо от состояния круга и ширины щупа.Коэффициент Сb принимал значенияот 8 до 16.При коэффициентеСb=14 значение ширина зерна совпадает с размерами эллипса, описывающего зерно средних размеров для принятой зернистости и ориентированного вдоль большей его полуоси (bэ=53,8) [5].При Сb=8 результаты совпадают с экспериментальными значениями (в случае моделирования зерна конусом с шаровым сегментом у вершины)Лукина Л.Н. [6].
При работе шлифовального круга на поверхности алмазных зерен образуется площадка износа рис.3. В связи наличием у профиля зерна площадки износа при вершине шириной , действительный профиль зерна следует аппроксимировать системой из 2 уравнений:
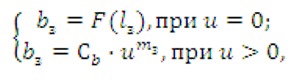
где F(lз) - функция распределения длин площадок износа на зерне.
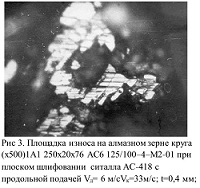
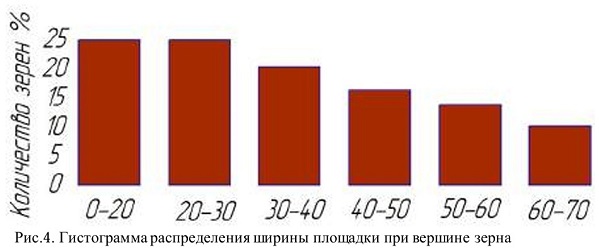
Количество зерен с такой площадкой износа на зерне составляет до 70% от общего числа зерен. Как показал профилограмм, ширина площадки является анализ этой величиной переменной и изменяется от 5 до 70 мкм для исследуемой зернистости круга. Распределение площадок износа по размерам приведено на рис.4. Статистическая обработка распределения длин площадок износа показала, что распределение длин площадок износа на алмазных зернах адекватно(в соответствии с критерием 2) описывается одним из следующих законов: Вейбулла, экспоненциальным или гамма распределениями.Доля зерен с б) площадка износа х500раз площадками износа у наружной поверхности РПК возрастает. После правки на рабочей поверхности круга остаются зерна с площадкой износа, однако их количество сокращается.
Распределение на рабочей поверхности круга вершин зерен по высоте u является неравномерным. Исходное состояние разновысотности вершин алмазных зерен круга после правки и ее изменение при обработке хрупких неметаллических материалов в соответствии с экспериментальными результатами адекватно описывается распределением Вейбулла [7] с плотностью
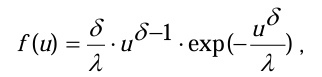
где дельта и гамма - параметры распределения (дельта>0, гамма>0), определялись экспериментально по результатам профилографирования круга непосредственно на станке.
Пусть вершина зерна находится на расстоянии u от наружной поверхности круга. В этом случае в сечении рабочей поверхности круга на расстоянии с (с>u) от наружной поверхности круга площадь зерна Sзпоп(u) определяется как
![]()
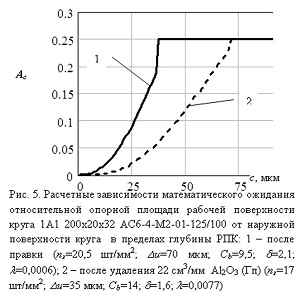
Используя полученную зависимость 5, можно определить математическое ожидание относительной опорной площади рабочей поверхности круга РПК для любого расстояния от наружной поверхности круга в пределах глубины РПК (0<=с=<дu ). На рисунке 5 показано изменение РПК круга 1А1 250х20х32 АС6 125/100 -4М2-01-после правки (дu=70мкм) и после съема 22 см3 керамики Аl2O3 (Гп) (дu=35мкм).В обоих случаях относительная опорная площадь рабочей поверхности изменяется от 0 до 0,23 и от 0 до 0,19 у связки соответственно после правки длительной и после работы. Полученные значения несколько превышают величину относительной опорной площади профиля tp=0,25 дu/dз, предложенную в работе [8] для расчета числа алмазных зерен на поверхности круга при концентрации алмазов 100%. Разница в результатах расчета существенно для круга, длительное время находившегося в работе, что связано, по всей видимости, со способностью удержания связкой частично разрушенных и изношенных алмазных зерен.В соответствии с одним из фундаментальных соотношений стереологии (принципом Кавальери-Акера-Глаголева) отношение суммарной площади плоских площадок – сечений алмазных зерен к общей площади секущих плоскостей Ас(c) (относительная опорная поверхность) будет равно отношению суммарного объема алмазных частиц к объему образца, т.е. объемной доле алмазных зерен (V(c)).Объемная концентрация алмазов (при 100%) в круге составляет 0,25. Величина относительной опорной площади алмазных зерен у связки не может превышать указанного значения. Объем, занимаемый зернами на рабочей поверхности круга, возрастает от минимального значения у наружной поверхности к значению немногим меньшим объемной концентрации зерен в связке. Случайное поле алмазных зерен на РПК обладает свойствами однородности и изотропности, т.е. профили любых нормальных сечений РПК имеют одинаковые статистические характеристики.Для оценки рабочей части профиля используют математическое ожидание числа зерен на единице длины круга и математическое ожидание относительной опорной длины профиля зерен на произвольном уровне (с). В соответствии с принципом Кавальери Акера-Глаголева отношение суммарной длины отрезков, отсекаемых зернами, к общей длине базовой линии L(c) равно L(c)=Aс(c). Таким образом, скалярная характеристика поля ШК характеризует и вероятностную суммарную ширину зерен на данном уровне c.
Заключение. Таким образом, выполненные экспериментальные исследования зерен на РПК показали, что при описании профиля зерен необходимо учитывать наличие площадок износа на них. Распределение вершин зерен на рабочей поверхности круга можно рассматривать как нестационарное поле с распределением Пуассона. Каждому уровню рабочей поверхности круга соответствует определенная скалярная величина, которая характеризует относительную опорную площадь поверхности алмазных зерен, объемную долю алмазных зерен и определяет возможность в удалении материала припуска инструментом на этом уровне. В процессе работы круга происходят изменения на его рабочей поверхности, связанные с износом алмазных зерен, которые необходимо учитывать при описании скалярной характеристики круга -математическое ожидание относительной опорной длины профиля зерен на определенном расстоянии от наружной поверхности.