Реферат по теме выпускной работы
Содержание
- Введение
- 1. Решение проблемы обнаружения неисправных чипов с помощью машинного обучения
- 1.1 Проблема обнаружения неисправных чипов
- 1.2 Использование машинного обучения для обнаружения неисправных чипов
- 2. Сравнительный анализ алгоритмов для обнаружения неисправных чипов
- 2.1 Сверточная нейронная сеть
- 2.2 Алгоритм k-ближайших соседей (K-Nearest Neighbors)
- 2.3 Метод опорных векторов (Support Vector Machines)
- 2.4 Логистическая регрессия
- Выводы
- Список источников
Введение
Каждая печатная плата должна проходить определенное тестирование до и после того, как она сойдет с конвейера. Цели тестирования разнообразны, и существует огромное количество тестов, которые можно выполнить для любой печатной платы. Конкретные тесты, необходимые для конкретной печатной платы, зависят от приложения и среды, в которой плата будет работать. Из всех тестов, которые можно выполнить для PCBA, тестирование компонентов, пожалуй, является наиболее важным [1].
Производители микросхем используют больше различных традиционных типов инструментов, чем когда-либо, для поиска серьезных дефектов в современных микросхемах, но они также обращаются к дополнительным решениям, таким как передовые формы машинного обучения, чтобы помочь решить проблему.
Сегодня машинное обучение используется некоторыми, но не всеми производителями микросхем. Некоторые используют его на различных этапах технологического процесса. Это зависит от компании.
На заводе-изготовителе некоторые системы метрологии и контроля используют машинное обучение для поиска дефектов. Предположительно, машинное обучение автоматизирует процесс, но это не всегда работает таким образом. Иногда система требует ручного вмешательства оператора для извлечения и проверки данных.
В рамках данного реферата необходимо сделать обзор и анализ аналогов алгоритмов машинного обучения, которые могут использоваться для обнаружения неисправных чипов.
1. Решение проблемы обнаружения неисправных чипов с помощью машинного обучения
1.1 Проблема обнаружения неисправных чипов
Производители компонентов прилагают большие усилия для выявления и удаления неисправных компонентов со своих складов до того, как они поступят в цепочку поставок, но иногда некачественная партия попадает в продажу [2]. Важно понимать, как идентифицировать неисправные электронные компоненты, а также как отличить их от неисправности на уровне платы.
Неисправные электронные компоненты можно идентифицировать в три этапа в ходе проекта:
- Перед изготовлением;
- Во время сборки;
- Во время функционального тестирования после получения PCBA.
Производители знают, как идентифицировать неисправные электронные компоненты с помощью набора стандартных тестов. Однако, в то время как полупроводниковые компании делают все возможное для удаления неисправных компонентов из производственных партий, а производители помогают устранять преждевременные сбои с помощью тестирования, идентификация неисправных компонентов в значительной степени зависит от инженеров-испытателей или проектировщиков. После получения платы должны пройти квалификационное тестирование для выявления любых вышедших из строя плат. Затем эти вышедшие из строя платы исследуются на наличие любых возможных вышедших из строя компонентов.
Современные 300-миллиметровые фабрики представляют собой автоматизированные установки, которые поэтапно обрабатывают пластины с использованием различного оборудования. Усовершенствованный логический процесс может включать от 600 до 1000 этапов и более. На разных этапах микросхема проходит различные этапы метрологии и контроля.
Эти шаги имеют решающее значение. Пропущенный дефект может повлиять на производительность на фабрике или выйти за пределы поля и вызвать сбой позже.
При 28 нм и выше метрология и контроль просты. Например, логический транзистор представляет собой плоскость с крупными характеристиками. Производители микросхем могут относительно легко измерять и инспектировать устройства. Это сложнее с полевыми транзисторами FinFET с длиной волны 16/14 нм. Но по мере того, как конструкции микросхем переходят на 10 нм / 7 нм и выше, структуры становятся меньше, и их труднее измерить. То же самое верно для новейших DRAM и устройств NAND.
Как транзисторы, так и устройства памяти по своей природе похожи на 3D. Итак, в случае метрологии инструменты должны получать не только 2D-измерения в конструкциях, но и получать их в трех измерениях экономически эффективным способом.
Проблемы усугубляются тем, что ни один тип инструмента метрологии и контроля не может обнаружить все дефекты. Например, для определения характеристик транзисторов FinFET на заводе требуется более десятка типов инструментов метрологии.
В идеале производителям микросхем нужны инструменты с лучшей чувствительностью и более высокой производительностью при меньших затратах.
В дальнейшем поставщики оборудования для метрологии и контроля будут продолжать совершенствовать свои системы. Между тем, параллельно поставщики оборудования для метрологии / контроля продолжают разрабатывать методы машинного обучения с использованием нейронных сетей. В нейронных сетях система обрабатывает данные и выявляет закономерности. Она сопоставляет определенные закономерности и узнает, какие из этих атрибутов важны.
1.2 Использование машинного обучения для обнаружения неисправных чипов
Подмножество искусственного интеллекта (ИИ), машинного обучения, десятилетиями использовалось в вычислительной технике и других областях. Фактически, ранние формы машинного обучения использовались в метрологии и контроле на фабриках с 1990-х годов для точного определения дефектов в микросхемах и даже прогнозирования проблем с использованием методов сопоставления с образцом [3]. Машинное обучение – это не инструмент или тип оборудования как таковой, а скорее набор программных алгоритмов, используемых системой для помощи в поиске дефектов. Сейчас индустрия либо изучает, либо начинает использовать системы с более совершенными алгоритмами машинного обучения, основанными на больших наборах данных. Это, в свою очередь, предположительно ускоряет циклы обучения.
Это не заменит традиционные методы, по крайней мере, в краткосрочной перспективе. Пока более продвинутые формы машинного обучения не получили широкого распространения на заводах, и некоторые пробелы остаются. Но отрасль добивается прогресса, поскольку стремится решить сложные задачи в области обнаружения дефектов.
На современных фабриках производители микросхем используют различные системы контроля и метрологии для поиска дефектов в микросхемах. Инспекция – это наука о поиске дефектов, в то время как метрология – это искусство измерения структур. Обе технологии используются для обнаружения проблем в устройствах и помогают обеспечить производительность на производстве.
Тем не менее, в каждом узле устройства и структуры становятся меньше. В некоторых случаях размеры структур значительно ниже 1 ангстрема, что равно 0,1 нм. Найти дефекты в таком масштабе гораздо сложнее и дороже.
Для этой цели существуют инструменты, и многие из них включают определенный уровень машинного обучения. До сих пор более продвинутые формы машинного обучения использовались неравномерно. Но по мере разработки передовых алгоритмов машинного обучения для обнаружения дефектов ситуация может измениться. Вопрос в том, имеется ли достаточно достоверных данных, которые позволили бы производителям и производителям упаковки быстро и точно обнаруживать дефекты. Если наборы данных неадекватны, система может выдавать сомнительные или даже неточные результаты.
В любом случае обнаружение дефектов с помощью машинного обучения будет по-прежнему использоваться для некоторых приложений на заводе. Однако по мере развития технологии – это может найти более широкое применение в отрасли.
Но более серьезная проблема заключается в том, что инструмент от одного поставщика включает в себя проприетарное программное обеспечение и не может взаимодействовать с системами других компаний. Некоторые компании работают над интеграцией своих систем для создания сквозного потока обратной связи, но, по словам экспертов, технология все еще находится в стадии исследований и разработок.
В конечном итоге производителям микросхем хотелось бы иметь комплексное интеллектуальное решение для обратной связи с инструментами разных производителей. Некоторые разрабатывают технологию, хотя это требует инвестиций и ресурсов.
2. Сравнительный анализ алгоритмов для обнаружения неисправных чипов
2.1 Сверточная нейронная сеть
CNN – это современные алгоритмы для задач визуального распознавания, состоящие из нескольких этапов обучаемых фильтров, которые свертывают входные данные (изображение, аудио или видео), за которыми следует многослойная сеть восприятия (MLP), как показано на рисунке 2.1. Уровень свертки свертывает входное изображение с помощью набора адаптивных фильтров, чтобы выявить карту объектов, которая состоит из абстрагирования нескольких объектов из входных данных. Многие уровни свертки и объединения накладываются друг на друга, выявляя функции более высокого уровня из более глубоких слоев [4]. Функции, выявляемые на выходе Сети, состоящей из полностью связанных нейронных слоев. Эти уровни реализуют задачу классификации или распознавания с использованием признаков, выделенных слоями свертки. CNN широко используются в приложениях классификации на основе изображений в медицине, при инспектировании инфраструктуры, а также для обнаружения и анализа дефектов поверхности. Известные архитектуры CNN включают Alexnet, GoogLeNet, ResNet и DenseNet.
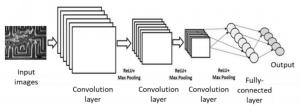
Рисунок 2.1 – Архитектура CNN для классификации изображений
2.2 Алгоритм k-ближайших соседей (K-Nearest Neighbors)
Метод k-ближайших соседей (k Nearest Neighbors, или kNN) – популярный алгоритм классификации, который используется в разных типах задач машинного обучения. Модель kNN представлена всем набором тренировочных данных. Метод k-ближайших соседей представлен на рисунке 2.2.
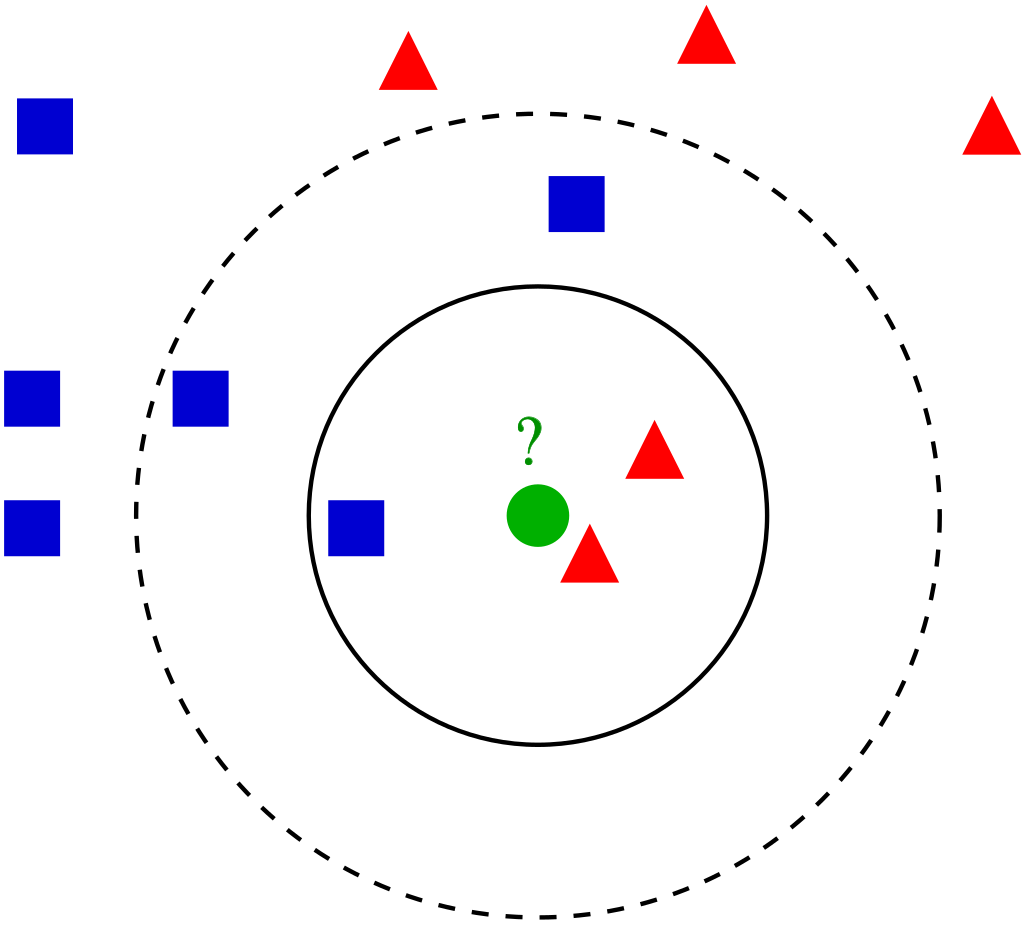
Рисунок 2.3 – Метод k-ближайших соседей
В случае использования метода для классификации объект присваивается тому классу, который является наиболее распространённым среди k соседей данного элемента, классы которых уже известны [5].
Основные шаги для построения данного алгоритма на примере рисунка 2.2:
- У нас есть тестовый образец в виде зеленого круга. Синие квадраты мы обозначим как класс 1, красные треугольники – класс 2.
- Зеленый круг должен быть классифицирован как класс 1 или класс 2. Если рассматриваемая нами область является малым кругом, то объект классифицируется как 2-й класс, потому что внутри данного круга 2 треугольника и только 1 квадрат.
- Если мы рассматриваем большой круг (с пунктиром), то круг будет классифицирован как 1-й класс, так как внутри круга 3 квадрата в противовес 2 треугольникам.
Хотя это может быть не очевидно с самого начала, изменение значения К в данном алгоритме изменит категорию, в которую попадет новая точка данных.
Конкретнее, слишком маленькое значение К приведет к тому, что модель будет точно прогнозировать на обучающем множестве данных, но будет крайне не эффективна для тестовых данных. Также, имея слишком высокий К показатель, вы сделаете модель неоправданно сложной.
Представленный рисунок 3.3 отлично показывает этот эффект.
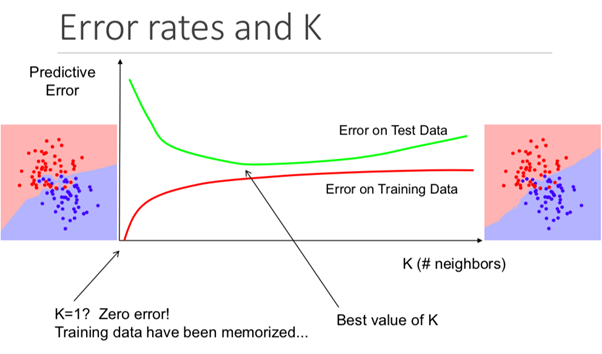
Рисунок 2.3 – Важность переменной К в алгоритме К-ближайших соседей
2.3 Метод опорных векторов (Support Vector Machines)
Метод опорных векторов – это алгоритм классификации (хотя, технически говоря, они также могут быть использованы для решения регрессионных задач), который делит множество данных на категории в местах наибольших «разрывов» между категориями [6]. Эта концепция станет более понятной, если разобрать следующий пример.
Метод опорных векторов (МОВ) – это модель МО с учителем, с соответствующими алгоритмами обучения, которые анализируют данные и распознают закономерности. МОВ может быть использован как для задач классификации, так и для регрессионного анализа.
Метод опорных векторов, вероятно, один из наиболее популярных и обсуждаемых алгоритмов машинного обучения.
Гиперплоскость – это линия, разделяющая пространство входных переменных. В методе опорных векторов гиперплоскость выбирается так, чтобы наилучшим образом разделять точки в плоскости входных переменных по их классу: 0 или 1. В двумерной плоскости это можно представить, как линию, которая полностью разделяет точки всех классов, представлена на рисунке 2.4. Во время обучения алгоритм ищет коэффициенты, которые помогают лучше разделять классы гиперплоскостью.
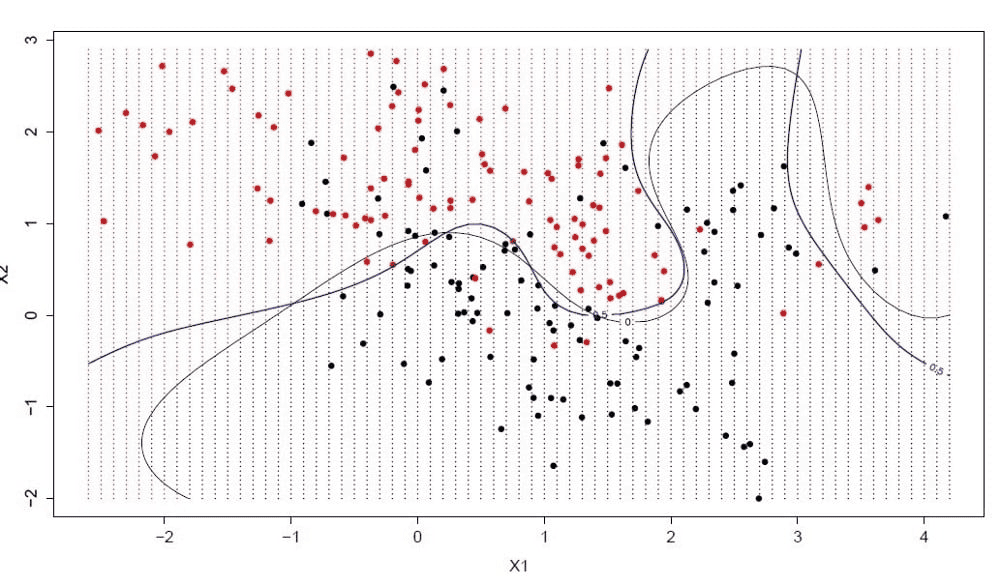
Рисунок 2.4 – Метод опорных векторов
Расстояние между гиперплоскостью и ближайшими точками данных называется разницей. Лучшая или оптимальная гиперплоскость, разделяющая два класса, – это линия с наибольшей разницей. Только эти точки имеют значение при определении гиперплоскости и при построении классификатора. Эти точки называются опорными векторами. Для определения значений коэффициентов, максимизирующих разницу, используются специальные алгоритмы оптимизации.
Метод опорных векторов, наверное, один из самых эффективных классических классификаторов, на который определённо стоит обратить внимание.
2.4 Логистическая регрессия
Логистическая регрессия – это подходящий регрессионный анализ, который следует проводить, когда зависимая переменная является дихотомической (бинарной). Как и любой регрессионный анализ, логистическая регрессия является прогностическим анализом [7]. Логистическая регрессия используется для описания данных и объяснения взаимосвязи между одной зависимой двоичной переменной и одной или несколькими номинальными, порядковыми, интервальными или независимыми переменными на уровне отношений.
Логистическая регрессия похожа на линейную тем, что в ней тоже требуется найти значения коэффициентов для входных переменных. Разница заключается в том, что выходное значение преобразуется с помощью нелинейной или логистической функции.
Несколько примеров классификационных задач МО [8]:
- Спам электронной почты (спам или не спам?);
- Претензия по страховке автомобиля (выплата компенсации или починка?);
- Диагностика болезней.
Каждая из этих задач имеет четко 2 категории, что делает их примерами задач двоичной классификации.
Логистическая функция представлена на рисунке 2.5, и выглядит как большая буква S и преобразовывает любое значение в число в пределах от 0 до 1. Это весьма полезно, так как мы можем применить правило к выходу логистической функции для привязки к 0 и 1 (например, если результат функции меньше 0.5, то на выходе получаем 1) и предсказания класса.
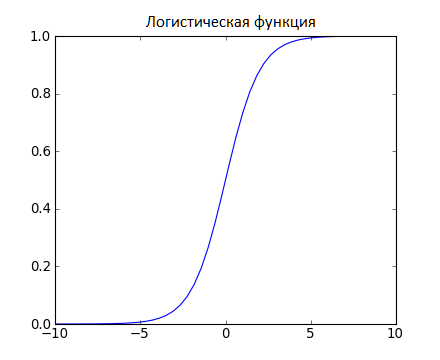
Рисунок 2.5 – Логистическая функция
Причина, по которой логистическая регрессия имеет изгиб – это тот факт, что для её вычисления не используется линейное уравнение. Вместо него логистическая регрессионная модель строится на использовании сигмоиды (2.1) (также называемой логистической функцией, т.к. она используется в логистической регрессии) [9].
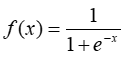
Главная характеристика сигмоиды – не важно какое значение вы передадите этой функции, она всегда вернет значение в промежутке 0-1.
Благодаря тому, как обучается модель, предсказания логистической регрессии можно использовать для отображения вероятности принадлежности образца к классу 0 или 1. Это полезно в тех случаях, когда нужно иметь больше обоснований для прогнозирования.
Как и в случае с линейной регрессией, логистическая регрессия выполняет свою задачу лучше, если убрать лишние и похожие переменные. Модель логистической регрессии быстро обучается и хорошо подходит для задач бинарной классификации.
Выводы
Как можно наблюдать у каждого алгоритма машинного обучения для обнаружения неисправных чипов есть как достоинства, так и недостатки.
Достоинства логистической регрессии [10]:
- логистическая регрессия проста в реализации и легче интерпретировать выходные коэффициенты;
- он не только позволяет оценить, насколько подходящим является предиктор (величина коэффициента), но и направление его связи (положительное или отрицательное).
- логистическая регрессия менее склонна к чрезмерной подгонке, но она может привести к чрезмерной подгонке в наборах данных с высокой размерностью. Можно рассмотреть методы регуляризации (L1 и L2), чтобы избежать чрезмерной подгонки в этих сценариях.
В рамках данного реферата было выполнено:
- описание проблемы обнаружения неисправных чипов;
- описание решения проблемы обнаружения неисправных чипов;
- проведение обзора алгоритмов, которые могут использоваться для обнаружения неисправных чипов.
Полученные результаты планируется использовать в процессе последующей работы над квалификационной работой магистра.
Список источников
- Вьюгин, В.В. Математические основы теории машинного обучения и прогнозирования / В.В. Вьюгин – М.: МОСКВА, 2013. – 387 с.
- Морозова, В. И. Прогнозирование методом машинного обучения / В. И. Морозова, Д. И. Логунова. – М.: Молодой ученый, 2022. – 416 с.
- Агравал, А. Искусственный интеллект на службе бизнеса. Как машинное прогнозирование помогает принимать решения / А. Агравал – М.: «Манн, Иванов и Фербер», 2019. - 336c.
- Искусственный интеллект и машинное обучение, [Электронный ресурс], – Режим доступа: https://azure.microsoft.com/ru-ru/overview/artificial-intelligence-ai-vs-machine-learning/#introduction/
- Айвазян, С. А. Прикладная статистика: классификация и снижение размерности / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин – М.: Финансы и статистика, 1989. – 248 с.
- Метод k-ближайших соседей (k-nearest neighbour), [Электронный ресурс], – Режим доступа: https://proglib.io/p/metod-k-blizhayshih-sosedey-k-nearest-neighbour-2021-07-19
- Bartlett, P. Generalization performance of support vector machines and other pattern classifiers / P. Bartlett, J. Shawe-Taylor – Cambridge: MIT Press USA, 1998. – 189 с.
- Дианов В.Н. Бесконтактный контроль и диагностика соединителей высокопроизводительных вычислительных систем // Вопросы радиоэлектроники. Серия ЭВТ. – 2022. – Вып. 6. – 9 с.
- Саркисов А.А., Власов Д.В., Дианов В. Н. Интеллектуальная диагностика сбоев автомобильных датчиков // Электроника и электрооборудование транспорта. – 2024. – № 3–4. – С. 46–52.
- Бодин А. Б. Моделирование явлений сбоя в соединителях высокопроизводительных вычислительных систем // Электронное моделирование. – 2023. – № 1. – C. 6.
