Аннотация
Чернобай Д.С., Перинская Е.В. Обзор и сравнение алгоритмов для определения неисправных чиповОписана проблема обнаружения неисправных чипов. Описано решение проблемы обнаружения неисправных чипов. Проведён обзор алгоритмов, которые могут использоваться для обнаружения неисправных чипов. Представлен алгоритм логистической регрессии, как инструмент для обнаружения неисправных чипов.
Введение
Каждая печатная плата должна проходить определенное тестирование до и после того, как она сойдет с конвейера. Цели тестирования разнообразны, и существует огромное количество тестов, которые можно выполнить для любой печатной платы. Конкретные тесты, необходимые для конкретной печатной платы, зависят от приложения и среды, в которой плата будет работать. Из всех тестов, которые можно выполнить для PCBA, тестирование компонентов, пожалуй, является наиболее важным [1].
Сегодня машинное обучение используется некоторыми, но не всеми производителями микросхем. Некоторые используют его на различных этапах технологического процесса. Это зависит от компании.
На заводе-изготовителе некоторые системы метрологии и контроля используют машинное обучение для поиска дефектов [2]. Предположительно, машинное обучение автоматизирует процесс, но это не всегда работает таким образом. Иногда система требует ручного вмешательства оператора для извлечения и проверки данных.
В рамках статьи произведём обзор и анализ аналогов алгоритмов машинного обучения, которые могут использоваться для обнаружения неисправных чипов.
Алгоритм k-ближайших соседей (k-Nearest Neighbors)
Метод k-ближайших соседей (k Nearest Neighbors, или kNN) – популярный алгоритм классификации, который используется в разных типах задач машинного обучения. Модель kNN представлена всем набором тренировочных данных. Метод k-ближайших соседей представлен на рисунке 1.
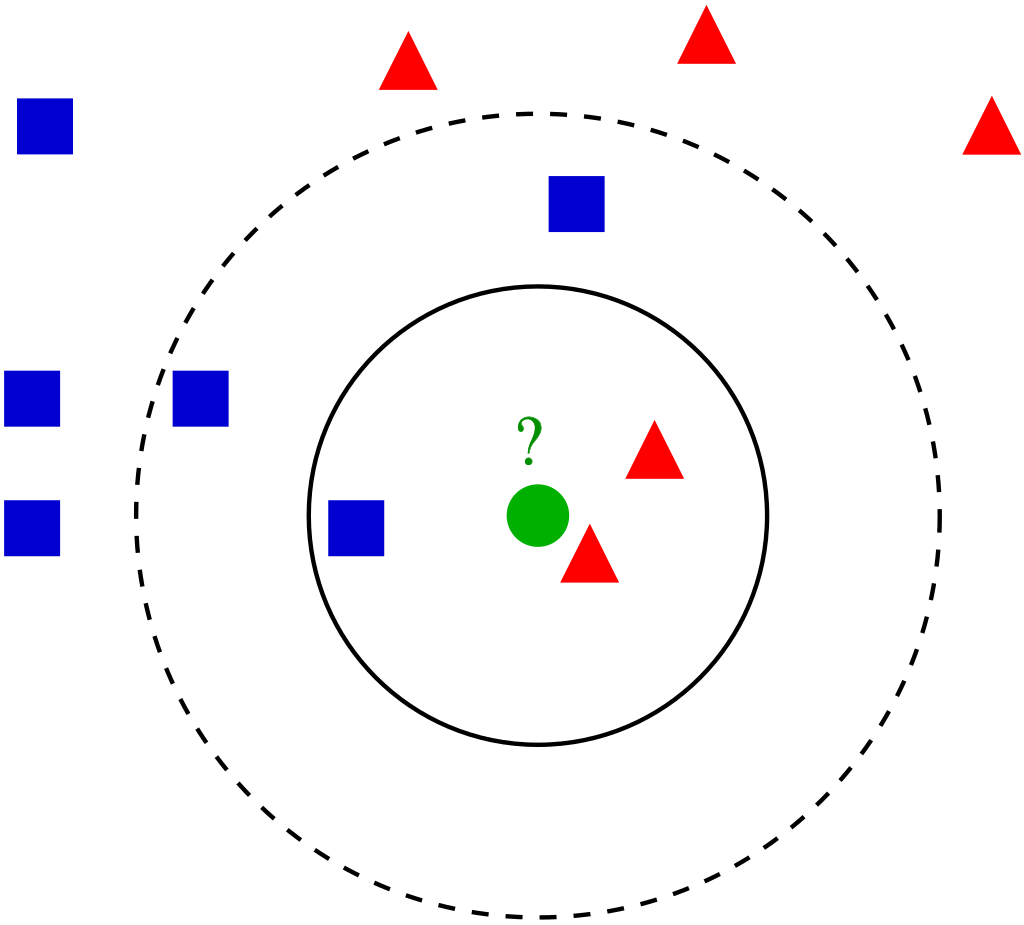
Рисунок 1 – Метод k-ближайших соседей
В случае использования метода для классификации объект присваивается тому классу, который является наиболее распространённым среди k соседей данного элемента, классы которых уже известны.
В случае использования метода для регрессии, объекту присваивается среднее значение по k ближайшим к нему объектам, значения которых уже известны [3].
Основные шаги для построения данного алгоритма на примере рисунка 2:
- У нас есть тестовый образец в виде зеленого круга. Синие квадраты мы обозначим как класс 1, красные треугольники – класс 2.
- Зеленый круг должен быть классифицирован как класс 1 или класс 2. Если рассматриваемая нами область является малым кругом, то объект классифицируется как 2-й класс, потому что внутри данного круга 2 треугольника и только 1 квадрат.
- Если мы рассматриваем большой круг (с пунктиром), то круг будет классифицирован как 1-й класс, так как внутри круга 3 квадрата в противовес 2 треугольникам.
Метод опорных векторов (Support Vector Machines)
Метод опорных векторов – это алгоритм классификации (хотя, технически говоря, они также могут быть использованы для решения регрессионных задач), который делит множество данных на категории в местах наибольших «разрывов» между категориями [4]. Эта концепция станет более понятной, если разобрать следующий пример.
Метод опорных векторов (МОВ) – это модель МО с учителем, с соответствующими алгоритмами обучения, которые анализируют данные и распознают закономерности. МОВ может быть использован как для задач классификации, так и для регрессионного анализа.
Метод опорных векторов, вероятно, один из наиболее популярных и обсуждаемых алгоритмов машинного обучения.
Гиперплоскость – это линия, разделяющая пространство входных переменных. В методе опорных векторов гиперплоскость выбирается так, чтобы наилучшим образом разделять точки в плоскости входных переменных по их классу: 0 или 1. В двумерной плоскости это можно представить, как линию, которая полностью разделяет точки всех классов, представлена на рисунке 2. Во время обучения алгоритм ищет коэффициенты, которые помогают лучше разделять классы гиперплоскостью.
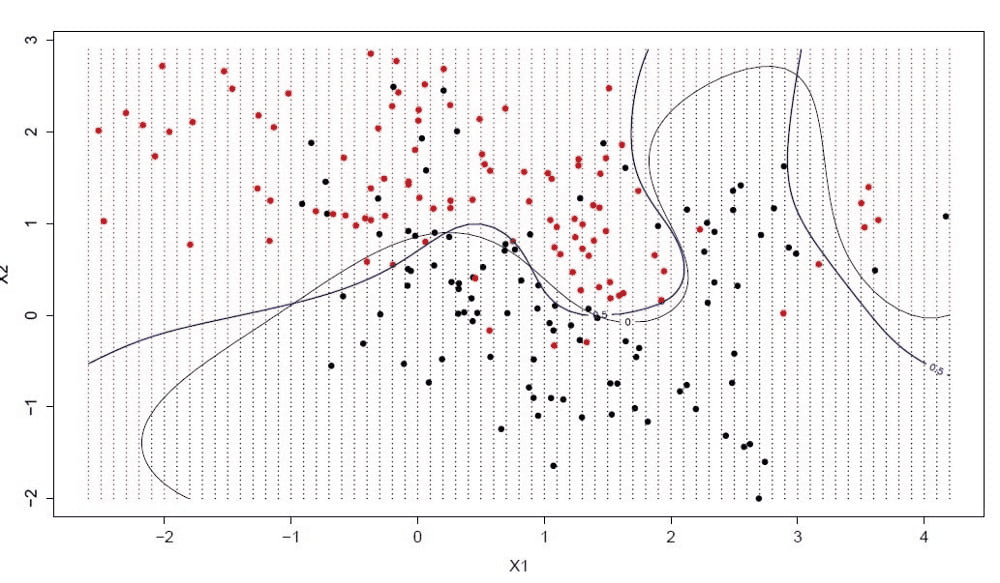
Рисунок 2 – Метод опорных векторов
Расстояние между гиперплоскостью и ближайшими точками данных называется разницей. Лучшая или оптимальная гиперплоскость, разделяющая два класса, – это линия с наибольшей разницей. Только эти точки имеют значение при определении гиперплоскости и при построении классификатора. Эти точки называются опорными векторами. Для определения значений коэффициентов, максимизирующих разницу, используются специальные алгоритмы оптимизации.
Метод опорных векторов, наверное, один из самых эффективных классических классификаторов, на который определённо стоит обратить внимание.
Логистическая регрессия
Логистическая регрессия – это подходящий регрессионный анализ, который следует проводить, когда зависимая переменная является дихотомической (бинарной). Как и любой регрессионный анализ, логистическая регрессия является прогностическим анализом [5]. Логистическая регрессия используется для описания данных и объяснения взаимосвязи между одной зависимой двоичной переменной и одной или несколькими номинальными, порядковыми, интервальными или независимыми переменными на уровне отношений.
Логистическая функция представлена на рисунке 3, и выглядит как большая буква S и преобразовывает любое значение в число в пределах от 0 до 1. Это весьма полезно, так как мы можем применить правило к выходу логистической функции для привязки к 0 и 1 (например, если результат функции меньше 0.5, то на выходе получаем 1) и предсказания класса.
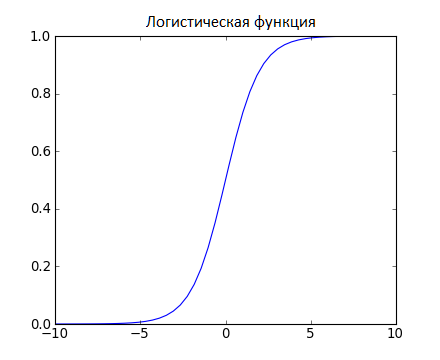
Рисунок 3 – Логистическая функция
Причина, по которой логистическая регрессия имеет изгиб – это тот факт, что для её вычисления не используется линейное уравнение. Вместо него логистическая регрессионная модель строится на использовании сигмоиды (1) (также называемой логистической функцией, т.к. она используется в логистической регрессии).
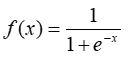
Главная характеристика сигмоиды – не важно какое значение вы передадите этой функции, она всегда вернет значение в промежутке 0-1.
Благодаря тому, как обучается модель, предсказания логистической регрессии можно использовать для отображения вероятности принадлежности образца к классу 0 или 1. Это полезно в тех случаях, когда нужно иметь больше обоснований для прогнозирования.
Как и в случае с линейной регрессией, логистическая регрессия выполняет свою задачу лучше, если убрать лишние и похожие переменные. Модель логистической регрессии быстро обучается и хорошо подходит для задач бинарной классификации.
Выводы
Как можно наблюдать у каждого алгоритма машинного обучения для обнаружения неисправных чипов есть как достоинства, так и недостатки.
Достоинства логистической регрессии:
- логистическая регрессия проста в реализации и легче интерпретировать выходные коэффициенты;
- он не только позволяет оценить, насколько подходящим является предиктор (величина коэффициента), но и направление его связи (положительное или отрицательное).
- логистическая регрессия менее склонна к чрезмерной подгонке, но она может привести к чрезмерной подгонке в наборах данных с высокой размерностью. Можно рассмотреть методы регуляризации (L1 и L2), чтобы избежать чрезмерной подгонки в этих сценариях.
Список использованной литературы
- Вьюгин, В.В. Математические основы теории машинного обучения и прогнозирования / В.В. Вьюгин – М.: МОСКВА, 2013. – 387 с.
- Искусственный интеллект и машинное обучение, [Электронный ресурс], – Режим доступа: https://azure.microsoft.com/ru-ru/overview/artificial-intelligence-ai-vs-machine-learning/#introduction/
- Метод k-ближайших соседей (k-nearest neighbour), [Электронный ресурс], – Режим доступа: https://proglib.io/p/metod-k-blizhayshih-sosedey-k-nearest-neighbour-2021-07-19
- Айвазян, С. А. Прикладная статистика: классификация и снижение размерности / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин – М.: Финансы и статистика, 1989. – 248 с.
- Bartlett, P. Generalization performance of support vector machines and other pattern classifiers / P. Bartlett, J. Shawe-Taylor – Cambridge: MIT Press USA, 1998. – 189 с.