Ссылка: Челышев Э.А. Сравнение методов классификации русскоязычных новостных текстов с использованием алгоритмов машинного обучения / Э.А. Челышев, Ш.А. Оцоков, М.В. Раскатова, П. Щёголев // ВК. - 2022 г. - №1 (45) - С. 63-71 - [Ссылка]

Научная статья УДК 004.91

doi: 10.34822/1999-7604-2022-1-63-71

СРАВНЕНИЕ МЕТОДОВ КЛАССИФИКАЦИИ РУССКОЯЗЫЧНЫХ НОВОСТНЫХ ТЕКСТОВ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМОВ МАШИННОГО ОБУЧЕНИЯ

Эдуард Артурович Челышев1, Шамиль Алиевич Оцоков2, Марина Викторовна Раскатова3, Павел Щёголев4

1, 2, 3, 4Национальный исследовательский университет «МЭИ», Москва, Россия

1chel.ed@yandex.ru, http://orcid.org/0000-0001-8417-8823 2Shamil24@mail.ru, http://orcid.org/0000-0001-7451-5443 3marina@raskatova.ru, http://orcid.org/0000-0001-7671-3312 4Shchegolevsp@mpei.ru, http://orcid.org/0000-0001-9954-8858

Аннотация. В работе рассмотрена задача классификации русскоязычных новостных текстов с использованием таких алгоритмов машинного обучения, как наивный байесовский классификатор, случайный лес деревьев решений, логистическая регрессия и искусственная нейронная сеть. Для ре- шения задачи использовались тексты новостного интернет-портала Lenta.ru, относящиеся к девяти различным классам – рубрикам новостных статей. Программная реализация в рамках данной работы проводилась с использованием языка программирования Python. Проведена предварительная обра- ботка текстовых данных: удаление нерелевантных символов и приведение их к общему регистру, то- кенизация, нормализация, удаление стоп-слов и векторизация текстов. Для реализации искусственной нейронной сети в рамках данной работы использовались библиотеки Tensorflow и Keras языка про- граммирования Python. Для каждой из использованных моделей машинного обучения были опреде- лены значения гиперпараметров, дающих наивысшее качество классификации, с использованием ря- да метрик: precision, recall и F-мера. Проведен сравнительный анализ использованных алгоритмов. Указаны возможные пути дальнейшей работы в рамках рассматриваемой задачи.

Ключевые слова: классификация текстов, машинное обучение, корпус, токен, стоп-слово, лемматизация, искусственная нейронная сеть, качество классификации

Для цитирования: Челышев Э. А., Оцоков Ш. А., Раскатова М. В., Щёголев П. Сравнение методов классификации русскоязычных новостных текстов с использованием алгоритмов машинно- го обучения // Вестник кибернетики. 2022. № 1 (42). С. 63–71. DOI 10.34822/1999-7604-2022-1-63-71.

Original article

COMPARING CLASSIFICATION METHODS FOR NEWS TEXTS IN RUSSIAN USING MACHINE LEARNING ALGORITHMS

Eduard A. Chelyshev1, Shamil A. Otsokov2, Marina V. Raskatova3, Pavel Shchegolev4

1, 2, 3, 4National Research University “Moscow Power Engineering Institute”, Moscow, Russia

1chel.ed@yandex.ru, http://orcid.org/0000-0001-8417-8823 2Shamil24@mail.ru, http://orcid.org/0000-0001-7451-5443 3marina@raskatova.ru, http://orcid.org/0000-0001-7671-3312 4Shchegolevsp@mpei.ru, http://orcid.org/0000-0001-9954-8858

Abstract. The article discusses the problem of classification of news texts in Russian using such ma- chine learning algorithms as naive Bayes classifier, random decision forests, logistic regression, and artificial neural network. The texts of the Internet news portal Lenta.ru were selected from nine different classes – sections of news articles to solve the problem. The software implementation in the framework of the study was carried out using the Python programming language. The preprocessing of text data included removal of

irrelevant characters and their reduction to a common register, tokenization, normalization, removal of stop words and vectorization of texts. Tensorflow and Keras libraries of the Python programming language were used to implement an artificial neural network. For each of the machine learning models used, hyperparame- ters values were determined in order to achieve the highest classification quality using a number of metrics: precision, recall and F-measure. A comparative analysis of the algorithms used was carried out. Possible ways for further study within the problem in question are specified.

Keywords: text classification, machine learning, corpus, token, stop word, lemmatization, artificial neural network, classification quality

For citation: Chelyshev E. A., Otsokov Sh. A., Raskatova M. V., Shchegolev P. Comparing Classifi- cation Methods for News Texts in Russian Using Machine Learning Algorithms // Proceedings in Cybernet- ics. 2022. No. 1 (42). P. 63‒71. DOI 10.34822/1999-7604-2022-1-63-71.

ВВЕДЕНИЕ

Для современного мира характерен быст- рый рост объема информационных баз дан- ных, скорости обработки информации и объ- ема хранения данных [1]. Именно поэтому в последние годы все более популярными становятся средства автоматической обра- ботки информации, в том числе основанные на алгоритмах машинного обучения.

Для обработки естественного языка (англ. natural language processing) возможно приме- нение машинного обучения, которое исполь- зуется во многих сферах: перевод, поиск ин- формации, распознавание речи, определение ее строения и тональности, система элек- тронного документооборота и пр. [2].

Одной из задач обработки естественного языка является задача классификации тек- стов, которая может использоваться в но- востных агрегаторах, рубрикаторах научных текстов и пр. При этом стоит отметить, что автоматическая классификация текстов зна- чительно эффективнее ручной обработки больших объемов информации [3].

МАТЕРИАЛЫ И МЕТОДЫ

В работе был использован корпус новост- ных статей интернет-портала lenta.ru [4]. Условимся, что в дальнейшем в работе ста- тьи корпуса будут именоваться документа- ми. Для каждого документа приведены его содержание и заголовок, дата публикации и URL-ссылка на веб-страницу с оригиналь- ным текстом, рубрика (т. е. сфера обще- ственной жизни, к которой относится данная публикация). Из исходного корпуса были выделены документы, относящиеся к девяти рубрикам: «Дом», «Интернет и СМИ»,

«Культура», «Наука и техника», «Политика»,

«Путешествия», «Силовые структуры»,

«Спорт», «Экономика и бизнес». Из выде- ленных документов был сформирован итого- вый корпус.

Проведена предварительная обработка текстов документов, включающая следую- щие этапы: удаление нерелевантных симво- лов и приведение их к общему регистру, то- кенизация, нормализация, удаление стоп- слов и векторизация [5].

Удаление нерелевантных символов в дан- ной работе выполняли с использованием регулярных выражений. В качестве нереле- вантных рассматривали все символы, за ис- ключением буквенных и пробелов. Также были удалены присутствующие в тексте URL-ссылки. Все оставшиеся в текстах сим- волы были преобразованы в строчную фор- му. На этапе токенизации текст был разбит на отдельные токены, т. е. слова. Для выпол- нения нормализации использовали леммати- зацию [6], для лемматизации токенов – морфологический анализатор русского язы- ка, реализованный в библиотеке Pymorphy2 языка программирования Python [7]. Затем из числа токенов, преобразованных в ходе нормализации, были удалены стоп-слова, т. е. часто встречающиеся, но не несущие су- щественной лексической нагрузки слова [8].

Векторизация текстов проводилась в два этапа. На первом этапе каждому токену из документа корпуса устанавливали соответ- ствие его векторному представлению. На вто- ром – вычисляли векторное представление документа как среднее арифметическое век- торных представлений всех токенов, входя- щих в документ.

Векторизация токенов производилась с ис- пользованием модели векторизации FastText, предобученной на русскоязычных текстах [9]. Модели векторизации в сравнении с некото- рыми другими методами векторизации тек- стов (например, мешка слов) имеют ряд пре- имуществ. Во-первых, векторные представ- ления токенов, сгенерированные моделями векторизации, имеют размерность значитель- но меньшую, чем размерность используемого словаря. Так, например, в данной работе то- кенам, а следовательно, и документам стави-

лось в соответствие 300-мерное векторное

появления признаков задается нормальным распределением. Тогда вероятность того, что объект, обладающий значением 𝑥𝑖 неко- торого i-го признака, принадлежит классу

𝐶𝑘, задается с использованием формулы (1). Такой алгоритм называется гауссовским НБК (англ. Gaussian Naive Bayes) [12]. С уче- том особенностей выполненной векториза- ции текстового корпуса именно такая разно- видность НБК является подходящей для ре- шения рассматриваемой задачи:

2

𝑃(𝑥 |𝐶 ) = 1 exp (− (𝑥𝑖−𝜇𝑘) ),

представление. Во-вторых, модели вектори- зации учитывают семантические, т. е. смыс-

𝑖 𝑘

𝑘

√2𝜋𝜎2

𝑘

2𝜎2

(1)

ловые отношения токенов [10].

Подготовленные таким образом данные были разделены на обучающую и тестовую выборки, размер тестовой выборки составил 25 % от общего объема корпуса.

Постановка задачи. В работе рассматри- вается задача классификации новостных тек- стов. Учитывая проведенную предваритель- ную обработку текстов, данную задачу мож- но формализовать следующим образом: пусть имеется документ 𝑑𝑖 ∈ 𝐷, 𝑖 = 1, 2, . . .,

𝐾, где 𝐷 = {𝑑1, 𝑑2, … , 𝑑𝐾} – множество доку- ментов в корпусе, а 𝐾 – размерность корпу- са, причем документ представлен как вектор n-мерного векторного пространства, т. е.

𝑑 = (𝑣1, 𝑣2, … , 𝑣𝑛). В данной работе 𝑛 = 300. Пусть также задан некий фиксированный набор классов 𝐶 = {𝑐1, 𝑐2, … , 𝑐𝑚}. В данной работе 𝑚 = 9 по числу рубрик в итоговом корпусе.

Используя обучающую выборку с приме- нением метода обучения, необходимо полу- чить классифицирующую функцию 𝑔: 𝐷 → 𝐶, которая отображает множество документов

где 𝜎𝑘 – среднеквадратичное отклонение зна- чений i-го признака для объектов класса 𝐶𝑘;

𝜇𝑦 – математическое ожидание значений

i-го признака для объектов класса 𝐶𝑘.

В работе был также рассмотрен класси- фикатор на основе метода логистической ре- грессии (ЛР, англ. Logistic Regression). Данный метод является методом бинарной классификации и позволяет для каждого объ- екта получить значение вероятности принад- лежности данного объекта к каждому из клас- сов. Пусть одному классу соответствует зна- чение 𝑦 = −1, а другому – 𝑦 = +1, т. е. мно- жество возможных меток 𝑌 = {−1, +1}. Тогда вероятность того, что объект 𝑥 принадлежит классу 𝑦, определяется по формуле (2):

𝑃(𝑦|𝑥) = 𝜎(〈𝑤, 𝑥〉𝑦), (2) где 𝑤 – вектор весов;

〈𝑥, 𝑦〉 – скалярное произведение векторов

𝑥 и 𝑦;

𝜎(𝑧) – логистическая функция, опреде- ляемая по формуле (3):

во множестве классов [11].

Построение классификаторов. Первым

𝜎(𝑧) = 1 1+𝑒−𝑧

. (3)

рассмотренным классификатором в данной работе выступает наивный байесовский классификатор (НБК, англ. Naive Bayes), ко- торый строится на «наивном» предположе- нии о независимости признаков.

Если пространство признаков принимает- ся непрерывным, то при построении НБК зачастую предполагается, что вероятность

В случае, если классов более, чем два, задачу мультиклассификации можно рас- сматривать как ряд задач бинарной класси- фикации, каждую из которых можно решить, используя ЛР. Кроме того, метод ЛР может быть обобщен для задачи мультиклассифи- кации. Предположим, что в задаче муль- тиклассификации присутствует 𝑁 непересе-

кающихся классов. Тогда многоклассовая ЛР подразумевает построение набора из 𝑁 линейных моделей, каждая из которых имеет свой собственный вектор весов 𝑤𝑘, 𝑘 = 1, 2,

… , 𝑁. Затем для каждого объекта, используя построенные линейные модели, можно опре- делить численную оценку 𝑧𝑘 = 〈𝑤𝑘, 𝑥〉 принадлежности объекта к k-му классу. Для преобразования вектора численных оце- нок в вектор вероятностей используется функция Softmax, которая представляет со- бой многомерное обобщение логистической функции, т. е. вектор 𝑝 вероятностей при- надлежности объекта к каждому из классов вычисляется по формуле (4) [13]:

𝑝 = (𝑝1, 𝑝2, … , 𝑝𝑁) = S(𝑧1, z2, … , z𝑁) =

,

   exp(z1)        exp(zN)    (4)

( , … , )

бранные таким образом объекты в дальней- шем будут использоваться для обучения это- го ДР. Для каждого разветвления внутри ДР модель также случайным образом выбирает учитываемые признаки. Таким образом, воз- можное переобучение каждого из деревьев в отдельности на своем наборе данных ком- пенсируется за счет усреднения по множе- ству различных ДР [15].

При построении ДР был использован алго- ритм CART (англ. Classification and Regres- sion Tree). Для задания функционала качества при построении решающего дерева в данной работе использовался критерий информатив- ности Джини, который вычисляется по фор- муле (5), при этом нужно отметить, что, чем меньше критерий Джини для вершины ДР, тем меньше неопределенность в ней:

∑

∑

N

k=1

exp(zk)

N

k=1

exp(zk)

𝐺(𝑝) = 1 − ∑𝑛

𝑝2, (5)

где 𝑁 – количество классов в задаче муль- тиклассификации;

𝑝𝑘 – вероятность принадлежности к k-му классу.

В работе рассмотрен классификатор на основе алгоритма случайного леса (СЛ, англ. Random Forest) дерева решений (СЛДР). Стоит отметить, что сам по себе алгоритм на основе дерева решений (ДР) имеет суще- ственный недостаток, а именно склонность к переобучению. Переобучением называется нежелательное явление, при котором обу- ченный алгоритм машинного обучения на данных, не входящих в обучающую вы- борку, показывает качество значительно ху- же, чем на обучающей выборке. Причиной переобучения является излишне точное по- вторение алгоритмом зависимостей обуча- ющей выборки, из-за чего он теряет обоб- щающую способность в целом. По этой при- чине использование ансамблевого метода, такого как СЛДР, представляется более оправданным [14].

Алгоритм СЛДР заключается в построе- нии некоторого множества различных ДР на одном и том же наборе данных. На этапе обучения при построении каждого из дере- вьев в отдельности производится случайный выбор некоторого подмножества объектов внутри обучающей выборки. Именно вы-

𝑖=1 𝑖

где 𝑇 – набор объектов в вершине;

𝑛 – число классов, содержащихся в наборе 𝑇;

𝑝 = (𝑝1, 𝑝2, … , 𝑝𝑛) – вектор вероятностей (относительных частот) для каждого из клас- сов в наборе 𝑇.

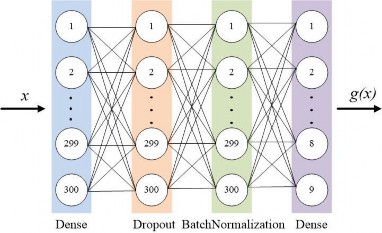
Последним использованным классифика- тором является искусственная нейронная сеть (ИНС), реализованная с использованием библиотек Tensorflow и Keras языка про- граммирования Python (рис. 1).

ИНС содержит четыре слоя. Входной слой является полносвязным. Он был реализован с использованием встроенного класса Dense библиотеки Keras. Входной слой содержит 300 нейронов по числу компонент векторно- го представления документа. Первый скры- тый слой был выполнен с использованием класса Dropout библиотеки Keras. Во время обучения ИНС данный слой случайным об- разом отключает некоторую долю своих нейронов, в результате чего уменьшается ве- роятность переобучения. Доля отключаемых нейронов определяется коэффициентом от- ключения, который также может рассматри- ваться как гиперпараметр модели. Второй скрытый слой был реализован с использова- нием класса BatchNormalization. Он осу- ществляет статистическую нормализацию выхода предыдущего слоя. В качестве функ-

ции активации на скрытых слоях использует- ся функция ReLU. Выходной слой также является полносвязным (класс Dense библио- теки Keras) и содержит 9 нейронов, каждый

из которых соответствует отдельной рубрике. Функция Softmax используется в качестве функции активации выходного слоя [16].

Рис. 1. Структура искусственной нейронной сети

Примечание: составлено авторами.

Оценка качества классификации.

Для оценки качества классификации были

𝐽𝑟

   𝐺+ , (7)

+ −

= 𝑝    

𝐺 +𝐺

использованы метрики precision (точность) 𝐽𝑝 и recall (полнота) 𝐽𝑟, определяемые форму- лами (6) и (7) соответственно. Метрика preci- sion является долей верно классифицирован- ных объектов в общем числе объектов, отне- сенных классификатором к данному классу. Метрика recall указывает, насколько полно классификатор распознал класс: чем меньше отношение числа объектов в классе, которые были ошибочно отнесены к другому классу, к числу объектов данного класса, тем выше значение метрики recall. В работе использо- валась также 𝐹β-мера, которая является ком- бинированной метрикой, в которой параметр β является весом метрики precision. Частным случаем данной метрики при β = 1 является

𝑝 𝑛

𝑝

где 𝐺+ – число объектов, для которых клас- сификатор верно определил принадлежность к текущему классу (англ. true positives);

𝑛

𝐺+ – число объектов, для которых клас- сификатор верно определил, что они не при- надлежат к текущему классу (англ. true negatives);

𝑝

𝐺− – число объектов, для которых класси- фикатор неверно определил, что они принад- лежат к текущему классу (англ. false positives);

𝑛

𝐺− – число объектов, для которых клас- сификатор неверно определил, что они не принадлежат к текущему классу (англ. false negatives).

𝐽𝑝×𝐽𝑟,

F1-мера 𝐽𝐹, определяемая формулой (8), ко-

𝐽𝐹 = 2 × 𝐽 +𝐽

(8)

торая и использовалась в данной работе. Также при обучении ИНС для контроля воз- можного переобучения использовалась мет-

𝐽𝑎

𝑝 𝑟

= (9)

𝑝        𝑛      

     𝐺++𝐺+ .

𝑝 𝑝 𝑛 𝑛

𝐺++𝐺−+𝐺++𝐺−

рика accuracy 𝐽𝑎, задаваемая формулой (9). Данная метрика равняется доле верно клас- сифицированных объектов в общем числе объектов всех классов [17]:

𝐺+

Рассмотренные выше метрики классифи- кации предназначены для бинарной класси- фикации. В случае мультиклассификации

данные метрики вычисляются для каждого класса в отдельности, после чего можно вы-

𝐽𝑝

=     𝑝  , (6)

+ −

𝐺 +𝐺

числить средние значения метрик как пока-

𝑝 𝑝

затели качества построенного классификато- ра в целом.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Программные реализации НБК, ЛР и СЛДР были взяты из библиотеки scikit-learn языка

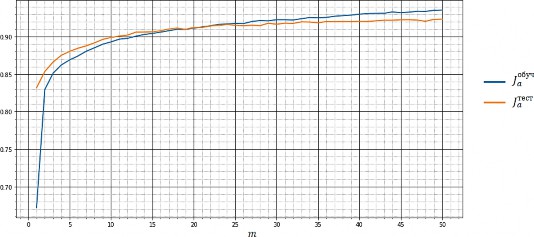
классификации были определены значения гиперпараметров, дающих наилучшее каче- ство классификации. Обучение ИНС велось при числе эпох 𝑚 = 50. В ходе обучения на каждой эпохе производили измерения величин

𝐽обуч и 𝐽тест, т. е. значений метрики accuracy на

𝑎 𝑎

программирования Python. С использованием алгоритма решетчатого поиска с применением скользящего контроля для данных моделей

обучающей и тестовой выборках соответ- ственно (рис. 2).

Рис. 2. Зависимость значений метрики accuracy от числа эпох

Примечание: составлено авторами на основе экспериментальных данных.

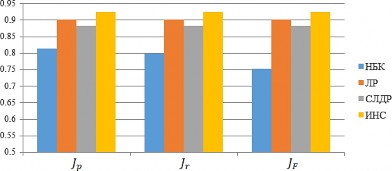
Для каждого из классификаторов были определены средние значения метрик клас-

сификации (табл. 1, рис. 3).

Таблица 1

Сводная таблица значений метрик классификации

Примечание: составлено авторами на основе экспериментальных данных.

Рис. 3. Гистограмма значений метрик классификации

Примечание: составлено авторами.

Видно, что наибольшие значения метрик классификации показали разработанная авто- рами ИНС и ЛР. При этом достаточно близ- кие к ним значения показал и СЛДР. Наив- ный байесовский классификатор как про-

стейшая модель при этом показал значитель- но более низкое качество классификации.

Проведем анализ двух классификаторов, показавших наилучшие результаты (табл. 2).

Таблица 2

Значения метрик классификации для ИНС и ЛР

Примечание: составлено авторами на основе экспериментальных данных.

На основании данных табл. 2 можно заклю- чить, что ИНС распознала лучше, чем ЛР во- семь классов (рубрик) из девяти. Исключением является только рубрика «Экономика и биз- нес», для которой наивысшие значения метрик классификации показала именно ЛР. Такой ре- зультат можно объяснить тем, что данная руб- рика являлась самой объемной в используемом наборе данных и была представлена наиболь- шим количеством документов.

ЗАКЛЮЧЕНИЕ

В ходе проведенного исследования рас- сматривалось решение задачи классификации русскоязычных новостных текстов с приме- нением алгоритмов машинного обучения. Использованный корпус документов (новост- ных статей) был предварительно обработан и каждому документу был поставлен в соот- ветствие вектор 300-мерного векторного про- странства. Были реализованы и обучены че- тыре классификатора: наивный байесовский классификатор, логистическая регрессия, случайный лес деревьев решений и предло-

женная коллективом авторов искусственная нейронная сеть. В целом наилучшее качество при этом показала именно искусственная нейронная сеть. При этом рубрика «Экономи- ка и бизнес» была распознана наилучшим об- разом логистической регрессией.

Однако задачу классификации текстов во- обще и новостных в частности нельзя счи- тать окончательно решенной. Стоит отме- тить, что в работе не использовались некото- рые другие алгоритмы классификации, например метод k ближайших соседей и ма- шина опорных векторов.

Авторы планируют продолжить исследо- вания в двух направлениях. Во-первых, при- рост качества классификации могут показать искусственные нейронные сети с другими архитектурами. Во-вторых, полезным может оказаться использование ансамблей различ- ных методов, как рассмотренных выше, так и тех, которые еще не были проанализи- рованы в данной работе.

Список источников

1. Reinsel D., Gantz J., Rydning J. The Digitalization of the World – From Edge to Core. IDC White Pa- per, 2018. 28 p. URL: https://www.seagate.com/ files/www-content/our-story/trends/files/idc-seagate- dataage-whitepaper.pdf (дата обращения: 11.01.2022).

   References

   1. Reinsel D., Gantz J., Rydning J. The Digitalization of the World – From Edge to Core. IDC White Pa- per, 2018. 28 p. URL: https://www.seagate.com/ files/www-content/our-story/trends/files/idc-seagate- dataage-whitepaper.pdf (accessed: 11.01.2022).

   2. Батура Т. В. Методы автоматической классифи- кации текстов // Программн. продукты и систе- мы. 2017. Т. 30, № 1. С. 85–99.

   3. Шаграев А. Г. Модификация, разработка и реали- зация методов классификации новостных текстов : дис. … канд. техн. наук. М., 2014. 108 с.

   4. News Dataset from Lenta.ru. URL: https://www.kag gle.com/yutkin/corpus-of-russian-news-articles-from- lenta (дата обращения: 08.02.2022).

   5. Челышев Э. А., Оцоков Ш. А., Раскатова М. В. Автоматическая рубрикация текстов с использо- ванием алгоритмов машинного обучения // Вестн. Рос. нового ун-та. Сер.: Сложные систе- мы: модели, анализ, управление. 2021. № 4. С. 175–182. DOI 10.25586/RNU.V9187.21.04.P.175.

   6. Вершинин Е. В., Тимченко Д. К. Исследование применения стемминга и лемматизации при раз- работке систем адаптивного перевода текста // Наука. Исследования. Практика : сб. изб. ст. по материалам Междунар. науч. конф. СПб. : Гума- нитар. национал. исслед. ин-т «НАЦРАЗВИ- ТИЕ», 2020. С. 77–79.

   7. Korobov M. Morphological Analyzer and Generator for Russian and Ukrainian Languages // Proceedings of the 4th International Conference, AIST 2015, Ye- katerinburg, Russia, April 9–11, 2015. P. 330–342. DOI 10.1007/978-3-319-26123-2_31.

   8. Мартынов В. А., Плотникова Н. П. Нормализа- ция и фильтрация текста для задачи кластериза- ции // XLVIII Огаревские чтения : материалы науч. конф. В 3 ч. Саранск, 06–13 декабря 2019 г. Саранск : Национал. исслед. Мордов. гос. ун-т им. Н. П. Огарева, 2020. С. 448–452.

   9. Korogodina O., Klyshinsky E., Karpik O. Evaluation of Vector Transformations for Russian Word2Vec and FastText Embeddings // Proceedings of the 30th International Conference on Computer Graphics and Machine Vision (GraphiCon 2020). Part 2. Saint Pe- tersburg, 2020.

   10. Жеребцова Ю. А., Чижик А. В. Сравнение моде- лей векторного представления текстов в задаче создания чатбота // Вестник НГУ. Сер.: Лингви- стика и межкультурная коммуникация. 2020. Т. 18, № 3. С. 16–34. DOI 10.25205/1818-7935-

       2020-18-3-16-34.

   11. Рубцова Ю. С. Методы и алгоритмы построения информационных систем для классификации текстов социальных сетей по тональности : дис. … канд. техн. наук. Новосибирск, 2019. 141 с.

   12. Fadlil A., Riadi I., Aji S. DDoS Attacks Classifica- tion Using Numeric Attribute-Based Gaussian Naive Bayes // International Journal of Advanced Comput- er Science and Applications. 2017. No. 8. P. 42–50. DOI 10.14569/IJACSA.2017.080806.

   13. Aggarwal C. C., Zhai C. Mining Text Data. Boston : Springer, 2012. 524 p.

   14. Полин Я. А., Зудилова Т. В., Ананченко И. В., Войтюк Т. Е. Деревья решений в задачах класси- фикации: особенности применения и методы по- вышения качества классификации // Современ.

2. Batura T. V. Automatic Text Classification Methods // Software & Systems. 2017. Vol. 30, No. 1. P. 85–99. (In Russian).

3. Shagraev A. G. Modifikatsiia, razrabotka i realizatsi- ia metodov klassifikatsii novostnykh tekstov : Cand. Sci. Dissertation (Engineering). Moscow, 2014. 108 p. (In Russian).

4. News Dataset from Lenta.ru. URL: https://www.kag gle.com/yutkin/corpus-of-russian-news-articles-from- lenta (accessed: 08.02.2022).

5. Chelyshev E. A., Otsokov Sh. A., Raskatova M. V. Automatic Text Rubrication Using Machine Learn- ing Algorithms // Vestnik of Russian New Universi- ty. Series: Complex Systems: Models, Analysis, Management. 2021. No. 4. P. 175–182. DOI 10.25586/RNU.V9187.21.04.P.175. (In Russian).

6. Vershinin E. V., Timchenko D. K. Research of the Application of Stemming and Lemmatization Apply- ing to Adaptive Text Translation System // Nauka. Issledovaniia. Praktika : Collection of selected arti- cles in proceedings of the International Research Conference. Saint Petersburg : Gumanitar. national. issled. in-t “NATsRAZVITIE”, 2020. P. 77–79. (In

   Russian).

7. Korobov M. Morphological Analyzer and Generator for Russian and Ukrainian Languages // Proceedings of the 4th International Conference, AIST 2015, Ye- katerinburg, Russia, April 9–11, 2015. P. 330–342. DOI 10.1007/978-3-319-26123-2_31.

8. Martynov V. A., Plotnikova N. P. Text Normaliza- tion and Filtration for Clustering Task // XLVIII Og- arevskie chteniia : Proceedings of the Research Con- ference. In 3 parts. Saransk, December 6‒13, 2019. Saransk : Ogarev Mordovia State University, 2020.

   P. 448–452. (In Russian).

9. Korogodina O., Klyshinsky E., Karpik O. Evaluation of Vector Transformations for Russian Word2Vec and FastText Embeddings // Proceedings of the 30th International Conference on Computer Graphics and Machine Vision (GraphiCon 2020). Part 2. Saint Pe- tersburg, 2020.

10. Zherebtsova Yu. A., Chizhik A. V. Text Vectoriza- tion Methods for Retrieval-Based Chatbot // NSU Vestnik. Series: Linguistics and Intercultural Com- munication. 2020. Vol. 18, No. 3. P. 16–34. DOI 10.25205/1818-7935-2020-18-3-16-34. (In Russian).

11. Rubtsova Yu. S. Metody i algoritmy postroeniia informatsionnykh system dlia klassifikatsii tekstov sotsialnykh setei po tonalnosti : Cand. Sci. Disserta- tion (Engineering). Novosibirsk, 2019. 141 p. (In Russian).

12. Fadlil A., Riadi I., Aji S. DDoS Attacks Classifica- tion Using Numeric Attribute-Based Gaussian Naive Bayes // International Journal of Advanced Comput- er Science and Applications. 2017. No. 8. P. 42–50. DOI 10.14569/IJACSA.2017.080806.

13. Aggarwal C. C., Zhai C. Mining Text Data. Boston : Springer, 2012. 524 p.

14. Polin Ya. A., Zudilova T. V., Ananchenko I. V., Voityuk T. E. Decision Trees in Classification Prob-

    наукоемкие технологии. 2020. № 9. С. 59–63. DOI 10.17513/snt.38215.

15. Bertsimas D., Dunn J. Optimal classification trees // Machine Learning. 2017. Vol. 106. P. 1039–1082.

16. Челышев Э. А., Оцоков Ш. А., Раскатова М. В. Разработка информационной системы для автома- тической рубрикации новостных текстов // Меж- дунар. журн. информацион. технологий и энер- гоэффективности. 2021. Т. 6, № 3 (21). С. 11–17.

17. Vujovic Z. D. Classification Model Evaluation Met- rics // International Journal of Advanced Computer Science and Applications. 2021. Vol. 12, No. 6.

P. 599–606.

lems: Application Features and Methods for Improv- ing the Quality of Classification // Modern High Technologies. 2020. No. 9. P. 59–63. DOI 10.17513/snt.38215. (In Russian).

1. Bertsimas D., Dunn J. Optimal Classification Trees // Machine Learning. 2017. Vol. 106. P. 1039–1082.

2. Chelyshev E. A., Otsokov Sh. A., Raskatova M. V. Development of Information System for Automatic Rubrication of News Texts // Mezhdunar. zhurn. in- formation. tekhnologii i energoeffektivnosti. 2021. Vol. 6, No. 3 (21). P. 11–17. (In Russian).

3. Vujovic Z. D. Classification Model Evaluation Metrics // International Journal of Advanced Com- puter Science and Applications. 2021. Vol. 12, No. 6. P. 599–606.

Информация об авторах

Э. А. Челышев – магистрант.

Ш. А. Оцоков – доктор технических наук.

М. В. Раскатова – кандидат технических наук.

П. Щёголев – ассистент.

Information about the authors

E. A. Chelyshev – Master’s Degree Student.

Sh. A. Otsokov – Doctor of Sciences (Engineering).

M. V. Raskatova – Candidate of Sciences (Engi- neering).

P. Shchegolev – Assistant Professor.