Введение
В нашей работе мы пытаемся выделить основной смысл текста на естественном языке (ЕЯ). Для достижения этой цели мы предлагаем проводить кластеризацию текста с помощью муравьиных алгоритмов.
Обработка текста состоит из следующих этапов:
Получение взвешенного графа связности слов, входящих в текст.
Обработка графа при помощи муравьиного алгоритма.
Кластеризация.
Упрощение графа и проецирование его на плоскость для визуализации. Рассмотрим перечисленные этапы более подробно.
Получение семантической сети
Для построения семантической сети на основе текста на ЕЯ мы используем возможности ресурса AOT.ru [1], а именно синтаксический и семантический анализ. Синтаксический анализ даёт нам основные формы слов, составляющих текст, и их принадлежность к частям речи. Семантический анализ обнаруживает связи между словами, обусловленные конструкцией предложений.
Например, из предложения «Леса дают кров многим животным» мы получаем информацию, представленную на Рис. 1. Следует отметить, что в данном примере мы не учитываем направленность и смысловую нагрузку полученных связей.
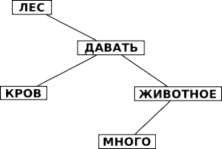
Рис. 1. Результат семантического анализа предложения.
Таким образом мы разбираем каждое предложение обрабатываемого текста, получая в итоге граф связности всех использованных в тексте слов. Веса (или длины) рёбер этого графа мы рассчитываем, исходя из значений повторности — количества извлечённых из текста связей между двумя словами. Длина ребра между любыми двумя связанными словами обратно пропорциональна повторности данной связи. Таким образом, длины всех рёбер находятся в промежутке (0, 1], причём чем выше повторность связи (чаще обнаруживается связь между словами в тексте), тем меньше её длина.
Муравьиные алгоритмы
Муравьиные алгоритмы — метод оптимизации, базирующийся на моделировании поведения колонии муравьев [2]. Основу «социального» поведения муравьев составляет самоорганизация
множество динамических механизмов, обеспечивающих достижение системой глобальной цели в результате низкоуровневого взаимодействия её элементов. Принципиальной особенностью такого взаимодействия является использование элементами системы только локальной информации. При этом исключается любое централизованное управление и обращение к глобальному образу, представляющему систему во внешнем мире. Самоорганизация является результатом взаимодействия следующих четырех компонентов:
Случайность;
Многократность;
Положительная обратная связь;
Отрицательная обратная связь.
Для применения муравьиных алгоритмов к представленной задаче необходимо соответствующим образом уточнить реализацию четырех составляющих самоорганизации муравьёв. В данной работе было предложено конкретизировать алгоритм следующим образом.
Многократность взаимодействия реализуется итерационным движением по графу взаимосвязей слов текста нескольких муравьёв. Каждый муравей начинает маршрут из своей точки — слова.
Положительная обратная связь реализуется как имитация поведения муравьев типа
«оставление следов — перемещение по следам». Для данной задачи это поведение подчиняется следующему стохастическому правилу: вероятность выбора ребра в качестве следующего в пути пропорциональна количеству феромона (следа, оставленного ранее другим муравьём) на нём. Применение такого вероятностного правила обеспечивает реализацию и другой составляющей самоорганизации — случайности. Количество откладываемого муравьём феромона на ребре графа связности обратно пропорционально длине ребра, а в начале работы алгоритма количество феромона на рёбрах принимается равным некоторому небольшому числу.
Использование только положительной обратной связи приводит к случаю, когда все муравьи двигаются одним и тем же маршрутом. Во избежание этого используется отрицательная обратная связь — испарение феромона. Время испарения не должно быть слишком большим, так как при этом возникает опасность сходимости популяции маршрутов к одному. С другой стороны, время испарения не должно быть и слишком малым, так как это приводит к быстрому
«забыванию», потере памяти колонии и, следовательно, к разобщённому поведению муравьев.
Кластеризация
В результате работы муравьиного алгоритма мы имеем граф связности базы знаний с некоторым количеством феромона на его рёбрах. В представленной работе мы предлагаем использовать эти данные для кластеризации слов обрабатываемого текста. Рассмотрим два способа кластеризации:
на основании длины связей;
на основании количеств а феромона на связях.
Для обоих вариантов кластеризация начинается с выбора ребра с максимальным (или близким к максимальному) количеством феромона на нём — оно будет являться начальной точкой распространения очередного кластера. При этом хотя бы одно слово из тех, что соединяет это ребро, не должно быть на текущий момент отнесено ни к одному кластеру. Понятия, которые связывает выбранное ребро, становятся элементами кластера.
Дальнейшее распространение кластера происходит по рёбрам, исходящим из первых двух слов, причём включение очередной связи (и, соответственно, слова на другом её конце) в кластер зависит от варианта кластеризации. Для кластеризации по длине связей ограничением является суммарная длина связей от одного из двух начальных слов до рассматриваемого слова. Для кластеризации по количеству феромона ограничена сумма величин, обратно пропорциональных количеству феромона на рёбрах, входящих в граф связей (чем больше количество феромона на связи, тем меньше включение её в состав кластера приближает нас к границе).
Использование такой модели кластеризации позволяет формировать пересекающиеся кластеры, что соответствует представлению о человеческом знании как о наборе некоторых смежных областей информации.
Выделенные из текста кластеры также сообщают нам семантическую структуру текста. Каждый полученный кластер можно считать одной из его смысловых частей, а центральный, через который осуществляется связь между кластерами, — основной идеей, вокруг которой построен текст.
Визуализация текста
Полученная в результате кластеризации информация позволяет упростить представление обрабатываемого текста. В частности, становится возможным не рассматривать слова, не вошедшие ни в один кластер, как имеющие малое значение для данного случая. Также можно исключить из рассмотрения связи, на которых по результатам работы муравьиного алгоритма осталось малое по сравнению со средним количество феромона.
После упрощения мы предлагаем визуализировать граф связности путём проецирования на плоскость. При этом сохраняется его многомерная пространственная структура за счёт применения градиентного метода наискорейшего спуска [3]. В результате имеем универсальное, простое для восприятия изображение, которое в то же время несёт в себе всю полученную из текста информацию — взаимосвязь и степень близости слов.