Аннотация

Лосев Д. Д., Зеленский Д. М. Применение методов математического моделирования в компьютерных сетях. Статья рассматривает современные вызовы и требования к проектированию и обновлению компьютерных сетей в условиях быстрого развития аппаратно-программных средств. Основное внимание уделяется важности математического моделирования и анализу производительности через теорию массового обслуживания. Используются аналитические и имитационные методы на примере исследования маршрутизатора.

Ключевые слова: математическое моделирование, проектирование, имитация, компьютерная сеть, оптимизация.

Введение

Аппаратно-программные средства вычислительной техники, объединенные в компьютерные сети, обновляются с большой скоростью и требуют обновления проектов сети в короткие сроки и с меньшими затратами.

Важнейшей характеристикой сети является односторонняя задержка пакетов (One-Way Delay Metric, OWD) входящая в число стандартов IPPM и описанная в RFC 2679. Единичное значение этой метрики описывается как время передачи пакета определенного типа между некоторыми двумя узлами сети.

Для оценки производительности проектируемой сети требуется определенный механизм предсказаний. Стохастический характер поступления данных и недетерминированная обработка в узлах коммутации и каналах связи предопределяет использование моделей теории массового обслуживания для проектирования и анализа проектных характеристик компьютерной сети. Теория массового обслуживания обеспечивает возможность расчета характеристик качества функционирования сетей, включая оценку вероятностно-временных характеристик узлов коммутации.

При изменении структуры сети в целях улучшения характеристик появляется опасность снижения надежности функционирования. Для оценки надежности сложной системы, такой как компьютерная сеть, применяется коэффициент оперативной готовности, показатель доли времени, в течение которого сеть работоспособна. Надежность может быть повышена путем введения избыточности в структуру системы: ключевые элементы должны существовать в нескольких экземплярах, чтобы при отказе одного из них функционирование системы обеспечивали резервные элементы [1].

Целью данной работы является исследование методов математического моделирования для оптимизации проектирования компьютерных сетей.

1 Математическое моделирование в компьютерных сетях

Моделирование – метод научного познания, при котором исследуемый объект заменяется более простым – моделью. Существуют физическое (натурное) и математическое моделирование. Физическое моделирование использует материальные системы для воссоздания свойств изучаемой системы, но оно ограничено и требует больших ресурсов. Например, проверка вычислительной сети с разными типами устройств — задача трудоемкая и дорогостоящая.

При изменении параметров системы проведение практических экспериментов в реальном времени для множества сочетаний этих параметров практически невозможно за разумное время. Например, даже изменение размера пакета в протоколе требует переконфигурирования операционной системы в сотнях компьютеров сети, что требует значительных усилий администратора.

Поэтому при оптимизации сетей часто предпочтительно использование математического моделирования. Математическая модель представляет собой совокупность уравнений, определяющих изменение состояния системы от параметров, входных сигналов, начальных условий и времени. Это позволяет анализировать множество сочетаний параметров без затрат, характерных для физического моделирования [2].

Аналитические модели — это тип математических моделей, используемых для анализа систем. Они строятся на основе аналитических выражений, уравнений и формул. Они позволяют проводить теоретический анализ и получать аналитические решения для характеристик системы.

В контексте вычислительных сетей аналитические модели могут использоваться для предсказания производительности, оценки надежности, и анализа различных параметров. Например, аналитические модели могут быть применены для определения пропускной способности сети, времени отклика, или вероятности потери пакетов.

Аналитическим методам при изучении телекоммуникационных систем посвящена отдельная дисциплина — Теория телетрафика.

Существует класс объектов, для которых по различным причинам не разработаны аналитические модели. В этом случае аналитическая модель заменяется имитационной. Имитационные модели, относятся к особому классу математических моделей. Они представляют собой компьютерные программы, которые последовательно воспроизводят события в реальной системе. В области вычислительных сетей эти модели подробно эмулируют процессы, такие как генерация сообщений, разбиение на пакеты, задержки в обработке, доступ к разделяемой сетевой среде, обработка пакетов маршрутизатором и многое другое. Уникальность имитационного моделирования заключается в отсутствии необходимости приобретать дорогостоящее оборудование – его функциональность эмулируется программами, достаточно точно воспроизводящими все ключевые особенности и параметры такого оборудования.

Преимущества имитационных моделей заключаются в возможности замены процесса смены событий в реальной системе на ускоренный процесс в темпе работы программы. Это позволяет воспроизвести работу сети за короткое время, что дает возможность оценить ее производительность в широком диапазоне варьируемых параметров. Результаты работы имитационной модели включают собранные в ходе наблюдения за событиями статистические данные о важных характеристиках сети, таких как времена реакции, коэффициенты использования каналов и узлов, вероятности потерь пакетов и прочее.

Существуют специальные языки имитационного моделирования, которые облегчают процесс создания программной модели по сравнению с использованием универсальных языков программирования. Примерами языков имитационного моделирования могут служить такие языки, как SIMULA, GPSS, SIMDIS. Существуют также системы имитационного моделирования, которые ориентируются на узкий класс изучаемых систем и позволяют строить модели без программирования.

Используя моделирование при проектировании или реинжинеринге локальной или глобальной сети, возможно осуществить следующее:

• оценить пропускную способность сети и ее компонентов;
• определить "узкие" места в структуре вычислительной системы;
• сравнить различные варианты организации вычислительной системы;
• осуществить перспективный прогноз развития вычислительной системы;
• предсказать будущие требования по пропускной способности сети, используя данные прогноза;
• оценить требуемое количество и производительность серверов в сети;
• сравнить различные варианты модернизации вычислительной системы;
• станций или серверов, изменения сетевых протоколов и многое другое.

Исследование параметров вычислительной системы при различных характеристиках отдельных компонентов позволяет выбрать сетевое и вычислительное оборудование с учетом производительности, качества обслуживания, надежности и стоимости.

2 Особенности проектирования компьютерной сети

Процесс проектирования компьютерной сети носит итерационный характер. Итерации могут включать в себя более чем один уровень проектирования. То есть, в процессе проектирования приходится многократно выполнять процедуру анализа объекта. Поэтому очевидно стремление уменьшить трудоемкость каждого варианта анализа без ущерба для качества окончательного проекта. В этих условиях целесообразно на начальных стадиях проектирования, когда высокой точности результатов не требуется, использовать наиболее простые и экономичные модели.

Создать проект сети означает выбрать структуру сети, определить значения всех его параметров и представить результаты в установленной форме. Результаты (проектная документация) могут быть выражены в виде схем, пояснительных записок, программ и других документов на бумаге или на машинных носителях информации.

Разработка (или выбор) структуры сети есть проектная процедура структурного синтеза, а расчет (или выбор) значений параметров элементов процедура параметрического синтеза.

Задача структурного синтеза заключается в определении цели, множества возможных решений и ограничивающих условий. Задача заключается в синтезе (или коррекции) структуры, определении типов серверов (программно-аппаратных средств), распределении функций по серверам таким образом, чтобы достигался экстремум целевой функции при выполнении заданных ограничений.

Следующая после синтеза группа проектных процедур – процедуры анализа. Цель анализа – получение информации о характере функционирования и значениях выходных параметров при заданных структуре объекта, сведениях о внешних параметрах и параметрах элементов.

Для анализа компьютерной сети широко используются математические методы и модели массового обслуживания. Упрощенные модели массового обслуживания позволяют находить явный вид целевой функции, в качестве которой используется характеристика сети, такая как время задержки сообщений (пакетов).

Моделирование жизненного цикла компьютерной сети проводится по итеративной модели – это выполнение работ параллельно с непрерывным анализом полученных результатов и корректировкой предыдущих этапов работы. Компьютерная сеть при этом подходе в каждой стадии проходит повторяющийся цикл: планирование – реализация – проверка – оценка (англ. plan-do-check-act cycle).

В автоматизированных проектных процедурах вместо проектируемого еще не существующего объекта оперируют моделью, которая отражает некоторые интересующие исследователя свойства объекта.

Математические функциональные модели в общем случае представляет собой алгоритм вычисления вектора выходных параметров при заданных векторах параметров элементов и внешних параметров.

Закон функционирования сети может быть представлен в следующем виде:

H(t) = fc(S, F, Y , X, t),

где fс – функция, функционал, логические условия, алгоритм, методика, таблица или словесное описание, определяющее правило (закон) преобразования входных величин (параметров) в выходные величины (характеристики);

H(t) – вектор характеристик, зависящий от текущего момента времени t (t≥0):

H = {V, T, N, C, Z}.

Параметры – первичные данные сети: S – структурные, F – функциональные, Y – нагрузочные, X – внешней среды.

Характеристики – вторичные данные сети: V – мощностные, T – временные, N – надежностные, C – экономические, Z – прочие [1].

3 Исследование маршрутизатора сети коммутации пакетов методами имитационного и аналитического моделирования

Проведем исследование маршрутизатора методами имитационного и аналитического моделирования.

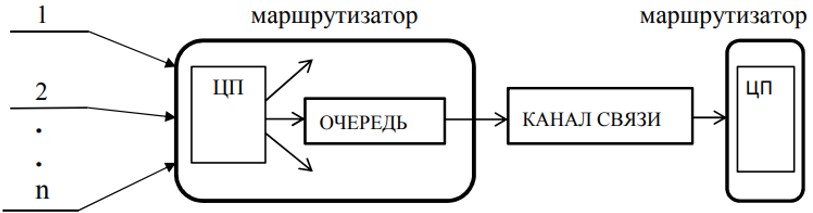
В интересующей нас части, маршрутизатор работает следующим образом:

• все пакеты входящие из разных направлений поступают в центральный процессор (или специализированный процессор выбора пути), который выбирает канал (направление) дальнейшей передачи пакета;
• при наличии свободных каналов, процессор немедленно приступает к передаче пакета;
• если канал занят, то пакет ставится в соответствующую очередь и будет передан по мере освобождения канала.

В теории телетрафика такой вид обслуживания классифицируется как обслуживание с неявными потерями, а конкретнее – обслуживание с очередями.

Основными характеристиками, определяющими качество функционирования сетей передачи данных, как и любых сетей с коммутацией пакетов, являются длительности задержек пакетов, включая джиттер, и вероятности потерь пакетов. Источниками задержек и потерь являются узлы коммутации (маршрутизаторы и коммутаторы) и каналы связи, через которые эти пакеты передаются. Каждый узел или канал, встречающиеся на пути продвижения пакета, вносят свою долю в эти характеристики.

Ниже приводятся методики определения основных вероятностно-временных характеристик маршрутизатора с помощью аналитической и имитационной моделей.

Аналитическая модель

Возможности аналитического моделирования более ограничены по сравнению с имитационным, поэтому ограничимся расчётом двух характеристик: средняя длина очереди пакетов и среднее время обслуживания пакета маршрутизатором, которое состоит из времени ожидания обслуживания и времени передачи пакета по каналу. При этом в обеих моделях рассматривается только система М/M/1/∞ (одноканальная система с пуассоновским потоком пакетов на входе, экспоненциальным распределением времени обслуживания при бесконечной очереди).

Эти характеристики легко рассчитываются по формулам Хинчина-Полячека и Литтла, которые для системы М/М/1/∞ принимают следующий вид:

q = ρ/(1 – ρ) и tq = q/λ,

где q – средняя длина очереди в рассматриваемой системе,

λ – интенсивность входного потока пакетов к рассматриваемому каналу,

t – средняя длительность обслуживания (передачи пакета по каналу),

(ρ = λt) – нагрузка одноканальной системы массового обслуживания,

tq - среднее время обслуживания пакета.

Имитационная модель

Моделирующая программа написана на языке GPSS и представлена ниже.

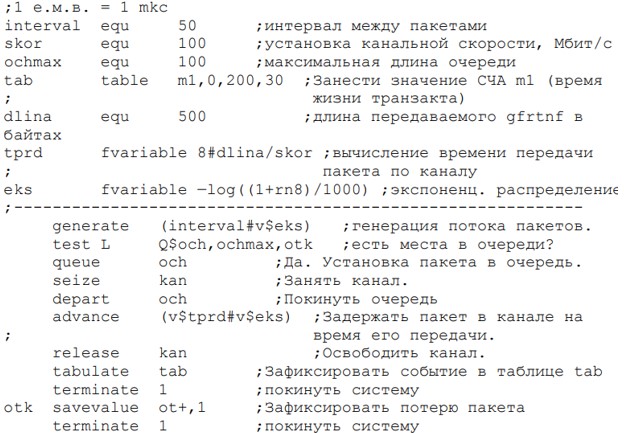
В исходной версии модель характеризуется следующими параметрами:

• Входной поток пакетов λ = 20 кПакетов/с.

В моделях GPSS генерация потоков пакетов (транзактов) определяется в операторе generate операндом А как интервал между моментами поступления пакетов t_инт, который подсчитывается как t_инт = 1/λ = 1/ 2*104 = 50 мкс.

В GPSS все временные интервалы задаются в единицах модельного времени (е.м.в.), а в данной программе принято 1 е.м.в. = 1 мкс. Поэтому в первом операторе (эквивалент) метке interval присвоено значение 50 е.м.в. Это значение используется в операторе generate совместно с функцией экспоненциального распределения этих интервалов.

• Канальная скорость задаётся вторым оператором. В исходном варианте установлена скорость 100 Мбит/с.
• В третьем операторе установлен максимально допустимый размер очереди пакетов (объём буферного накопителя). В исходном варианте установлена максимальная длина очереди – 100 пакетов.
• В четвёртом операторе устанавливается средняя длина передаваемых пакетов в байтах, а в следующем операторе в зависимости от этой длины и канальной скорости skor вычисляется среднее время передачи пакета по каналу в е.м.в. Это среднее время (метка tprd) совместно c экспоненциальной функцией распределения используется в операторе advance для задержки пакета на время его передачи по каналу.

Здесь необходимо отметить, что экспоненциальное распределение допускает появление в серии опытов с бесконечно малой вероятностью бесконечно большой величины (в нашем случае длины пакета). Реальные же технологии всегда ограничивают длину пакетов (кадров) какой-либо аргументированной величиной. Например, в АТМ это 53 байта, в Ethernet – 1500 байт, в Frame Relay – 4500 байт, а в IP-пакете версии IPv4 длина пакета ограничена только размером поля в заголовке пакета, указывающим на его длину. Это поле состоит из 2-х байтов и, следовательно, длина пакета не может превысить 65535 байт [3].

Выводы

В статье рассмотрены математические методы, применяемые для моделирования в компьютерных сетях. Особое внимание уделяется аналитическим и имитационным методам. Рассмотрены преимущества и ограничения этих методов. Также приведен пример исследования маршрутизатора с использованием аналитического подхода и имитационного подхода с использованием языка GPSS.

Список использованной литературы

1. Платунова, С. М. Методы проектирования фрагментов компьютерной сети: учебное пособие / С. М. Платунова. – Санкт-Петербург: НИУ ИТМО, 2012. – 51 с.
2. Моделирование сетей и систем связи [Электронный ресурс] // siblec.ru. - Электрон. дан. - 2020. - Режим доступа: https://siblec.ru/telekommunikatsii/modelirovanie-setej-i-sistem-svyazi#7 - Загл. с экрана
3. Нерсесянц А. А. Моделирование инфокоммуникационных систем и сетей связи: учебное пособие / А. А. Нерсесянц. – Ростов-на-Дону: СКФ МТУСИ, 2016. – 115 с.