Прогнозирование пассажиропотока общественного транспорта с помощью алгоритмов машинного обучения

Общая постановка проблемы

Прогнозирование пассажиропотока общественного транспорта является одной из ключевых задач для эффективного управления и планирования транспортных систем. Сложность этой проблемы обусловлена множеством факторов, влияющих на пассажиропоток, таких как время суток, день недели, сезонные колебания, погодные условия и различные городские события. Традиционные методы прогнозирования часто не способны адекватно учитывать все эти параметры, что приводит к неточным предсказаниям и, как следствие, к неэффективному использованию транспортных ресурсов.

Эффективное прогнозирование пассажиропотока имеет важное значение как с научной, так и с практической точки зрения. С научной точки зрения, это сложная задача, требующая применения передовых методов анализа данных и алгоритмов машинного обучения для обработки большого объема информации и выявления скрытых закономерностей. С практической стороны, точные прогнозы пассажиропотока позволяют оптимизировать расписание движения общественного транспорта, снизить затраты на его эксплуатацию, повысить комфорт пассажиров и уменьшить нагрузку на транспортную инфраструктуру города.

На сегодняшний день существует множество исследований, посвященных прогнозированию пассажиропотока с использованием различных подходов, включая статистические методы, регрессионные модели, методы временных рядов и алгоритмы машинного обучения. В частности, нейронные сети, такие как рекуррентные нейронные сети (RNN) и их модификации, например, долговременная краткосрочная память (LSTM), показали высокую эффективность в задачах прогнозирования временных рядов благодаря своей способности учитывать зависимости на длинных интервалах времени. Однако большинство существующих решений сосредоточено на краткосрочном прогнозировании (на день или несколько дней вперед) и редко учитывает данные за длительный период, что ограничивает их применимость в долгосрочном планировании. Кроме того, не все подходы в достаточной степени учитывают влияние внешних факторов, таких как погодные условия или городские события, что также может снижать точность прогнозов. Несмотря на значительные достижения в области прогнозирования пассажиропотока, остаются нерешенными несколько ключевых вопросов:

• Адаптация моделей к данным за длительный период – «Как эффективно использовать данные пассажиропотока за некоторый прошлый промежуток времени для повышения точности прогнозов?»;
• Интеграция внешних факторов – «Как лучше учитывать влияние внешних факторов, таких как погода и городские события, на пассажиропоток?»;
• Выбор и настройка алгоритмов – «Какие алгоритмы машинного обучения и их настройки показывают наилучшие результаты в условиях конкретного города и маршрутов?»

Целью статьи является изучение алгоритмов для построения модели машинного обучения для прогнозирования пассажиропотока общественного транспорта, а также изучение этапов ее разработки. Модель должна учитывать временные и внешние факторы для повышения точности прогнозов на следующее полугодие. Основные задачи исследования включают:

• Анализ существующих методов прогнозирования пассажиропотока и выделение наиболее оптимальных алгоритмов для поставленной задачи;
• Рассмотрение этапов создания модели, способной обрабатывать большие объемы данных и учитывать различные факторы, влияющие на пассажиропоток;
• Изучение способов оценки точности модели, а также методов ее улучшения;
• Разработка рекомендаций по применению модели в реальных условиях для улучшения управления городскими транспортными системами

Исследования

В статье рассмотрены методы, используемые для подготовки данных, построения и обучения модели. Для построения модели будут использоваться данные о пассажиропотоке, включающие следующие параметры: дата и время, количество пассажиров, маршрут (начальная и конечная остановка), внешние факторы (погода, городские события, праздники и т.д.).

Данные могут быть собраны из различных источников, включая транспортные компании и метеорологические службы. Перед обучением модели должна быть проведена предварительная обработка данных: очистка данных, нормализация данных (приведение всех числовых значений к одному масштабу для улучшения сходимости алгоритмов обучения), интеграция внешних факторов (добавление данных о погодных условиях, праздниках и городских событиях).

Для корректировки и улучшения качества датасета можно использовать следующие алгоритмы и методы [1]:

• Методы заполнения пропусков: KNN (метод ближайших соседей) и среднее значение для временных рядов;
• Анализ временных рядов: сглаживание (например, метод скользящего среднего) и декомпозиция временных рядов для выявления трендов и сезонных компонентов;
• Feature Engineering: создание дополнительных признаков, таких как день недели, месяц, сезон, праздники и погодные условия

Для прогнозирования пассажиропотока можно рассмотреть следующие алгоритмы машинного обучения.

Линейная регрессия

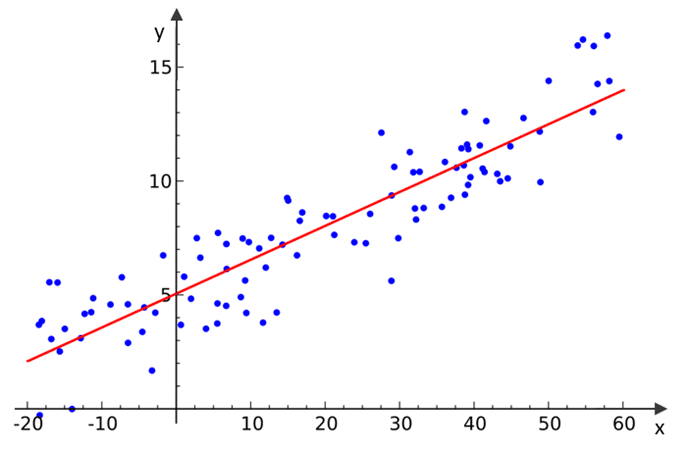
Метод анализа данных, который предсказывает ценность неизвестных данных с помощью другого связанного и известного значения данных. Он математически моделирует неизвестную или зависимую переменную и известную или независимую переменную в виде линейного уравнения (рис. 1). Простая модель, подходящая для базового уровня анализа временных рядов

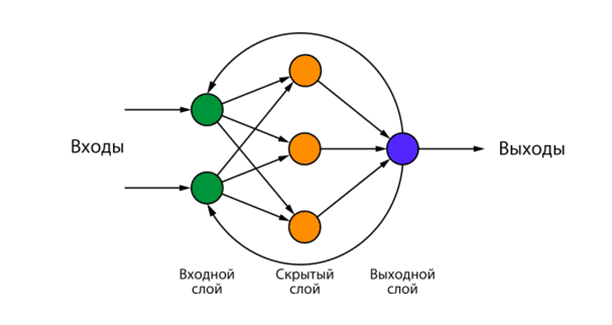
Рекуррентные нейронные сети (RNN)

Сети с циклами, которые хорошо подходят для обработки последовательностей. Обучение RNN (рис. 2) аналогично обучению обычной нейронной сети. Также используется алгоритм обратного распространения, но с небольшим изменением. Поскольку одни и те же параметры используются на всех временных этапах в сети, градиент на каждом выходе зависит не только от расчетов текущего шага, но и от предыдущих временных шагов [2]. Например, чтобы вычислить градиент для четвертого элемента последовательности, нужно было бы «распространить ошибку» на 3 шага и суммировать градиенты. Этот алгоритм называется «алгоритмом обратного распространения ошибки сквозь время». Сети способны учитывать временные зависимости, что делает их полезными для задач прогнозирования временных рядов.

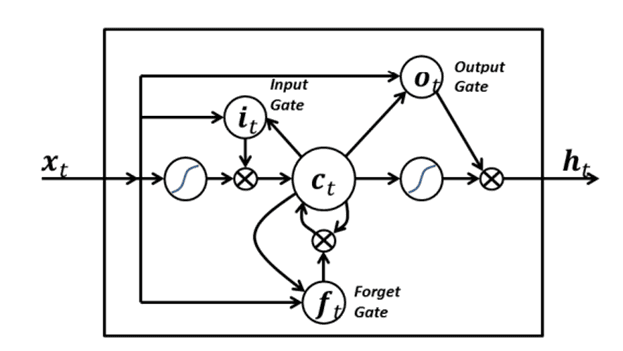
Долговременная краткосрочная память (LSTM)

Рекуррентные нейронные сети добавляют память к искусственным нейронным сетям, но реализуемая память получается короткой — на каждом шаге обучения информация в памяти смешивается с новой и через несколько итераций полностью перезаписывается.

LSTM-модули (рис. 3) разработаны специально, чтобы избежать проблемы долговременной зависимости, запоминая значения как на короткие, так и на длинные промежутки времени. Это объясняется тем, что LSTM-модуль не использует функцию активации внутри своих рекуррентных компонентов. Таким образом, хранимое значение не размывается во времени и градиент не исчезает при использовании метода обратного распространения ошибки во времени при тренировке сети [3].

LSTM-блоки содержат три или четыре «вентиля», которые используются для контроля потоков информации на входах и на выходах памяти данных блоков. Эти вентили реализованы в виде логистической функции для вычисления значения в диапазоне [0; 1]. Умножение на это значение используется для частичного допуска или запрещения потока информации внутрь и наружу памяти. На рисунке 3 x_t – входной вектор – контролирует меру вхождения нового значения в память, c_t – вектор состояний, а h_t – выходной вектор. Ранее упомянутые «вентиля»: f_t – вектор вентиля забывания, i_t – вектор входного вентиля, o_t – вектор выходного вентиля. «Выходной вентиль» контролирует меру того, в какой степени значение, находящееся в памяти, используется при расчёте выходной функции активации для блока.

Резюмируя, это улучшенная версия RNN, способная запоминать долгосрочные зависимости, что особенно важно при прогнозировании на длительные периоды.

Градиентный бустинг (XGBoost, LightGBM)

Градиентный бустинг[4] — это техника машинного обучения для задач классификации и регрессии, которая строит модель предсказания в форме ансамбля слабых предсказывающих моделей, обычно деревьев решений. Обучение ансамбля проводится последовательно. На каждой итерации вычисляются отклонения предсказаний уже обученного ансамбля на обучающей выборке. Следующая модель, которая будет добавлена в ансамбль будет предсказывать эти отклонения. Таким образом, добавив предсказания нового дерева к предсказаниям обученного ансамбля мы можем уменьшить среднее отклонение модели, которое является целью оптимизационной задачи. Новые деревья добавляются в ансамбль до тех пор, пока ошибка уменьшается, либо пока не выполняется одно из правил "ранней остановки".

В основе XGBoost лежит алгоритм градиентного бустинга деревьев решений.

LightGBM - это библиотека, разработанная в Microsoft, которая обеспечивает эффективную реализацию алгоритма повышения градиента. Основным преимуществом LightGBM являются изменения в алгоритме обучения, которые значительно ускоряют процесс и во многих случаях приводят к созданию более эффективной модели.

Для повышения точности предсказаний можно также изучить использование ансамблевых методов, которые подразумевают объединение нескольких моделей:

• Стэкинг (англ. stacking) - комбинирование различных моделей (например, LSTM и XGBoost) для получения итогового прогноза;
• Бэггинг (англ. bagging) - усреднение предсказаний нескольких моделей одного типа для уменьшения вариативности и повышения устойчивости предсказаний

Выбор основного алгоритма для построения модели, будет произведен в результате сравнения результатов тестирования вышеописанных алгоритмов на тестовой выборке данных.

Процесс обучения модели включает следующие этапы:

• Разделение данных - разделение исходного датасета на обучающую и тестовую выборки;
• Валидация модели - использование кросс-валидации для оценки производительности модели и предотвращения переобучения;
• Применение методов поиска гиперпараметров (Grid Search, Random Search) для настройки модели и повышения ее точности.

Адекватность модели можно оценить по нескольким критериям, используя различные метрики: средняя абсолютная ошибка (MAE), среднеквадратичная ошибка (RMSE), коэффициент детерминации (R²) [5].

Средняя абсолютная ошибка измеряет среднее значение абсолютных ошибок между предсказанными значениями и фактическими наблюдаемыми значениями. MAE легко интерпретировать и использовать для понимания средней ошибки модели.

Среднеквадратичная ошибка измеряет средний квадрат разностей между предсказанными и фактическими значениями, а затем извлекает квадратный корень из этого значения. RMSE более чувствительна к большим ошибкам, так как квадрат разности увеличивает вес больших ошибок. Это делает RMSE полезной, когда необходимо уделить больше внимания большим отклонениям.

Коэффициент детерминации (R²) измеряет долю дисперсии зависимой переменной, которая объясняется независимыми переменными модели. R² показывает, насколько хорошо предсказанные значения совпадают с фактическими.

Использование комбинации MAE, RMSE и R² обеспечивает всестороннюю оценку модели. MAE даст понимание средней ошибки, RMSE подчеркнет значимость крупных ошибок, а R² покажет степень объясненности вариации данных.

После оценки модели следует проанализировать ошибки.

Выявление систематических ошибок поможет понять, где модель допускает наибольшие отклонения, и внести соответствующие корректировки.

Исследование распределения остатков (разница между фактическими значениями и предсказаниями) может выявить паттерны, которые модель не учла. Если остатки не распределены случайным образом, это указывает на необходимость улучшения модели.

Анализ важности признаков поможет определить, какие признаки оказывают наибольшее влияние на предсказания модели. Это можно сделать с помощью таких методов, как SHAP values или Feature Importance из ансамблевых моделей.

После успешного тестирования и оценки модель можно интегрировать в систему управления городским транспортом. Это позволит автоматически прогнозировать пассажиропоток и корректировать расписания в реальном времени.

Выводы

Разработка модели прогнозирования пассажиропотока имеет большое практическое значение.

Использование различных методов машинного обучения, включая рекуррентные нейронные сети (RNN) и градиентный бустинг (XGBoost), позволит достичь высокого уровня точности предсказаний. Сравнение различных методов построения модели позволит точно оценить их производительность конкретно в этой задаче, а это обеспечит объективный выбор наиболее эффективного алгоритма для конкретных условий городской транспортной системы.

Модель позволит более точно прогнозировать пассажиропоток, что поспособствует оптимизации маршрутов и расписания общественного транспорта. Это улучшит использование ресурсов и снижает затраты.

Предсказания пассажиропотока позволяют транспортным компаниям лучше реагировать на изменения в спросе, предоставляя пассажирам более удобные и надежные услуги.

Для поддержания высокой точности прогнозов рекомендуется регулярно обновлять данные и переобучать модель. Это позволит учитывать изменения в паттернах пассажиропотока и внешних факторах.

Постоянный мониторинг производительности модели и сравнение предсказаний с фактическими данными позволит своевременно выявлять отклонения и корректировать модель. Важно также анализировать ошибки и остатки для дальнейшего улучшения модели.

Включение дополнительных данных, таких как информация о дорожной обстановке, изменениях в инфраструктуре и социально-экономических факторах, может повысить точность модели и сделать прогнозы более релевантными.

Список использованной литературы

1. Воронина В.В, Теория и практика машинного обучения / В.В, Воронина, А.В. Михеев. – Ульяновск : УлГТУ, 2017. – 13-106 с. URL: https://lib.laop.ulstu.ru/venec/disk/2017/191.pdf.
2. Рекуррентные нейронные сети // Викиконспекты URL: https://neerc.ifmo.ru/wiki/index.php?title=Рекуррентные_нейронные_сети.
3. Долгая краткосрочная память // Викиконспекты URL: https://neerc.ifmo.ru/wiki/index.php?title=Долгая_краткосрочная_память.
4. XGBoost // Викиконспекты URL: https://neerc.ifmo.ru/wiki/index.php?title=XGBoost.
5. Python и машинное обучение. Машинное и глубокое обучение с использованием Python, scikit-learn и TensorFlow / Себастьян Рашка, Вахид Мирджалили. – Россия : Диалектика, 2019. – 656 с URL: https://djvu.online/file/rsawp3kW55xzy.