Геологистические методы оптимизации местоположения транспортно-логистических центров

Аннотация

Бутыркин А.Я., Филиппов М.М. Геологистические методы оптимизации местоположения транспортно-логистических центров Рассмотрены системы блочного моделирования. Исследовано моделирование уравнения гармонического осциллятора. Проведено сравнение моделирующих сред.Удовлетворение потребностей населения качественными услугами, предоставляемыми транспортным комплексом, возможно за счет формирования технически, технологически и экономически сбалансированного транспортного комплекса с применением новых методик и инструментов оптимизации транспортной системы. Целью данной статьи является анализ проблем и перспектив организации работы транспортной системы в условиях внедрения современных геоинформационных технологий и определение усовершенствования наиболее значимых направлений при организации перевозочного процесса являются. Авторы приходят к выводу, что внедрение геологистических методов, интеллектуальная аналитика, ситуационное моделирование позволят оптимизировать выбор местоположения транспортно-логистических центров, минимизировать транспортные затраты, соответственно, повысить эффективность взаимодействия участников перевозочного процесса и логистических услуг регионов.

Введение

Определяющим фактором размещения промышленности являются затраты на транспортировку продукции, минимизация этих затрат. Поэтому производство размещается в местах сосредоточения сырья, у потребителя готовой продукции или где-то между ними (это касается главным образом перерабатывающей промышленности) [Паленая, 2021].

Для геологистических исследований очень важны гравитационные модели, поскольку они учитывают не только расстояние перевозок, но и такой фактор территориальных связей, как влияние крупных городов, что позволяет прогнозировать возможные и оптимизировать существующие транспортно-логистические центры (ТЛЦ) между ними.

Основная часть

Впервые гравитационная модель была предложена в середине XIX века американцем Г. Кэри, который отметил, что большие города имеют большую силу притяжения, чем меньшие, а значит, между ними возникают большие ТЛЦ. Это позволило У.Рейлив в 1931 году создать модель торговой гравитации, суть которой состоит в том, что большие города привлекают большее количество покупателей, готовых преодолевать дальние расстояния до крупных торговых центров, а сила притяжения пропорциональна количеству населения или обороту местной торговли [Alen, Skender, Zaninovic, 2019].

Популярной в географии транспорта является концепция конвергенции пространства-времени, которая заключается в процессе увеличения объема пространства, который можно преодолеть за аналогичное количество времени в результате повышения скорости, уменьшения транспортных расходов, роста транспортной доступности. Логистика придает этой концепции несколько иной смысл, учитывая организацию и синхронизацию потоков через узловые и сетевые стратегии, а также включая в эту концепцию понятие времени как управленческого ограничения перевозок [Hesse, 2004].

Среди логистических парадигм – аналитической, технологической, маркетинговой и интегральной – последняя наиболее полно соответствует сущности и цели геологистики, поскольку предполагает межотраслевую и пространственно-территориальную увязку хозяйственных объектов (участников логистических отношений) [Lisyuk, 2019].

Понятие геологистики,в отличие от понятия логистики, пока недостаточно разработано как в нашей стране, так и на Западе. Большинство авторов относят геологистику к логистическим концепциям третьего поколения (начало XXI века), определяя ее как теорию и практику территориально-экологической оптимизации логистических систем разных масштабов: микро- (предприятие), мезо- (область), макро- (страна), мега- (группа стран), мета- (мир) уровней путем сбыта продукции [Виноградова, 2002].

Профессор С.В. Носков применяет понятие «общественно-географическая логистика» (geologistics). По его мнению, общественно-географическая логистика – это новейшее междисциплинарное научно-практическое направление, формируемое на грани логистики и общественной географии, исследующее научную организацию (в современном логистическом понимании) территориально-экономических (или шире – географо-пространственных) связей. «Формула» общественно-географической логистики, по мнению ученого, это: территориальные аспекты логистики + экологистика + геоинформационные системы в логистике. Именно территориальная и экологическая направленность отличают геологистику от логистики. Второе отличие – комплексный подход к решению логистических проблем, нашедший отражение в особенностях геологистических операций. Наконец, третье отличие – использование методов пространственного, в частности топологического, анализа логистических сетей и территориальных моделей логистических систем, теорий многостадийных систем производства [Носков, 2001].

По мнению ученой И.П. Черной, геологистика – это новейшее направление в логистике, которое заключается в формировании и распределении мировых транспортных потоков, а также отслеживании их в реальном режиме времени с применением современных сервисов с целью нахождения оптимальных решений, обеспечивая объединение процессов функциональных структур предприятий в единую систему [Черная, 2013]. В работе [Кочетов, 2016] геологистику предлагается рассматривать как научное направление, бизнес-направление и функцию хозяйственного управления. Как научное направление, геологистика – это учение об эффективной пространственно-территориальной организации и управлении логистическими системами микро-, мезо-, макро-, мега- и метауровней. Как бизнес направление, геологистика – это совокупность транспортно-экспедиторско-складских операций с целью изготовления и доставки товара определенного вида и качества в определенном количестве определенному потребителю в определенное место и время с минимальными затратами. Как функцию хозяйственного управления ее определяют как форму управления физическим распределением товара во времени и пространстве. В свою очередь, логистику с позиции менеджмента интерпретируют как компанию управления целенаправленной подготовкой и целесообразным внедрением средств и услуг, нужных для решения конкретных задач [Кочетов, 2001].

Еще один оригинальный подход к определению геологистики связан со знаниями об использовании мировых ресурсов для обеспечения благосостояния человечества. Выделяют три основных этапа геологистики:

1. идентификация ресурсов;
2. инвентаризация ресурсов;
3. приведение ресурсов в движение для достижения целей человека [Sachaklian, 2012].

Можно заключить, что понятийно-терминологический аппарат (ПТА) геологистики в полной мере не сформирован. Термины, которыми оперирует геологистика, в основном заимствованы из логистики и географии транспорта.

Мы определяем геологистику как новое междисциплинарное научно-практическое направление, исследующее общественно-географические предпосылки и геопространственную организацию территориальных логистических систем, создаваемых ими пассажирских, грузовых, информационных и финансовых потоков для выбора оптимального вида транспорта, оптимальных маршрутов перевозок, оптимальных логистических каналов и оптимального местоположения транспортно-логистических центров.

По мнению профессора Э.Г. Кочетова, ядром геологистики является понятие территориально-логистической проблемы и создание территориальной сети современных логистических коммуникаций, что предусматривает аспекты (территориально-отраслевой, территориально-организационный, территориально-функциональный) и пути решения транспортно-логистических задач по созданию оптимальной транспортно-логистической инфраструктуры.

Геологистика учитывает различие терминов «пространство» и «территория», трактуя «пространство» как географически абстрактное понятие, а «территорию» – как географически конкретное, для которого характерно определенное местоположение и конфигурация. Отсюдапонятие «пространственные связи и взаимоотношения» имеет более общий характер и относится ко всей пространственно-территориальной совокупности логистических проблем, а «территориальные связи» – к логистической проблеме региона.

Центральным понятием и в логистике, и в геологистике является логистическая система, а в контексте нашего исследования ключевым понятием является региональная логистическая система (РЛС). Относительно понимания РЛС сложилось несколько смежных подходов. Один из них определяет РЛС как территориальную организацию сферы обращения, где происходит согласование интересов производителей и потребителей. Это позволяет совместить усилия различных единиц, производящих товары и услуги, с целью оптимизации финансовых, материальных и трудовых ресурсов, используемых регионом для реализации своих социально-экономических задач [Шишко, 2020].

Мы считаем, что содержание РЛС следует определять как форму территориальной организации логистической деятельности в пределах региона, основными элементами которой являются взаимосвязанная сеть транспортно-логистических центров разного иерархического уровня, многокомпонентная обслуживающая инфраструктура и централизованная система управления [Жильцова и др., 2022].

В исследовании территориальных логистических сетей (ТЛС) применимы общенаучные и конкретно научные методы [Азимов, 2018], а также философские принципы движения, развития, взаимосвязи, историзма и т.д. Из общенаучных методов чаще всего используют математические (теория графов, задачи линейного программирования) и статистические методы, а также географическую информационную систему (ГИС).

В системе методов общественно-географического прогнозирования регионального развития теория графов доминирует, являясь одним из методов анализа пространственного взаимодействия [Zhiheng Zhao et al., 2022]. Топологический анализ ТЛС на основе теории графов позволяет решить такие основные проблемы, как определение рационального размещения РЛЦ и расчет оптимальных маршрутов движения. Эту проблему решают с помощью показателей центральности и оценки местоположения РЛЦ в отношении главных путей. Такой подход помогает определить оптимальные пункты размещения РЛЦ [Batty, 2022].

Выбор оптимального местоположения РЛЦ считаем целесообразным определять путем методов центрографии и минимума суммарных расстояний. Постановка задачи оптимального размещения РЛЦ на базе центрографического анализа формулируется так. Пусть на исследуемой территории находятся M производителей/потребителей определенной продукции, координаты которых (xi,yi),i = 1,…, M. Обозначим через pi,i = 1,…, M значение некоторого абсолютного показателя, характеризующего объем производства/потребления этой продукции. Ставится задача определить координаты (X,Y) распределительного РЛЦ, для которого взвешенная сумма квадратов расстояний до производителей/потребителей минимальна. Рассмотрим задачу по логическим блокам.

Переменными оптимизации являются координаты X,Y. Квадрат расстояния от распределительного центра до i-го производителя/потребителя вычислим по формуле Евклидового расстояния. Тогда взвешенную сумму квадратов расстояний M можно записать так: S (X,Y) = pi [(xi-X)2+(yi-Y)2]. Критерием оптимизации является минимизация этой функции. Блок ограничений по этой задаче отсутствует. В некоторых регионах очень неправильной формы он может присутствовать, если необходимо гарантировать принадлежность найденного центра к территории региона. Решением такой задачи являются координаты центра притяжения изучаемого показателя, которые можно вычислить по формулам центрографического анализа:

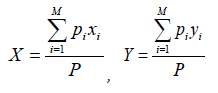
где, P – суммарное значение абсолютного показателя.

Критерием оптимизации является минимизация функции S(X,Y). Блок ограничений по этой задаче отсутствует.

Посредством теории графов, а именно задач о минимальных расстояниях, обеспечивается решение еще одной важной проблемы – определение оптимальных маршрутов движения в РЛС. В частности, используются задачи о минимальном сообщении, о кратчайшем пути и о дереве кратчайших расстояний [Тихомирова, 2010].

Рассмотрим оптимизационную задачу построения малого дерева на графе [Wu Xiaolan, Murray, 2008]. Задан неориентированный граф с известными расстояниями между узлами, то есть длинами ребер. Нужно выделить в нем дерево, имеющее минимальную суммарную длину ребер. Такая задача имеет очевидную практическую ценность, потому что фактически позволяет спроектировать самую короткую коммуникационную сеть между заданным множеством узлов.

Пусть n – количество узлов заданного графа, djl – заданные расстояния между узлами с номерами j и l:j,l1,2,...,n. Переменными оптимизации считаем величины xjl, которые могут иметь значение 0 или 1, причем xjl= 0, если в выделенном дереве узлы с номерами j и l не соединены ребром, иx jl=1,если в оптимальном дереве существует ребро между узлами j и l. В принятых обозначениях очевидно, что суммарную длину ребер выделенного в графе дерева можно вычислить как:

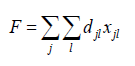
Поэтому критерием оптимальности является минимизация именно так вычисленной функции F. Блок ограничений по этой задаче включает три подблока. Первый напоминает, что величины xjl могут принимать значения только 0 или 1. Второй фиксирует тот факт, что в графе-дереве количество ребер всегда на единицу меньше, чем количество узлов. Третий – обеспечивает, чтобы в полученном графе не было изолированных узлов. Этого можно достичь, если потребовать строгой положительности суммы.

Приоритет в общественно-географическом анализе ТЛС имеет метод разложения на элементарные компоненты. Этот метод включает две составляющие – выделение «полярных» сетей (состоит в разделении ТЛС на элементарные компоненты на основании алгоритма кратчайшего пути и дает возможность определения оптимальных зон действия РЛЦ) и классификацию трасс (позволяет выделить главные коммуникации ТЛС, требующие особого внимания, и второстепенные).

Теория графов применима и для пространственного анализа взаимодействия составных элементов ТЛС. При этом множество отношений означает множество территориально- логистических потоков, связывающих элементы системы между собой. Их характеризуют отношение эквивалентности, транзитивности, рефлексивности, симметричности, предшествования или следования. Эти виды отношений можно выразить в форме графов и таким образом найти методы оптимизации внутрипроизводственных территориальных связей и структур. Графы используются и в качестве графических отображений классификаций. В этом качестве они находят практическое использование, в частности, в разработке метода «ветвей и границ», с помощью которого можно решить классическую задачу сбытовой логистики – задачу коммивояжера [Ульянов, 2022].

В исследованиях РЛЦ широко применяется метод линейного программирования (транспортная задача). Отметим, что линейное программирование – один из алгоритмов решения известной задачи о максимальном потоке транспортной сети [Schrijver, 2003]. В системе методов общественного географического прогнозирования регионального развития линейное программирование относится к группе методов оптимизации развития регионов [Шаяхметова, Омарова, Дрозд, 2020]. Постановка транспортной задачи предполагает, что территориальный комплекс включает в себя m производителей определенной продукции n ее потребителей. Сделаем ряд обозначений:

• ai – годовой объем производства продукции i-м производителем;
• bj – годовой объем потребления продукции j–м потребителем;
• cij – стоимость перевозки единицы продукции от i-го производителя к j-му потребителю.

Переменными оптимизации являются xij – годовые объемы перевозок от i-го производителя до j-го потребителя. Таких переменных есть m?n. Общая стоимость всех перевозок от производителей к потребителям является:

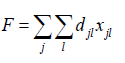
Интересы регионального уровня заключаются в том, чтобы достичь максимальной экономии на перевозках.

Важным представляется метод применения теории информации и энтропии. Информация и энтропия находятся в обратном соотношении: чем больше информации, тем меньше энтропия, и наоборот. Энтропией в науке обозначают неопределенность. Для свойства уровня энтропии определенного явления употребляют энтропийные меры: концентрации, размещения, дифференциации, трудности сети, пространственного соответствия. Их вычисляют на основе формулы Шеннона:

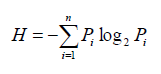
где, Pi – вероятность.

Кроме того, в зарубежной практике широко используются многофункциональные средства ГИС-пакетов. Главные направления их применения таковы [He Handong, Liu Yanrong, Cui, Jing, Hu Di, 2022]: моделирование ТЛС, отражение субъектов геологистики, анализ современной геологистической ситуации, планирование геологистических операций. Конкретно научным считается метод территориально-логистического инжиниринга (ТЛИ). Его суть заключается в объединении процессов поставок, производства и сбыта в сквозной логистический (товарно- информационно-финансовый) поток и его оптимизации на основании классического логистического принципа «точно в срок». Метод ТЛИ включает следующие компоненты [Кочетов, 2001]:

• согласование параметров логистического потока на участках снабжения, производства, сбыта, причем исходными/определяющими параметрами должны быть параметры потребления/сбыта – объем/количество и состояние/качество товара, место и время его сбыта;
• территориальная оптимизация логистического потока на участках снабжения, производства, сбыта с целью минимизации логистических затрат, каждый участок имеет свои территориальные особенности, соответственно, свои методы оптимизации;
• временная синхронизация, то есть определение необходимой скорости логистического потока для каждого функционального участка (снабжение, производство, сбыт);
• экологическая оптимизация логистического потока, включающая как определение экологических проблем (связанных с транспортной составляющей) и их влияния на природную среду и устойчивое развитие региона и страны, так и разработку и осуществление соответствующих мер по улучшению экологических показателей.

На метауровне ценными являются данные индекса логистической эффективности (Logistics Performance Index(LPI)), который рассчитывается для каждой страны один раз в два года на основе информации, полученной с помощью анкет более чем 800 крупнейших мировых логистических компаний. Оценка логистической активности страны осуществляется на основе комплекса показателей – таможенный контроль, инфраструктура, процессы обслуживания, сроки выполнения заказов, объемы международных перевозок, возможности выявления и отслеживания [Logistics Performance Index 2022, www].

Заключение

На основе проведенного исследования можно сделать вывод о том, что внедрение геологистических методов, интеллектуальная аналитика, ситуационное моделирование позволят оптимизировать выбор местоположения транспортно-логистических центров, минимизировать транспортные затраты, соответственно, повысить эффективность взаимодействия участников перевозочного процесса и логистических услуг регионов.

Библиография

1. Азимов П.Х. Управление эффективностью транспортно-логистической системы: методологичекие принципы // Вестник Марийского государственного университета. Серия: Сельскохозяйственные науки. Экономические науки. 2018. Т. 4. № 2(14). С. 97-105.
2. Виноградова М.Ю. Формирование трансакционных издержек в логистике хозяйственных связей: дисс. канд. экон. наук. СПб., 2002. 183 с.
3. Жильцова О.Н. и др. Маркетинг территорий. 1-е изд. М.: Юрайт, 2022. 262 с.
4. Кочетов Э.Г. Геоэкономика. Энциклопедия. М., 2016. 599 с.
5. Кочетов Э.Г. Глобалистика как геоэкономика, как реальность, как мироздание = Globalistics: geoeconomics, reality, the universe: Новый ренессанс - истоки и принципы его построения, фундамент. опоры, теорет. и методол. каркас. М.: Прогресс, 2001. 703 с.
6. Носков С.В. Оптимальное управление потоковыми процессами в региональной экономике: автореф. дис. д-ра экон. наук. Самара, 2001. 40 с.
7. Паленая А.А. Формирование логистических систем при форматировании рыночных условий // Экономика: вчера, сегодня, завтра. 2021. Т. 11. № 2-1. С. 26-35.
8. Тихомирова А.Н., Сидоренко Е.В. Математические модели и методы в логистике. М.: НИЯУ МИФИ, 2010. 318 с.
9. Ульянов М.В. Комбинированный точный алгоритм решения задачи коммивояжера // Задачи транспортной логистики. Информационные технологии. 2022. Т. 28. № 3. С. 141-147.
10. Черная И.П. Геоэкономика. М.: Дашков и К°, 2013. 247 с.
11. Шаяхметова Б.К., Омарова Ш.Е., Дрозд В.Г. Организация системы транспортной логистики в регионах РК на базе решения задачи коммивояжера // Форум. Серия: Гуманитарные и экономические науки. 2020. № 3 (20). С. 85-92.
12. Шишко ЕЛ. Региональная логистическая система: управление, оценка рисков // Материалы XV Международной научно-практической конференции «Логистика – евразийский мост». Красноярск-Енисейск: Красноярский государственный аграрный университет, 2020. С. 220-223.
13. Костюков В.Е., Жигалов В.И., Кибкало А.А., Батурин В.П. Ц ифровой подводный добычной // комплекс // Нефть. Газ. Новации. 2018. № 12. С. 21-23.
14. Огородников А.Ю., Чурин В.В. Аксиологические основания рисков социального участия в условиях глобализации// Информационное общество. 2016. № 6. С. 19-24.
15. Огородников А.Ю. Становление инновационного потенциала руководителей в системе образования // Инновационные проекты и программы в образовании. 2015. № 4. С. 28-34.
16. Махиборода М.Н. Нормативно-правовое регулирование внеуличного транспорта: гражданско-правовой аспект // Евразийский юридический журнал. 2021. № 9 (160). С. 188-190.
17. Берзон Н.И., Лысенок Н.И. ОЦЕНКА ИНВЕСТИЦИОННОЙ ПРИВЛЕКАТЕЛЬНОСТИ ФОНДОВЫХ РЫНКОВ СТРАН БРИКС Финансы и бизнес. 2021. Т. 17. № 4. С. 18-31.
18. Лысенок Н.И. ПОТЕНЦИАЛ ВОССТАНОВЛЕНИЯ ЭКОНОМИК СТРАН БРИКС В ПОСТПАНДЕМИЧЕСКОМ МИРЕ В сборнике: Архитектура финансов: вызовы новой реальности. Сборник материалов XI Международной научно-практической конференции. Под научной редакцией И.А. Максимцева, Е.А. Горбашко, В.Г. Шубаевой. Санкт-Петербург, 2021. С. 494-496.
19. Chargazia T.Z., Popova I.V. Informational support of the investment process in a large city economy // Economy of Regions. 2016. Т. 12. № 4. С. 1061-1068.
20. Alen H., Skender P.H., Zaninovic P.A. Trade Logistics -the Gravity Model Approach. Zbornik Radova Ekonomskog Fakulteta u Rijeci // Proceedings of Rijeka School of Economics. 2019. No. 37. P. 327-342.
21. Batty M. Integrating space syntax with spatial interaction// Urban Informatics. 2022. No. 1.
22. He Handong, Liu Yanrong, Cui, Jing, Hu Di. Scenario Expression Method for Regional Geological Structures // ISPRS International Journal of Geo-Information. 2022. No. 11(47).
23. Hesse M. The transport geography of logistics and freight distribution // Journal of Transport Geography. Amsterdam: Elsevier B. V. 2004. 14 p.
24. Lisyuk V. Theory of market logistics development in spatial and timeline dimension// Economic innovations. 2019. No. 21. P. 113-124.
25. Logistics Performance Index 2022. URL: http://chartsbin.com/view/41356
26. Sachaklian H.A. Geopolitics versus Geologistics // Air & Space Power Journal. Montgomery: Air University, 2012. P. 132-145.
27. Schrijver A. Combinatorial optimization. Berlin, Heidelberg, New York: Springer-Verlag, 2003. Vol. A. 1881 p.
28. Wu Xiaolan, Murray A. A New Approach to Quantifying Spatial Contiguity Using Graph Theory and Spatial Interaction // International Journal of Geographical Information Science. 2008. No. 22. P. 387-407.
29. Zhiheng Zhao et al. Digital Twin-enabled Dynamic Spatial-temporal Knowledge Graph for Production Logistics Resource Allocation // Computers & Industrial Engineering. 2022. No. 171.