Способ измерения True RMS переменного напряжения с помощью микроконтроллера
Автор: Кузнецов Д.Н., Захарченко И.А.
Источник: Автоматизация технологических объектов и процессов. Поиск молодых : сборник научных трудов ХХIII международной научно-технической конференции аспирантов и студентов в г. Донецке 23-25 мая 2023 г. - Донецк : ДОННТУ, 2023. – С. 121-124.
Аннотация.
Кузнецов Д.Н., Захарченко И.А. - Способ измерения True RMS переменного напряжения с помощью микроконтроллера
В работе иследован метод вычисления True RMS переменного напряжения.
Понятие истинного среднеквадратичного значения (TrueRMS)
Точные измерения - трудная задача, стоящая перед технологами и специалистами по обслуживанию современных производств и оборудования различных организаций. В нашу повседневную жизнь все больше и больше входят персональные компьютеры, приводы с регулируемой скоростью и другое оборудование, имеющее несинусоидальные характеристики потребляемого тока и рабочего напряжения (в виде кратковременных импульсов, с искажениями и т.п.). Такое оборудование может вызвать неадекватные показания обычных измерителей с усреднением показаний (вычисляющих среднеквадратическое значение).
RMS означает среднеквадратичное значение, а TRMS (True RMS) - истинное среднеквадратичное значение. Инструменты TRMS намного более точны, чем RMS при измерении переменного напряжения и тока. Поэтому все профессиональные мультиметры имеют возможности измерения True RMS.
Самый распространенный способ измерения такого среднеквадратического значения напряжения при помощи измерительного прибора заключается в выпрямлении переменного тока, определении среднего значения выпрямленного сигнала и умножении результата на коэффициент 1,1 (соотношение между средним и среднеквадратическим значениями идеальной синусоиды). Однако, при отклонении синусоидальной кривой от идеальной формы данный коэффициент перестает действовать. По этой причине измерители с усреднением показаний зачастую дают неверные результаты при измерении токов в современных силовых сетях.
Таким образом, RMS измерения нельзя считать надежными, потому что в любой установке в реальных условиях имеется множество источников шума, из-за которых форма волны переменного напряжения никогда не бывает идеальной, что приводит к большим погрешностям измерений.
При измерении True RMS используется более сложный математический аппарат определения реального эффективного значения переменного напряжения, не зависимо от формы его кривой, что позволяет приблизить значение к реальности и существенно повысить точность измерений.
Целью работы является исследование простого и максимально дешевого способа измерения True RMS переменного напряжения с использованием 8-разрядного микроконтроллера.
Простой метод измерений TrueRMS
Измерение True RMS переменного напряжения - задача не совсем простая [1]. Как известно действующее значение переменного напряжения определяется выражением
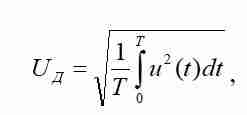
При аппаратной реализации для вычисления подинтегрального выражения необходимо проквантовать сигнал с некоторой частотой, заведомо превосходящей не менее чем в 10 раз частоту квазисинусоиды.
Также необходимо учесть, что все стандартные микроконтроллеры имеют однополярное питание. Поэтому измерить мгновенное переменное напряжение в момент отрицательной полуволны не представляется возможным.
В работе [2] предложено простое решение, как внести постоянную составляющую в сигнал. Вместе с тем в том решении определение момента, когда стоит начать или закончить процесс вычисления True RMS представляется довольно громоздким.
В данной работе предлагается метод преодоления этого недостатка, а также вычисление интеграла с большей точностью, что позволяет снизить программно-аппаратные затраты на реализацию данного способа до минимума.
Рассмотрим структурную схему процесса вычисления True RMS, представленную на рисунке 1 [3]. Данная схема обеспечивает преобразование среднеквадратичного значения переменного напряжения произвольной формы в постоянное напряжение.
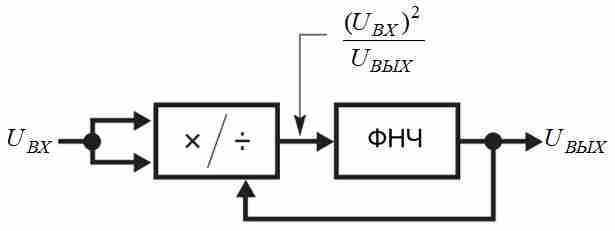
В первом блоке выполняется операция возведения входного сигнала UВХ в квадрат с последующим делением на выходной сигнал UВЫХ. Полученный результат пропускается через фильтр низких частот (ФНЧ), который выделяет постоянную составляющую и формирует выходной сигнал преобразователя, равный True RMS входного сигнала. Рассмотрим математический аппарат,
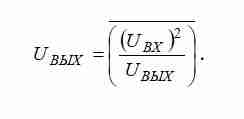
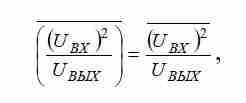
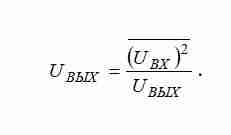
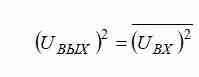
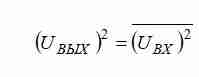
Проверка теории путем имитационного моделирования
С целью проверки предложенного метода вычисления True RMS переменного напряжения выполним моделирование структурной схемы в программе Proteus ISIS (см.рисунок 2).
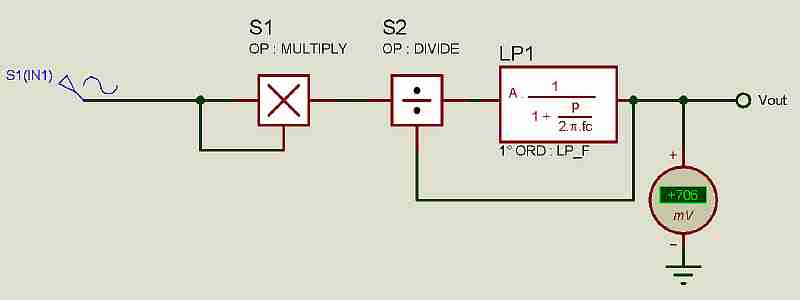
Модель содержит блок умножения аналоговых сигналов S1, блок деления аналоговых сигналов S2 и фильтр низких частот первого порядка LP1 с частотой среза 1 Гц. В результате моделирования при подаче на вход схемы синусоидального напряжения амплитудой 1 вольт и частотой 50 Гц на выходе получено напряжение постоянного тока 0,706 В, что в точности соответствует расчетному значению.
Реализация измерителя True RMS с фильтром «Бегущее среднее»
На рисунке 3 приведена модель принципиальной схемы измерителя True RMS переменного напряжения, выполненная на базе 8-разрядного микроконтроллера ATmega328.
На элементах R1, R2 и С1 собрана схема смещения измерительного сигнала ровно на половину напряжения питания микроконтроллера VCC. Это же напряжение подано на вход AVCC и является опорным для встроенного 10-разрядного аналогоцифрового преобразователя АЦП. Для визуализации результатов работы используется виртуальный терминал, подключенный к выходу СОМ-порта микроконтроллера TxD.

На рисунке 4 приведен алгоритм программной реализации рассмотренного выше алгоритма работы микроконтроллера, реализующего принцип преобразования True RMS в постоянный сигнал.
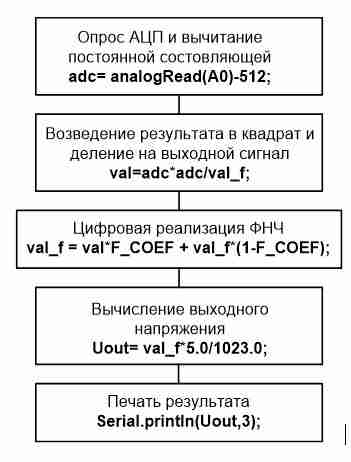
Частота дискретизации при моделировании была принята равной FC=500 Гц, коэффициент фильтра F_COEF=0,002.
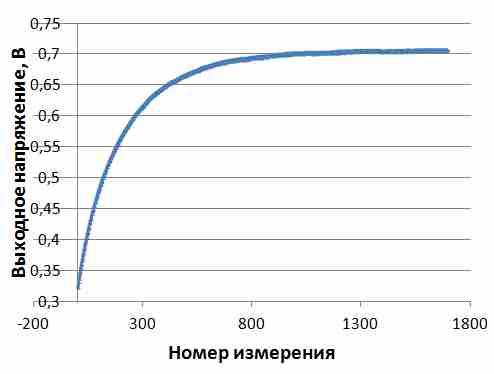
В результате моделирования получили кривую изменения выходного напряжения схемы при подаче на вход синусоидального напряжения амплитудой 1 В с частотой 50 Гц (см.рисунок 5). Из результатов следует, что переходной процесс установления результатов измерений длиться порядка 3 секунд. После чего среднее значение выходного напряжения равно 0,706 В, а уровень пульсаций не превышает 1 мВ.
Для уменьшения длительности переходного процесса можно увеличить коэффициент фильтра F_COEF, при этом, однако, возрастет уровень пульсаций выходного напряжения.
Проектирование цифрового БИХ-фильтра
Недостатком простого фильтра типа «Бегущее среднее», реализованного в предыдущем параграфе является его малое быстродействие. С целью увеличения быстродействия выполним проектирование эффективного цифрового ФНЧ.
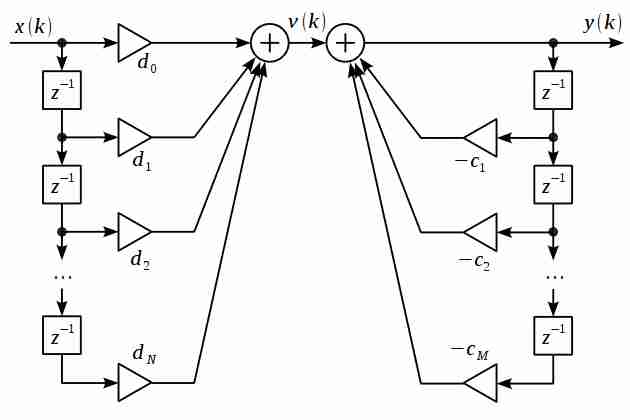
Все цифровые фильтры делятся на две категории: фильтры с конечной импульсной характеристикой (КИХ-фильтры) и фильтры с бесконечной импульсной характеристикой (БИХ-фильтры). В работе будем исследовать БИХ-фильтр, так как при равных вычислительных затратах реализацию фильтров БИХ-фильтр будет обладать лучшими частотными характеристиками. На рисунке 5 представлена структурная схема БИХ-фильтра с прямой формой реализации, выбранная для исследований.
Зададимся исходными данными для расчета цифрового фильтра нижних частот:
- частота дискретизации Fs, Гц 500;
- частота среза Fpass, Гц 5;
- нижняя частота полосы подавления Fstop, Гц 50;
- подавление в полосе заграждения, дБ 40;
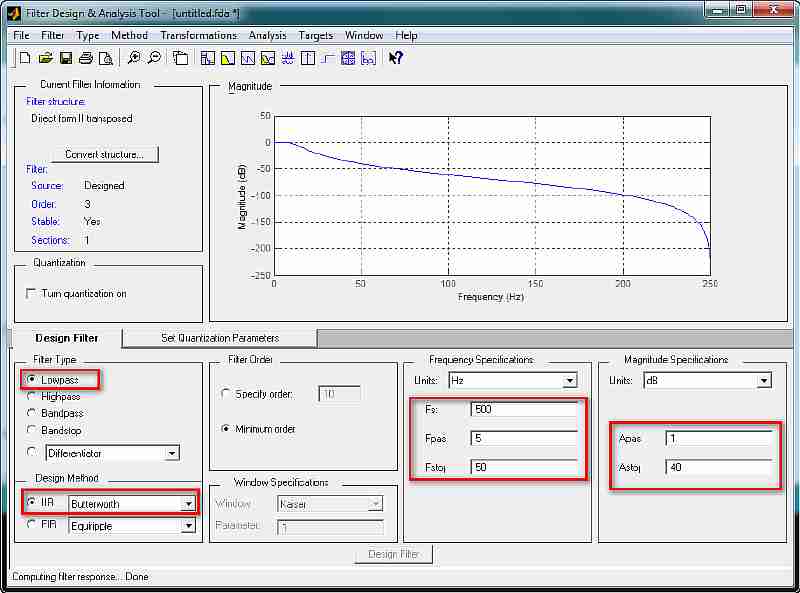
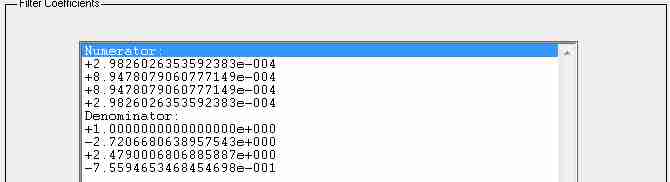
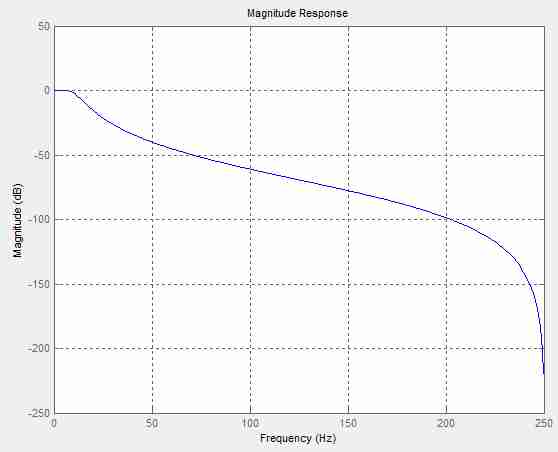
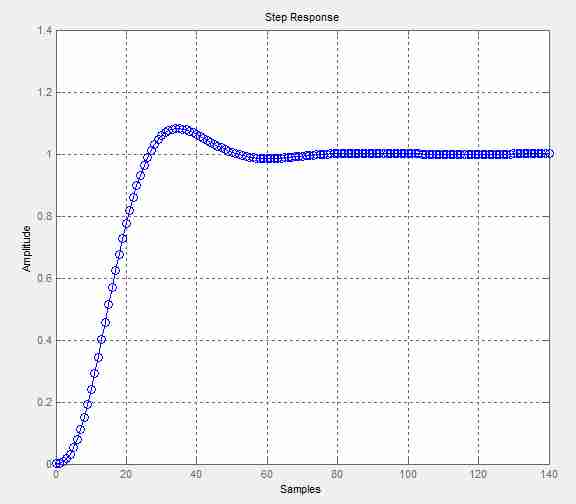
Расчет коэффициентов цифрового фильтра выполним в программе «Filter Design & Analysis Tool (FDAToll)», входящей в пакет MatLab (см.рисунок 7). Полученные массивы коэффициентов фильтра представлены на рисунке 8 Результаты расчета амплитудно-частотной и переходной характеристики БИХ-фильтра нижних частот 3-го порядка приведены на рисунках 9 и 10. соответственно.
В приложении А приведен листинг программы на языке Си, реализующий алгоритм вычислений разработанного БИХ ФНЧ.
Сборка макета и натурные испытания, измерителя true rms
Структурная схема и фото собранного макета для выполнения натурных испытаний разработанного измерителя True RMS переменного напряжения приведены на рисунках 11 и 12 соответственно.
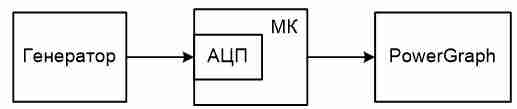

В качестве источника сигнала использовался генератор с размахом синусоидального сигнала 2 В и частотой 50 Гц. В результате получили действующее значение 0.693 В. Пульсации не превышали 1 мВ. Относительная погрешность измерений составила 0,6%, что является приемлемым.
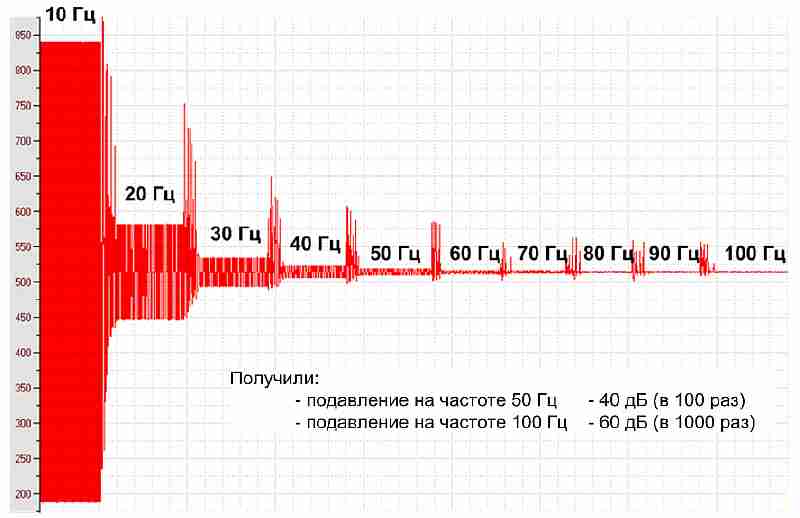
На рисунке 13 приведены результаты исследований амплитудно-частотной характеристики спроектированного БИХ фильтра. С генератора подаем синусоиду амплитудой 1 В и смешенную на 2,5 В на половину диапазона АЦП. Устанавливаем разные частоты от 10 до 100 Гц. Видно, что с ростом частоты коэффициент подавления фильтра растет. Путем трассировки было определено, что действительно подавление на частоте 50 Гц составляет 40дБ (в 100раз). Таким образом, результаты экспериментальных исследований подтвердили результаты теоретических расчетов.
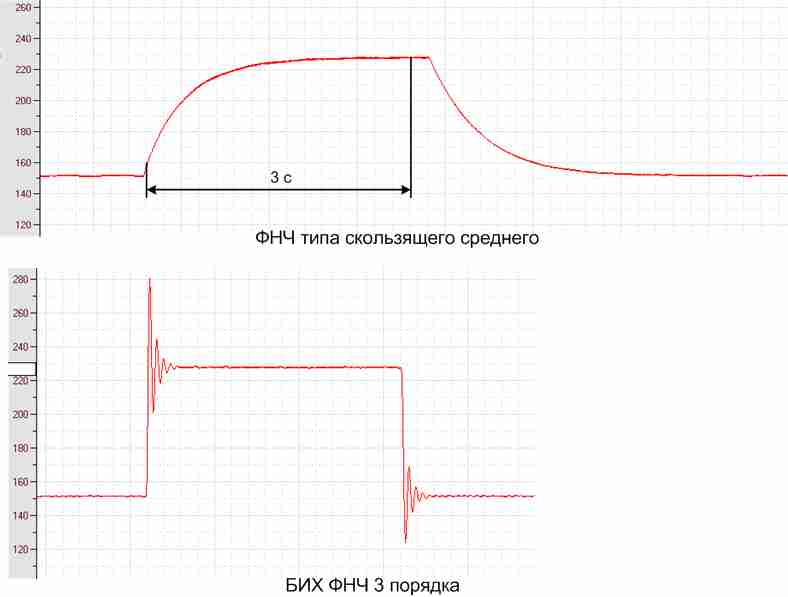
На рисунке 14 приведены результаты исследований переходных характеристик измерителя True RMS для двух типов фильтров:
- ФНЧ «Скользящее среднее».
- Цифровой БИХ ФНЧ третьего порядка.
Из результатов следует, что использование более эффективного цифрового БИХ фильтра позволяет на порядок увеличить быстродействие измерителя True RMS.
Выводы
- Предложенный способ измерения истинного среднеквадратичного значения переменного напряжения (True RMS) на базе 8-разрядного микроконтроллера позволяет сократить до минимума число электронных компонентов схемы, обеспечив низкую стоимость и высокую надежность.
- Алгоритм вычислений имеет простую программную реализацию, лёгкую для воспроизведения начинающими специалистами.
Список использованной литературы
- Кузнецов Д.Н. Современные микроконтроллеры в системах измере-ния, управления, обработки и отображения информации.: учеб. пособие для обучающихся образоват. учереждений высш. проф. Образования / Д.Н. Кузнецов; ГОУВПО «ДОННТУ». – Донецк: ДОННТУ, 2020. – 400 с.:ил., табл.
- Бюджетный вариант измерения TrueRMS.
- LTC1966 Linear Precision Micropower, RMS-to-DC Converter.