Розробка та дослідження методів підвищення ефективності доступу к памў яті при генеруванні та обробленні зображень
ОЛЕКСАНДР АНОПРІЄНКО
Донецький державний технічний універсітет
Проблема прискорення
процесів обробки та генерації зображень є однією з найбільш актуальних.
У звў
язку з цим дедалі ширше вживаються різноманітні методи її вирішення шляхом
паралелізації обчислювальних процесів. Однією з необхідних умов паралелізації
є забезпечення ефективного доступу до памўяті
зображень [1]. Далі розглядаються варіанти вирішення цієї проблеми та дається
їх теоретична та експериментальна оцінка. При цьому для теоретичного аналізу
був використаний математичний апарат стохастичної геометрії [2], а для
експериметального дослідження - імітаційне моделювання процесів обробки
та генерації зображень. Були досліджені як добре відомі технічні рішення,
так і відносно нові (дивись, наприклад, [4-6] ), а також - теоретично можливі.
Одним з найбільш важливих питань при імітаційному моделюванні є вибір моделі "робочого навантаження", тобто тестових зображень. У простішому разі для цієї мети беруться деякі конкретні зображення. Однак такому підходу притаманні значні недоліки: вибір тестових зображень є суттєво субўєктивним, відсутня можливість достатньо гнучкого управління параметрами робочого навантаження з метою дослідження їх впливу на отримані результати, суттєво обмежені можливості аналітичного опису робочого навантаження, що веде до недостатньої узагальненості результатів моделювання. Тому з метою забеспечення достатньо обўєктивного порівняльного дослідження був вибраний підхід, заснований на використанні вірогідностної моделі робочого навантаження. Моделювались зображення, орієнтовані на два варіанту доступу: векторами (при стохастичному лінійчатому скануванні та генерації векторних зображень) та масивами, репрезентованими випуклими багатокутниками.
При моделюванні векторного робочого навантаження передбачалось рівномірне розподілення векторів по полю растра з рівномірним розподіленням їх орієнтації у межах від 0 до 90 градусів. При цьому моделювались три варианти розподілення їх довжини: "навантаження 1" - довжина кожного вектору у межах растру максимальна; "навантаження 2" - довжини векторів розподілені рівномірно; "навантаження 3" - довжини векторів розподілені експоненціально.
Відповідно моделювалось робоче навантаження, репрезентоване випуклими багатокутниками: "навантаження 1" ("образ-1") - рівномірне розподілення прямокутників по полю растра з рівномірним розподіленням їх розмірів; "навантаження 22 ("образ-2") - рівномірне розподілення багатокутників по полю растра з рівномірним розподіленням їх розмірів; "навантаження 3" ("образ-3") - рівномірне розподілення багатокутників по полю растра з експоненціальним розподіленням їх розмірів.
При аналізі розглядались варіанти прискорення доступу шляхом відповідного розміщення паралельно доступних елементів памўяті з фіксованим розміщенням на растрі слова доступу (Ф-доступ) та плаваючим (П-доступ) з одним (доступ-1) або кількома варіантами його орієнтації (доступ-2 та доступ-4). Приклади розміщення елементів памўяті та використання різних форматів слова доступу наведені на рис. 1-3.
Як відомо із стохастичної геометрії, якщо фундаментальні регіони деякої решітки мають площу a0, і кожна має криву завдовжки L0, то середнє значення кількості точок пересічення цих кривих з кривою D1 завдовжки L1, кинутої випадково на плоскість дорівнює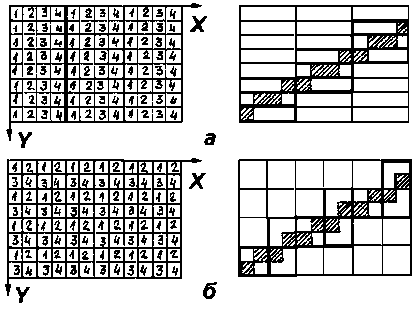
Рис.1. Варіанти розміщення елементів пам'яті та фіксованого одноформатного доступу при обробці векторних зображень
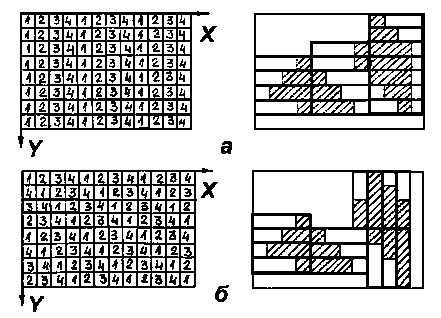
Рис.2. Варіанти розміщення елементів пам'яті та фіксованого доступу при обробці фрагментів зображень типу багатокутників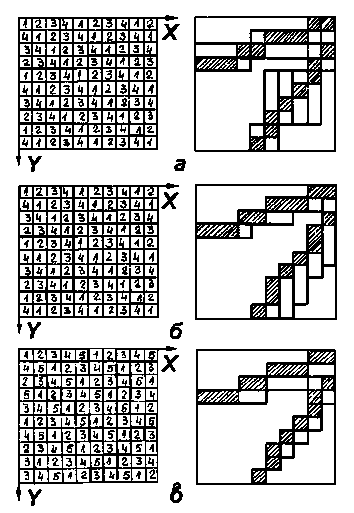
Рис.3. Варіанти розміщення елементів пам'яті та плаваючого багатоформатного доступу при обробці векторних зображень
При одноформатному доступі для навантаження 2 при Х = У = 512 теоретичне значення КА при Wx ®Ґ не перебільшує 1,36.
Виходячі із відомого положення інтегральної геометрії про те, що середня кількість фрагментів, на яке замкнута область D1 площі F1, обмежена однією кривою довжиною L1 буде розділена, коли вона випадково кидається на решітку фундаментальних областей площі a0 з контуром L0, дорівнює
Наведені формули дозволяють при відомих параметрах навантаження оцінити значення коефіцієнту прискорення доступу к пам'яті (порівняно з випадком Wx =Wy = 1) при заданих значеннях Wx и Wy. Практично повний збіг (у межах 1% погрішності) результатів імітаційного моделювання с теоретичними підтвержує ефективність використовуваних методів. Деякі результати дослідження наведені на рис. 4 і 5.
Було також досліджено деякі варіанти ієрархічного кодування зображень, у тому числі впроваджених у вигляді конкретних технічних рішень [5, 6]. На рис. 6 показані, наприклад, результати порівняльного аналізу шляхом моделювання звичайного паралельного доступу (при Wx=16) та апаратно підтриманого ієрархічного коду. При цьому добре видно, що ефективність ієрархічного коду тим вища, чим більше розмір растру зображення.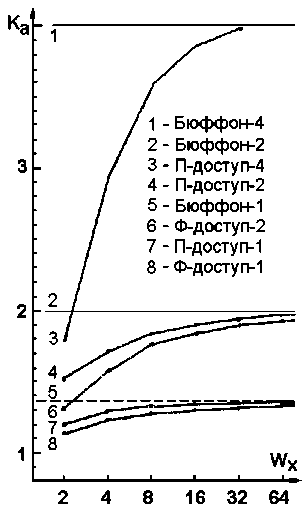
Рис.4. Результати імітаційного моделювання ефективності різних методів доступу при обробці векторних зображень ("Бюффон" - теоретичне вирішення задачі Бюффона)
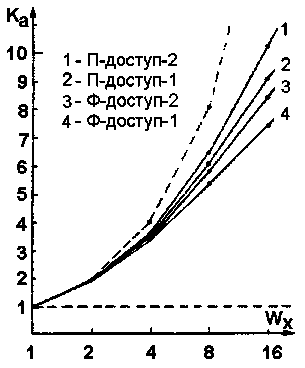
Рис.5. Результати імітаційного моделювання ефектиності різних методів доступу при обробці прямокутних фрагментів зображень
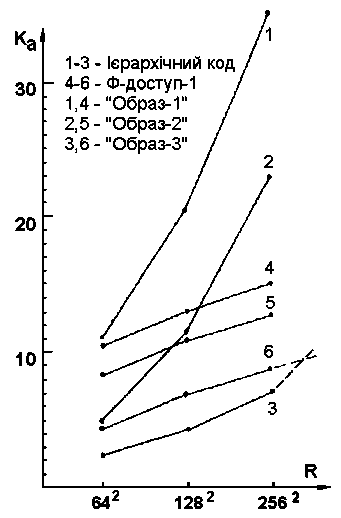
Рис. 6. Прискорення при рiзних розмiрах растра R
Розроблені теоретичні
методи та імітаційні моделі у кожному конкретному випадку дозволяют конкретно
оцінити рівень ефективності відповідних технічних рішень та алгоритмів
з метою їх подальшого впровадження.
Література