A.
Anoprienko
A variant of expansion of classical binary logic and binary notation is presented, which allows to essentially increase their information capacity and efficiency for description of dynamic processes and structures. One of the most effective application areas for the tetracodes is image encoding. As an example the results of experimental research of efficiency of tetracodes for binary image encoding are presented.
2D logical Space
The majority of known modifications of binary and multivalued logic are in essence one-dimensional: the logic values 0 ("false", "no") and 1 ("true", "yes") are set on one axis, and all logic operations are carried out within the limits of this axis [2, 3, 4]. But the variety of human knowledge is such, that the surrounding world can not be always unequivocally described by such a simplified scheme. Mainly because, there are at least two situations, which play an important part in the system of human knowledge: "Don't know" and "Know so much, that cannot answer definitely" [1]. An orthogonal arrangement of "False" and "True" axes permits to include the indicated situations in the formal logic system (Fig. 1). In such two-dimensional logic plane various systems of computer logic can be constructed.
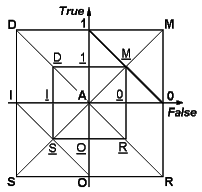
Figure 1. 2D logical Space.
The point A of absolute uncertainty is considered as origin of coordinates. The points 1 and 0 are traditional logic significance "true" and "false". M can be interpreted as "multivalue" or "true and false". M can be interpreted as "equiprobability of true and false". S - "symmetry" of M. I and O - "symmetry" of 1 and 0 respectivly. D and R - two others variants of the "multivalue".
Various logical systems in this space we can specify as LNK = {õ1, õ2, ..., õÊ} with K= 1, 2, 3, 4, ... , where K is an order of the logic; õ1, õ2, ..., õÊ are various logical values from the 2D logical space; N - number of logic order K.
Tetralogic
The variants of logic systems with four conditions present the heaviest theoretical and practical interest. Such systems can be named as "tetralogic". The tetralogic can for example include except two traditional logic significance "true" and 'false" also two additional significance:
L14= {1, 0, À, Ì} (it was proposed in [1] ), L24= {1, 0, Ì, Ì},
L34= {1, 0, S, Ì}, L44= {1, 0, À, Ì}.
The introduction of the suggested logic conditions allows to essentially expand the opportunities of classical binary logic and to adapt it for features of human thinking.
Tetracode
Similar to binary logic being a basis of binary code, tetralogic can be considered as a basis for tetracode. Each position of a tetracode represents a two-bit combination, corresponding to one of the four values of tetralogic. Thus, total amount of bits for the representation of numbers is increased 2 times, but there is an important qualitative change of the code: from a point (i.e. zero-dimensional) number it turns in one-dimensional number, using all space of a numerical axis.
Thus, a number can encode not only an individual value, but also some set of values, rhythmically distributed along a numerical axis. Moreover, depending on the variant of tetracode used, symmetric infringements and uncertainty can be allowed in the set of values. A various tetracodes can be defined as follows (similar tetralogics):
C14 ={1, 0, À, Ì}, C24= {1, 0, Ì, Ì}, C34= {1,0, S,Ì}, C44 = {1,0,À,Ì}.
A principles of the tetracoding can be demonstrated on some examples. We use in examples three positions of the tetracode for demonstrating of corresponding values on the numerical axis with symbols "+" (concrete value), "-" (no value for this punkt), "~" (value for this punkt is not defined), " = " (one of the alternative values), "à", "b"... (one of the alternative values a, b...) for eight points of the axis:
000 = [+ - - - - - - -]; 001= [- + - - - - - -], ...
Tetracode with M and S generate 2mvalues, where m is amount of positions with Ì and S:
00Ì = [+ + - - - - - -]; 0M0 = [+ - + - - - - -]; 1MM = [- - - - + + + +].
0S1 = [- + + - - - - -]; S01 = [- + - - - - + -]; SM0 = [+ + - - - - + +].
1Ì1 = [- - - - - = - =]; M0M = [ = = - - = = - -]; MMM = [a a a a b b b b].
1ÀÀ= [- - - - ~ ~ ~ ~]; 01A® 01M = [- - = = - - - -]; 00A® 00M = [+ + - - - - - - ].
Symbols I and O can be interpreted as "all values except...":
OOO = [- + + + + + + +]; 1I I = [- - - - + + + -]; O10 = [- - + - + + + +].
Symbols D and R can be interpreted as "multivalue with inversion" and "symmetry with inversion" respectively:
D01 = [- + - - + - + +]; R01 = [- + - - + + - +].
The degree of information capacity of tetracode can grow at transition from numerical axis to spaces of greater dimensions.
So, for example, two-dimensional tetracode with total amount of bits sufficient in the case of usual binary coding only for two points, can describe much more complex families of objects on plane (like regular and quasiregular lattices and other structures).
Four-dimensional tetracode, for example, allows to obtain an exceedingly compact descriptions of rhythmical evolution in time of a complex multi-dimensional object. A possibility of representation and use of tetracodes in floating point format is considered as well.
Image encoding
One of the most effective application areas for the tetracode is image encoding. As an example the results of experimental research of efficiency of tetracode for two types of test binary image (Fig. 2) encoding are presented.
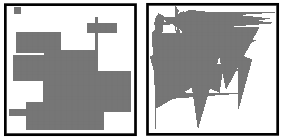
Figure 2. Examples of the test images: “Type A” (left) and “Type
B” (right).
Various algorithms of binary image encoding (Fig. 3) on the basis of tetracode were developed and investigated.
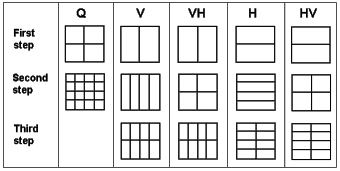
Figure 3. Different
variants of space devision for image encoding on the basis of 2D tetracode.
The main results are as follows:
- the compression of information is more efficient in the majority of cases than by use of such a well known format as gif (Fig. 4, 5);
- the codes obtained contain an important generalised information on some essential attributes of the images: degree of regularity, orientation of basic elements, distribution of elements by sizes, etc.;
- the codes obtained can be effectively used for further analysis and processing of images.
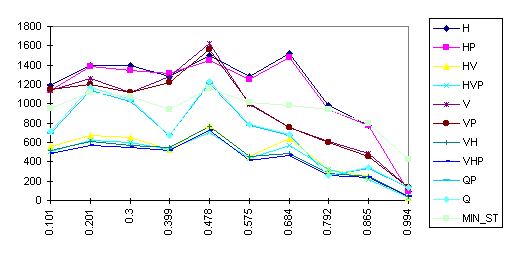
Figure 4. The size (bytes) of various tetracodes in compare with GIF (MIN_ST) for images “Type A” (256 x 256) as function of the black pixels density.
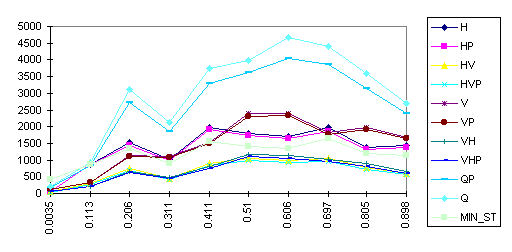
Figure 5. The size (bytes) of various tetracodes in compare with
GIF (MIN_ST) for images “Type B” (256 x 256) as function of the black pixels
density
The concept of tetralogic
and tetracodes seems to be quite fruitful both from theoretical point of
view and from the point of view of future practical applications in simulation
systems, image recognition and computer graphics - the most closely adjoining
with problems of extreme information complexity of the surrounding world.
REFERENCES
[1] N. D. Belnap, A useful four-valued logic. Modern uses of multiple-valued logic. Epstein G., Dunn J. M. (eds.). Proceedings of the 1975, International Symposium of Multiple-valued Logic. Reidel (1976).
[2] J. Lukasiewicz O pojeciu mozliewosci, Ruch Filozoficzny. Lwow. R. 5. ¹ 9 (1920).
[3] W. Heise, P. Quattrocchi, Informations- und Codierungstheorie. Mathematische Grundlagen der Daten-Kompression und -Sicherung in diskreten Kommunikationssystemen. Berlin, Heidelberg, Springer-Verlag, 476 z. (1995).
[4] E. L. Post, Introduction to a General Theory of Elementary Propositions, American Journal of Mathematics. Vol. 43. ¹ 3 (1921).
Anoprienko A. Tetralogic and tetracodes: an effective method for information coding // 15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics. Berlin, August 24-29, 1997. Vol. 4. Artificial Intelligence and Computer Science. - Berlin: Wissenschaft und Technik Verlag. - 1997. - P. 751-754.