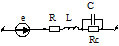Вернуться в библиотеку
УДК 621.316.925
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В РАСПРЕДЕЛИТЕЛЬНЫХ СЕТЯХ 6-10 КВ
Сивокобыленко В.Ф., Лебедев В.К., Коваленко Е.В., Маслова А.И.
Донецкий национальный технический университет
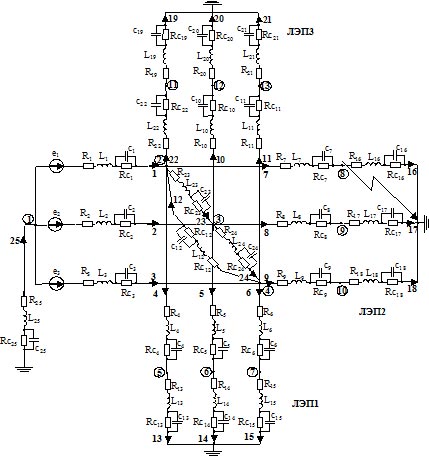
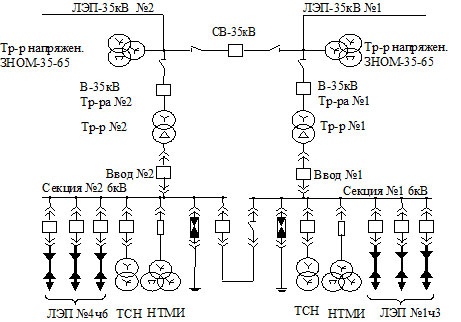
Постановка задачи и анализ последних исследований. Однофазные замыкания на землю являются самым распространённым видом повреждения в электрических сетях среднего класса напряжения (в пределах до 85-90% от общего числа нарушений нормальной работы сетей в зависимости от их назначения и конструк-тивного исполнения). В сложившихся условиях сильной изношенности изоляции в подавляющем большинстве случаев они развиваются в междуфазные короткие замыкания или многоместные пробои изоляции с групповым выходом из строя электрооборудования, сопровождаясь большим материальным ущербом и недоотпуском электроэнергии потребителям. Поэтому справедливо считается, что основным направлением повышения на-дёжности работы электрических сетей является борьба с однофазными замыканиями на землю. Именно поэто-му в большинстве технически развитых странах, в том числе и в Украине, в настоящее время интенсивно ве-дутся работы по совершенствованию условий функционирования электрооборудования в распределительных сетях. Математическому моделированию переходных процессов в сетях 6 – 10 кВ посвящены многие работы [1-4 и др.]. В этих работах исследовались перенапряжения в сетях при глухом и дуговом замыкании на землю. Однако указанные модели основаны на явном методе численного интегрирования дифференциальных уравне-ний элементов сети, которые во многих случаях приводят к нарушению численной устойчивости и не позволя-ют исследовать многие практически важные случаи переходных процессов. Задача исследования. Целью настоящей работы является разработка математической модели распре-делительной сети для анализа переходных процессов, основанной на использовании дискретных схем замещения ее отдельных элементов для обеспечения численной устойчивости модели. Изложение основного материала. Типовая схема распределительной электрической сети (рис.1) со-держит питающие трансформаторы, воздушные и кабельные ЛЭП, нагрузку и др. элементы.
|
Рисунок 1 – Типовая схема электроснабжения промышленного объекта
Схема замещения такой сети (рис.2) содержит активные и индуктивные сопротивления элементов, а также емкостное и активное сопротивления изоляции сети. С целью автоматизации формирования математиче-ской модели электрической системы любой степени сложности будем использовать ее граф и матрично-векторную запись законов Ома и Кирхгофа [5].
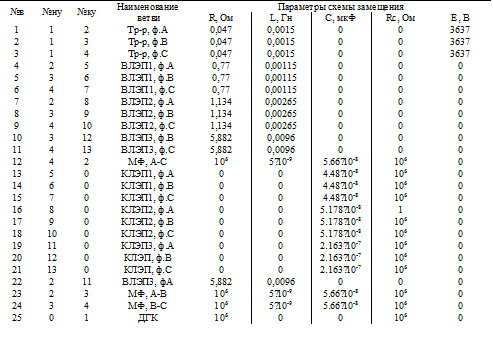
Схему замещения каждого из элементов схемы будем представлять обобщенной ветвью (рис.3) с по-следовательно-параллельным соединением ее R,L,С-элементов, которые учитывают сопротивления самого эле-мента (R, L) и его изоляции на землю (C, Rc).
Рисунок 2 – Схема замещения для одной из секций 6 кВ типовой схемы
Рисунок 3 – Схема замещения обобщенной ветви сети
При моделировании стационарного режима общее сопротивление такого (рис.3) n-го элемента сети бу-дет равно:
|
Z
n
=R+j·w·L+[Rc·(j·w·C·Rc+1)
-1
],
|
(1) |
где: w - частота напряжения питающей сети, n – количество ветвей схемы. Расчет доаварийного режима заданной схемы и глухого замыкания фазы на землю можно выполнить, например, методом контурных токов. Для этого определяем матрицы сопротивлений ветвей и контуров схемы:
|
Zv=diag(Zi), |
(2) |
|
Zk=B
T
·Zv·B,
|
(3) |
где: B – матрица главных контуров, количество которых равно числу хорд графа, а i = 1,2,…,n.
Формируем вектор контурных ЭДС и контурных токов:
|
Ek=B
T
·Ev,
|
(4) |
|
Ik=Zk
-1
·Ek,
|
(5) |
где Ev- вектор источников ЭДС, состоящий из ЭДС ветвей e
i
.
Находим напряжения, токи и мощности ветвей:
|
Iv=B·Ik, |
(6) |
|
Uv=Ev-Zv·Iv, |
(7) |
|
Sv=diag(Uv)·Iv
*
,
|
(8) |
где Iv
*
- сопряженный вектор тока ветвей.
Определяем напряжения в узлах схемы:
|
Uuzl=(P·P
T
)·P
-1
·Uv,
|
(9) |
где P – матрица соединений ветвей с узлами схемы. Для анализа переходных процессов, в отличие от [1-4], будем использовать дискретную математиче-скую модель электрической схемы, основанную на замене производных в исходных дифференциальных урав-нениях модели их конечными разностями первого, второго или более высоких порядков. В литературе [6] та-кую замену производных выполняют путем использования формул дифференцирования назад (ФДН):
|
(dy/dx)
k+1
=-(1/h)·a
s
·y
k+1-s
,
|
(10) |
где a
s
- постоянные коэффициенты на каждом шаге интегрирования, которые для метода ФДН второго порядка (р=2) соответственно равны a
0
=1,5 , a
1
=-2 , a
2
=0,5 .
Формулу (10) называют формулой дифференцирования назад, поскольку здесь производная функции в k + 1-й точке аппроксимируется по p + 1 значениям этой функции в предыдущих точках. Ее также называют формулой Гира.
Для заданной схемы с учетом рис.3 и (10) на каждом временном шаге расчета h будем производить рас-чет матриц мгновенных дискретных значений сопротивлений и векторов эквивалентных ЭДС ветвей, которые соответственно равны:
|
Z=diag[R+(a
0
/h)·L+(h·Rc)/(a
0
·Rc·C+h)],
|
(11) |
|
Eekv
(k)
=(L/h)·a
s
·i
(k+1-s)
-(a
s
·uc
(k+1-s)
)/(Rc·C),
|
(12) |
где uc и i - мгновенные значения напряжения на емкости и тока на k-ом шаге расчета.
Выражения (10) – (12) представлены с учетом операторов векторизации [7].
Расчет переходных процессов будем выполнять с использованием (11 - 12) в соответствии с алгорит-мом, справедливом для анализа стационарных режимов. Например, в случае использования метода узловых напряжений, уравнения для расчета выглядят следующим образом:
|
Yuzl=P·Z
-1
·P
-1
,
|
(13) |
|
Uuzl(t)=Yuzl
-1
·P·Z
-1
·(e(t)-Eekv),
|
(14) |
|
Uv(t)=P
T
·(e(t)-EekvUuzl(t)),
|
(15) |
|
i(t)=Z
-1
·(e(t)-Eekv-Uv(t)),
|
(16) |
|
uc
(k+1)
=((h·Rc·i(t)
(k+1)
)/(a
0
·Rc·C+h))-((Rc·C)/(a
0
·Rc·C+h))·uc
(k+1-s)
,
|
(17) |
Достоинство такого представления модели для анализа переходных процессов заключается в том, что алгоритм расчета установившегося и переходного процессов остается одинаковыми. Отличие состоит в том, что на каждом шаге расчета переходного процесса необходимо обновлять значения сопротивления и ЭДС ветвей.
Дискретные модели отличаются высокой численной устойчивостью и для рассматриваемых процессов другие подходы не всегда позволяют выполнить расчет, как это уже отмечалось выше.
Покажем пример анализа переходного процесса в схеме электроснабжения промышленного объекта. Типовая схема объекта представлена на рис. 1, ее схема замещения на рис.2. Приведем граф сети (рис.4) и ис-ходные данные (табл.1), где представлены параметры собственных и взаимных сопротивлений трансформатора, воздушных линий (ВЛЭП), кабельных линий (КЛЭП) и дугогасящей катушки для заземления нейтрали сети.
Рисунок 4 – Граф электрической сети
Граф электрической сети содержит 13 узлов (кроме нулевого базисного), ветви хорды 1 – 12, ветви де-рева 13 – 25 для соответствующих элементов сети (табл.1).
Таблица 1 – Параметры схемы замещения
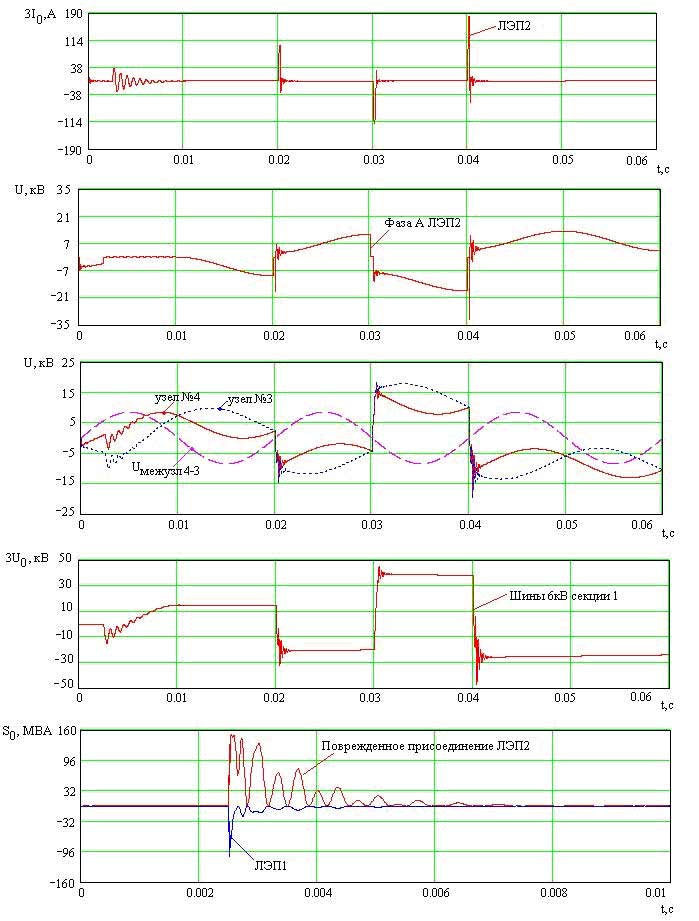
Отметим, что при отсутствии дугогасящей катушки и глухом замыкании на землю в узле 8 (ветвь 16) ток нулевой последовательности составил 1,074 А. Как известно, наибольшие перенапряжения при замыкании фазы на землю могут возникать, если мо-мент замыкания происходит в максимум напряжения поврежденной фазы, а погасание дуги - при переходе че-рез "ноль" высокочастотной составляющей тока замыкания или составляющей промышленной частоты. На рис.5 приведены осциллограммы многократных замыканий на землю фазы А ветви 16 (рис.2).
Рисунок 5 – Осциллограммы дуговых замыканий на землю в сети с изолированной нейтралью
Из осциллограмм следует, что при первом замыкании фазы на землю напряжения на здоровых фазах не превышают 2,6 значений амплитуды Uф, но при последующих пробоях напряжения на здоровых фазах возрас-тают до 4,5Uф, т. е. при таком виде замыкания происходит процесс эскалации напряжений. Аналогичным обра-зом происходит нарастание напряжения на поврежденной фазе. На рисунке также представлены осциллограм-мы тока нулевой последовательности поврежденного присоединения ЛЭП2. Ток нулевой последовательности поврежденного присоединения находится в противофазе с токами нулевой последовательности остальных при-соединений. При замыкании фазы на землю, мощность, как правило, направлена к месту повреждения, которое находится в зоне действия реле направления мощности. Мощность рассчитываем как произведение p(3Uо) на 3Iо.
На рис.5 показан также характер изменения при дуговых замыканиях мощности нулевой последова-тельности ЛЭП1 и ЛЭП2, что позволяет использовать эти данные при разработке принципа действия и алго-ритма направленной защиты.
Выводы:
- Разработана математическая модель системы электроснабжения напряжением 6-10 кВ, особенно-стью которой является использование дискретных моделей ее элементов.
- Дискретная модель обеспечивает высокую численную устойчивость решения систем дифференци-альных уравнений и может быть рекомендована для анализа перенапряжений и поведения устройств релейной защиты электрических сетей при глухих и дуговых замыканиях на землю.
- Показан пример расчета переходных процессов с помощью разработанной математической модели в сети 6кВ.
ЛИТЕРАТУРА
- Журахівський А.В., Кенс Ю.А., Горбатський А.А., Романишин В.В., Кобрій Б.В. Пристрої захисту трансформаторів напруги від ферорезонансних процесів в електричних мережах з ізольованою нейтраллю. \\ Збірник наукових праць Донецького Національного Технічного університету. Серія: “Електротехніка і енергетика”, випуск 21: Донецьк: ДонНТУ, 2000. с.(9-13).
- Сивокобыленко В.Ф., Лебедев В.К., Левшов А.В., Махинда Сильва Повышение надежности работы сетей собственных нужд электростанций при замыкании фазы на землю.\\ Збірник наукових праць Донецького Національного Технічного університету. Серія: “Електротехніка і енергетика”, випуск 21: Донецьк: ДонНТУ, 2000. с.(17-21).
- Журахівський А.В., Кенс Ю.А., Мединський Р.В., Засідкович Н.Р. Особливості розрахунку напруги зміщення нейтралі трифазних електромереж. \\ Збірник наукових праць Донецького Національного Технічного університету. Серія: “Електротехніка і енергетика”, випуск 50: Донецьк: ДонНТУ, 2002. с.(102-106).
- Журахівський А.В., Кенс Ю.А., Батенько П.В., Мельник С.Т. Захист трансформаторів напруги від ферорезонансних процесів в електричних мережах з заземленою нейтраллю. \\ Збірник наукових праць Донецького Національного Технічного університету. Серія: “Електротехніка і енергетика”, випуск 21: Донецьк: ДонНТУ, 2000. с.(13-17).
- В.Ф. Сивокобыленко, В.К. Лебедев Переходные процессы в системах электроснабжения собственных нужд электростанций. Донецк 2002. – 134с.
- В.С. Перхач. Математичні задачі електроенергетики. – Львів.: Видавництво при Львівському Державному Університеті видавничого об`єднання «Вища Школа», 1982. – 378с.
- MATHCAD 6.0 PLUS. Финансовые, инженерные и научные расчеты в среде Windows 95. / Перевод с англ. – М.: Информационно-издательский дом «Филинъ», 1996. – 712с.