на тему: Исследование и разработка компьютерных систем решения задач комбинаторной оптимизации с помощью генетических алгоритмов
выполнил студент группы АСУ96а
Хмелевой Сергей
Преподаватель: Скобцов Ю.А.
Анализ состояния исследуемого вопроса
Основные операции в генетических алгоритмах
Сущность генетических алгоритмов
Оптимизация простой одномерной функции
Цели работы и решаемые в ней задачи
Существует достаточно большой круг задач, для которых еще не исследовали достаточно быстрых алгоритмов. Многие из этих проблем - это задачи оптимизации во всех их проявлениях. Нахождение кратчайшего пути, наибольшей прибыли, наименьших затрат - эти задачи встречаются в бизнесе, и, конечно же, не только в бизнесе, каждый день.
Классические методы оптимизации дают результаты. Они способны быстро найти экстремум любой функции. Для многих сложных оптимизационных проблем мы их и используем. Они не гарантируют оптимальное значение, но могут быстро найти локальный экстремум, первое более-менее оптимальное решение. А при наличии нескольких локальных экстремумов начинаются проблемы. К тому же при увеличении объемов решаемых задач скорость решения также может сильно падать.
Вообще - то практически любую абстрактную задачу можно представить как поиск среди множества потенциальных решений. Таким образом, решая какую - либо задачу, мы можем представить процесс ее решение как оптимизационный процесс, где необходимо найти оптимум (максимум, минимум). Для маленьких пространств поиска обычно хватает простых "истощающих" алгоритмов, для больших же необходимы специальные, "интеллектуальные" методы. Генетические алгоритмы относятся к таким методам. Вообще-то они относятся к классу вероятностных алгоритмов, но они очень отличаются от традиционных случайных алгоритмов. Они являются комбинацией прямого и стохастического поиска. Вторая их важная черта - использование многоточечного поиска. Они ищут решение во множестве точек, комбинируя и меняя их, не довольствуясь единственной точкой, которая используется в других методах.
Различные методы (допустим, с использованием производной), используют собственную итеративную технику улучшения результатов. В течение одной итерации они ищут лучшую точку в окрестностях данной точки (поэтому такие методы также называют методами локального поиска). Если новая точка лучше предыдущей, она становится базовой, начинается новая итерация. Это продолжается, пока прирост функции не уменьшится практически до нуля. Логично, что такие методы не могут найти глобальный оптимум, а только локальный, значение которого зависит от стартовой точки. Глобальный же оптимум может быть найден только случайно. Для повышения вероятности нахождения глобального оптимума используется множественный эксперимент с различными начальными точками.
Что же такое генетические алгоритмы? Как они зародились? На каких принципах они построены?
Само название - генетические объясняет, откуда взялась идея. Стараниями Чарльза Дарвина весь мир узнал такие слова, как эволюция, естественный отбор, чуть позже - гены, мутация. Наблюдение за процессом эволюции, попытка как-то повторить этот процесс и дала как результат генетические алгоритмы. Сама идея заключается в следующем.
Как известно, в природе действует жесткий закон - естественный отбор. Будь лучше других, или погибнешь. Вся информация о живых существах хранится в их генах. При рождении потомства они наследуют часть генов от одного родителя, часть от другого. Таким образом, имеется возможность получения от родителей их лучших качеств, потомок может быть лучше каждого из родителей, получив в наследство лучшие их особенности, и не получив худшие. Естественно, возможна и обратная ситуация. Но тогда вступает в действие естественный отбор. Если потомок хуже других собратьев, он не сможет убежать от хищника, или не сможет найти себе пищу. Короче - выживают лучшие. Для того чтобы возможно было возникновение новых видов, нам помогает радиация. Она нарушает информацию в генах, повреждает их. Если повреждение сильное, потомство не выживает, если слабое - возможно возникновение новых, неизвестных ранее качеств. Если это изменение передастся по наследству, то тогда рождается новый вид с совершенно другими свойствами.
Этот же принцип заложен и в генетических алгоритмах. Имеется некоторая строка, в которой закодированы некие особенности организма.
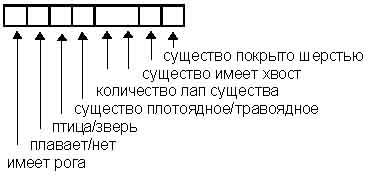
Рис.1. Представление в генетических алгоритмах.
Наличие в ячейках этой строки 1 или 0 определяет существо.
Конечно, этот рисунок весьма упрощен, но он дает наглядное представление о представлении в генетических алгоритмах.
Основные операции в генетических алгоритмах.
Основными операциями в генетических алгоритмах являются кроссовер и мутация.
Кроссовер: имеем два экземпляра одного вида (их называют стрингами). Делим эти стринги на две произвольные части (одинаковой длины в каждом стринге). Затем соединяем их, беря из каждого стринга по противоположной части. Получаем два потомка, которые имеют часть свойств каждого родителя, но не имеют общих подстрок.
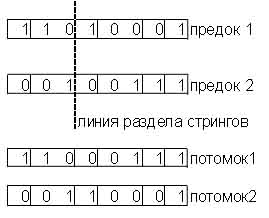
Рис.2. Классический кроссовер.
Мутация: имеем стринг
1 0 1 1 1 0 0 0
В процессе мутации случайным образом меняем любой из генов стринга - любую ячейку на противоположную. Можем получить такой результат мутации:
1 0 1 1 1 0 1 0
Сущность генетических алгоритмов.
Сущность ГА заключается в следующем: имеем достаточно большую популяцию определенного вида стрингов. Для этого вида стрингов имеется также некая функция годности (Fitness), которая определяет численное значение годности стрингов для данной задачи. Цель генетического алгоритма - подобрать такой стринг, который имел бы оптимальную (минимальную, максимальную) функцию годности. Для этого происходит выбор из всего множества стрингов с наибольшей функцией годности (естественный отбор) и получением от них потомства, хранящего некоторые свойства родителей. Далее цикл повторяется. Для того чтобы не зависеть от возможной ограниченности базового набора стрингов и неспособности на их основе построить оптимальный стринг, используют мутации. Таким способом получают совершенно новые стринги. Естественно, чтобы мутации не мешали естественным процессам, их применяют достаточно редко.
Оптимизация простой одномерной функции.
Имеем простую одномерную функцию вида y=f(x). Необходимо найти максимум функции (минимум), т.е. значение х, при котором y принимает наибольшее (наименьшее) значение.
Для нахождения результата представим хромосому двоичным вектором размера n. Чем больше n, тем выше будет точность нахождения результата. В хромосому (стринг) мы записываем значение х, преобразованное в двоичный вид. Естественно, сразу определяется, сколько бит отводится под целую часть числа, а сколько под дробную. Функция годности (фитнесс) в данном случае очевидна - это f(x). В случае, если решение ограничено какими-то пределами (допустим, от 0 до 2), также составляется ремонтирующий алгоритм, который исправляет стринги, вышедшие за эти пределы.
Создаем множество экземпляров стрингов (популяция зависит от пределов, в которых ищется решение). Затем начинаем бесконечный цикл: отбор лучших хромосом, получение от них потомства (кроссовер). Время от времени используется мутация: случайным образом меняется один из битов хромосомы. Этот цикл повторяется до тех пор, пока лучший результат на предыдущем цикле не будет отличаться от лучшего результата на текущем цикле на величину е.
Результаты:
Для функции f(x)=x*sin(10*pi*x+1.0) необходимо найти х в пределах [-1..2], который максимизирует эту функцию.
График функции представлен на рис. 3.
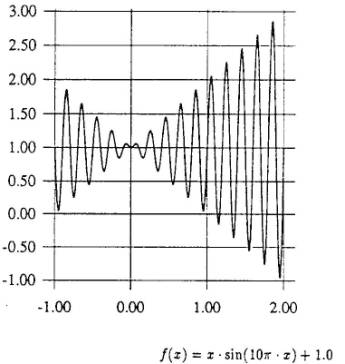
рис.3. график функции f(x).
При размере популяции = 50, вероятности кроссовера = 0.25, вероятности мутации = 0.01 за 150 итераций был найден результат: 2.850227 при хмах=1.8500773. Аналитическими методами найден результат при хмах=1.85: f(1.85)=1.85*sin(18 ? + ? /2)+1.0 = 2.85.
Два заключенных содержатся в отдельных камерах и не могут общаться друг с другом. Каждый заключенный на допросе может выдать или не выдать другого. Если только один заключенный выдает другого, он награждается, а другой наказывается. Если оба выдают друг друга, они оба наказываются и подвергаются пыткам. Если никто не выдал друг друга, оба умеренно награждаются. С точки зрения индивидуального заключенного, ему выгоднее все время выдавать другого заключенного, за это он будет получать больше, чем если оба будут молчать. Но ведь другой заключенный думает так же. А если оба выдают друг друга, оба будут наказаны. В этом и заключается дилемма заключенных - определить стратегию поведения в такой ситуации. Эта дилемма может бать представлена как игра между двумя игроками, где за каждый ход каждому игроку предстоит решить, выдавать или не выдавать оппонента. В конце хода игроки знакомятся с ответом оппонента и получают за ответ очки:
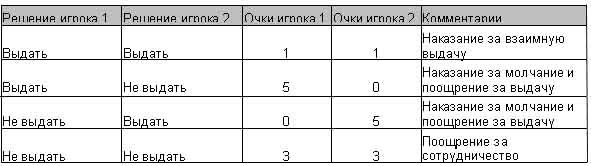
Таблица 1. Дилемма заключенных.
Решение дилеммы с помощью ГА.
Прежде всего, необходимо как-то представить стратегию (т.е. возможное решение). Достаточно при приеме решения учитывать решения и ответы за три предыдущих хода. Таким образом, с четырьмя возможными вариантами ответов за каждый ход, имеем 4*4*4 = 64 варианта хромосомы (вида трех предыдущих ходов). Стратегия в таком случае может быть представлена с помощью перебора всех возможных ситуаций (показывающих действия за предыдущие три хода) и указания, какой ход необходимо сделать сейчас. Таким образом, стратегия может быть представлена строкой из 64 битов. Допустим, строка начинается с битов
(1 0 1 …), (1-не выдавать, 0-выдавать). Это означает:
· если предыдущие три хода были - выдавать всех (0,0 0,0 0,0), то не выдавать.
· Если предыдущие три хода были: (0,0 0,0 0,1), то выдавать.
· Если предыдущие три хода были: (0,0 0,0 1,0), то не выдавать.
И т.д.
Чтобы представить стратегию, которая была в самом начале игры, необходимо еще 6 битов. Таким образом всего хромосома будет содержать 70 битов.
Строка из семидесяти битов определяет, что игрок будет делать в различных ситуациях и полностью определяет индивидуальную стратегию. Строка из семидесяти битов также подходит для хромосомы игрока при использовании в эволюционном процессе.
Генетический алгоритм Аксельрода (Axelrod) для разработки стратегии дилеммы заключенных работает в 4 стадии:
· Выбор начальной популяции. Каждому игроку присваивается случайным образом заполненная строка из семидесяти бит, представляющих стратегию.
· Тест каждого игрока, чтобы определить ее эффективность. Каждый игрок использует стратегию, записанную в его хромосоме при игре с другими игроками. Очки игрока - сумма всех очков, полученных во всех играх. Игроки с максимальным количеством очков допускаются к дальнейшей игре.
· Выбор игроков для размножения. Выбирают игроков с количеством очков выше среднего и разрешают им спариваться. Игрокам со средним количеством очков разрешено одно спаривание, с очками выше среднего - два. Игроки с количеством очков ниже среднего не спариваются.
· Все игроки, получившие разрешение на спаривание, случайным образом скрещиваются, от них получается по два потомка. Это делается, используя два генетических оператора: кроссовер и мутация.
После этих четырех стадий мы получаем новую популяцию. Члены этой популяции могут быть очень не похожими друг на друга, но количество очков у них будет приблизительно одинаковым. С каждой новой итерацией среднее количество очков будет повышаться, а состав популяции будет становиться все более похожим.
Итоги работы:
В результате работы было представлено несколько стратегий с максимальным количеством очков. Вот они:
· "Не шатайте лодку": продолжать кооперацию (1,1 1,1 1,1)
· "Провокатор": после установления кооперации предать (1,1 1,1 1,0)
· "Зуб за зуб, глаз за глаз": отвечать противнику тем же, что он сделал перед этим (1,0 0,1 1,1)
· "Простить грехи: забыть об обиде (0,1 1,1 1,1)
· "Кровная месть": несотрудничество (0,0 0,0 0,0)
Задача коммивояжера (ЗК) считается классической задачей генетических алгоритмов. В теории генетического программирования эта задача читается очень важной, чуть ли не матерью остальных задач. Почему?
Причин много. Прежде всего, эта задача очень проста: путешественник (или коммивояжер) должен посетить каждый из базового набора городов и вернуться к исходной точке. Имеется стоимость билетов из одного города в другой. Необходимо составить план путешествия, чтобы сумма затраченных средств была минимальной. Поисковое пространство для ЗК- множество из N городов. Любая комбинация из N городов, где города не повторяются, является решением. Оптимальное решение - такая комбинация, стоимость которой (сумма из стоимостей переезда между каждыми из городов в комбинации) является минимальной.
ЗК - достаточно старая проблема: она была сформулирована еще в 1759 году (под другим именем). Термин "Задача коммивояжера"был использован в 1932г. в немецкой книге "The traveling salesman, how and what he should to get commissions and be successful in his business", написанную старым коммивояжером.
Задача коммивояжера была отнесена к сложным задачам. Существуют строгие ограничения на последовательность, и количество городов может быть очень большим (существуют тесты, включающие несколько тысяч городов).
Кажется естественным, что представление тура - последовательность (i1, i2, … , in), где (i1, i2, … , in) - числа из множества (1 … n), представляющие определенный город. Двоичное представление городов не будет иметь никаких преимуществ. Напротив, двоичное представление будет требовать специального ремонтирующего алгоритма, т.к. изменение одиночного бита может повлечь неправильность тура.
В настоящее время существует три основных представления пути: соседское, порядковое и путевое. Каждое из этих представлений имеет их собственные "генетические" операторы, все они очень сильно различаются. Объединяет их только одно - тема.
Соседское представление представляет тур как список из n городов. Город J находится на позиции I только в том случае, если маршрут проходит из города I в город J. Например, вектор (2 4 8 3 9 7 1 5 6) представляет следующий тур: 1-2-4-3-8-5-9-6-7 . Каждый маршрут имеет только одно соседское представление, но некоторые векторы в соседском представлении могут представлять неправильный маршрут. Например, вектор (2 4 8 1 9 3 5 7 6) обозначает маршрут 1-2-4-1..., т.е. часть маршрута - замкнутый цикл. Это представление не поддерживает классическую операцию кроссовера. Три операции кроссовера были определены и исследованы для соседского представления: alternating edges (альтернативные ребра), subtour chunks (куски подтуров), heuristic crossovers (евристический кроссовер).
Кроссовер alternating edges строит потомков, выбрав (случайно) ребро от первого родителя, потом следующее ребро от второго, потом опять следующее от первого и т.д. Если новое ребро представляет замкнутый цикл, берут случайный угол из того же родителя, который еще не выбирался и не образуют замкнутого цикла. Для примера, один из потомков родителей
P1 = (2 3 8 7 9 1 4 5 6) и
Р2 = (7 5 1 6 9 2 8 4 3)
Может быть
П1 = (2 5 8 7 9 1 6 4 3),
где процесс начинался от угла (1,2) родителя Р1, продолжая до угла (7,8), вместо которого выбран угол (7,8), поскольку тот образуют замкнутый цикл.
Кроссовер subtour chunks создает потомков, выбирая (случайно) подтур от одного из родителей, затем случайной длины кусок от другого из родителей, и т.д. И опять, если на каком - то уровне образуется замкнутый цикл, он решается аналогичным образом (выбирается другой случайный подтур, который еще не выбирался, из этого же родителя).
Heuristic crossovers строит потомков, выбирая случайный город как стартовую точку для маршрута - потомка. Потом он сравнивает два соответствующих ребра от каждого из родителей и выбирает белее короткое. Затем конечный город выбирается как начальный для выбора следующего более короткого ребра из этого города. Если на каком-то шаге получается замкнутый тур, тур продолжается любым случайным городом, который еще не посещался.
Преимущества этого представления - в том, что она позволяет схематически анализировать подобные маршруты. Это представление имеет в основании натуральные "строительные блоки" - ребра, маршруты между городами. Например, схема ( * * * 3 * 7 * * * ) описывает множество всех маршрутов с ребрами ( 4 3 ) и ( 6 7 ). Основной же недостаток данного представления - в том, что множество всех его операций очень бедно. Кроссовер alternating edges часто разрушает хорошие туры, которые были у обоих родителей до применения этой операции. Кроссовер subtour chunks имеет лучшие характеристики, чем первый, благодаря тому, что его разрушительные свойства меньше. Но все равно его эксплуатационные качества все же достаточно низки. Кроссовер heuristic crossover, конечно же, наилучший оператор для данного представления. Причина - в том, что предидущие операции слепы, они не берут в расчет настоящую длину ребер. С другой стороны, heuristic crossover выбирает лучшее ребро из двух возможных. Может получиться, что дальнейший путь будет невозможен и придется выбирать ребро, длина которого неоправданно большая. К тому же, производительность этой операции нестабильна. В трех экспериментах на 50, 100 и 200 городах система нашла туры с 25%, 16% и 27% оптимального, приблизительно за 15000, 20000 и 25000 итераций соответствено.
Порядковое представление представляет тур как список из n городов; i-й элемент списка - номер от 1 до n-i-1. Идея порядкового представления состоит в следующем. Есть несколько упорядоченных списков городов С, которые служат как точки связи для списков с порядковым представлением. Предположим, для примера, что такой упорядоченный список прост:
(1 2 3 4 5 6 7 8 9).
Тогда тур
1-2-4-3-8-5-9-6-7
будет представлен как список l из ссылок,
l=(1 1 2 1 4 1 3 1 1)
и может быть интерпретирован следующим образом:
Так как первый номер списка l 1, берем первый город из списка С как первый город из тура (город номер 1), и исключаем его из списка. Часть маршрута - это
1
Следующий номер в списке l также 1, поэтому берем первый номер из оставшегося списка. Так как мы исключили из списка С 1-й город, следующий город - 2. Исключаем и этот город из списка. Маршрут:
1 - 2
Следующий номер в списке l - 2. Берем из списка С 2-ой по порядку оставшийся город. Это - 4. Исключаем его из списка. Маршрут:
1 - 2 - 4
Следующий номер в списке l - 1. Берем из списка С 1-й город - с № 3. Имеем маршрут
1 - 2 - 4 - 3
Следующий в списке l - 4, берем 4-й город из оставшегося списка (8).
Маршрут:
1 - 2 - 4 - 3 - 8
Следующий номер в списке l - 1. Берем из списка С 1-й город - с № 5. Маршрут:
1 - 2 - 4 - 3 - 8 - 5
Следующий номер в списке l - 3. Берем следующий город из списка (9). Удаляем его из С. Маршрут:
1 - 2 - 4 - 3 - 8 - 5 - 9
Следующий номер в списке l - 1, поэтому берем первый город из текущего списка С и следующий город маршрута (город номер 6), и удаляем его из С. Частичный маршрут имеет вид:
1 - 2 - 4 - 3 - 8 - 5 - 9 - 6
Последним номером в списке l всегда будет 1, поэтому берем последний оставшийся город из текущего списка С и последний город маршрута (город номер 7), и удаляем его из С. Окончательно маршрут имеет вид:
1 - 2 - 4 - 3 - 8 - 5 - 9 - 6 - 7
Основное преимущество порядкового представления - в том, что классический кроссовер работает! Любые два маршрута в порядковом представлении, обрезанные на любой позиции и склеенные вместе, породят два потомка, каждый из которых будет правильным туром. Например, два родителя
p1 = (1 1 2 1| 4 1 3 1 1) и
p2 = (5 1 5 5 | 5 3 3 2 1),
которые обозначают соответственно маршруты
1 - 2 - 4 - 3 - 8 - 5 - 9 - 6 - 7 и
5 - 1 - 7 - 8 - 9 - 4 - 6 - 3 - 2,
с точкой разреза, обозначенной " | " породят следующих потомков:
o1 = (1 1 2 1 5 3 3 2 1) и
o2 = (5 1 5 5 4 1 3 1 1).
Эти потомки обозначают маршруты
1 - 2 - 4 - 3 - 9 - 7 - 8 - 6 - 5 и
5 - 1 - 7 - 8 - 6 - 2 - 9 - 3 - 4
Легко заметить, что части маршрута слева от линии разреза не изменились, тогда как части маршрута справа от линии разреза расположились в достаточно случайном порядке. Откровенно слабые показатели этого представления также подтверждают первое впечатление о слабой возможности использования его.
Путевое представление - это, возможно, наиболее естественное представление тура. Например, тур
5 - 1 - 7 - 8 - 9 - 4 - 6 - 2 - 3
представлен просто как
(5 1 7 8 9 4 6 2 3).
До последнего времени для путевого представления было известно три операции кроссовера: частично отображенный - partially-mapped (PMX), порядковый - order (OX), циклический - cycle (CX) кроссоверы.
PMX - строит потомков, выбирая подпоследовательность из тура от одного из родителей и сохраняя порядок и последовательность наибольшего из возможного числа городов другого родителя. Подпоследовательность маршрута выбирается двумя случайными точками разреза. Например, два родителя (разрезы отмечены " | ")
p1= (1 2 3 | 4 5 6 7 | 8 9) и
p2= (4 5 2 | 1 8 7 6 | 9 3)
могут получить потомков следующим способом. Во-первых, сегменты между точками обреза меняются местами (символом "Х" обозначается неизвестный символ).
о1= (х х х | 4 5 6 7 | х х) и
о2= (х х х | 1 8 7 6 | х х)
также этот обмен определяет серию преобразований данных:
1 <-> 4, 8 <-> 5, 7<-> 6 и 6 <-> 7
теперь мы можем заполнить остальные города, для которых нет конфликтов, из другого родителя:
о1= (х 2 3 | 4 5 6 7 | х 9) и
о2= (х х 2 | 1 8 7 6 | 9 3).
Напоследок, первый "х" из потомка о1 (который должен был быть 1, но был обнаружен конфликт) заменяется на 4 (см. серию преобразований данных). Таким же образом, второй "х" из потомка о1 меняем на 5 и "х"-ы в потомке о2 меняем на 1 и 8 соответственно. Имеем потомков:
о1= (4 2 3 | 4 5 6 7 | 5 9) и
о2= (1 8 2 | 1 8 7 6 | 9 3).
PMX разрабатывает важные общности в значениях и порядке следования, кода используется с соответствующим образом разработанным воспроизводственным планом.
ОХ - строит потомков, выбирая кусок из одного родителя, остальные города - из другого, соблюдая очередность городов. Например, два родителя (разрезы отмечены " | ")
p1= (1 2 3 | 4 5 6 7 | 8 9) и
p2= (4 5 2 | 1 8 7 6 | 9 3)
могут получить потомков следующим способом. Во-первых, сегменты между точками обреза копируются потомкам (символом "Х" обозначается неизвестный символ).
о1= (х х х | 4 5 6 7 | х х) и
о2= (х х х | 1 8 7 6 | х х)
потом, начиная от второй точки обреза другого родителя, записываются оставшиеся города в том же порядке, в котором они были в родителях.
о1= (2 1 8 | 4 5 6 7 | 9 3) и
о2= (3 4 5 | 1 8 7 6 | 9 2).
Кроссовер ОХ использует свойство путевого представления, что порядок городов важен, а первый город - нет. Туры:
1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 и
2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 1
являются фактически идентичными.
СХ - строит потомков таким образом, что каждый город (и его позиция) приходят от одного из родителей. Вот как все происходит. Два родителя
p1= (1 2 3 4 5 6 7 8 9) и
p2= (4 5 2 1 8 7 6 9 3)
будут порождать первого потомка, взяв первый город от первого родителя:
о1=(1 х х х х х х х х).
После этого каждый город в потомке должен быть взят от одного из его родителей (с той же позиции, на которой находился предыдущий город в другом родителе). В нашем случае, это город 4. ставим его на ту же позицию, на которой он находился в р1
о1=(1 х х 4 х х х х х).
Далее действуя таким же образом, находим город 8, находящийся "ниже" города 4
о1=(1 х х 4 х х х 8 х).
Таким же образом ставим и города 3 и 2.
о1=(1 2 3 4 х х х 8 х).
Дальнейшее заполнение тем же образом невозможно, т.к. ниже города 2 находится город 1, т.е. образуется замкнутый цикл. Остальные города берем из другого родителя.
о1=(1 2 3 4 7 6 9 8 5).
Действуя таким же образом, но начиная с родителя р2, получим второго потомка
О2=(4 1 2 8 5 6 7 3 9).
СХ сохраняет абсолютную позицию элементов той же, что и у родителей.
Существуют и другие операции для путевого представления.
Путевое представление слишком бедное, чтобы представлять важные свойства тура, такие как ребра. Но по сравнению с другими векторными представлениями они показывают неплохие результаты, имеют достаточно широкие возможности.
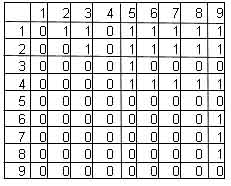
Фокс (Fox) и Макмахон (McMahon) тур как двоичную матрицу. В матрице элемент mij в строке i и столбце j содержит 1 если и только если город i стоит в туре перед городом j. Например, маршрут
(3 1 2 8 7 4 6 9 5)
представляется матрицей на рис.4.
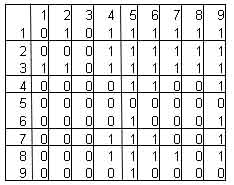
Рис.4. представление тура в виде матрицы.
В этом представлении, матрица М(n,n) представляющая тур (общий порядок городов) имеет следующие свойства:
Также количество единиц в каждом столбце (и в каждой строке) должны быть уникальными и Если количество единиц в матрице меньше, чем Операторы, используемые с таким представлением - пересечение и объединение. Обе операции - двоичные (кроссовероподобные операции). Как и для всех эволюционных программ, эти операции могут комбинировать особенности обоих родителей и сохранять ограничения одновременно.
Операция пересечения базируется на наблюдении, что пересечение бит от обоих родителей выдает матрицу, где количество 1-ц меньше, чем , и остальные два ограничения выполняются. Таким образом, мы можем дополнить матрицу, чтобы получить разрешенный тур. Например, два родителя
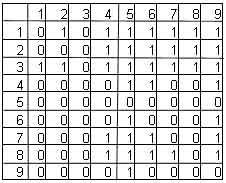
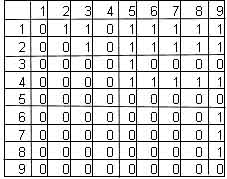
p1= (1 2 3 4 5 6 7 8 9) и
p2= (4 1 2 8 7 6 9 3 5)
представлены двумя матрицами (рис.5.)
Рис.5. два родителя
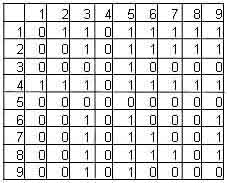
Рис.6. первая фаза операции пересечения.
В течение следующего стажа операции пересечения, один из родителей выбирается, несколько 1-ц (которые уникальны у этого родителя, "добавляются", и потом матрица заканчивается посредством анализа сумм столбцов и строк. Например, матрица на рис.5. может быть дополнена в течение следующего стажа до маршрута
(1 2 4 8 7 6 3 5 9)
Рис.7. окончательные результаты операции пересечения.
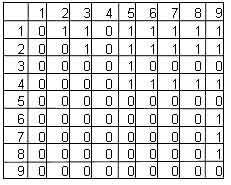
Операция объединения базируется на наблюдении, что подмножество битов от одной матрицы может быть безопасно комбинировано с подмножеством другой матрицы при условии, что пересечением двух матриц дает пустое пересечение. Оператор разделяет множество городов на две отдельные группы (для того, чтобы сделать это разделение, был создан специальный метод). Для первой группы городов он берет биты из первой матрицы, для второй группы - из второй матрицы. В конце он заканчивает матрицу, проанализировав сумму столбцов и строк и дополнив единицами (подобно операции пересечения).
Например, два родителя р1 и р2 и разделение городов на {1, 2, 3, 4} и {5, 6, 7, 8, 9} получат матрицу (рис.7.), которая заканчивается так же, как и для операции пересечения.
Рис. 8. первая фаза операции объединения.
Существует также представление, при котором в матрицу в элемент mij записывается 1 только в том случае, если i-й город непосредственно предшествует (является соседом, стоящим непосредственно перед) j-м городом.
Для всех представлений решения задачи коммивояжера справедливо следующее:
Количество минимальной популяции определяется по формуле:
Здесь n - количество городов, R - площадь квадрата, на котором эти города расположены, k- эмпирическая константа (приблизительно равна 0.765).
Одна из наиболее интересных проблем, которые можно решить с помощью ГА - проблема расписания.
Существует много версий проблемы расписания, одна из которых описана ниже. Существуют:
Задача состоит в том, чтобы составить оптимальное расписание (учителя - часы - классы- занятия); при этом должны быть полностью удовлетворены следующие условия:
Наиболее естественным было бы представление хромосомы потенциального решения проблемы расписания в виде матричного представления: матрица R(i,j) (1<=i<=m, и 1<=j<=n), где каждая строка соответствует учителю, а каждый столбец - часу; элементы матрицы - классы (rijЄ {C1, … , Ck}). Также возможно представление в виде трехмерной матрицы R(m,n,2), где элементы 1-го слоя матрицы - классы, элементы второго слоя - занятия.
Для такого представления были разработаны операторы:
В настоящее время генетические алгоритмы в нашей стране, да и за рубежом представляют собой перспективную, но малоизвестную область. В нашей стране практически нет книг на эту тему. Некоторые публикации - вот все, что можно найти. За рубежом, конечно, с этим полегче. Но работа с зарубежными материалами встречается с известными сложностями: доставка, трудность при незнании иностранных языков.
Использование генетических алгоритмов в решении комбинаторных задач дадут большую выгоду как в использовании вычислительных возможностей ЭВМ, так и вообще в возможности программного решения некоторых задач.
Цель работы и решаемые в ней задачи
Цель работы состоит в том, чтобы практически реализовать теорию генетических алгоритмов и получить программы, реально использующие их; сравнить результаты, скорость работы с другими программами, использующими генетические алгоритмы, а также использующими стандартные методы нахождения оптимума.
Ожидаемыми результатами являются рабочие программы, использующие генетические алгоритмы, представляющие отчет о затраченном времени на решение задачи, а также само решение задачи.
Степень новизны результатов: такая тема в Донецке исследовалась очень мало, в настоящее время ее исследование начало разворачиваться, раньше же эта тема была здесь неизвестна.
В магистерской работе планируется представить программы, реализующие решение задачи коммивояжера, составление расписания.
В настоящее время мною ведется работа над программой составления расписания с помощью генетических алгоритмов.
![]() , такой тур не является неправильным, он недоделанный. Для завершения его необходимо дополнить.
, такой тур не является неправильным, он недоделанный. Для завершения его необходимо дополнить.
![]()
Назад на главную страницу