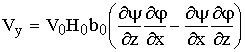• Биография
• Аннотированные ссылки
• Отчет о результатах поиска

 

Донецкий национальный технический университет

Нефедьев Александр Сергеевич

"Исследование формоизменения прямоугольной полосы

в двухэлементных калибрах"

 

Автореферат магистерской выпускной работы

Руководитель: проф. Бейгельзимер Я.Е.

Донецк, 2002

e-mail nefediev@ewarist.donetsk.ua

---

Исследование формоизменения прямоугольной полосы в двухэлементных калибрах

Предлагается довольно универсальный метод теоретического исследования прокатки в калибрах и описывается разработанная на его основе программа расчета прокатки. В качестве примера работы программы выполнен численный эксперимент и получены регрессионные соотношения для расчета параметров процесса прокатки в двухручьевых ромбических калибрах.  Сопоставление теоретических оценок с экспериментом показывается приемлемую, для практики, точность расчета основных параметров прокатки 

Введение

Наибольшие перспективы для теоретического исследования прокатки в калибрах открывают методы конечных (МКЭ)  и граничных (МГЭ)  элементов [1-4]. Достоинством этих методов является возможность решения задач объемного пластического течения для сложных очагов деформации с учетом реальных реологических свойств металла. Однако в настоящее время МКЭ и МГЭ пока еще нельзя рассматривать как наиболее эффективный инструмент для решения  всех задач пластического течения в калибрах. Анализ работ в области расчета трехмерных процессов ОМД показал [4], что применение существующих разработок, в том числе и дорогостоящих коммерческих программных продуктов, не удовлетворяет запросы промышленности по достоверности результатов расчета, уровню автоматизации подготовки данных и охвату актуальных задач производства. Отсутствует обоснование используемых подходов в части моделирования трехмерного течения несжимаемой нелинейно-вязко-пластической среды, недостаточно развиты методы учета граничных условий и реологических свойств металла.

По указанным причинам пока что актуальным является приближенный расчет прокатки, выполненный сравнительно простыми средствами. Речь идет о прикладных программах, стоимость и требуемое время расчета у которых в сотни раз меньше, чем у пакетов МКЭ. При меньшей, чем у пакетов МКЭ, точности вычислений, эти программы должны верно ориентировать технолога в выборе основных параметров прокатки.  При этом они должны быть универсальными, т.е. позволять исследовать калибры различных профилей.

В настоящей статье предлагается довольно универсальный метод теоретического исследования прокатки в калибрах и описывается разработанная на его основе программа расчета прокатки. В качестве примера работы программы и «работы с программой» выполнен численный эксперимент и получены регрессионные соотношения для расчета параметров процесса прокатки в двухручьевых ромбических калибрах.   

Постановка задачи прокатки в калибрах

Согласно [5], постановка задачи прокатки, с учетом свободного формоизменения, имеет вид:

найти поле скоростей и поверхность полосы, обеспечивающие минимум функционала полной мощности

 

                                                        (1)

где - интенсивность скорости деформации металла;

       - сопротивление деформации металла; - компоненты напряжения трения на поверхности S_k контакта полосы с валками; V_i – компоненты вектора скорости металла;   и  - соответственно скорость полосы на входе и выходе из калибра;  и   - соответственно силы, действующие на полосу, на входе и выходе из калибра (см.рис.1). 

Кинематически-возможное поле скоростей должно удовлетворять следующим условиям:

1.                 Условию несжимаемости

;                                                (2)

2.                 Граничным условиям:

2.1.          на поверхности  S_k нормальная к поверхности составляющая скорости металла должна равняться 0 (так называемое условие непроницаемости поверхности валков) (см.рис.1);

2.2.          в сечении полосы на входе в очаг деформации (S₀): ,  (см. рис.1);

 2.3.в сечении полосы на выходе из очага деформации (S₁): ,  (см. рис.1);

 

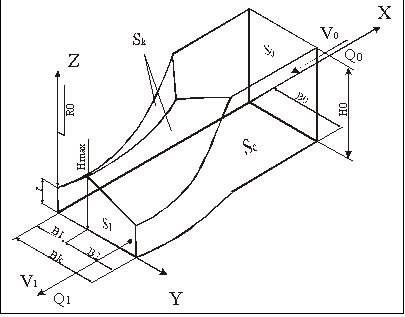
Рис.1-Элемент очага деформации при прокатке в калибре

S_k - поверхность контакта полосы с валком; S_с – свободная поверхность полосы; S₀ – «входное» сечение очага деформации; S₁ –«выходное» сечение очага деформации; V₀- скорость метала на входе в очаг деформации; V₁- скорость метала на выходе из очага деформации.

В работе [5] отмечается, что для действительного поля скоростей, являющегося решением задачи прокатки, функционал (1) равен нулю.

Основная проблема состоит в том, чтобы записать общее выражение для кинематически-возможного поля скоростей, содержащее варьируемые параметры. В разных работах эта проблема решается по-разному. В одних, условие несжимаемости удовлетворяется приближенно с помощью метода штрафных функций; в других, условие несжимаемости удовлетворяется точно, но условие непроницаемости поверхности валков не выполняется. На наш взгляд это вносит значительные погрешности, так как, по сути, решается другая задача, т.е. исследуется течение через калибр, не соответствующий заданному профилю.

В работе [6] конструируются поля скоростей, удовлетворяющие обоим условиям, но для этого калибр разделяется на простые элементы, в каждом элементе строится свое поле, на границах между элементами «сшиваются» нормальные к поверхности раздела компоненты поля, при этом касательные компоненты поля испытывают разрывы. Этот метод трудно алгоритмизировать так, чтобы вычислительная машина автоматически строила поле по заданному калибру.

 В следующем разделе изложен предлагаемый нами общий подход к построению непрерывного кинематически-возможного поля скоростей металла при прокатке в калибрах, который легко алгоритмизируется.

Кинематика пластического течения при прокатке прямоугольной полосы в калибрах

Подход включает в себя два этапа. На первом, записывается соотношение для поля скоростей, удовлетворяющее условию несжимаемости и содержащее две произвольные функции; на втором, эти функции определяются из условия непроницаемости поверхности валков и граничных условий во «входном» и «выходном» сечениях полосы.

Последовательно рассмотрим оба этапа.

Для математического описания стационарного течения металла при прокатке используется понятия линий и поверхностей тока [7].

Линиями тока называются линии, вдоль которых движутся частицы сплошной среды (в нашем случае – металла). В каждой точке линии тока, вектор скорости частицы направлен по касательной к этой линии (см. линия ab на рис.2; стрелками показан вектор скорости).

                   a)                                                              b)

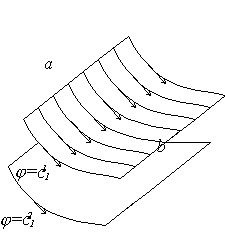
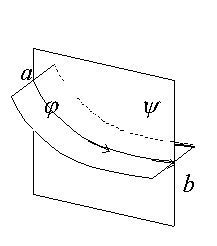
Рис.2 Линии и поверхности тока.

         a)поверхности тока j = const, образованные линиями тока;

b)линия тока ав , образованная пересечением двух поверхностей тока

j = const, и y = const.

 

Поверхностью тока называется поверхность, образованная линиями тока (см.рис.2а). Как и любая поверхность в трехмерном пространстве, поверхность тока задается уравнением j(x,y,z)=const. Функция j(x,y,z) называется функцией тока.

Изменяя величину константы в приведенном выше соотношении будем получать разные поверхности тока, принадлежащие одной системе поверхностей тока (см.рис.2а, поверхности j(x,y,z)=С¹₁ и j(x,y,z)=С²₁).

Для описания пластического течения металла удобно ввести две системы поверхностей тока. При этом линию тока можно представить как пересечение двух поверхностей, принадлежащих разным системам (на рис.2b эти системы поверхностей обозначены буквами j  и y).

Системы поверхностей тока задают уравнениями

j (x,y,z)=C₁ и y (x,y,z)=C₂    ,                             (3)

где С₁ и С₂ – постоянные, фиксирующие определенные поверхности тока в разных системах; j(x,y,z) и y (x,y,z)- функции тока.

Поле скоростей металла определяется через функции тока в следующем виде [7]:

                                                            (4)

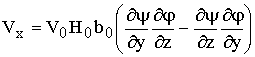
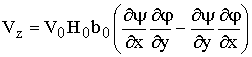
где x,y,z - координаты, соответственно, вдоль направления прокатки, по ширине и по высоте полосы; V₀ - скорость полосы на входе в калибр, 2H₀ - начальная толщина полосы, 2b₀ – начальная ширина полосы;

Для того чтобы это поле было кинематически возможным, необходимо, путём выбора функций  и , добиться выполнения условий непроницаемости поверхности валков и стыковки с жесткими концами полосы. При этом функции  и  должны содержать варьируемые параметры, величина которых определяется из дополнительных условий

Так как частицы металла движутся вдоль поверхностей тока, то последние являются  «непроницаемыми» для этих частиц. Мысленно представим себе канал, стенками которого являются поверхности тока. Частицы металла, движущиеся внутри этого канала, никогда не смогут выйти за его пределы по причине непроницаемости его стенок. Ясно, что прокатываемая полоса как раз и представляет собой такой канал, а ее поверхности являются поверхностями тока (см.рис.1).

Запишем функцию тока y в виде:

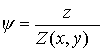,                                                               (5)

где Z(x,y)- уравнение поверхности, нигде не пересекающей валки, а на участках контакта с ними, совпадающей с их поверхностью.

Из соотношения (5) следует, что на поверхности, задаваемой уравнением z=Z(x,y), функция тока y=1. Это означает, что эта поверхность является поверхностью тока и нормальная к ней составляющая скорости металла равняется нулю. Отсюда сразу же получаем, что принимая  y  в виде (5) мы удовлетворяем условию непроницаемости поверхности валков, а уравнение z=Z(x,y) задает при этом кинематически-возможную поверхность полосы.

Выражение для второй функции тока примем в следующем виде

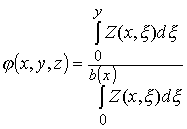,                                                          (6)

где b(x)- координата боковой поверхности полосы.

Непосредственная подстановка (5) и (6) в соотношения (4) показывает, что принятое соотношение для j обеспечивает выполнение условия стыковки с жесткими концами полосы.

Боковая поверхность полосы описывается следующим соотношением

,                                                  (7)

где - отношение текущей ширины полосы к ширине исходной полосы; -отношение координаты x к длине очага деформации; 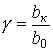 – коэффициент уширения; - ширина полосы после прокатки.

Последнее соотношение задает плавный переход от исходной полосы с шириной , к конечной полосе, с шириной . Коэффициент  уширения является параметром, величина которого определяется путем минимизации функционала полной мощности.

Основная проблема при построении описанной выше структуры состоит в том, что, как правило, трудно записать подходящее соотношение для Z(x,y), так как калибр может иметь сложную конфигурацию. Указанная проблема достаточно просто решается путем привлечения аппарата теории R-функций, который был разработан с целью получения уравнений границ для областей сложной формы [8].

Согласно [8] для того, чтобы получить уравнение границы сложной области, ее, прежде всего, представляют в виде объединения и  пересечения относительно простых областей, границы которых  можно записать в аналитическом виде. Этот факт записывают в виде математического соотношения, в котором области отображаются значками, а их объединения и пересечения - предикатами алгебры логики.  После этого указанные значки заменяют так называемыми функциями формы областей, а предикаты алгебры логики – R-функциями. Функции формы обладают следующими свойствами: на границе области ; внутри области ; вне области .

Имеются различные классы  R-функций, каждый из которых обеспечивает ту либо иную степень гладкости сопряжения в угловых точках области. Например (см.[8]):

класс R₀

      ,                  (8)

                         (9)

класс R₁

,                           (10)

         .                  (11)

где  – R-функция, которая ставится вместо знака , указывающего на пересечение областей с функциями формы , ;  – R-функция, которая ставится вместо знака , указывающего на объединение областей с функциями формы ,.

Класс  R₀ обеспечивает гладкое сопряжение участков границы в угловых точках; класс  R₁ не сглаживает угловых точек.

Непосредственными вычислениями легко показать, что при использовании R₁-функций и задании функций формы простых областей в виде

w_i(x,y,z)= Z_i(x,y)-z,                                                                (12)

суммарная функция формы также имеет вид

w(x,y,z)= Z(x,y)-z                                                                  (13)

Из последнего соотношения получаем

Z(x,y)= w(x,y,0)                                                            (14)

Это позволяет конструировать уравнения поверхностей полосы для различных калибров.

Действительно, прокатываемую полосу можно представить в виде области, объединяющей полосу до и после прокатки, которая пересекается областью, лежащей вне тела валков [9]. Для каждой из этих областей легко записать уравнения функции формы в виде (12). После чего, с помощью соотношений (10)-(11), записывается функция формы всей полосы, а соотношение (14) позволяет получить уравнение поверхности полосы. При этом легко учесть возможное не заполнение калибра (см. [9]) и ввести в  Z(x,y) параметры, его характеризующие. Эти параметры, также как и коэффициент уширения, определяются путем минимизации функционала мощности.

Особенности вычислительных алгоритмов

Использование приведенных выше соотношений  связано с выполнением действий одно- и двукратного численного дифференцирования (одного для получения скоростей и второго для получения скоростей деформаций) и численного интегрирования. Основные проблемы при численном дифференцировании возникают на границах очага деформации, представляющего сложную область. Решение этих проблем возможно путем перехода в криволинейную систему координат , в которой очаг деформации имеет вид куба с единичным ребром. Такое преобразование координат определяется следующими соотношениями:

                                                                     (15)

                                               (16)

В наших алгоритмах мы использовали формулы [10] численного дифференцирования со сглаживанием квадратичными параболами. Они дают устойчивые результаты при двукратном дифференцировании.

Минимизация функционала мощности осуществляется методом золотого сечения.

На основе изложенной выше методики разработана программа на языке Delphi 5.0, которая позволяет рассчитывать следующие характеристики и параметры прокатки в калибре: коэффициент уширения; коэффициент, характеризующий не заполнение профиля; поле скоростей течения металла; искажения координатных сеток; энергосиловые параметры. В качестве исходных данных для расчета задаются: контур калибра,  предел текучести металла, коэффициент контактного трения, максимальный радиус валков, высота и ширина полосы. Контур калибра может задаваться в следующем виде: уравнений отдельных участков контура; таблицы с координатами достаточно большого числа точек, лежащих на контуре; графического файла из пакета AutoCAD.  

В следующем разделе приведен пример расчета, выполненного с помощью разработанной программы.

Расчет процесса прокатки в двухручьевых ромбических калибрах

В последнее время получила широкое распространение двухручьевая прокатка-разделение, технология которой заключается в формировании сечения профиля, состоящего из двух простых элементов (например, квадратов), соединенных относительно тонкой перемычкой, с последующим разделением этого сечения по перемычке в прокатных валках или специальных кассетах.

Формирование профиля происходит в специальном формирующем калибре, профиль которого показан на рис.3

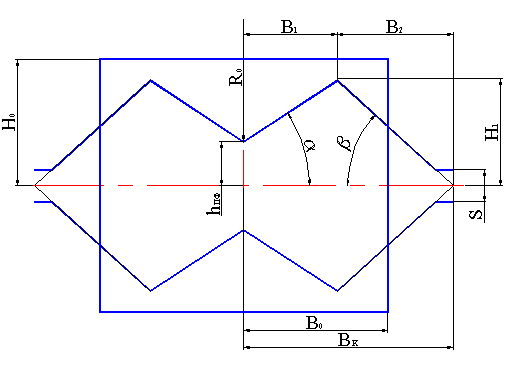
Рис.3 – Профиль формирующего двухручьевого калибра и входящей в него заготовки прямоугольного сечения

Исходные данные для расчета следующие:

H₀ – высота заготовки;

B₀ – ширина заготовки;

B₁ – расстояние от перемычки до вершины калибра;

B₂ – расстояние от вершины калибра до скелетной точки;

B_К – ширина калибра по скелету;

h_ПФ – высота перемычки;

H₁ – высота калибра;

R₀ – радиус валка;

f_у..- коэффициент контактного трения.

Углы a и b рассчитываются по исходным данным.

В Таблице 1 приведены результаты расчета в сопоставлении с экспериментом. Последние четыре колонки этой таблицы показывают, что разработанное математическое и программное обеспечение позволяет с вполне приемлемой степенью точности определить основные параметры прокатки в двухручьевых ромбических калибрах.

На основе численного эксперимента и обработки его результатов с помощью пакета STATISTICA 5.5 получены следующие регрессионные соотношения для основных параметров процесса прокатки в двухручьевых формирующих калибрах:

для коэффициента уширения

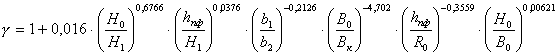  (17)

R²=0,987

 для коэффициента вытяжки

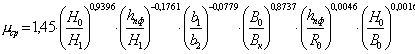                                 (18)

R²=0,999

для коэффициента относительного незаполнения калибра по высоте

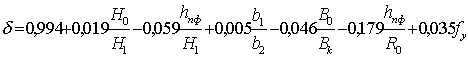                    (19)

R²=0,876

для относительной мощности прокатки ()

            (20)

R²=0,92

для коэффициента плеча момента прокатки

                                                                 (21)

R²=0,803

Эти соотношения могут использоваться при проектировании двухручьевых ромбических калибров.

 

Библиографический список

1.     Mori K., Osakada K. Simulation of the Tree Dimensional Rolling by the Rigid-Plastic Finite Element Method// Numerical methods in industrial forming processes, Pineridge Press, Swansea, UK 1982.- P. 747-756

2.     Yanagimoto J., Kiuchi M., Three –dimensional Rigid-Plastic FE Simulation System for Shape Rolling with Inter-Stand Remeshing// Metall Forming Processes Simulation in Industry, 28-30 September, 1994, Baden-Baden, Germany, P. 221-237.

3.     Миленин А.А. Исследование с помощью математической модели процесса уширения при прокатке металлов с разными реологическими свойствами/ Металлы.-1998.-№4.-С.48-51.

4.     Миленин А.А. Разработка научных основ и развитие технологий трехмерного пластического формоизменения металлов с применением методов компьютерного моделирования. Автореф. дисс.д.т.н. Днепропетровск, 2001.-35 с.

5.     Колмогоров В.Л., Смирнов В.К. Применение функционала типа функционала Маркова для решения задач продольной прокатки/ В кн. Обработка металлов давлением. Межвузовский сборник научных трудов. Свердловск: УПИ, 1976.-С.41-45

6.     Тарновский И.Я., Скороходов А.Н., Илюкович Б.М. Элементы теории прокатки сложных профилей М.: Металлургия, 1972.-352 с.

7.     Гун Г.Я. Математическое моделирование процессов обработки металлов давлением. Учебное пособие для вузов. М., "Металлургия", 1983. 352 с.

8.     Рвачев В.Л. Теория R-функций и некоторые ее приложения. К.: Наукова думка, 1982.- 551с.

9.     Компьютерное моделирование объёмного пластического течения металла при прокатке в калибрах/В.А.Нечепоренко, А.Г.Маншилин, Г.М.Шульгин, Я.Е.Бейгельзимер, А.В.Спусканюк// Сталь, №6, 1999, с. 38-42

10. Ланцош К. Практические методы прикладного анализа. -М.: Гос. изд-во физ.-мат. литературы, 1961.-524 с.

 

 

 

 

 

 

 

Таблица 1 – Сопоставление результатов расчета по математической модели и результатов эксперимента