|
|
Автореферат
Тема диссертации: MIMD-модель сетевого объекта с сосредоточенными
параметрами
Руководитель: проф.Святный В.А.
Факультет: ФВТИ
Специальность: "Комьютерные интелектуальные системы и сети"
Общая характеристика работы
Содержание работы
Основные результаты
Список литературы
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы:
Моделирование динамических систем с сосредоточенными параметрами (ДССП) является актуальной проблемой для всех
областей техники и технологий. В последние годы методы и средства моделирования интенсивно используются в реальных
технических и технологических проектах для проверки правильности проектных решений и выступают тем самым как
важнейший фактор, гарантирующий качество проектирования, сокращение сроков внедрения проектов и освоения управляемых
динамических систем обслуживающим персоналом. Играя столь важную роль в техническом и технологическом прогрессе,
моделирование как метод исследования выдвигает ряд требований к вычислительным системам и их программному обеспечению
как средствам реализации моделей. Анализ показывает, что для построения массивно параллельной моделирующей среды
(ПМС) широко используют MIMD-компоненту. Представляет интерес разработка MIMD-моделей сетевого объекта (СО) с
сосредоточенными параметрами.
Цель и задачи исследования:
Целью данной работы является разработка, отладка и экспериментальные исследования MIMD-модели, ориентированной на
решение задач моделирования шахтных вентиляционных сетей (ШВС), которые рассматриваются как динамические объекты с
сосредоточенными параметрами.
В работе решаются следующие задачи:
1.Характеристика MIMD-модели сетевого объекта с сосредоточенными параметрами.
2.Рассмотрение современных методов моделирования динамических систем, формулирование требований динамических систем
к средствам их моделирования.
3.Разработка структуры MIMD-модели СО.
4.Разработка алгоритмов топологического анализатора, генератора и решателя уравнений для MIMD-компоненты ПМС.
В процессе создания MIMD-модели СО использовалась теория графов, численные методы решения дифференциальных
уравнений, методы параллельного программирования для MIMD-архитектур, экспериментальная проверка программ
последовательных и параллельных алгоритмов моделирования на тестовых ШВС.
Научная новизна:
1.Предложенная MIMD-модель является новой формой системной организации средств моделирования сетевых динамических
систем с сосредоточенными параметрами и открывает позитивные перспективы эффективного использования параллельных
вычислительных ресурсов, основанных на MIMD-организации, для комплексного решения задач моделирования ШВС.
2.Предложены алгоритмы работы топологического анализа для формирования и решения уравнений сетевого динамического
объекта с сосредоточенными параметрами, отличающиеся пошаговым преобразованием таблицы кодирования графа и
интеграцией с алгоритмами.
3.Экспериментально подтверждена работоспособность алгоритмов топологического анализа, формирования и решения
уравнений для сетей различной сложности.
Практическое значение и реализация полученных результатов:
Работа относится к проблематике кафедры ЭВМ, решаемой в рамках государственной программы разработки конкурентно
способных средств моделирования сложных систем и договорах о научном сотрудничестве с Штутгартским университетом
по разработке параллельной моделирующей среды.
СОДЕРЖАНИЕ РАБОТЫ
В главе 1 определяется понятие сложной динамической системы (СДС) и их использования в различных
областях науки и техники. Анализируются требования к математическим моделям, которыми описываются сложные сети и
их системы управления. Дана краткая характеристика аэродинамическим, электрическим, гидравлическим сетям, как
представителям сетевых динамических объектам. Определяются задачи моделирования сетевых объектов:
-естественное и управляемое воздухораспределение;
-исследование газодинамических процессов;
-поиск аэродинамических сопротивлений при заданном воздухораспределении;
-исследование и сопровождаемое моделями проектирование систем автоматизации проветривания шахт;
-моделирование критически опасных ситуаций и разработка мероприятия по их устранению.
В главе 2 разработана структура MIMD-модели сетевого объекта
Дано краткое описание блоков алгоритмической структуры модели:
Топологический анализатор (ТА) - аппаратно-программные средства, обеспечивающие удобное описание топологии на
некотором входном языке (формально-вербальном), кодирование топологии, формирование описаний топологий, по которым
могут быть составлены уравнения протекания процессов.
Генератор уравнений (ГУ) - программное средство, которое по данным ТА и по уравнениям элементов СО формирует
систему уравнений всей динамической системы в целом. Генератор уравнений выполняет матрично-векторные операции,
соответствующие переходу от одной системы уравнений к другой, удобную для численного решения.
Решатель уравнений (РУ) - аппаратно-программное средство, которое реализует некоторый численный метод решения
сформированных уравнений. РУ включает блок инициализации (ввод параметров из файла, задание векторов начальных
условий Y(0), блок цикла с управлением по точности или по заданному времени интегрирования и блок визуализации.
Визуализация результатов моделирования (ВРМ) - представляет собой средства компьютерной графики, с помощью
которых в наглядной форме представляются результаты моделирования.
Подсистема диалога - программное средство, обеспечивающее для пользователя "доброжелательный" интерфейс со
всеми функциональными блоками модели СО.
В главе 3 разработан MIMD-ориентированный топологический анализатор, дано его определение и
функции:
- кодирование топологии сетевого объекта в форме задания связей,
параметров и вербального описания ветвей, которые важны для этой
предметной области.
- построение дерева и антидерева графа сетевого объекта.
- перекодирование топологии в соответствии с выбранным вариантом
дерева и антидерева.
- построение топологических матриц инциденций A и независимых
контуров S.
Приведена структура топологического анализатора:
Разработан табличный метод топологического анализатора.
В главе 4 разработан MIMD-генератор уравнений.
Для составления модели сетевого объекта с сосредоточенными параметрами важную роль играет генератор уравнений.
Метод формального преобразования топологических матриц уравнений дает хорошую возможность для формирования
сетевой модели. Система уравнений аэродинамической сети представляется в следующем виде:
вид которой является удобным для решения численными методами [1], где TP=(SyKy - SxKxW)-1*S, RU=(SyKy - SxKxW)-1*SR,
W=Ax-1Ay.
Алгоритм генерирования этих систем выражается с помощью операций над матрицами Ax, Ay, Sx, Sy, Kx, Ky, Rx, Ry, S, R.
Компоненты векторов H(Hx(X), Hy(Y)) являются функциями динамических процессов, которые вычисляются в итерационном
цикле решателя уравнений. Поэтому результатом генерации уравнений являются топологическая и параметрическая матрицы:
TP=(SyKy - SxKxW)-1S,
RU=TP*R=(SyKy - SxKxW)-1S*R;
TP=(SyLy - SxLxW)-1S,
RU=TP*R=(SyLy - SxLxW)-1S*R.
Генератор уравнений сетевого объекта реализуется в параллельных MIMD-системах. В MIMD-компоненте моделирующей
среды алгоритмы реализованы на языке С при MPI-организации обмена между процессами.
В главе 5 рассматривается решатель уравнений. Решатель уравнений должен представлять собой
программу, реализующую циклический алгоритм численного решения матрично-векторных систем уравнений. Воспользуемся
численным методом Адамса-Бошфорта, который реализован в существующих последовательных языках моделирования.
Сделаем попытку унифицировать процессы решателя уравнений в дополнение к тому, что они структурированы
матрично-векторной формой записи.
По-видимому, есть смысл этот этап делать в таком порядке:
- схема решателя
- анализ подходов к распараллеливанию программы РУ
- расcмотрение SPMD - принципа
- организация связи между процессами
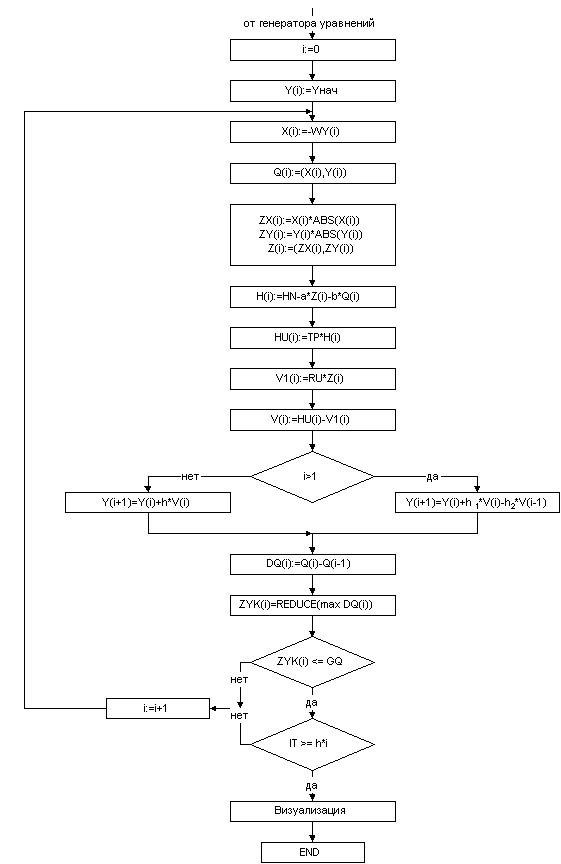
Схема решателя уравнений.
Составим блок-схему обычной последовательной программы, имея в виду матрично-векторные операции:
ОСНОВНЫЕ РЕЗУЛЬТАТЫ
1. Дано определение MIMD-модели сетевого объекта с сосредоточенными параметрами.
2. Сформированы требования к динамическим системам и к способам их моделирования.
3. Разработана, имплементована и отлажена основная компонента РПМС - решатель уравнений.
Выводы: дано определение MIMD-модели сетевого динамического объекта, которое
аккумулирует опыт моделирования в определенных областях науки и техники, сформированы требования динамических
систем к способам их моделирования в MIMD-компоненте РПМС.
ЛИТЕРАТУРА
1. Абрамов Ф.А., Фельдман Л.П., Святный В.А. Моделирование динамических процессов рудничной аэрологии. Киев,
Наукова думка, 1981, 291 с.
2. Цой С., Цхай С.М. Прикладная теория графов. - Алма-Ата: Наука, 1971, 500 с..
3. Святний В.А. Проблеми паралельного моделювання складних динамічних систем. Наукові праці ДонДТУ, Серія ІКОТ,
вип. 6., 1999, с. 6-14.
Общая характеристика работы
Содержание работы
Основные результаты
Список литературы
|
|
|
