Develop: технический журнал Apple (Выпуск
№25)
NURB-кривые: руководство для непосвященных
QuickDraw 3D поддерживает математическую модель для произвольных
кривых и поверхностей, известных как NURB (nonuniform rational B-splines
– неравномерные рациональные B-сплайны). NURB кривые являются гибкими
и мощными, но их эффективное использование требует некоторого понимания
лежащей в их основе математической теории. Данная статья представляет
наглядное введение в математические идеи NURB-моделей и того, как
использовать их в ваших программах для QuickDraw 3D.
Одной из наиболее мощных возможностей QuickDraw 3D является ее
возможность работать с кривыми и поверхностями произвольной формы.
Математическая модель, которую он использует, известна как NURB,
т.е. неравномерные рациональные B-сплайны. Модель NURB гибка и мощна,
но для тех, кто не знаком с математикой, она может показаться устрашающе
сложной. Существующие книги и статьи на данную тему склонны быть
точными, многословными и умозрительными, и часто подразумевают,
что вы уже знаете предмет, чтобы понять изложенное.
Однако математика не так устрашающа, если вы ее понимаете. Цель
данной статьи – дать вам наглядное понимание того, как работают
кривые NURB. Далее в статье мы рассмотрим код, чтобы показать вам
как вы можете начать использовать кривые NURB в ваших собственных
программах. Но вам в действительности нужно понять теорию до того,
как вы сможете применить ее на практике. Поэтому, пожалуйста, будьте
терпеливы пока мы будем пробираться через математические понятия:
обещаю, что мы подойдем к действительному программированию до того
как пройдем все. Заметьте также, что эта статься не только о кривых
NURB; возможно будущая статься будет посвящена NURB-поверхностям
и тому, как использовать кривые и поверхности вместе.
Некоторые авторы также используют s от "spline" для
получения акронима NURBS. Но большинство избегает его использование,
потому что фраза вроде "a NURBS curve" звучит ужасно,
а "a NURBS surface" звучит просто отвратительно.*
Почему NURB кривые?
Как любые графические пакеты, QuickDraw 3D предлагает низкоуровневые
графические примитивы для объектов, таких как линии, точки, треугольники.
Потому что представления этих объектов математически точны – линии
определяются двумя концами, треугольники своими тремя вершинами,
и так далее – они растрово независимы, и не зависят от позиции,
масштаба и ориентации.
Низкоуровневые примитивы могут быть также использованы для определения
объектов произвольной формы, таких как футбольный мяч или капот
автомобиля, но за цену этих желаемых математических свойств; например,
окружность, аппроксимированная последовательностью отрезков линии,
изменит свою форму во время вращения. Одно из преимуществ NURB-кривых
это то, что они предлагают путь представления произвольных форм
одновременно математически точных и растрово независимых. Среди
этих полезных свойств следующие:
- они могут представлять поистине любую желаемую форму, от точки,
прямой линии и ломаной до конических отрезков (окружностей, эллипсов,
парабол и гипербол), кривых произвольной формы;
- они дают вам большой контроль над формой кривой. Набор контрольных
точек и узлов, которые направляют форму кривой, ими можно непосредственно
манипулировать, чтобы управлять их гладкостью и кривизной;
- они могут представлять очень сложные формы с относительно малым
набором данных. Например, аппроксимация окружности трех футов
в ширину последовательностью отрезков прямой потребует десятки
тысяч сегментов, чтобы она выглядела как окружность, а не многоугольник.
Определение той же окружности с помощью NURB-представления потребует
лишь семи управляющих точек.
В дополнение к рисованию NURB-кривых непосредственно как графических
элементов, Вы можете использовать их в других различных направлениях,
которые используют их полезные математические свойства, такие как
направляющие пути анимации или для интерполяции или приближения
данных. Вы можете также использовать их как инструмент, чтобы проектировать
и управлять формами трехмерных поверхностей, для целей типа:
- поверхности кругового вращения (двумерной кривой вокруг оси
в трехмерном пространстве)
- выдавливание (перенос кривой по изогнутому пути)
- обрезка (срезание части NURB поверхности, используя кривые NURB,
чтобы определить вырезку)
КРИВЫЕ 101
Прежде, чем мы вникнем в специфику кривых NURB, давайте сделаем
обзор некоторых основ представления кривой вообще.
Хотя QuickDraw трехмерные поддерживает трехмерные кривые NURB, мы
ограничим все наши примеры и обсуждения здесь к двум измерениям.
Но все, что мы говорим о двумерных кривых, применяется аналогично
в трех измерениях - двумерные версии просто проще визуализировать
и проще рисовать.
Немного ИСТОРИИ
В докомпьютерные времена архитекторы, инженеры и художники рисовали
бы проекты зданий, дорог, частей машин, и т.п., используя карандаш,
бумагу, и различные черновые инструментальные средства. Эти инструментальные
средства включили линейки, и рейсшины (наугольники) для черчения
кругов и круговых дуг, треугольников и транспортиров для образования
точных углов.
Конечно, много объектов, имеющих интересную форму, не могли быть
начерчены только с этими простыми инструментальными средствами,
потому что у них были изогнутые части, которые не были просто окружностями
или эллипсами. Часто была необходима кривая , которая гладко проходит
через множество предопределенных точек. Эта проблема была особенно
остра в судостроении: хотя квалифицированный художник или чертежник
могли такие кривые надежно рисовать рукой на чертежном столе, судостроителям
часто необходимо было делать чертежи в натуральную величину (или
почти в натуральную величину), где абсолютный размер требуемой кривой
нарисовать вручную было невозможно. Из-за их большого размера, такие
рисунки часто сделались в области чердака большого здания специалистом,
известным как чердачник (loftsman). В качестве вспомогательного
средства чердачник использовал в задаче длинные, тонкие, гибкие
полосы древесины, пластмассы, или металлический, называемый сплайнами.
Сплайны поддерживались в месте с ведущими весами, называемыми утками
из-за их подобия крылатому созданию с тем же самым названием (см.
рисунок 1).

Рисунок 1. Сплайн чертежника
Результирующие кривые были гладкими, и изменялись по искривленности
в зависимости от позиции уток. Поскольку компьютеры вошли в употребление
в процессе проектирования, физические свойства таких сплайнов были
исследованы, так что они могли быть смоделированы математически
на компьютере.
Наша цель состоит в том, чтобы математически точно представить
кривые. Один из простых путей состоит в том, чтобы представить кривую
как график функции:
y = f (x)
Возьмите простой график подобный тригонометрической функции синуса:
y = sin x
Составляя график значения функции для различных значений x и соединяя
их гладко, мы получаем кривую, показанную на рисунке 2.

Рисунок 2. График значений функции синус
В случае кривых, нарисованных сплайновым методом, оказалось, что
с некоторыми разумными предположениями упрощения, они могли быть
математически представлены рядом кубических (третий градус((третья
степень)) полиномов, каждое из которых имеет форму
y = Ax3 + Bx2 + Cx + D
В этой точке, стандартные рекомендации типично входят в длительное,
вовлеченное развитие этой идеи в то, что известно как кубические
сплайновые кривые, в конечном счете ведя к теории кривых NURB. Такие
объяснения интересны, но не ужасно интуитивны.
Если Вы заинтересованы продолжением этого предмета далее, Вы найдете
хорошее его рассмотрение в Mathematical Elements for Computer
Graphics (Математических элементах компьютерной графики).
(Полная информацию относительно этой и других литературных ссылок
в этой статье могут быть найдены в библиографии в конец.)
ПАРАМЕТРИЧЕСКИЕ ФУНКЦИИ
Использование прямых функций для представления кривой соответствует
нашему критерию математической точности, но это имеет один серьезный
недостаток: так как мы можем иметь только одно значение y для каждого
значения x, наши кривые не могут быть замкнутыми. Таким образом,
хотя мы можем таким образом делать несколько хороших гладких кривых,
есть множество интересных кривых, которые мы не можем делать - даже
что-то столь же простое как окружность.
Альтернативный способ, и тот, который мы будем использовать, состоят
в том, чтобы определить кривую с параметрической функцией.
Вообще, такие функции имеют вид
Q (t) = {X (t), Y (t)}
где X (t) и Y (t) - функции по параметру t (следовательно параметрические).
По значению t, функция X (t) дает соответствующее значение x, а
Y (t) - значение y. Один из способов понимания такие функции состоит
в том, чтобы вообразить частицу, путешествующую по листу бумаги
и вычерчивающую кривую. Если Вы представите t как время, то параметрическая
функция Q (t) дает {x, y} координаты частицы во время t. Например,
определения функции X (t) и Y (t) как
X (t) = cos t
Y (t) = sin t
дадут круг, как Вы можете проверять подстановкой некоторых значений
t между 0 и 2 [[pi]] и составляя график результатов.
ГЛАДКОСТЬ
Один очень важный мотив для использования NURB кривых - способность
управлять гладкостью. Модель NURB позволяет Вам определять кривые
без петель или внезапных изменений направления (таких как сечение
крыла самолета) или с точным контролем над тем, где встречаются
петли и изгибы (например, острые углы объектов машин).
Все мы знаем (или думаем, что знаем) что хорошая, гладкая кривая,
выглядит так, что она не имеет никаких петель или углов. Если бы
мы должны были находиться на той перемещающейся частице, как это
видно из параметрической кривой, мы бы испытали хорошую гладкую
поездку без остановки, перезапуска, или внезапных изменений в скорости
или направлении: мы бы двигались, скажем, север и затем сразу на
восток. Это интуитивное понятие может быть выражено в точных математических
терминах. Вообразите стрелку, которая всегда указывает в направлении,
в котором наша гипотетическая частица путешествует, когда перемещается
по кривой. Математически, стрелка направления соответствует тангенсу
кривой, которая может быть вычислена как производная функции, определяющей
кривую, по параметру времени t:
Q ' (t)
На рисунке 3, например, точка на кривой, соответствующей времени
tA, обозначена как Q (tA), и вектор направления (касательная) в
этой точке как Q' (tA). Если касательная не прыгает внезапно от
одного направления в другое, то говорят, что функция кривой имеет
непрерывность по первой производной (обозначается C1). Это соответствует
нашему интуитивному понятию гладкости.

Рисунок 3. Касательная (производная) к кривой
Теперь смотрите на точку, обозначенную Q (tB), где есть видимая
петля на кривой. Вектор направления, как крошечный кусочек линии
влево от точки, Q ' (tB-[[альфа]]), дико отличается от направления
крошечного кусочка линии вправо, Q ' (tB + [[альфа]]). Фактически,
вектор направления переходит мгновенно от одного направления до
другого в точке Q (tB). Математически, это называется разрывом.
Многие из Вас вспомнят из ваших исчислений в колледже, что производная
функции - также функция, степень которой на один меньше исходной.
Например, производная функции четвертой степени - функция третьей
степени. Производная производной, называемой второй производной,
будет тогда иметь степень 2. Эта вторая производная может быть,
а может и не быть непрерывной. Если это так, мы говорим, что первоначальная
функция имеет непрерывность по второй производной, или
C2. Поскольку первая производная описывает направление кривой, вторая
производная описывает, как быстро это направление меняется. Вторая
производная, таким образом, характеризует степень кривой искривления,
и поэтому кривая C2-непрерывна, как считают, имеет непрерывную
кривизну. Мы возвратимся к этим важным понятиям после того,
как мы представим собственно кривые NURB.
Теперь, когда мы знаем, как работает параметрическая функция, давайте
посмотрим, как мы можем их использовать, чтобы построить определение
для кривых NURB. Если мы называем нашу функцию Q, левая часть нашего
уравнения будет выглядеть следующим образом:
Q (t) =
где t - параметр, представляющий время. Оценивая эту функцию в
множестве значений t, мы получим ряд {x, y} пар, которые мы можем
использовать для составления графика нашей кривой, как показано
на рисунке 4. Теперь все, что мы должны делать - определяют правую
часть.

Рисунок 4. Вычерчивание параметрической функции
УПРАВЛЯЮЩИЕ ТОЧКИ
Одна из ключевых характеристик кривых NURB - то, что их форма определена
(среди других вещей) позициями набора точек называемых управляющими
точками, подобно тем, что обозначены как Bi на рисунке 5. Также
как на рисунке, контрольные точки часто соединены линиями, чтобы
их легко можно было увидеть и показать их отношение к кривой. Эти
соединительные линии формируют то, что известно управляющий
многоугольник. (Вообще-то, имело бы больший смысл назвать ее
"управляющей ломаной", но первое название является традиционным.)

Рисунок 5. Определение кривой с управляющими точками
Вторая кривая на рисунке 5 - это та же самая кривая, но с одной
немного смещенной контрольной точкой B7. Обратите внимание, что
форма кривой не изменяется по всей длине кривой, а только в маленьком
окружении контрольной точки. Это очень желательная свойство, так
как это позволяет нам делать локализированные изменения перемещением
отдельных контрольных точек, без не воздействуя на форму всей кривой.
Каждая контрольная точка влияет на близлежащую к ней часть кривой
и мало воздействует или вообще не воздействует на части кривой,
которые находятся дальше.
Чтобы понять это, представьте, как сильно влияет каждая управляющая
точка на путь нашей движущейся частицы в каждый момент времени.
В любое время t, позиция частицы будет взвешенным средним всех управляющих
точек, но ближние к частице точки несущей большее количество веса
чем те, что дальше. Мы можем выражать это интуитивное понятие математически
таким образом:

Другими словами, чтобы определить позицию перемещающейся частицы
в определенное время, сложите позиции всех контрольных точек (Bi),
но варьируйте силу воздействия каждой точки по времени (Ni, k (t)).
Мы вскоре поясним значение индекса k.
Ограничивающий объем, возвращаемый QuickDraw 3D, для всех других
геометрических примитивов является объемом, включающий собственно
примитив. Однако, для кривых NURB, возвращенный ограничивающий объем
включает контрольные точки кривой, а не саму кривую. Это сделано
по историческим причинам, и является обычной практикой в трехмерных
графических пакетах.*
БАЗИСНАЯ ФУНКЦИЯ
Функция Ni, k (t), который определяет, как сильно управляющая точка
Bi влияет на кривую во время t, называется базисной функцией для
этой контрольной точки. Фактически, B в "B-сплайнах" стоит
вместо "основание" ("basis"). Значение этой
функции - вещественное число типа 0.5, так, чтобы определенная точка
Q (t) могла быть определен, скажем, как 25 % позиции одной контрольной
точки, плюс 50 % другой, плюс еще и 25 % третей. Чтобы завершать
наше NURB уравнение, мы должны определить базисную функцию для каждой
контрольной точки.
Так как мы поступим с определением базисной функций? Помните, что
мы хотим, чтобы каждая область кривой NURB была локальным средним
из некоторого небольшого числа управляющих точек близких к этой
области. Когда движущаяся частица далеко от данной управляющей точки,
то эта управляющая точка не сильно влияет на нее; когда частица
становится ближе, управляющая точка воздействует на нее все больше.
Затем воздействие уменьшается снова, поскольку частица отступает
от управляющей точки.
До сих пор, мы использовали слова "около" и "далеко"
довольно неопределенным способом, но время прибыло определить их
более строго. Поскольку мы определили нашу кривую параметрически
относительно времени, мы можем расценивать то, что мы назвали "часть"
или "область" кривой как часть интервала времени покрытиями
кривой. Например, если наша кривая идет со времени t = 0.0 к t =
10.0, мы можем определить соответствующую область как распространение,
скажем, от t = 3.3 к t = 7.5. Таким образом мы можем сказать, например,
что контрольная точка Bi центрирована во время t = 5.0 и имеет эффект
в диапазоне от t = 3.3 к t = 7.5.
Рисунок 6 показывает типичный пример того, что базовая функция
могла бы выглядеть, как будто она имеет максимальный эффект в некоторой
определенной точке во времени и сужается от гладко, как будто становится
дальше от точки. Если Вы не спали на курсах по статистике колледжа,
Вы могли бы признавать ее как "звонкообразную кривую",
которую все мы учились знать, но и ненавидеть. Кривая Ni, k (t)
на рисунке показывает, что управляющая точка Bi имеет его самое
большое значение (приблизительно 95 %) во время t = 3.0 и тонкие
свечи от к приблизительно 50 % в t = 1.7 и t = 4.3.

Рисунок 6. Базисная функция для управляющей точки
Так как у каждой контрольной точки есть собственная базисная функция,
кривая NURB со, скажем, пятью управляющими точками будет иметь пять
таких функций, каждая из которых покрывает некоторую область кривой
(то есть некоторый интервал времени). Во время t = 2.3 на рисунке
7, например, управляющая точка B0 имеет вес приблизительно 0.2,
B1 приблизительно 0.7 и B2 приблизительно 0.05. Так как t идет от
0.0 до 7.0, влияние каждой управляющей точки на форму кривой - первоначально
0, увеличивается постепенно до максимума, и затем постепенно спадает
снова до 0, поскольку мы достигаем конца его диапазона измерений.

Рисунок 7. Равномерные базисные функции для набора управляющих
точек
УЗЛЫ
Обратите внимание, что все базисные функции на рисунке 7 имеют
абсолютно одинаковую форму и охватывают равные интервалы времени.
Вообще, мы хотели иметь возможность изменять ширину интервалов (так,
чтобы некоторые управляющие точки затронули большую часть кривой,
а другие меньшую) и максимальную высоту кривых (так, чтобы некоторые
управляющие точки затронули форму кривой сильнее чем другие). От
сюда и происходит аббревиатура NU в NURB: она
обозначает неравномерный (nonuniform).
Решение состоит в том, чтобы определить ряд точек, разделяющие
время на интервалы, которые мы можем затем использовать в базисных
функциях, чтобы достигнуть желаемых эффектов. Изменяя относительные
длины интервалов, мы можем изменить время, в течение которого каждая
контрольная точка влияет на частицу. Точки, разграничивающие интервалы
называются узлами, а упорядоченный их список - вектор узлов (рисунок
8). Вектор узла для функций основания, показанных на рисунке 7 -
{0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0}. Это пример равномерного
(uniform) вектора узлов, благодаря которым все функции на рисунке
охватывают равные интервалы времени. На рисунок 9 изображен пример
кривой, созданной с таким вектором узлов.

Рисунок 8. Вектор узлов
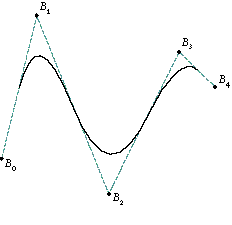
Рисунок 9. NURB-кривая с равномерным вектором узлов
Если мы заменим вектор узлов на {0.0, 1.0, 2.0, 3.75, 4.0, 4.25,
6.0, 7.0}, мы получим набор неоднородных базисных функций, тех,
что показаны на рисунке 10, а соответствующая кривая изображена
на рисунке 11 (с использованием того же набора управляющих точек,
что и на рисунке 9). Обратите внимание, что базисная функции N2,3(t)
и N3,3(t), связанная с управляющими точками B2 и B3, соответственно,
являются более высокими и более узкими чем другие. Если Вы сравните
рисунки 9 и 11, Вы увидите, что кривая на рисунке 11 сильнее смещена
к управляющим точкам B2 и B3, чем кривая на рисунке 9. Это потому
что базисные функции для этих управляющих точек имеют большее максимальное
значение. Кроме того, кривая быстро приближается к этим управляющим
точкам и быстро отдаляется: сравните, как сильно она изогнута около
этих точек, по сравнению с кривой на рисунке 9. Это результат более
узких базисных функций для этих двух управляющих точек: интуитивно,
наша движущаяся частица должна пересечь большую часть пространства
за относительно малое время. Смотря на вектор узла, Вы можете видеть,
что интервалы между узлами для этих двух контрольных точек уже,
чем для других - {3.75, 4.0} и {4.0, 4.25} - это означает, что их
влияния на кривую сконцентрированы в более узких интервалах времени.

Рисунок 10. Неравномерные базисные функции
для управляющих точек

Рисунок 11. NURB-кривая с неравномерным вектором узлов
ОПРЕДЕЛЕНИЕ БАЗИСНЫХ ФУНКЦИЙ
Мы теперь готовы завершить наше определение кривой NURB, точно
определив базисные функции. В некоторых отношениях, мы свободны
выбирать любой вид функций, которые мы хотим, но, выбирая их тщательно,
мы можем получить определенные желаемые эффекты. Определения, которые
мы будем использовать следующие:

где xi - обычный индекс для i-го узла в векторе узлов.
Это определение содержит в себе многое, и большое количество индексов
- мы здесь вникаем в действительные теоретические аспекты кривых
NURB. Обратите внимание, что функции для больших значений индексов
k (называемых заказом(порядком) функции основания) построены рекурсивно
от функций меньшего порядка. Если k - самый высокий порядок функции
основания, которая дает кривую NURB, то говорят, что она имеет порядок
k или что она (k-1)-ой степени. В самом основании иерархии, функции
порядка 1 - это просто 1, если t находится между i-ой и (i+1)-ой
узлами, и 0 в противном случае.
Особенности такого рода наборов базисных функций, и то, как они
стали таковыми, выходит за рамки данной статьи; если Вы хотите узнать
о них больше, Вы найдете все детали, которые Вам возможно нужны
(и даже больше) во "Введении в Сплайны для Использования
в Компьютерном Графическом и Геометрическом Моделировании".
Однако, мы можем по крайней мере упомянуть несколько важных характеристик,
которые проявляет этот набор базисных функций:
- В любое время t, значения всех базисных функций составляют
в целом ровно 1.
- Если все управляющие точки имеют положительные веса, кривая
содержится в пределах ограничивающей области, известной как выпуклая
оболочка. (См. книгу, цитируемую выше для подробностей.)
- В любое время t, не больше, чем k базисных функций влияют на
кривую, где k - это порядок кривой.
- Кривая порядка k определена только там, где k базисные функции
отличны от нуля.
Эта последняя характеристика имеет больше, чем просто теоретический
интерес: кубическая (3-ей степени или 4-го порядок) NURB кривая
с вектором узла, скажем, {0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0}
идет только от t = 3.0 до t = 4.0! Правило состоит в том, что кривая
начинается в k-ом узле от начала вектора узлов и заканчивается в
k-ом узле с конца.
УЗЛЫ И ПЕТЛИ
Я должен указать здесь, что неоднородные векторы узлов не являются
действительно очень полезными для управления формой кривой. (Фактически,
непосредственное перемещение управляющей точки также не так уж полезно
- но мы вернемся к этому позже.) Вместо этого, неоднородные векторы
узлов имеют два важных применения:
- Вы вероятно заметили, что все наши кривые NURB до сих пор имели
оконечные точки только просто "плавая в пространстве";
то есть оконечные точки кривой не совпадают ни с какой управляющей
точкой. В реальной жизни, тем не менее, мы бы хотели иметь возможность
управлять точным размещением оконечных точек, и наиболее часто
мы хотим, чтобы первая и последняя управляющая точка совпали.
- Вы, возможно, также заметили, что до сих пор кривые, отображались
пока весьма гладки. Хотя это обычно хорошая вещь, мы иногда должны
создать кривую с петлей или углом.
Мы можем достичь обе эти цели, используя довольно критический случай
неоднородности: предоставляя нескольких последовательных узлов с
одним и тем же значением t! Например, вектор узлов подобно {0.0,
0.0, 0.0, 3.0, 4.0, 5.0, 6.0, 7.0} производит набор базисных функций,
изображенных рисунке 12 и кривой (используя те же управляющие точки,
что и прежде) на рисунке 13. Смотря рисунок 12, Вы можете видеть,
что в t = 0, базисные функции, связанны со всеми управляющими точками
кроме первой имеет значение 0 - так что базисная функция N0,3(t)
(для управляющей точки B0) имеет полный контроль над кривой. Таким
образом кривая в t = 0 совпадает с первой управляющей точкой.

Рисунок 12. Базисные функции для кривых
с множеством одинаковых узлов в начале

Рисунок 13. NURB кривая с множеством одинаковых узлов в начале.
Если мы скомкаем несколько узлов в середине вектора узлов {0.0,
1.0, 2.0, 3.0, 3.0, 5.0, 6.0, 7.0}, мы получим базисные функции
показанные на рисунке 14 и кривую на рисунке 15. В t = 3.0, все
базисные функции кроме N2,3 (t) имеют значение 0 - так что B2 -
единственная управляющая точка, влияющая на кривую в тот момент,
и таким образом кривая совпадает с данной управляющей точкой.

Рисунок 14. Базисные функции для кривой
с несколькими одинаковыми узлами в середине

Рисунок 15. NURB-кривая с несколькими одинаковыми узлами в середине
В математических терминах, непрерывность (гладкость) - это следствие
только для в соединениях, определенных узлами кривой, где соединяются
два сегмента кривой; между соединениями кривая совершенно гладкая
и непрерывная. Типичная кривая, в которой каждое соединение соответствует
единственному узлу, имеет непрерывность Cn-1, где n - степень кривой.
Так кубическая (3-ей степени или 4-го порядок) кривая имеет непрерывность
по второй производной (C2) в каждом соединении, если все узлы отличны.
Если два узла совпадают, непрерывность в том соединении понижается
на одну степень; если три совпадают, степень непрерывности понижается
на два; и так далее.
Это означает, что Вы можете помещать петлю в кривую в определенной
точке, добавляя узлы к вектору узла в том пункте(точке). Позже,
мы будем смотреть на код, который показывает, как это делается.
Мы также увидим, как можно использовать эту же методику вставки
узла, чтобы преобразовать кривую NURB до Bezier представления.
РАЦИОНАЛЬНЫЕ КРИВЫЕ
Теперь, когда мы узнали все об управляющих точках, узлах и базисных
функциях, мы понимаем NUB (неоднородный B-сплайн) кривые. Но что
на счет остальной части акронима? У нас все еще нет R в NURB. Пришло
время поговорить о рациональных кривых.
Если Вы заглядывали в определения NURB программы QuickDraw 3D,
Вы, возможно, задались вопросом, почему это использует четырехмерное
представление для трехмерных управляющих точек: {x, y, z, w} вместо
только {x, y, z}. Причина для дополнительной координаты - это то,
что это позволяет нам точно представлять конические кривые (круги,
эллипсы, параболы, и гиперболы), также как предоставление нам большего
контроля над формой других кривых. Четвертая координата, w, обычно
упоминается как вес управляющей точки. Обычно, каждая управляющая
точка несет вес 1.0, означая, что они все имеют равное влияние на
форму кривой. При увеличении веса отдельной управляющей точки дает
ей больше влияния и имеет эффект "перемещения" кривой
к этой точке (см. рисунок 16).

Рисунок 16. Увеличение веса управляющей точки
Кривые, которые определенные таким образом, с весом w для каждой
управляющей точки, называются рациональными кривыми. Математически,
такие кривые определены в четырехмерном пространстве (так как управляющие
точки имеют четыре компонента) и проецируются в трехмерном пространстве.
Визуализирующие объекты в четырех измерениях немного сложны (уже
не говоря о рисунке их в диаграмме), но мы можем понимать основную
идею, рассматривая рациональные двумерные кривые: это кривые, определенные
в трехмерном пространстве и проецируемый на плоскость, как показано
на рисунке 17.

Рисунок 17. Проецирование трехмерной кривой в второе измерение
Это - по существу тот же самый процесс, что и проецирование трехмерной
модели на двумерный экран с перспективной камерой. Основной метод
для такого перспективного проектирования состоит в том, чтобы делить
на гомогенный компонент вершины (то есть на w); мы используем аналогичный
подход проектировать нашу четырехмерную рациональную кривую в трехмерное
пространство(пробел). Математически, мы должны включить это деление
в наше раннее определение для кривой B-сплайна:

Bi - это проекции четырехмерных контрольных точек, а wi - их веса.
Есть два различных преобразования представления управляющих точек
в терминах их четырехмерных координат {x, y, z, w}:
- Гомогенное (однородное), в котором координаты представляют
позицию точки в четырехмерном пространстве. Чтобы проецировать
их в третье измерение, компоненты должны весь быть разделенными
через w. Таким образом трехмерная позиция пункта(точки) - фактически
{x/w, y/w, z/w}. (Обратите внимание, что w/w - всегда 1.)
- Взвешенное Эвклидово, в котором предполагается, что
координаты уже разделены. Таким образом первые три компонента
{x, y, z} непосредственно представляют позицию точки в трехмерном
пространстве, и четвертый (w) представляет его вес.
QuickDraw 3D использует гомогенное представление, как делается
в большинстве технических документах и других графических библиотеках.
Я сказал ранее, что мы могли использовать рациональный коэффициент
кривых NURB, чтобы создать конические отрезки (типа кругов и эллипсов).
Конические отрезки так названы, потому что они являются кривыми,
которые мы получает путем пересечения конуса с плоскостью; угол,
под которым самолет пересекает конус, определяет, является ли итоговая
кривая кругом, эллипсом, параболой, или гиперболой. Строго говоря,
гиперболы и параболы имеют бесконечную степень - но бесконечные
кривые вообще бесполезны в прикладных программах работы с графикой
(кроме того для них очень сложно вычислить охватывающую его коробку).
Так что мы ограничим наше обсуждение коническими дугами.
Так как конические кривые квадратичные, мы можем представлять их
квадратичной (степени 2 или порядка 3) NURB кривой. Практический
вопрос, конечно, для NURB кривой. Хотя доказательство выходит за
рамки данной статьи, следующий метод (изображенный на рисунке 18)
может использоваться, чтобы генерировать конические дуги:
Рисунок 18. Построение конических дуг
- Кривая определена тремя управляющими точками. Первая и последняя
являются оконечными точками конической дуги, в то время как размещение
внутренней управляющей точки определяет форму кривой.
- Веса первой и последней управляющих точек равно 1.0.
- Вес меньше, чем 1.0 для внутренней управляющей точки генерирует
эллипс; вес, равный 1.0 генерирует параболу; вес большее чем 1.0
генерирует гиперболу.
- Вектор узлов равен {0.0, 0.0, 0.0, 1.0, 1.0, 1.0}.
Вероятно наиболее общая форма конической дуги, особенно в приложениях
моделировании и проектирования, является круговой дугой. Так как
круг - просто специальный случай эллипса, метод построения дуги
окружности - специальный случай общего метода для эллиптических
дуг:
- стороны управляющего многоугольника имеют равную длину (то
есть управляющий треугольник является равнобедренным).
- Хорда, соединяющая первую и последнюю управляющие точки сводят
каждую сторону под углом [[theta]], равным половине угла желаемой
дуги (например, 30 градусов для 60-градусной дуги).
- Вес внутренней управляющей точки равен косинусу [[theta]].
- Вектор узлов - {0.0, 0.0, 0.0, 1.0, 1.0, 1.0}, также, как в
предыдущем случае.
Рисунок 19 иллюстрирует эту идею. (В этом случае, управляющий треугольник
равносторонний, так что угол [[theta]] равен 60 градусам, а результирующая
дуга равна 120 градусам, или одной трети круга.)

Рисунок 19. Построение дуги окружности
Обратите внимание, что предшествующий метод может создавать только
дугу меньше 180 градусов; для больших дуг, мы должны собрать вместе
части несколько NURB кривых. Таким образом, чтобы нарисовать полный
круг мы могли объединяться три 120-градусные дуги или четыре 90-градусные.
Однако, возможно представить эти три или четыре отдельных дуги как
одну кривую и делать круг только из одной кривой NURB. Рисунки 20
и 21 показывают, как это делается с тремя и четырьмя дугами, соответственно.

Рисунок 20. Построение окружности из трех
дуг

Рисунок 21. Построение окружности из четырех дуг
NURB КРИВЫЕ В QuickDraw 3D
К настоящему времени Вы вероятно говорите, " Достаточно теории
уже - как это все касается программирования на Macintosh? "
Так давайте наконец посмотрим на структуры данных QuickDraw 3D и
подпрограммы для работы с кривыми NURB.
СТРУКТУРЫ ДАННЫХ
Если Вы следили за обсуждением до сих пор, Вы можете вероятно предполагать
о содержании структуры данных, представляющей кривую NURB: порядок
кривой, ее управляющие точки и узлы. Есть также обычный набор атрибутов
QuickDraw 3D, так что Вы можете рисовать ваши кривые, скажем, в
фуксией или алым цветом. Вот определения:
typedef struct TQ3RationalPoint4D {
float x;
float y;
float z;
float w;
} TQ3RationalPoint4D;
typedef struct TQ3NURBCurveData {
unsigned long order; // Степень кривой
unsigned long numPoints; // Число управляющих точек
TQ3RationalPoint4D *controlPoints; // Массив управляющих точек
float *knots; // Массив узлов
TQ3AttributeSet curveAttributeSet; // атрибуты QuickDraw 3D
} TQ3NURBCurveData;
Большая часть определения довольно ясна, но вот - несколько вещей,
которые следует иметь в виду:
- Порядок кривой должен быть заключен между 2 и 16 включительно.
Порядок 2 дает Вам эффект ломаной линии; наиболее обычным являются
порядки 3 (квадратичные) и 4 (кубические).
- Управляющие точки представлены в гомогенной (однородной) форме,
что означает, что Вы должны делить компоненты x, y, и z на компонент
w, чтобы найти фактическую позицию точки в трехмерном пространстве.
- Компонент W каждой управляющей точки должен быть положителен.
- Число управляющих точек должен быть равен или больший порядка.
- Число узлов должен быть равно числу управляющих точек плюс порядок
кривой.
- Узлы должны быть определены в неубывающем порядке.
- Если k - это порядок кривой, то не могут быть больше (k-1)-го
узла с тем же самым значением (кроме как вначале или конце последовательности,
где допустимо k последовательных равных узлов).
Набор атрибутов должен содержать только атрибуты, которые имеют
смысл для кривой. Наиболее часто, набор атрибутов будет или NULL
или просто содержать цвет.
ВИЗУАЛИЗАЦИЯ КРИВОЙ NURB
Если Вы знакомы с QuickDraw 3D, Вы знаете, что есть два способа
визуализировать графический объект (называемый геометрия в терминологии
QuickDraw 3D): сохраненный режим (retained mode) и непосредственный
режим (immediate mode). В сохраненном режиме, Вы сначала создаете
объект(цель), представляющий фигуру, которую Вы хотите нарисовать,
затем используете этот сохраненный объект, чтобы нарисовать
ваш рисунок. (См., статью "Основы геометрии QuickDraw 3D"
в 23-м выпуске журнала develop, чтобы узнать больше.) Распечатка
1 показывает, как это работает для кривой NURB. Сначала мы инициализируем
структуру TQ3NURBCURVEDATA, описывающую кривую, которая должна быть
нарисована; мы используем эту структуру, чтобы создать сохраненный
объект(цель) с QuickDraw 3D функцией Q3NURBCurve_New, и затем мы
передаем полученный объект к Q3Geometry_Submit, чтобы визуализировать
кривую. Наконец, мы освобождаем сохраненным объектом, который мы
создавали.
Распечатка 1. Визуализация кривой NURB в сохраненном режиме
TQ3GeometryObject curveObject;
TQ3NURBCurveData curveData;
static TQ3RationalPoint4D controlPoints[4] = {
{ 0, 0, 0, 1 },
{ 1, 1, 0, 1 },
{ 2, 0, 0, 1 },
{ 3, 1, 0, 1 }
};
static float knots[8] = {
0, 0, 0, 0, 1, 1, 1, 1
};
// Инициализация структур данных
curveData.order = 4;
curveData.numPoints = 4;
curveData.controlPoints = controlPoints;
curveData.knots = knots;
curveData.curveAttributeSet = NULL;
// Создать сохраненный объект
curveObject = Q3NURBCurve_New(&curveData);
// Использовать сохраненный объект, чтобы визуализировать кривую
Q3View_StartRendering(view);
do {
Q3Geometry_Submit(curveObject, view);
} while (Q3View_EndRendering(view) == kQ3ViewStatusRetraverse);
// Освобождение объект-кривой
Q3Object_Dispose(curveObject);
Эквивалентная операция рисования в непосредственном режиме использует
тот же самый код до точки, где создается объект. Вместо создания
сохраненного объекта, мы просто передаем структуру TQ3NURBCURVEDATA
непосредственно QuickDraw 3D функции Q3NURBCurve_Submit, которая
будет визуализирована сразу:
// Визуализировать кривую непосредственно.
Q3View_StartRendering(view);
do {
Q3NURBCurve_Submit(&curveData, view);
} while (Q3View_EndRendering(view) == kQ3ViewStatusRetraverse);
УПРАВЛЕНИЕ РАЗБИЕНИЕМ
QuickDraw трехмерный не визуализирует кривые NURB непосредственно,
как он это делает, скажем, для линий или треугольников. Чтобы нарисовать
кривую NURB, визуализатор должен разбить ее в последовательность
линий или ломаных. Чем большее количество линий, тем она плавнее
выглядит, но конечно требуется больше времени для ее визуализации.
Перед визуализацией кривой, Вы должны сообщить визуализатору, как
точно Вы хотите разбить.
Для этого есть три возможности, обозначенные значениями перечисляемого
типа данных:
typedef enum TQ3SubdivisionMethod {
kQ3SubdivisionMethodConstant,
kQ3SubdivisionMethodWorldSpace,
kQ3SubdivisionMethodScreenSpace
} TQ3SubdivisionMethod;
- Первый метод, kQ3SubdivisionMethodConstant, говорит разбивать
кривую в ломаную линию с указанном числом отрезков между каждой
парой соединений.
- Второй метод, kQ3SubdivisionMethodWorldSpace, говорит разбивать
кривую так, чтобы длина каждого отрезка строки была не больше
указанного значения, измеренного в мировом координатах.
- Третий метод, kQ3SubdivisionMethodScreenSpace, похож на второй,
но измерение сделано экранных координатах.
Следующая структура данных определяет метод подразделения, который
нужно использовать и соответствующие значения параметров:
typedef struct TQ3SubdivisionStyleData {
TQ3SubdivisionMethod method;
float c1;
float c2;
} TQ3SubdivisionStyleData;
NURB кривые используют только компонент c1; другие - для NURB поверхностей.
Пара вещей, на которые нужно обратить внимание:
- Вы должны установить и c1, и c2 правильные значения. QuickDraw
3D не знает, что поступает, кривая или поверхность, так что он
всегда проверяет оба параметра на правильность. Если Вы только
рисуете кривую, Вы можете также устанавливать c2 в то же самое
значение, что и c1.
- Если Вы определяете, что неправильное значение для другого параметра,
QuickDraw 3D подставит более подходящий и выдаст предупреждение.
Это не позволит Вам разбить кривую в миллион точек!
- Для метода kQ3SubdivisionMethodConstant, c1 должен быть целым
числом большим 0; дробные значения будут усечены.
- Если Вы не определяете стиль разбиения, будет использоваться
значение по умолчанию.
Подробно останавливаясь на нашем примере непосредственного режима
визуализации, следующий код визуализирует нашу кривую NURB ломаной
линией с пятью отрезками между каждой парой узлов:
TQ3SubdivisionStyleData subdivData;
...
subdivData.method = kQ3SubdivisionMethodConstant;
subdivData.c1 = subdivData.c2 = 5;
...
Q3View_StartRendering(view);
do {
Q3SubdivisionStyle_Submit(&subdivData, view);
Q3NURBCurve_Submit(&curveData, view);
} while (Q3View_EndRendering(view) == kQ3ViewStatusRetraverse);
РЕДАКТИРОВАНИЕ NURB КРИВЫХ
Если Вы визуализируете свою кривую в непосредственном режиме, Вы
можете редактировать кривую, просто изменяя ее контрольные точки,
веса, и векторы узла непосредственно в структуре TQ3NURBCURVEDATA.
Если Вы используете сохраненный режим, QuickDraw 3D обеспечит вызовы
для получения и установки отдельных управляющих точек и узлов:
TQ3Status Q3NURBCurve_GetControlPoint(TQ3GeometryObject curve,
unsigned long pointIndex, TQ3RationalPoint4D *point4D);
TQ3Status Q3NURBCurve_SetControlPoint(TQ3GeometryObject curve,
unsigned long pointIndex, const TQ3RationalPoint4D *point4D);
TQ3Status Q3NURBCurve_GetKnot(TQ3GeometryObject curve,
unsigned long knotIndex, float *knotValue);
TQ3Status Q3NURBCurve_SetKnot(TQ3GeometryObject curve,
unsigned long knotIndex, float knotValue);
Поскольку мы не взаимодействуем с элементами, которыми являются
сами объекты, то нет никакого счетчика ссылок и нет никакой нужды
освобождать какие-либо структуры данных. Однако, обратите внимание,
что, если Вы редактируете узел, результирующий вектор узлов недолжен
уменьшаться и следовать ограничениям, описанными ранее для множественных
узлов.
Вы, возможно, заметили, что нет никаких вызовов добавления, удаления,
или переупорядочения управляющих точек или узлов. Вместо этого,
QuickDraw 3D предусматривает вызовы для получения и замены всей
структуры TQ3NURBCURVEDATA сохраненного объекта(цели):
TQ3Status Q3NURBCurve_GetData(TQ3GeometryObject curve,
TQ3NURBCurveData *nurbCurveData);
TQ3Status Q3NURBCurve_SetData(TQ3GeometryObject curve,
const TQ3NURBCurveData *nurbCurveData);
Если Вы хотите изменить число управляющих точек и узлов кривой,
Вы должны делать локальную копию структуры данных, которая Вы получаете
от Q3NURBCurve_GetData (удостоверившись, что Вы распределили дополнительное
место для новых узлов и управляющих точек), изменяете массивы в
локальной копии, и сохраняя их назад в объект с помощью Q3NURBCurve_SetData.
Вы должны затем вызвать следующую подпрограмму, чтобы распорядиться
данными, которые Вы получили от Q3NURBCurve_GetData:
TQ3Status Q3NURBCurve_EmptyData(TQ3NURBCurveData *nurbCurveData);
Однако, если Вы собираетесь часто изменять кривую NURB, Вы должны
вероятно работать в непосредственном режиме и не использовать сохраненного
объекта вообще.
ВСТАВКА УЗЛА
Вообще, чем большее количество контрольных точек, которые мы определяем
для кривой NURB, тем большее контроля, мы имеет над о его форме.
Казалось бы разумно, если бы мы могли добавлять большее количество
контрольных точек без того, чтобы изменить форму кривой, и фактически
так оно и есть. Помните, тем не менее, что есть фундаментальные
отношение между узлами, управляющими точками, и порядком кривой:
число узлов равен числу контрольных точек плюс порядок. Например,
кубическая кривая (порядока 4) с 9 управляющими точками будет требовать
13 узлов. Так каждый раз, добавляя управляющую точку, мы также должны
добавить дополнительный узел - и удостовериться, что все управляющие
точки имеют правильное местоположение, чтобы сохранить форму кривой
такой, какой она была.
На практике, мы вообще-то берем обратный подход: мы решаем, где
добавить новый узел, затем вычисляем местоположение соответствующей
новой управляющей точки (также как новые местоположения некоторых
из существующих). Например, если мы берем кривую, изображенную ранее
на рисунке 9 и вставляем новый узел в t = 3.6, мы получаем новую
кривую с точно той же самой формой, но с новым набором контрольных
точек (рисунок 22).

Рисунок 22. Вставка узла
Эта операция вставки узла является фундаментальной в работе с кривыми
NURB. Это непосредственно полезно как для изменения (редактирования),
так и для визуализации кривых, и может также использоваться для
преобразования кривой NURB к Bеzier представлению. После краткого
обзора математического алгоритма для вставки узла, мы взглянем на
некоторый пример его реализации с коде языка C.
АЛГОРИТМ
Мы начнем с кривой NURB, представленной как
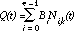
с вектором узла {x0, x1..., xn+k-1}. Предположим, что мы хотим
добавить новый узел xnew, где xi < xnew < = xi+1. Новый вектор
узла ^x - просто старый вектор узла с xnew, вставленным между xi
и xi+1. Новая кривая будет определена как

с вектором узла ^x.
Теперь мы должны выяснить не только, где расположена новая управляющая
точка и где она находится в упорядоченном векторе управляющих точек,
но также и как откорректировать некоторых из существующих управляющих
точек, чтобы сохранить форму кривой неизменной; этот процесс выдает
новый вектор управляющих точек, ^B. Оказывается, что соотношение
между старыми и новыми управляющими точками следующее:

где [[альфа]] определена как

Доказательство этого относительно простое, но мы не имеем времени
или места, чтобы вникнуть в него здесь. Для полного рассмотрения,
см. Curves and Surfaces in Computer Aided Geometric Design (Кривые
и поверхности в компьютерном геометрическом проектировании).
РЕАЛИЗАЦИЯ
Распечатка 2 показывает функцию реализации этого основного алгоритма.
Функция, которая включена в компакт-диск этого выпуска, принимает
структуру данных NURB-кривой библиотеки QuickDraw 3D в качестве
параметра, наряду со значением нового узла, который нужно вставить,
и возвращает новую структуру данных, представляющую ту же самую
кривую с новым вставленным узлом. Для краткости, функция не выполняет
никакой проверки диапазона на вставленный узел, а просто предполагает,
что он лежит в пределах допустимого диапазона и что результирующий
вектор узлов подчиняется обычным ограничениям на множественные узлы.
Обратите внимание также, что код, показанный здесь не делает никакой
проверки на результаты запросов распределения памяти, хотя, конечно,
Вы должны всегда исполнять такие проверки в реальной жизни.
Распечатка 2. Вставка узла
static TQ3NURBCurveData *InsertKnot
(TQ3NURBCurveData *oldCurveData, // Старая кривая
float tNew) // Вставляемый узел
{
TQ3NURBCurveData *newCurveData; // Новая кривая после добавления узла
unsigned long k; // Порядок кривой
unsigned long n; // Число управляющих точек
TQ3RationalPoint4D *b; // Вектор старых управляющих точек
TQ3RationalPoint4D *bHat; // Вектор новых управляющих точек
float *x; // Старый вектор узлов
float *xHat; // Новый вектор узлов
float alpha; // коэффициент интерполяции
unsigned long i; // Узел, после которого нужно вставлять
unsigned long j; // Номер узла для поиска
TQ3Boolean foundIndex; // Найден ли индекс вставки?
// Установить локальные переменные для надежности.
k = oldCurveData->order;
n = oldCurveData->numPoints;
x = oldCurveData->knots;
b = oldCurveData->controlPoints;
// Выделить место для новых управляющих точек и вектора узлов.
bHat = malloc((n + 1) * sizeof(TQ3RationalPoint4D));
xHat = malloc((n + k + 1) * sizeof(float));
// Выделить структуру данных для новой кривой.
newCurveData = malloc(sizeof(TQ3NURBCurveData));
newCurveData->order = k;
newCurveData->numPoints = n + 1;
newCurveData->controlPoints = bHat;
newCurveData->knots = xHat;
newCurveData->curveAttributeSet =
(oldCurveData->curveAttributeSet == NULL)
? NULL
: Q3Object_Duplicate(oldCurveData->curveAttributeSet);
// Найти место для вставки нового узла.
for (j = 0, foundIndex = kQ3False; j < n + k; j++) {
if (tNew > x[j] && tNew <= x[j + 1]) {
i = j;
foundIndex = kQ3True;
break;
}
}
// Выйти, если не найдено.
if (!foundIndex) {
return (NULL);
}
// Копировать узлы в новый вектор.
for (j = 0; j < n + k + 1; j++) {
if (j <= i) {
xHat[j] = x[j];
} else if (j == i + 1) {
xHat[j] = tNew;
} else {
xHat[j] = x[j - 1];
}
}
// Вычислить позицию новой управляющей точки и новую позицию
// существующей.
for (j = 0; j < n + 1; j++) {
if (j <= i - k + 1) {
alpha = 1;
} else if (i - k + 2 <= j && j <= i) {
if (x[j + k - 1] - x[j] == 0) {
alpha = 0;
} else {
alpha = (tNew - x[j]) / (x[j + k - 1] - x[j]);
}
} else {
alpha = 0;
}
if (alpha == 0) {
bHat[j] = b[j - 1];
} else if (alpha == 1) {
bHat[j] = b[j];
} else {
bHat[j].x = (1 - alpha) * b[j - 1].x + alpha * b[j].x;
bHat[j].y = (1 - alpha) * b[j - 1].y + alpha * b[j].y;
bHat[j].z = (1 - alpha) * b[j - 1].z + alpha * b[j].z;
bHat[j].w = (1 - alpha) * b[j - 1].w + alpha * b[j].w;
}
}
return (newCurveData);
}
ВЫЧИСЛЕНИЕ NURB КРИВЫХ
Вспомните из нашего раннего обсуждения, о том что, если мы имеем
два узла в том же самом местоположении, мы теряем одну степень непрерывности;
с тремя идентичными узлами, мы теряем две степени непрерывности;
и так далее. Этот процесс не можно повторять до тех пор, когда мы
достигаем k-1 идентичных узлов (где k - порядок кривой), пока у
нас не будет непрерывности вообще в данной точке. В этом случае,
кривая в этой точке совпадает непосредственно с управляющей точкой,
как мы видели на рисунке 15.
Мы только что видели, что мы можем добавлять узел xnew и вычислить
новые управляющие точки. Если мы возьмем эту "новую" кривую
(в действительности старый, только с большим количеством узлов)
и добавим тот же самый узел снова и снова, пока у нас не будет k-1
узлов в одном месте, мы получим управляющую точку, которая находится
точно в ^ Q (xnew). Мы можем использовать эту методику, чтобы вычислить
местоположение определенной точки на кривой NURB: просто продолжите
вставлять узлы в интересующую вас точку до тех пор, когда их будет
k-1, тогда новая созданная управляющая точка будет лежать в нужной
точке кривой.
Мы можем также использовать этот подход для визуализации кривой:
добавляя достаточное количество узлов в некоторое число последовательных
во времени t точек. После этого у нас будет список вычисленных на
кривой точек, которую мы можем тогда визуализировать как ломаную
линию. Чем больший число вычисленных точек, тем большее количество
сегментов будет у ломаной линии, и, точнее результирующее изображение
приблизит кривую.
Это - не самый эффективный алгоритм; существует множество лучших
альтернатив. Например, см. An Introduction to Splines for Use
in Computer Graphics and Geometric Modeling для описания алгоритма
Осло, который является заметно более эффективным, если Вы добавляете
больше, чем несколько knots.*
NURB КРИВЫЕ И КРИВЫЕ BEZIER
Если Вы знакомы с кривыми Bezier, Вы можете задастся вопросом,
как они касаются кривых NURB. В частности если ваше приложение в
настоящее время использует кривые Bezier, как Вы можете их рисовать,
когда QuickDraw 3D в настоящее время поддерживает только кривые
NURB? Хотя полная обработка данной темы выходит за пределы данной
статьи, Вы будете счастливы узнать, что кривые Bezier могут фактически
рассматриваться как подмножество кривых NURB. В результате, преобразование
из Bezier в NURB представление, оказывается, тривиальным.
ПРЕОБРАЗОВАНИЕ КРИВЫХ BEZIER В КРИВЫЕ NURB
Вот все, что требуется для преобразования кривой Bezier к формату
NURB:
- Используйте управляющие точки Bezier как управляющие точки
NURB. Если контрольные точки Bezier рациональны (то есть если
они имеют четыре компонента {x, y, z, w}), удостоверьтесь, что
они находятся в гомогенной, а не взвешенной Эвклидовой форме.
Если они нерациональны (не имеют никакого w компонента), просто
устанавливаете w = 1.0 для каждой NURB контрольной точки.
- Установите порядок кривой NURB к числу управляющих точек. Bezier
кривые типично имеют три или четыре контрольных точки, соответствуя
квадратичным (порядок 3) или кубическим (порядок 4) NURB кривым,
соответственно.
Создайте вектор узла с 2k элементами, где k - порядок кривой. Установите
первые k узлов в 0.0, а последние k к 1.0.
Распечатка 3 показывает функцию восполнения преобразование (оно
включено в компакт-диск этого выпуска). Предположим, что кривая
Bezier представлена структурой данных формы
typedef struct BezierCurve {
unsigned int order;
Point3D *controlPoints;
} BezierCurve;
Распечатки 3. Преобразование кривой Bezier в NURB представление
TQ3NURBCurveData *BezierToNURBCurve(BezierCurve *bezCurve)
{
TQ3NURBCurveData *nurbCurveData; // Структура данных кривой NURB
unsigned long k; // Порядок кривой
Point3D *b; // Вектор управляющий точек Bezier
unsigned long i; // Управляющая точка или индекс узла
// Установить локальные переменные для надежности.
k = bezCurve->order;
b = bezCurve->controlPoints;
// Выделить структуру данных для новой кривой.
nurbCurveData = malloc(sizeof(TQ3NURBCurveData));
nurbCurveData->order = k;
nurbCurveData->numPoints = k;
nurbCurveData->controlPoints = malloc(k*sizeof(TQ3RationalPoint4D));
nurbCurveData->knots = malloc(2*k*sizeof(float);
// Создать управляющие тоски.
for (i = 0; i < k; i++) {
TQ3RationalPoint4D_Set(&nurbCurveData->controlPoints[i],
b[i].x, b[i].y, b[i].z, 1.0);
}
// Создать новый узел.
for (i = 0; i < k; i++) {
nurbCurveData->knots[i] = 0.0;
nurbCurveData->knots[i + k] = 1.0;
}
// Установить здесь атрибуты, если требуется.
nurbCurveData->nurbCurveAttributes = NULL;
return (nurbCurveData);
}
где число управляющих точек равно порядку кривой. Функция возвращает
структуру TQ3NURBCURVEDATA, представляющую эквивалент NURB кривой.
Еще раз, мы сэкономили место, занимаемое кодом, опустив необходимые
проверки результатов запросов распределения памяти.
ПРЕОБРАЗОВАНИЕ NURB В КРИВЫЕ BEZIER
Преобразование кривой NURB к формату Bezier более сложное, чем
обратное. Поскольку мы только что видели, любая кривая Bezier может
быть представлена определенным типом кривой NURB, имея половину
ее узлов в одном конце и половину в другом. Обратное, однако, не
верно: произвольная кривая NURB не может, вообще говоря, быть представлена
единственной кривой Bezier. Фактически, вообще-то требует несколько
Bezier кривых для представления единственной кривой NURB: по одной
для каждого сегмента кривой, как определено ее вектором узлов.
Вспомните, что на каждый сегмент кривой NURB влияет некоторое подмножество
управляющих точек. Если мы возьмем каждый сегмент и добавим узлы
к обоим концам, каждый раз генерируя новый набор управляющих точек,
пока у каждого конца число узлов не будет равняются порядку кривой,
результатом будет Bezier представление определенного сегмента. Если
делать это для каждого сегмента, то мы получим с ряд кривых Bezier,
который будет похож на оригинальную NURB кривую.
ПРОЕКТИРОВАНИЕ С ПОМОЩЬЮ КРИВЫХ NURB
Тема о том, как использовать кривые NURB в проектировании могла
бы легко заполнять целую книгу; мы должны будем довольствоваться
лишь кратким обсуждением, наряду с некоторыми указаниями для дальнейшего
чтения.
Наиболее очевидные возможности, которые может предлагать прикладная
программа для создания и изменения NURB кривым, следующие
- интерактивное размещение и движение управляющих точек
- интерактивное размещение и движение узлов
- интерактивное установка и модификация весов контрольной точки
Эти возможности могут быть умеренно эффективными, но фактически
их использование для моделирования желательной формы оказывается
трудным и неуклюжим. Кроме того, изменяя управляющую точку, узел
или вес будут вообще-то затрагивать части кривой, которую пользователь
хотел бы оставить неизменной.
Одна из проблем, которая была широко исследована - это автоматическое
создание кривой, которая интерполирует данный набор точек, которые,
возможно, были в интерактивном режиме размещены пользователем или
получены некоторым видом выборки данных. Действительно, можно сказать,
что это было одно из первоначальных побуждений для математического
развития сплайновых кривых. Первые прямые попытки давали менее,
чем удовлетворительные результаты, но более поздние усилия были
не так плохи и даже полезны, если кривая проходит точно через данные
точки. Однако часто мы только должны приблизить данный набор точек
сплайновой кривой. Точки, возможно, были получены путем выборки
данных ручного рисунка пользователя с помощью мыши или планшета,
измерением физического объекта или извлечением информации из глифа
в растровом шрифте. В этих случаях, мы вероятно хотим сохранить
такие особенности, как оконечные точки и углы, но остающиеся выборки
данных могут быть зашумленные или несглаженные и нуждаться в неточном
подборе. Методы и для точного, и для приблизительного подборов могут
быть найдены в Phoenix: An Interactive Curve Design System Based
on the Automatic Fitting of Hand-Sketched Curves and A User Interface
Model and Tools for Geometric Design. Эти методы могут также
быть приспособлены к использованию при изменении существующей кривой,
была ли она сгенерирована обычным способом или одним из алгоритмов
подбора.
ЗАКРУГЛЯЕМСЯ
Хорошо, вот, что Вы имеете: больше чем Вы вероятно хотели знать
о кривых NURB, плюс некоторый свободный код для загрузки. Ищите
возможную выходящую статью о NURB поверхностях, и как кривые NURB
и поверхности могут использоваться вместе для проектирования объектов
и управления движением.
БИБЛИОГРАФИЯ И РЕКОМЕНДУЕМОЕ ЧТЕНИЕ
Эта статья только затрагивает вершину айсберга теории, лежащей
в основе NURB кривых. Далее располагается список книг и статей,
упомянутых в данной статье, также как другие Вы можете захотеть
исследовать для дополнительной информации.
- Curves and Surfaces for Computer Aided Geometric Design:
A Practical Guide by Gerald Farin (Academic Press, 1990).
- Curves and Surfaces in Computer Aided Geometric Design by
Fujio Yamaguchi (Springer-Verlag, 1988).
- Fundamentals of Computer Aided Geometric Design by Josef
Hoschek and Dieter Lasser (A. K. Peters, 1993).
- An Introduction to Splines for Use in Computer Graphics
and Geometric Modeling by Richard H. Bartels, John C. Beatty,
and Brian A. Barsky (Morgan Kaufman Publishers, 1987).
- Mathematical Elements for Computer Graphics by David F.
Rogers and J. Alan Adams (McGraw-Hill, 1976).
- NURB Curves and Surfaces from Projective Geometry to Practical
Use by Gerald Farin (A. K. Peters, 1995).
- Phoenix: An Interactive Curve Design System Based on the
Automatic Fitting of Hand-Sketched Curves by Philip J. Schneider
(master's thesis, University of Washington, 1988).
- "A Survey of Curve and Surface Methods in CAGD"
by Wolfgang Bohm, Gerald Farin, and Jurgen Kahman, in Computer
Aided Geometric Design, volume 1 (1984)
- A User Interface Model and Tools for Geometric Design by
Michael J. Banks (master's thesis, University of Utah, 1989).

Филип Дж. Шнейдер (pjs@apple.com)
- наиболее долгоживущий член команды QuickDraw 3D. Он живет с его
женой Сюзанной и сыном Дакота по среди леса красного дерева в горах
Санта-Круза, претворяясь, что он так делает, потому что " это
более возможно. " Люди, обманутые этой выдумкой, вероятно также
полагают, что он не любит ездить на работу каждый день по двусторонней
пригородной магистрали, и предпочел бы быть застрять в пробке на
межгосударственной автостраде. Его текущие проекты включают попытку
единолично поднять всемирный уровень компьютерной технологии к тому,
что он находит в романах научной фантастики, которую он жадно читает,
и обучение его 18-месячного сына менять его собственные пеленки
посреди ночи *
Спасибо нашим техническим рецензентам Пабло Ферниколе, Джиму Милдрю,
Клаусу Стрело, и Нику Томпсону.*
Из
выпуска №25
Перевод с английского: Кудря Вячеслав
mailto:putyavka@urktop.com
[На главную страницу]
|