Навигация
Савков Дмитрий Александрович
Тема магистерской работы: "Разработка системы моделирования профилей гидрофизических параметров"
Руководитель: доцент Светличная Виктория Антоновна
Диссертация
- Введение
- Постановка задачи
- Анализ существующих методов
- Результаты работы
- Заключение
- Список используемой литературы
Методы моделирования полей турбулентности
Для построения детальной модели случайных полей с мелкомасштабной перемежаемостью, будем понимать под
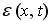 поле любой локальной неотрицательной гидродинамической характеристики, определяемой только мелкомасштабными компонентами турбулентности (это может быть не только скорость диссипации турбулентной энергии, но и, например, квадрат или абсолютная величина какой-либо пространственной производной от поля скорости или температуры или другого скалярного поля, или же скорость вырождения неоднородностей температурного поля, или квадрат вихря скорости, или квадрат разности скоростей или температур в двух близких точках пространства, или произведение степеней двух или нескольких таких величин и т.п.
поле любой локальной неотрицательной гидродинамической характеристики, определяемой только мелкомасштабными компонентами турбулентности (это может быть не только скорость диссипации турбулентной энергии, но и, например, квадрат или абсолютная величина какой-либо пространственной производной от поля скорости или температуры или другого скалярного поля, или же скорость вырождения неоднородностей температурного поля, или квадрат вихря скорости, или квадрат разности скоростей или температур в двух близких точках пространства, или произведение степеней двух или нескольких таких величин и т.п.
Рассмотрим последовательность вложенных друг в друга и подобных друг другу областей пространства, с одним и тем же отношением масштабов последовательных областей. Пусть
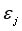 среднее значение поля
среднее значение поля
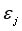 по области
по области
 .
Введем случайные величины
.
Введем случайные величины
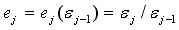 рассматриваемые при фиксированных значениях знаменателей. Тогда
рассматриваемые при фиксированных значениях знаменателей. Тогда
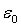 может быть отождествлено с математическим ожиданием
может быть отождествлено с математическим ожиданием
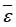 поля
поля
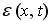 и все величины
и все величины
 с такими индексами j, что
с такими индексами j, что
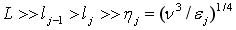 являются независимыми одинаково распределенными случайными величинами (здесь
являются независимыми одинаково распределенными случайными величинами (здесь
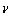 – кинематический коэффициент молекулярной вязкости). При этом
– кинематический коэффициент молекулярной вязкости). При этом
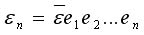 , так что
, так что

В случае полностью развитой турбулентности (при очень большом числе Рейнольдса Re) интервал масштабного подобия будет достаточно широким, и в сумме в правой части равенства (2.1) будет содержаться много независимых одинаково распределенных слагаемых
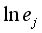 так что в силу центральной предельной теоремы теории вероятностей эта сумма будет иметь приблизительно нормальное распределение с математическим ожиданием и дисперсией следующего вида:
так что в силу центральной предельной теоремы теории вероятностей эта сумма будет иметь приблизительно нормальное распределение с математическим ожиданием и дисперсией следующего вида:
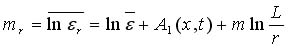
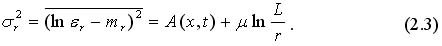
Изложенная модель с дискретным дроблением пространственных областей, приводящая к логарифмически-нормальному распределению для
 была рассчитана Гурвичем А. С. и Ягломом А. М. Затем Новиков Е. А. [4] развил более общий подход, не требующий дискретности дробления и связанный с рассмотрением коэффицентов дробления.
была рассчитана Гурвичем А. С. и Ягломом А. М. Затем Новиков Е. А. [4] развил более общий подход, не требующий дискретности дробления и связанный с рассмотрением коэффицентов дробления.
Крейчнан Р. Г. высказал мнение, что лежащее в основе теории Колмогорова – Обухова 1962 г. представление о каскадном процессе дробления турбулентных вихрей, обладающем масштабным подобием и порождающем перемежаемость турбулентности, систематически возрастающую при уменьшении масштабов, не требует логарифмической нормальности средних значений скорости диссипации энергии по малым областям пространства, а допускает другие возможности. В этой связи особый интерес приобретают соответствующие экспериментальные данные. Расчеты статистических характеристик коэффициентов дробления
 по данным измерений турбулентных пульсации скорости ветра в приземном слое атмосферы подтвердили выполнение условий масштабного подобия в масштабах, больших по сравнению с микромасштабом Колмогорова
по данным измерений турбулентных пульсации скорости ветра в приземном слое атмосферы подтвердили выполнение условий масштабного подобия в масштабах, больших по сравнению с микромасштабом Колмогорова
 .
.
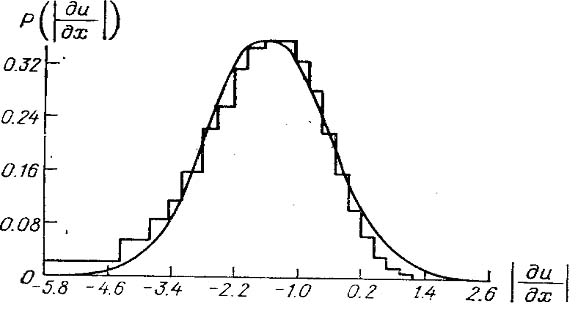
Построения эмпирических функций распределения вероятности для неотрицательных мелкомасштабных гидродинамических характеристик типа
 показали, что эти функции неплохо аппроксимируются логарифмически-нормальным распределением с заметными отклонениями от него в области малых значений рассматриваемой случайной величины, эмпирические вероятности которых оказываются больше, чем по логарифмически-нормальному распределению, так как к этим малым значениям при измерениях прибавляется инструментальный шум. В качестве примера на рис. 6 приводится гистограмма значений случайной величины
показали, что эти функции неплохо аппроксимируются логарифмически-нормальным распределением с заметными отклонениями от него в области малых значений рассматриваемой случайной величины, эмпирические вероятности которых оказываются больше, чем по логарифмически-нормальному распределению, так как к этим малым значениям при измерениях прибавляется инструментальный шум. В качестве примера на рис. 6 приводится гистограмма значений случайной величины
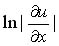 с аппроксимирующей эту гистограмму наилучшей (в смысле наименьшего квадрата отклонения) нормальной кривой.
с аппроксимирующей эту гистограмму наилучшей (в смысле наименьшего квадрата отклонения) нормальной кривой.
Обратим внимание также на заметную на рис. 1 заниженность эмпирических вероятностей больших значений
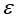 по сравнению с логарифмически-нормальным распределением. Она может создаваться недостаточным объемом выборки, по которой построена гистограмма: очень большие значения
по сравнению с логарифмически-нормальным распределением. Она может создаваться недостаточным объемом выборки, по которой построена гистограмма: очень большие значения
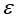 встречаются редко и в малой выборке могут и не встретиться. Тогда правый край гистограммы будет статистически неустойчивым, т. е. будет заметно меняться от выборки к выборке. Однако имеющиеся данные создают впечатление, что заниженность эмпирических вероятностей больших значений
встречаются редко и в малой выборке могут и не встретиться. Тогда правый край гистограммы будет статистически неустойчивым, т. е. будет заметно меняться от выборки к выборке. Однако имеющиеся данные создают впечатление, что заниженность эмпирических вероятностей больших значений
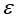 имеет систематический характер. Тогда для нее надо искать другое объяснение. Стюарт, Уилсон и Барлинг предлагают объяснять это отклонение от логарифмически-нормального распределения тем, что последнее должно достигаться лишь в пределе при больших п в (2.1) или
имеет систематический характер. Тогда для нее надо искать другое объяснение. Стюарт, Уилсон и Барлинг предлагают объяснять это отклонение от логарифмически-нормального распределения тем, что последнее должно достигаться лишь в пределе при больших п в (2.1) или
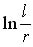 в схеме Новикова [4], так что для его достижения должно быть велико не только число Рейнольдса
в схеме Новикова [4], так что для его достижения должно быть велико не только число Рейнольдса
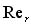 но и его логарифм ln
но и его логарифм ln
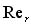 ; если же ln
; если же ln
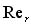 , а потому и число слагаемых в сумме (2.1) недостаточно велики, как это оказывается при реальных измерениях, то эта сумма будет принимать большие значения с меньшими вероятностями, чем по нормальному распределению.
, а потому и число слагаемых в сумме (2.1) недостаточно велики, как это оказывается при реальных измерениях, то эта сумма будет принимать большие значения с меньшими вероятностями, чем по нормальному распределению.
Вследствие заниженности эмпирических вероятностей больших значений
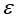 эмпирические моменты высоких порядков величины
эмпирические моменты высоких порядков величины
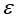 оказываются значительно меньше моментов логарифмически-нормального распределения. Это различие растет при увеличении порядка моментов.
Так, согласно неравенству Новикова, экспоненты
оказываются значительно меньше моментов логарифмически-нормального распределения. Это различие растет при увеличении порядка моментов.
Так, согласно неравенству Новикова, экспоненты
 для моментов коэффициента дробления растут не быстрее, чем линейная функция от порядка моментов q, а для моментов логарифмически-нормального распределения
для моментов коэффициента дробления растут не быстрее, чем линейная функция от порядка моментов q, а для моментов логарифмически-нормального распределения
 оказывается квадратичной функцией от q [заметим, что при таком быстром росте с q совокупность всех моментов не определяет однозначно распределение вероятности, и при наличии динамических уравнений начальные значения всех моментов не определяют однозначно их будущих значений, даже если динамическая задача в целом имеет единственное решение, в то же время неравенство Новикова гарантирует однозначное определение распределения вероятности по его моментам (2.5)]. В этом различии, конечно нет ничего удивительного, так как при
оказывается квадратичной функцией от q [заметим, что при таком быстром росте с q совокупность всех моментов не определяет однозначно распределение вероятности, и при наличии динамических уравнений начальные значения всех моментов не определяют однозначно их будущих значений, даже если динамическая задача в целом имеет единственное решение, в то же время неравенство Новикова гарантирует однозначное определение распределения вероятности по его моментам (2.5)]. В этом различии, конечно нет ничего удивительного, так как при
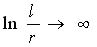 моменты коэффициента дробления вовсе не стремятся к моментам какого-то предельного распределения, а неограниченно возрастают (а конечный предел — нормальное распределение — имеется лишь у распределения вероятностей центрированного и нормированного логарифма коэффициента дробления).
моменты коэффициента дробления вовсе не стремятся к моментам какого-то предельного распределения, а неограниченно возрастают (а конечный предел — нормальное распределение — имеется лишь у распределения вероятностей центрированного и нормированного логарифма коэффициента дробления).
В качестве иллюстрации Новиков Е. А. [4] рассмотрел статистическую модель, в которой коэффициент дробления
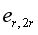 , значения которого образуют интервал 0<=у<=2, имеет в этом интервале постоянную плотность вероятности р(у) =1/2. Для этой модели
, значения которого образуют интервал 0<=у<=2, имеет в этом интервале постоянную плотность вероятности р(у) =1/2. Для этой модели

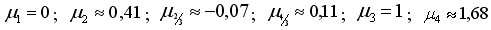 .
Характеристическая функция для
.
Характеристическая функция для
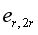 в этой модели равна
в этой модели равна
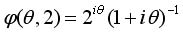 , так что
, так что
 Логарифмически-нормальное приближение получается при замене функции
Логарифмически-нормальное приближение получается при замене функции
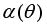 двумя первыми членами ее ряда Тэйлора
двумя первыми членами ее ряда Тэйлора
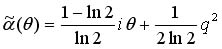 и дает моменты
и дает моменты
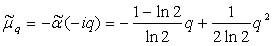 существенно отличающиеся от истинных моментов (2.4), причем это различие увеличивается с ростом q; в частности,
существенно отличающиеся от истинных моментов (2.4), причем это различие увеличивается с ростом q; в частности,
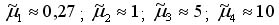 .
Далее, зная
.
Далее, зная
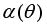 для логарифма любого коэффициента дробления
для логарифма любого коэффициента дробления
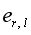 получаем характеристическую функцию
получаем характеристическую функцию
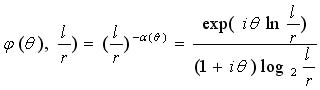
Итак, логарифмически-нормальное распределение завышает вероятности больших значений ? и старшие моменты этой случайной величины, но может быть использовано для описания центральной части распределения вероятности ? и для расчета младших моментов. Поэтому представляет интерес эмпирическая проверка, вытекающей из логарифмически-нормальной аппроксимации формулы
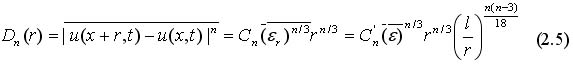
Множитель со степенью отношения L/r и возможность зависимости коэффициента
 от крупномасштабных особенностей движения представляют собой уточнения к предсказаниям обычной теории подобия Колмогорова, не учитывающей флюктуаций поля скорости диссипации турбулентной энергии.
от крупномасштабных особенностей движения представляют собой уточнения к предсказаниям обычной теории подобия Колмогорова, не учитывающей флюктуаций поля скорости диссипации турбулентной энергии.
Такая проверка была проделана по данным измерений пульсаций скорости течения в верхнем слое океана. Беляев, Монин и Озмидов [5] опубликовали спектры пульсации продольной скорости и' по данным, полученным на 10 полигонах в 9-м рейсе «Академика Курчатова» в 1971 г. и в 7-м рейсе «Дмитрия Менделеева» в 1972 г. По этим спектрам были определены соответствующие значения ?. Гистограмма и эмпирическая кривая интегрального распределения вероятности значений lg ? приведены на рис. 2 и 3.
Они неплохо аппроксимируются нормальным распределением с математическим ожиданием – 1,15 и стандартным отклонением 0,82.

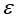 , аппроксимированная кривой закона нормального распределения.
, аппроксимированная кривой закона нормального распределения.

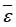 , аппроксимированная кривой закона нормального распределения.
, аппроксимированная кривой закона нормального распределения.