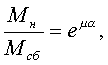
где
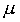- коэффициент сцепления,
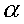- угол обхвата.
АВТОРЕФЕРАТ
магистерской работы Карпина Евгения Николаевича:
Тема: "Исследование системы фазового регулирования пуском асинхронного двигателя и разработка рекомендаций по применению её для мощных ленточных конвейеров"
Научный руководитель:
Корниенко Анатолий Прокофьевич,
старший преподаватель кафедры ЭАПУ.
СОДЕРЖАНИЕ
Конвейерный транспорт приобретает на открытых разработках Украины, а также ряда зарубежных стран всё возрастающее значение. Применение в карьерах конвейерного транспорта характеризуется ростом его параметрических показателей. Этому сопутствует изменение и усовершенствование конструкций конвейеров и постоянное появление новых конструктивных рашений. Поточный карьерный транспорт по достигнутой технико-экономической эффективности и в особенности по производительности труда во многих случаях превзошел другие виды карьерного транспорта или даёт в сочетании с ними высокие показатели по результатам эксплуатации.
При резко возрастающем значении в горной промышленности открытого способа добычи полезных ископаемых, росте производственной мощности горных предприятий и увеличении глубины разработок, а также создании мощного технологического оборудования непрерывного действия (в основном роторных экскаваторов) карьерный конвейерный транспорт во многих случаях уже сейчас является практически бесконкурентным. Перспективы дальнейшего развития карьерного конвейерного транспорта огромны, область его применения начинает распространяться не только на рыхлые, но и на скальные горные породы; правильное решение стоящих в этой области научных и инженерных задач имеет большое значение.
Между тем отечественная и зарубежная литература о системах электропривода мощных конвейерных установок весьма ограничена и состоит преимущественно из небольшого количества статей или глав в технических книгах. Поэтому в данной работе поставлена задача частично восполнить этот пробел.
Известно, что стоимость конвейерной ленты составляет около 90% от стоимости конвейера. Следовательно, запуск конвейера независимо от загруженности ленты должен быть плавным с ограниченным ускорением, чтобы предотвратить пробуксовку и часто возникающий приэтом пожар ленты. Это особенно важно для пуска конвейеров большой протяжённости, у которых кроме опасности пробуксовки существует опасность возникновения колебательного переходного процесса в сбегающей ветви ленты, который зачастую приводит к обрыву ленты. Отсюда можно сделать вывод, что необходима система электропривода с жёстким ограничением ускорения при пуске, и в то же время по относительно простой схеме, так как время пуска конвейеров намного меньше времени его работы на установившейся скорости. Система электропривода постоянного тока не нашла своего применения в силу специфических условий эксплуатации (запылённость, резкие колебания температур и др.). Всё чаще для мощных ленточных конвейеров применяется система электропривода с применением асинхронных двигателей с фазным ротором, управляемых по роторной цепи с помощью пуско-регулировочных устройств типа УПТФ. Однако и такая система имеет некоторые недостатки, о которых будет сказано ниже. Поэтому совершенствование такой системы является актуальным вопросом научных исследований в области электропривода конвейерных установок.
В настоящей работе ставится задача исследования динамических режимов мощных протяжённых ленточных конвейеров с двухбарабанным приводом, осуществляемым от асинхронных двигателей, управляемых по роторной цепи с помощью пуско-регулировочных устройств типа УПТФ. При этом целью исследований является определение законов управления и разработка технических решений, обеспечивающих наиболее благоприятные условия пуска конвейера при различных внешних воздействиях.
Протяжённые конвейеры представляют собой сложную механическую систему с распределёнными параметрами. Описание таких систем связано с применением нелинейных дифференциальных уравнений в частных производных, точное аналитическое решение которых во многих случаях недостижимо. Тем не менее динамические режимы, возникающие в процессе работы конвейеров, представляют большой практический интерес, поэтому ряд исследователей уделяют этому вопросу достаточно много внимания. Однако, все известные решения получены при тех или иных упрощающих допущениях. В частности, не изучены динамические режимы работы двухбарабанных конвейеров, привод которых осуществляется от серийно выпускаемых устройств УПТФ.
Слабо изучены в литературе и такие вопросы, как нахождение рационального распределения тяговых усилий между приводными барабанами, обеспечивающее их работу без пробуксовки; обеспечение равномерного распределения нагрузки между приводными двигателями как в статическом, так и в переходном режимах. Эта задача становится особенно важной при пуске с учётом распределённости параметров конвейеров.
МЕТОДИКА ПРОВЕДЕНИЯ ИССЛЕДОВАНИЙ
Исследования проводились путём математического моделирования системы параметрического регулирования в приложении SIMULINK пакета MATLAB. Далее полученные результаты моделирования проверялись на базе стенда УПТФ, расположенного в аудитории №105 8-го учебного корпуса ДонНТУ. Получены графики, близкие к результатам моделирования. Регистрация переходных процессов производилась электронно-лучевым осциллографом С1-67. В данной работе пока не имеется возможности представить полученные осциллограммы, но в дальнейшем предполагается снятие характеристик на запоминающий двухлучевой осциллограф С8-17. Эти результаты будут представлены в выпускной магистерской работе.
Новизна диссертации заключается в построении и отладке цифровой модели в пакете MATLAB, а также в практической реализации усовершенствования устройства УПТФ, заключающейся во внесении ряда изменений в принципиальную электрическую схему. До этого цифровая модель реализовывалась с помощью языка программирования Паскаль, который в настоящее время "морально" устарел.
ДИНАМИЧЕСКАЯ МОДЕЛЬ ЛЕНТОЧНОГО КОНВЕЙЕРА
Внешний вид ленточного конвейера представлен на рис.1.
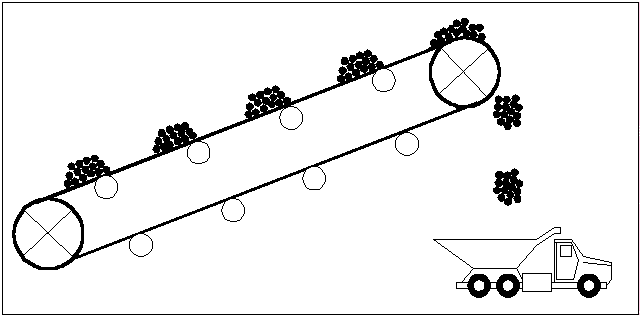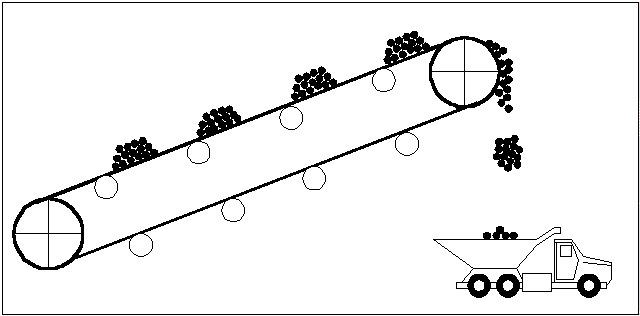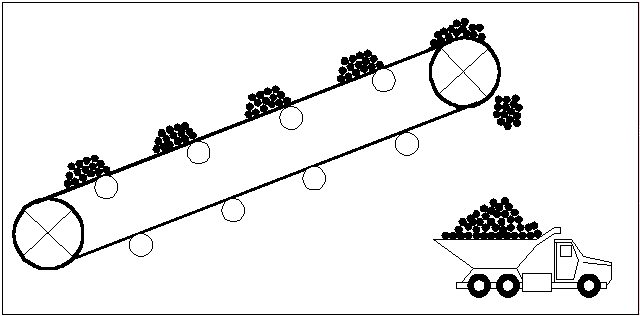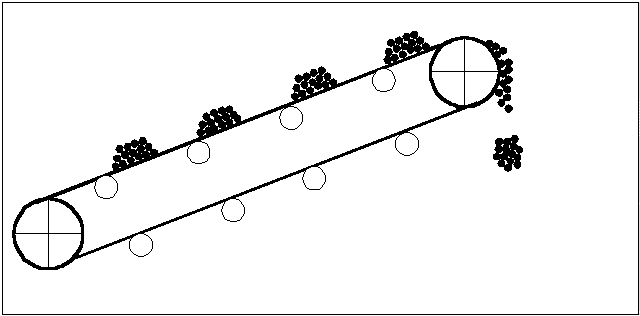
Рисунок 1 - Внешний вид ленточного конвейера
На основании данного рисунка можно составить расчётную схему конвейерной ленты с находящимся на ней грузом и поддерживающими её роликами. Для общности считается, что к барабанам приложены как реактивные силы, всегда направленные против движения и не способные самостоятельно вывести систему из равновесия, так и активные. Реактивные силы порождаются, в основном, силами трения, препятствующими движению ленты, а активные могут быть обусловлены либо гравитационной составляющей, для наклонных конвейеров, либо воздействием со стороны привода. В дальнейшем считается, что все моменты инерции и моменты сил сопротивления приведены к поступательному движению ленты. Основные особенности ленточных конвейеров, влияющие на режимы работы привода и определяющие требования к последнему могут быть установлены на основе анализа схемы, приведенной на рис. 2.
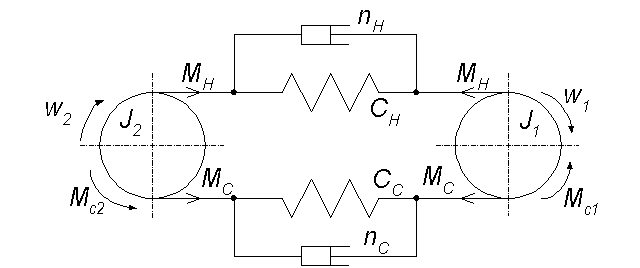
Рисунок 2 - Расчётная схема ленточного конвейера
На нём показан приводной барабан с моментом инерции J1, включающим также приведенные к его оси моменты инерции всех связанных с ним подвижных элементов привода. Маховик, имеющий момент инерции J2, имитирует конвейерную ленту, находящийся на ней груз и все связанные с лентой подвижные элементы. Причём, моменты инерции всех элементов, вошедших в J2, приведены к валу приводного барабана. Упругие свойства ленты учтены с помощью пружин, обладающих жёсткостями Cн - в набегающей ветви и Cс - в сбегающей. Диссипативные потери учитываются коэффициентами демпфирования nн и nс в набегающей и сбегающей ветвях соответственно. Маховики J1 и J2, пружины Cн и Cс связаны между собой невесомой абсолютно жёсткой гибкой нитью. Причём, скольжение нити по поверхности маховика J2 невозможно, в то время, как между приводным барабаном J1 и нитью связь осуществляется за счёт сил трения и при определённых условиях возможно возникновение взаимного проскальзывания. На расчётной схеме показаны частоты вращения маховиков w1 и w2, а также приложенные к ним моменты: Мн и Мсб - обусловленные силами натяжения набегающей и сбегающей ветвей конвейерной ленты, Мс1 и Мс2 - моменты сил сопротивления движению приводного барабана и конвейерной ленты соответственно, и М - момент, действующий на маховик со стороны электропривода.
Принебрегая электромагнитной постоянной времени и считая, что электропривод обладает линейной механической характеристикой с постоянной жёсткостью, можно записать систему уравнений, отражающих динамические режимы работы конвейера при отсутствии буксования:
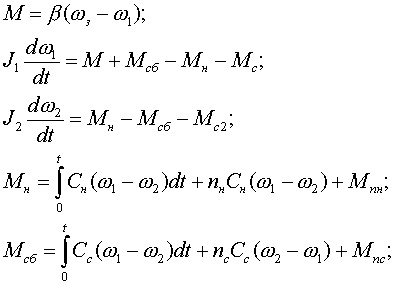
где wз - заданная частота вращения электропривода, Мпн и Мпс - моменты, обусловленные силами предварительного натяжения набегающей и сбегающей ветвей конвейера соответственно. Преобразование переменных, входящих в систему уравнений и характеризующих состояние конвейера и характеризующих состояние конвейера с электроприводом, наглядно отражает структурная схема, приведенная на рис.3.
В этой схеме введен новый параметр С=Сн+Сс - суммарный коэффициент жёсткости конвейерной ленты и новая переменная М12 - результирующий момент, обусловленный силами деформации обоих ветвей ленты конвейера.
Полученная структурная схема представляет собой хорошо изученную двухмассовую систему элетропривода с упругой связью. Однако, она не позволяет учесть возможность возникновения режима буксования, когда момент, передаваемый приводным барабаном ленте, достигает предельно допустимой величины, определяемой силами трения контактирующих поверхностей ленты и барабана.
Как известно, в режиме скольжения конвейерной ленты по поверхности приводного барабана выполняется условие
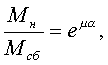
где 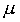- коэффициент сцепления,
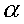- угол обхвата.
Выражение, записанное в виде соотношения
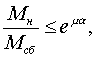
является условием разграничения режима работы конвейера без буксования, когда выражение принимает смысл неравенства; и режима буксования - когда смысл равенства. Полставляя в это выражение значения Мн и Мсб, можно получить
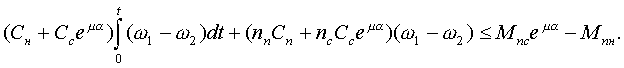
Как видно, соотношение оказывается достаточно громоздким и неудобным для использования в целях разграничения режимов работы конвейера с буксованием и без него, особенно на этапе предварительного анализа объекта управления. Гораздо проще эти условия формируются в том случае, если обе ветви конвейера являются симметричными, когда выполняются равенства
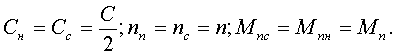
Наложение ограничений не изменяет общих динамических свойств системы, но позволяет существенно упростить данное соотношение, которое приобретает вид:
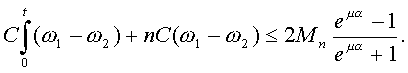
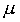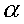В левой части этого соотношения стоит выражение, определяющее величину результирующего момента М12, обусловленного силами деформации конвейерной ленты, а в правой - постоянная величина, определяемая начальными условиями Мп и параметрами барабанного привода конвейера и . С учётом этого структурная схема объекта, позволяющая учесть возможность возникновения режима буксования, приобретает вид, показанный на рис. 4. Она позволяет в первом приближении отразить оба возможных режима работы конвейера - с буксованием и без него.
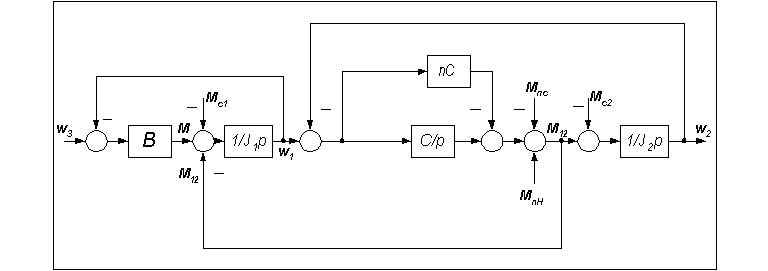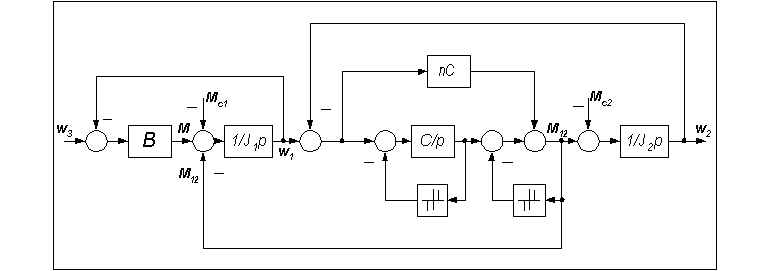
Рисунок 3 - Структурная схема конвейера без учёта и с учётом режима буксования
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЗАМКНУТОЙ СИСТЕМЫ ФАЗОВОГО РЕГУЛИРОВАНИЯ
В настоящее время широкое распространение получает электропривод конвейеров на основе асинхронных двигателей с фазным ротором, управление которыми при пуске осуществляется с помощью комплектных тиристорных устройств УПТФ. Силовая часть электропривода в них реализована в соответствии со схемой, показанной на рис. 4.
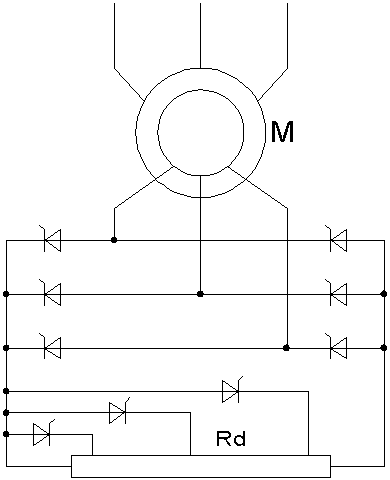
Рисунок 4 - Силовая часть схемы фазового управления асинхронным электродвигателем по роторной цепи
Плавное регулирование момента и скорости движения в этих условиях осуществляется за счёт изменения угла управления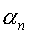 
тиристорным мостовым выпрямителем. Для повышения пусковых моментов и улучшения тепловых режимов электрической машины в цепь выпрямленного тока введён секционированный добавочный резистор Rd, величина которого может ступенчато изменяться с помощью ключевых тиристорных элементов, управляемых от специальной логической схемы.
Для расчёта механических характеристик электродвигателя в этой схеме разработан метод, основанный на интегральных оценках свойств тиристорного преобразователя, включенного в цепь ротора, которые позволяют при определённых допущениях осуществить его замену эквивалентным линейным двухполюсником, включение которого в схему замещения электрической машины позволяет распространить традиционные методы расчёта механических характеристик и на этот случай. Помимо общепринятых для таких расчётов допущений дополнительно вводим следующие: ЭДС ротора синусоидальна, коммутация идеальных вентилей происходит мгновенно. Для того, чтобы осуществить замену нелинейного тиристорного моста линейным двухполюсником, необходимо обеспечить их энергетическую эквивалентность. С этой целью, используя методы, изложенные в [14], находятся расчётные соотношения, позволяющие определить величины активной и реактивной мощностей, потребляемых тиристорным выпрямителем при различных углах управления с учётом принятых допущений.
Как известно, анализируемая схема управляемого выпрямителя имеет 2 режима работы: непрерывных токов при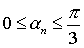 
и прерывистых токов при 
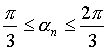. В результате получаются следующие расчётные соотношения, позволяющие определить величины сопротивлений эквивалентного двухполюсника:
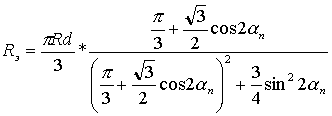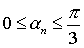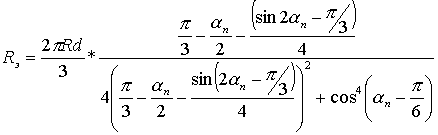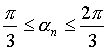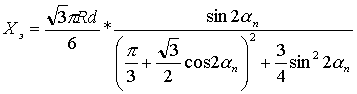при ,
при ;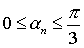
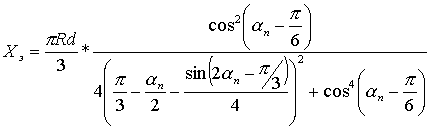при ,
при .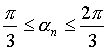
Полученные выражения позволяют по известным величинам угла управления 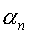и резистора Rd вычислить значения параметров цепи, эквивалентной по своему воздействию на свойства электродвигателя, тиристорному преобразователю, включенному в его роторную цепь. Тогда можно воспользоваться для расчёта механичесих характеристик машины традиционной формулой:
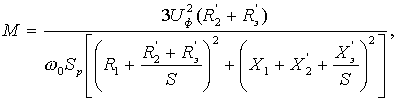
где w0 - частота вращения магнитного поля статора;
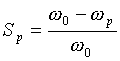- скольжение ротора;
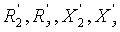- активные и реактивные сопротивления роторной цепи, приведенной к статору.
Для завершения математического описания замкнутой системы параметрического управления асинхронным приводным электродвигателем конвейера уже полученные расчётные соотношения необходимо дополнить уравнениями, характеризующими работу задатчика интенсивности (ЗИ), первого сумматора и СИФУ.
Выходное напряжение ЗИ подчиняется простой закономерности:
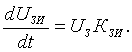
Для первого сумматора, формирующего напряжение управления, справедливо выражение:
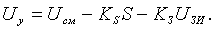
Коэффициент обратной связи по скольжению Ks должен выбираться из расчёта обеспечения требуемой жёсткости механических характеристик электродвигателя в замкнутой системе управления, а величины напряжения смещения Uсм и масштабного коэффициента Кз должны при этом обеспечить нормальное функционирование устройства во всех режимах работы.
Связь между углом управления 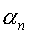на выходе ячейки СИФУ с его входным напряжением Uу устанавливается выражением:
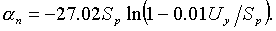
Разработанное математическое описание всех основных электрических и механических систем конвейера может служить надёжной основой для создания модели замкнутой системы параметрического регулирования, изображённой на рис. 5.
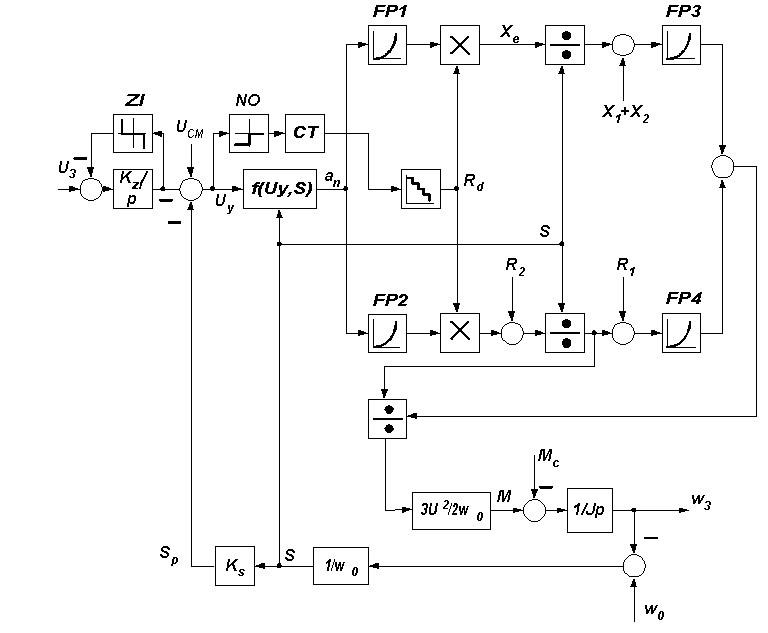
Рисунок 5 - Структурная схема замкнутой системы параметрического регулирования
На данной схеме приняты следующие обозначения:
ZI - задатчик интенсивности;
NO - нуль-орган, фиксирующий переход через 0 сигнала Uу;
СT - счётчик, вырабатывающий сигнал на шунтирование очередной ступени пускового реостата;
FP1 - FP4 - функциональные преобразователи.
АНАЛИЗ РЕЗУЛЬТАТОВ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Для моделирования системы электропривода конвейеров в приложении Simulink пакета MATLAB набирается составная структурная схема с учётом режима буксования, состоящая из рис. 3,5, т.е. выход wз подключается ко входу wз. На рис. 6 изображены графики переходных процессов при пуске протяжённого магистрального конвейера. На графиках можно увидеть одну неблагоприятную особенность, заключающуюся в том, что моменты шунтирования пускового резистора сопровождаются кратковременными пиковыми выбросами момента. Это неблагоприятно сказывается как на работе мехенической части оборудования, так и на самом электродвигателе и устройстве УПТФ,
и может привести к срыву сцепления ленты с барабаном, а также дальнейшему выходу из строя электродвигателя вследствие тряски обмоток ротора.
Дополнительный анализ процессов, происходящих в период пуска, показал, что сигналы на шунтирование очередных секций пускового резистора формируются при полностью открытом тиристорном выпрямителе находящемся в роторной цепи двигателя. По этой причине единственным фактором, ограничивающим величину тока ротора, а следовательно и момента, является пусковой резистор, который скачкообразно уменьшается, что и приводит к всплеску тока и момента. В последующем за счёт подразгона двигателя и действия обратной связи происходит увеличение угла управления тиристорами выпрямителя, что приводит к ограничению тока и момента на необходимом уровне.
Из вышесказанного следует, что имеется возможность полностью устранить всплески момента, если несколько изменить процессы, протекающие в устройстве УПТФ. Эти изменения заключаются в следующем: при возникновении сигнала о необходимости шунтирования очередной системы пускового резистора следует предварительно произвести подзапирание тиристорного выпрямителя и только после этого осуществлять коммутацию пускового резистора.
Наиболее просто реализовать высказанные предложения за счёт формирования напряжения задатчика интенсивности ступенчатой формы. При этом в момент формирования сигнала об очередном шунтировании ступени пускового реостата необходимо скачкообразно осуществлять снижение уровня выходного сигнала ЗИ, что автоматически приведёт к подзапиранию выпрямителя, а следовательно и в устранении всплеска тока ротора при последующем шунтировании пусковой ступени.
Соответствующие результаты переходных процессов приведены на рис. 6.
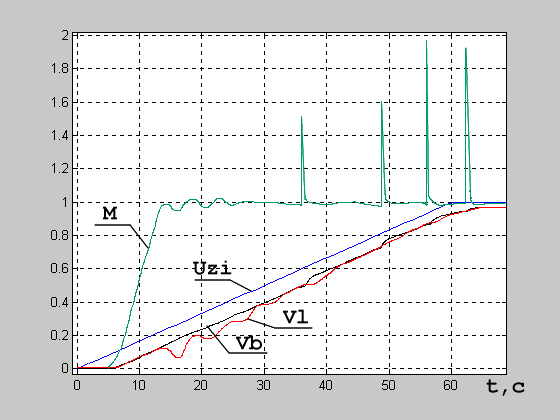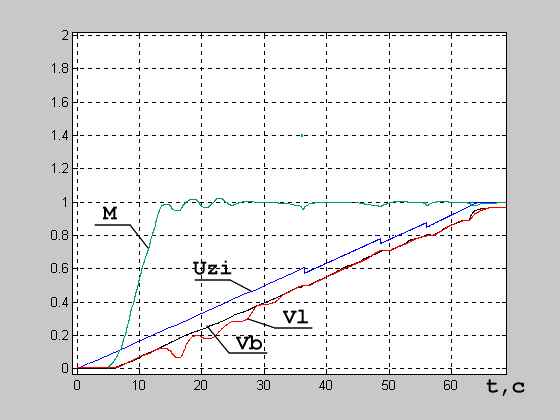
Рисунок 6 - Переходные процессы при пуске ленточного конвейера от стандартного устройства УПТФ и от модернизированного устройства
На графиках введены следующие обозначения (значения величин - в относительных единицах по отношению к номиналу):
М - момент приводного двигателя;
Uzi - напряжение задатчика интенсивности (ЗИ);
Vb - линейная скорость приводного барабана конвейера;
Vl - скорость ленты.
ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ ИССЛЕДОВАНИЙ
Исходя из всего вышеизложенного и уже имеющихся схематических решений, принятых в устройстве УПТФ, необходимо осуществить разработку блока, который будучи подключен к УПТФ позволил бы формировать ступенчатое изменение сигнала на выходе ЗИ.
Кроме того, во избежание переключений ступеней пускового реостата в неконтролируемые моменты работы тиристорного выпрямителя, проектируемое устройство должно обеспечить выдачу сигнала на тиристорные ключи пускового реостата синхронно с импульсами управления тиристоров мостового выпрямителя.
Таким образом, блок подавления пиков момента должен содержать в себе 2 узла: узел синхронизации, обеспечивающий разрешение шунтирования очередной секции пускового реостата в моменты выдачи управляющих импульсов на тиристоры мостового выпрямителя и узел коррекции выходного напряжения ЗИ. В данной плате применяются только распространённые элементы, включенные во относительно простой схеме, что позволило реализовать данный блок самостоятельно. Результаты переходных процессов можно оценить с помощью любого электронно-лучевого осциллографа. В данном случае применялся осциллограф С1-67 и, как было сказано выше, получены результаты, близкие к полученным с помощью математического моделирования, что свидетельствует об адекватности математической модели протекаемым процессам. К сожалению, в данной работе нет возможности привести полученные осциллограммы.
Выполнение экспериментальных исследований осуществлялось на специально собранной установке. Её функциональная схема приведена на рис. 7.
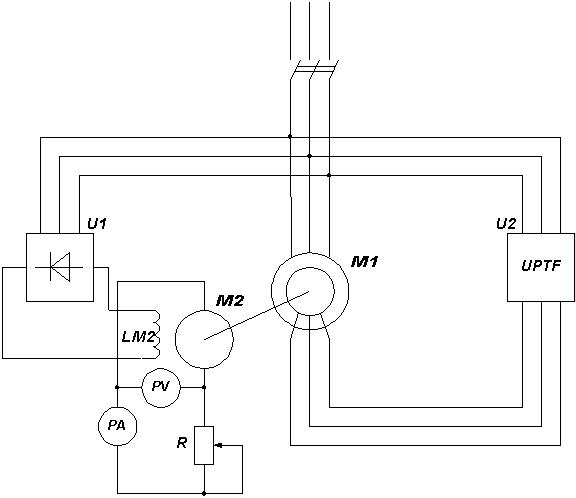
Рисунок 7 - Функциональная схема экспериментальной установки
В состав установки входят исследуемый асинхронный электродвигатель с фазным ротором М1 типа АК-60-4 и связанная с ним общим валом нагрузочная машина постоянного тока М2 типа П-21. Исследуемый двигатель управляется устройством U2 типа УПТФ-630. Нагрузочная машина М2 включена по схеме динамического торможения. Её обмотка возбуждения получает питание от неуправляемого выпрямителя U1. Для изменения величины нагрузочного момента исследуемой машины служит реостат R. Экспериментальная установка позволяет исследовать как статические, так и динамические режимы асинхронной машины, управляемой с помощью устройства типа УПТФ.
В результате проделанной работы рассмотрены следующие вопросы:
Не решены такие вопросы, как: