Кремешная Ольга Александровна Тема: "Разработка компьтеризированной системы сжатия информации, полученной в результате научных экспериментов, для долговременного хранения" Руководитель: доцент, к.т.н. Орлов Юрий Константинович E-mail: kremeshnaya@ukrtop.com

Обоснование темы и ее актуальность

В настоящее время объемы информации, подлежащей хранению, имеют устойчивую тенденцию роста. Для хранения таких объемов информации необходимо ее предварительное сжатие с последующей возможностью восстановления и обработки.

В последнее время особенно актуальными стали исследования метеорологических и климатических процессов [3]. При этом возрастает как объем обрабатываемых данных, так и сложность моделируемых процессов.

Так, например, сейчас происходит мощное стойкое концентрирование загрязняющих веществ в поверхностном слое Мирового океана, что существенно отражается на изменении основных физических параметров и океана и атмосферы: температуре, вязкости, солености, поверхностном натяжении, солнечной радиации и т.д.

Мировой океан - аккумулятор и распределитель тепла, получаемого от солнца. Если его поверхностный слой отравлен и загрязнен, он не может правильно выполнять свои функции по поддержанию теплового режима, круговорота воды и других сложнейших механизмов жизни на Земле. Естественно, нарушаются и все химические, биологические, гидрофизические процессы в самом океане. Поэтому актуальной задачей становится не только анализ и мониторинг экологического состояния мирового океана, а и прогноз наиболее вероятной будущей ситуации.

Атмосфера и океан не имеют государственных границ, поэтому в гидрометеорологии очень сильно развито международное сотрудничество. Необходима унификация системы наблюдения за состоянием окружающей среды, обмен данными.

Мировой океан - это место сосредоточения важнейших видов хозяйственной, военной и научно-технической деятельности разных государств, транснациональных корпораций, международных организаций и, одновременно, место пересечения их интересов. В связи с этим использование информации о состоянии мирового океана и прибрежных территорий в виде гидрометеорологических, гидрографических, ледовых, гидробиологических, морских геолого-геофизических и других данных информационной продукции является неотъемлемым элементом морской деятельности, что, в свою очередь, определяет повышенное внимание к проблеме формирования и ведения соответствующих информационных ресурсов.

Международный опыт организации Глобальной системы наблюдения океана (GOOS) показал, что GOOS стоит создавать как интегрированную наблюдательно - информационную систему на основании существующих регионально-национальных морских систем наблюдения на модульном принципе.

Способ ведения длительных наблюдений за состоянием среды является наиболее важным с точки зрения оценок вариаций режима и климата. Традиционный способ исследования режима и климата океана в повторяющихся точках на стандартных разрезах обеспечивает сравнимость результатов наблюдений по многогодовым рядам.

Данные задачи невозможно реализовать без предварительного сжатия данных, полученных в результате исследований, для их последующего хранения, что подтверждает актуальность данной работы.

Обзор состояния исследований по теме

Проблема единообразного (в смысле применяемого аппарата) и достаточно простого (в смысле реализации) представления сложных функций многие века занимала математиков. В ушедшем столетии этой проблемой занялись и представители прикладных наук, в частности, таких как связь, радиотехника и средства телекоммуникаций. Можно отметить такие крупные вехи на пути решения этой проблемы, как разложение произвольных (с определенными ограничениями) функций в ряд Тейлора, полиномиальную и рациональную аппроксимации и, наконец, представление функций и сигналов рядами Фурье.

В последние годы стало очевидно, что традиционный аппарат представления произвольных функций и сигналов в виде рядов Фурье (или Фурье-представлений) оказывается малоэффективным для функций с локальными особенностями, в частности для импульсных и цифровых сигналов и изображений, получивших весьма широкое распространение. Это связано с тем, что базисная функция рядов Фурье - синусоида определена на всей временной оси и по своей природе является гладкой и строго периодической функцией. Как об этом говорили ниспровергатели рядов Фурье, такая функция на практике (в условиях ограничения числа членов ряда или спектра разложения) не способна описывать произвольные сигналы и функции.

Таким образом, известные методы представления сигналов и функций постоянно наталкивались на теоретические ограничения, не позволяющие всерьез говорить о решении проблемы единообразного представления функций и сигналов (особенно нестационарных) методами, созданными на основе средств преобразований Фурье. Открытие вейвлетов, похоже, наконец решило эту сложнейшую и актуальную научную проблему. Основой этого решения стала разработка принципиально нового базиса и класса функций, которые используются для декомпозиции и реконструкции функций и сигналов - в том числе нестационарных. Соответственно был создан и новый аппарат представления функций и сигналов, а уже совсем недавно инструментальные и программные средства, необходимые для его реализации.

Поистине неисчерпаемы возможности вейвлетов в обработке сигналов и изображений, например для Интернета с его ограниченной пропускной способностью каналов передачи информации, или в минимизации объема звуковых и видеофайлов. Популярные стандарты MP4, JPEG 2000 и известные графические программные средства Corel DRAW 9/10 уже широко используют вейвлет-технологию обработки изображений. Она включена и в расширения новейших систем компьютерной математики (СКМ), таких как MATLAB, Mathcad, Mathematica. Появились также микросхемы для вейвлет-преобразований.

Вейвлеты и основанные на них интегральные преобразования были предложены в начале 90-х годов ХХ века (хотя первый простейший тип вейвлета, по существу, был описан Хааром еще в 1909 году) и в последующее время интенсивно развивались. Наибольший вклад в разработку теоретических основ вейвлетов внесли Мейер, Добеши, Малл и другие ученые, опубликовавшие первые теоретические работы в этом направлении и сумевшие донести их до широкой общественности. К настоящему времени за рубежом в области вейвлет-преобразований опубликованы сотни книг, а число статей исчисляется многими тысячами. К сожалению, интерес к вейвлетам у нас резко активизировался лишь в последние годы.

Цель и задачи работы

Целью работы является разработка компьютеризированной системы сжатия информации с возможностью ее последующего восстановления с минимальными потерями.

Для достижения данной цели были поставлены следующие задачи:

• рассмотреть существующие методы сжатия информации;
• изучить возможности вейвлетов;
• проанализировать используемый математический аппарат;
• выбрать оптимальное дерево декомпозиции для представления исследуемых зависимостей.

Научная новизна и практическая ценность работы

В настоящее время вейвлет-технология используется графическим программным средством Corel Draw 9/10, стандартами MP4, JPEG 2000; включена в расширения систем компьютерной математики MATLAB, Mathcad, Mathematica. Однако отсутствуют программные продукты, которые позволяли бы практически применять данную технологию для сжатия экспериментальных данных.

Разработка компьютеризированной системы на базе вейвлетов позволит достичь наиболее эффективного сжатия данных и минимизировать потерю информации при восстановлении.

Применение вейвлетов для сжатия информации

Вейвлеты - это обобщенное название особых функций, имеющих вид коротких волновых пакетов с нулевым интегральным значением и с той или иной, подчас очень сложной, формой, локализованных по оси независимой переменной (t или x) и способных к сдвигу по ней и масштабированию (сжатию/растяжению) [1].

Вейвлеты создаются с помощью специальных базовых функций - прототипов, задающих их вид и свойства и удовлетворяющих целому ряду специфических условий. Набор вейвлетов, в их временном или в частотном представлении, может приближать сложный сигнал или изображение, причем идеально точно или с некоторой погрешностью.

Вейвлеты по существу являются новыми математическими понятиями и объектами, применение которых может теоретически строго и впрямь приблизить любую функцию и любой сигнал. Поэтому они весьма перспективны в решении многих математических задач приближения (интерполяции, аппроксимации, регрессии и т.д.) функций, сигналов и изображений [1-4]. Вейвлет-обработка сигналов обеспечивает возможность весьма эффективного сжатия сигналов и их восстановления с малыми потерями информации, а также решение задач фильтрации сигналов. Таким образом, вейвлеты пополняют набор традиционных средств обработки сигналов и изображений.

Вейвлет-спектограммы намного более информативны, чем обычные Фурье-спектограммы и (в отличие от последних) позволяют легко выявлять тончайшие локальные особенности функций, сигналов и изображений. Это полезно при решении задач идентификации сигналов и образов в картографии, в разведке полезных ископаемых, в медицине и даже в судебном делопроизводстве (одно из первых полезных применений вейвлетов связано с сильной компрессией изображений отпечатков пальцев без заметной потери информации).

Вейвлеты открывают новые и необычные подходы по сокращению избыточности и в очистке сигналов и изображений от шума. Суть одного из таких подходов заключается просто в ограничении уровня детализирующих коэффициентов. При этом возможно как глобальное ограничение всех коэффициентов по уровню, так и локальное ограничение. Более того, возможны разные типы порогов ограничения, например, мягкий в виде вертикальной ступеньки передаточной характеристики ограничения или жесткий в виде дополнительных горизонтальных полочек.

На практике, при сжатии данных или очистке сигналов от шума почти всегда имеют дело только с частотными фильтрами. За счет выбора оптимального дерева для данного сигнала или класса сигналов иногда можно существенно (в несколько раз) повысить эффективность сжатия. Для выбора оптимального (или квазиоптимального) дерева разработан ряд методов. Некоторые из них основаны на введении понятия энтропии, позволяющей оценить информативность набора коэффициентов.

Функция стоимости на основе понятия энтропии М имеет различные значения. Она большая, если вейвлет-коэффициенты получаются примерно одной величины, и мала, если они существенно отличаются. Это значит, что любое усреднение коэффициентов увеличивает энтропию. Функция стоимости должна быть аддитивной, что для сигнала x=s означает следующее:

М(0)=0



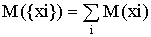
Под энтропией обычно понимается величина:

, где .

При этом используется следующая стратегия: сначала строится полное дерево разложения, затем снизу вверх анализируются пары узлов, имеющих общий корень. Если при переходе от корня к узлам энтропия не уменьшается, эта пара заменяет корень. Возможен упрощенный вариант - это подобрать оптимальный уровень, т. е. высоту полного дерева, при которой энтропия минимальна.

Выводы

По своей значимости роль вейвлетов можно сравнить разве что с выдающейся ролью рядов Фурье и преобразований Фурье. Как известно, именно ряды и преобразования Фурье при всех их, известных и обнаруженных уже в наше время и ранее, недостатках, легли в основу многих новых и ведущих областей науки и техники, начиная от решения дифференциальных уравнений различных классов, создания теоретических основ современной электротехники, радиотехники и всевозможных средств связи и телекоммуникаций и кончая многочисленными физическими и измерительными приборами на их основе (анализаторы спектра, синтезаторы сложных сигналов по гармоникам и др.).

Но вейвлеты имеют явные преимущества перед рядами Фурье как в общем и точном представлении функций, так и их разнообразных локальных особенностях. Они представлены намного более разнообразным набором типов, чем единственная синусоидальная функция в рядах Фурье. Это разнообразие вейвлетов с одной стороны резко расширяет круг решаемых с их помощью прикладных задач, а с другой стороны делает такое решение творческим.

Благодаря этим свойствам вейвлетов, их использование при разработке системы сжатия информации, полученной в результате экспериментальных исследований, является наиболее перспективным.

Литература

1. В.П. Дьяконов. Вейвлеты. От теории к практике. М.: СОЛОН-Р, 2002. 448 с.
2. К. Чуи. Введение в вейвлеты. Пер. с англ. под ред. Я.М. Жилейкина. М.: Мир, 2001.
3. Н.М. Астафьева. Вейвлет-анализ: основы теории и примеры применения. Успехи физических наук, т. 166, № 11, 1996.
4. С.А. Терехов. Вейвлеты и нейронные сети. Лекция для школы-семинара "Современные проблемы нейроинформатики". МИФИ, Москва, 24-26 января 2001 г.