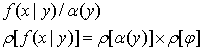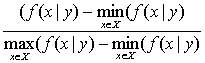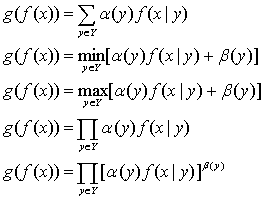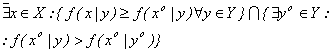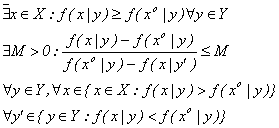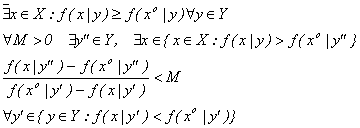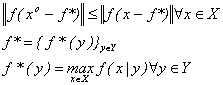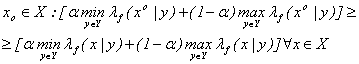Написать мне
Николай Николаевич Шоробура
Тема магистерской работы: "Разработка моделей и программных средств для многокритериальной оптимизации сложных объектов в компьютерных информационных системах"
Руководитель: доцент кафедры АСУ Лаздынь Сергей Владимирович
| На главную | Полезные ссылки | Библиотека | Индивидуальное задание |
|Отчет о поиске|
Введение.
1. Постановка задачи многокритериальной оптимизации.
2. Некоторые сведения.
3. Некоторые методы многокритериальной оптимизации.
3.1. Принцип справедливого компромисса.
3.2. Принцип слабой оптимальности по Парето.
3.3. Принцип приближения по всем локальным критериям к идеальному решению.
3.4. Метод квазиоптимизации локальных критериев (метод последовательных уступок).
3.5. Метод свертывания векторного критерия в суперкритерий.
4. Применение генетических алгоритмов для решения задач многокритериальной оптимизации.
5. Обощение результатов научного поиска и анализа.
5.1. Существующие проблемы многокритериальной оптимизации.
5.2. Возможные пути решения проблем многокритериальной оптимизации.
5.3. Выбор направления дальнейших исследований и предложения по структуре магистерской работы.
Список использованных источников.
Методы решения задач математического программирования с одним критерием интенсивно разрабатывались последние 40 лет. Изучение таких методов, однако, отражало самый ранний и простой этап в развитии математического программирования. Жизнь оказалась значительно сложнее. По мере того как мы постепенно вступаем в век информатики, становится ясно, что практически любая серьезная реальная задача характеризуется больше чем одним критерием. Лица, принимающие решения (ЛПР), в значительно большей степени, чем когда бы то ни было, ощущают необходимость оценивать альтернативные решения с точки зрения нескольких критериев.
Результаты исследования задач планирования и управления показывают, что в реальной постановке эти задачи являются многокритериальными. Так, часто встречающееся выражение «достичь максимального эффекта при наименьших затратах» уже означает принятие решения при двух критериях. Оценка деятельности предприятий и планирования как системы принятия решений производится на основе более десятка критериев: выполнение плана производства по объему, по номенклатуре, плана реализации, прибыли по показателям рентабельности, производительности труда и т. д.
Ранее, при исследовании проблемы многокритериальности часто все критерии, кроме одного, выбранного доминирующим, принимались в качестве ограничений, оптимизация проводилась по доминирующему критерию. Такой подход к решению практических задач значительно снижает эффективность принимаемых решений. В связи с этим в данной работе приводится общая постановка задачи многокритериальной (векторной) оптимизации планирования и некоторые основные подходы к ее решению.
Впервые проблема оптимизации векторного критерия была сформулирована экономистом Парето в 1896 г.
В задачах математического программирования с одним критерием нужно определить значение целевой функция, соответствующее, например, минимальным затратам или максимальной прибыли. Однако, немного подумав, мы практически в любой реальной ситуации обнаружим несколько целей, противоречащих друг другу.
Покажем, насколько широк диапазон проблем, которые могут быть адекватно сформулированы как многокритериальные, и какие характеристики следует использовать в качестве критериев.
Планирование очистки нефти
min {затраты},
min {количество импортируемой сырой нефти},
min {количество сырья с высоким содержанием серы},
min {отклонения от заданного состава},
min {сгорание газов}.
Планирование производства
mах {суммарный чистый доход},
mах {минимальный чистый доход за любой период},
min {число невыполненных заказов},
min {сверхурочное время},
min {запасы готовой продукции}.
Выбор портфеля ценных бумаг
mах {доход},
min {риск},
mах {дивиденды},
min {отклонения от желаемого уровня разнообразия бумаг}.
Составление сметы капиталовложений
mах {наличие средств},
min {спрос на капитальные вложения},
min {ежегодные эксплуатационные расходы},
max {инвестиции в проекты, связанные с охраной окружающей среды},
max {инвестиция в проекты в заданном регионе},
max {инвестиции в проекты по заданной товарной специализации}.
Управление лесным хозяйством
max {устойчивый урожай древесины},
max {человеко-дни отдыха в лесу},
max {человеко-дни охоты в лесу},
max {ареал распространения диких животных},
max {число месяцев выпаса домашних животных},
min {превышения бюджета}.
Управление попусками водохранилищ
max {выгоды от рекреации на водохранилище № 1},
max {выгоды от зарегулирования стока ниже водохранилища № 1},
max {количество энергии, вырабатываемой в бассейне реки},
min {недопоставки воды на коммунальные нужды в бассейне реки},
max {выгоды от рекреации на водохранилище № 2},
max {прибыль от орошения земель ниже водохранилища № 2}.
Формирование ревизионной службы в фирме
max {доход},
min {рост численности персонала службы},
min {уменьшение численности персонала службы},
min {избыточные сверхурочные},
min {недоиспользование квалификации кадров},
max {время, отведенное на профессиональный рост}.
Транспортировка
min {стоимость},
min {среднее время доставки грузов приоритетным клиентам},
max {производство по заданной технологии},
min {расход топлива}.
Изготовление смеси для сосисок, копченой колбасы и салями
min {стоимость},
min {жирность},
min {отклонение от требуемого цвета},
max {протеин},
min {отклонения от требуемого содержания влаги},
min {отклонения от требуемой пропорции свинины и говядины}.
Таким образом, для эффективного решения любой из данных задач необходимо в первую очередь построить многокритериальную математическую модель, которую затем нужно оптимизировать, предварительно выбрав наиболее подходящий для этого метод.
1. Постановка задачи многокритериальной оптимизации.
Задача многокритериального математического программирования имеет вид:
max{f1(x)=F1},
X – множество допустимых значений переменных х;
max{f2(x)=F2},
...
max{fk(x)=Fk}, при xєX, где
k – число целевых функций (критериев);
Fi – значение i-го критерия (целевой функции),
“max” – означает, что данный критерий нужно максимизировать.
Заметим, что по существу многокритериальная задача отличается от обычной задачи оптимизации только наличием нескольких целевых функций вместо одной.
При наличии в многокритериальной задаче критериев с разной размерностью с целью устранения данной проблемы используют нормализацию критериев. Способы нормализации представлены в таблице 2.1.
Таблица 2.1. Способы нормализации.
Нормализация Математическое выражение Сведение к безразмерным величинам Приведение к одной размерности Смена ингридиента Естественная нормализация Нормализация сравнения Нормализация Савиджа Нормализация осреднения
В данной таблице y – элемент пространства G. G – пространство элементов произвольной природы, называемых целевыми термами (в конкретных интерпретациях это совокупность, перечень или нумерация качественных свойств) элементов xєX.
Сверткой компонент многоцелевого показателя fєF называется отображение gє{F->R1}, которое преобразует совокупность компонент многоцелевого показателя f, соответствующих целевым термам yєY, в скалярный целевой показатель g(f(x|y)= g[{f(x|y}yєY]єR1. Основными видами сверток являются линейные, минимизационные, максимизационные, произведения и функции Кобба-Дугласа вида:
Проблемы получения и обоснования выбора сверток составляют основное направление теории полезности.
К настоящему времени сформулированы основные принципы выбора, приведенные в таблице 2.2.
Таблица 2.2. Принципы выбора.
Принцип выбора Условие оптимальности Доминантности Частичной доминантности Парето Слейтера Собственно эффективности Джерри Несобственно эффективности Джерри Равенства Суммарной эффективности Нэша Компромисса Доминирующего результата Гарантированного результата Наименьшего уклонения ламбда-критерия альфа-критерия Гурвица Максимума функции неопределенности
В задачах выбора решения, формализуемых в виде модели векторной оптимизации, первым естественным шагом следует считать выделение области компромиссов (или решений, оптимальных по Парето).
Вектор называется оптимальным по Парето решением, если не существует хєХ такого, что выполнены неравенства
и
Областью компромиссов Гх называется подмножество допустимого множества решений Х, обладающего тем свойством, что все принадлежащие ему решения не могут быть улучшены одновременно по всем локальным критериям — компонентам вектора эффективности. Следовательно, для любых двух решений, принадлежащих области Гх(х', x''єГх ), обязательно имеет место противоречие хотя бы с одним из локальных критериев. Это автоматически приводит к необходимости проводить выбор решения в Гх на основе некоторой схемы компромисса, что и послужило причиной для названия этого подмножества областью компромиссов.
Оптимальное решение, выбираемое на основе многокритериального подхода независимо от избираемого принципа оптимальности, всегда должно принадлежать области компромиссов. Иначе оно может быть улучшено и, следовательно, не является оптимальным. Таким образом, область компромиссов есть область потенциально оптимальных компромиссов. Отсюда следует, что при выборе решения по векторному критерию эффективности можно ограничить поиск оптимального решения областью компромиссов Гх, которая, как правило, значительно уже всей области возможных решений Х.
3. Некоторые методы многокритериальной оптимизации.
3.1. Принцип справедливого компромисса.
Пусть все локальные критерии, образующие вектор эффективности, имеют одинаковую важность.
Справедливым будем считать такой компромисс, при котором относительный уровень снижения качества по одному или нескольким критериям не превосходит относительного уровня повышения качества по остальным критериям (меньше или равен).
Этому принципу можно дать следующую математическую интерпретацию. Пусть в области компромиссов Гх даны два решения х’ и х’’, качество которых оценивается критериями F1(х) и F2(х). Решение х' превосходит решение х’’ по критерию F1, но уступает ему по критерию F2. Необходимо сравнить эти решения и выбрать наилучшие на основе принципа справедливого компромисса.
Для сравнения этих решений на основе принципа справедливого компромисса введем меру относительного снижения качества решения по каждому из критериев – цену уступки x:
(3.1)
гдеи
— абсолютные снижения уровня критериев при переходе от решения х' к решению х'' (для критерия F1) и при обратном переходе (для критерия F2).
Если относительное снижение критерия F1 больше, чем критерия F2, то следует отдать предпочтение решению х'. Это следует из сравнения цены уступки по каждому критерию.
Алгоритм решения задачи векторной оптимизации, основанный на принципе справедливого компромисса, включает следующие шаги.
Шаг 0. Выбираем х' и х’’є Dx.
Шаг 1. Вычисляем по формулам (3.1) х1 и х2.
Шаг 2. Если х1>х2, то выбираем х', если х1<х2. то выбираем х2.
Шаг 3. Если не существует вектора хєX предпочтительнее xI или xII, то решение останавливается, иначе выбираем новый вектор xIII и переходим к шагу 1.
Модель определения области компромиссов, а также модель справедливого компромисса инвариантны к масштабу измерения критериев. Однако первая из них является вспомогательной при выборе решения, а другая может быть использована только в тех ситуациях выбора решения, для которых идея справедливого компромисса может быть оправдана. Поэтому в большинстве случаев приходится прибегать к иным принципам оптимальности, имеющим смысл только в случае нормализованного пространства критериев, когда все локальные критерии имеют единый масштаб измерения. Однако в большинстве случаев масштабы измерения критериев неодинаковы, и возникает необходимость проводить нормализацию критериев, т. е. искусственно приводить их к единой мере.
Большинство принципов нормализации основывается на введении идеального решения, т. е. решения, обладающего идеальным вектором эффективности Fи. Это идеальное решение можно априорно предположить исходя из информации об объекте, а можно решить задачу оптимизации для каждого локального критерия и соответствующее этим решениям значение вектора эффективности принять за идеальный вектор эффективности Fи. Тогда выбор оптимального решения становится равнозначным наилучшему приближению к этому идеальному вектору Fи = (Fи , … , Fиn) В этом случае вместо действительного значения критериев рассматриваются или их отклонение от идеального значения
dFj=Fиj - Fj (3.2)
или их безразмерное относительное значение
(3.3)
При решении данной проблемы используются оба способа нормализации. Таким образом, успешное решение проблемы нормализации во многом зависит от того, насколько точно и объективно удается определить идеальное качество решения.
После нормализации критериев эффективности задача выбора решения приобретает ясный математический смысл. В теоретико-множественном отношении она становится задачей упорядочивания ограниченных векторных множеств, а с точки зрения теории приближений – задачей приближения в метрическом конечномерном пространстве. Это дает возможность проводить обоснованный выбор принципов оптимальности и выявлять их логический смысл.
Итак, для данного случая принцип оптимальности идентичен принципу приближения, а обобщенный скалярный критерий оптимизации – критерию приближения, являющемуся некоторой функцией отклонения от идеальной функции.
3.2. Принцип слабой оптимальности по Парето.
Вектор х1єХ называется слабо оптимальным по Парето решением (оптимальным по Слейтеру), если не существует вектора х1єХ, такого, что
Пусть xoj (i=1,m) есть оптимальные решения для обычных скалярных оптимизационных задач, каждая из которых максимизирует компоненту Fi(х) вектора F (х):
(3.4)
Если они являются максимальными решениями для каждой i, то считаем, что Fj(xoj) >Fi(xj) (i=1,m), где xoj — оптимальное решение задачи (3.4).
Положим, что Soj изображает множество решений, каждое из которых соответствует компоненту Fj, и
Soj = {x|Fj(x)?<=Fj(xoj)+aj} (3.5)
где aj представляет допустимое количество ограничений соответствующей области по отношению к Fj. Тогда оптимальное достаточное решение это такое решение, при котором минимальный компонент (наихудший компонент) максимизируется на множестве, удовлетворяющем достаточному условию хєХ и хєSo1nSo2n…,Som. Оно может быть сформулировано как
max z (3.6)
х, z при
Fj(x)>=z; (3.7)
Fi(x)>=Fj(x)oj—aj, i=1,m; (3.8)
хєХ. (3.9)
Здесь задача (3.6) – (3.9) неразрешима, если аj не настолько велико, что пересечение {S°j} непусто. Величины аj должны быть определены на основе значений Fj(xoj) или анализа точности. Можно доказать, что оптимальное решение задачи (3.6) – (3.9) есть оптимальное решение по Парето.
Алгоритм решения задачи имеет следующие этапы.
Шаг 1. Полагаем l=1 и решаем задачу
max z (3.10)
х, z при
Fj(x)>=z;
Fi(x)>=Fj(x)oj—aj, i=1,m; хєХ.
Вызываем исходное решение x1 и оцениваем целевую функцию F(x1).
Шаг 2. Когда хl задано, разлагаем F(хl) на удовлетворительные и неудовлетворительные
компоненты. Обозначим их соответственно через Sl иl.
Если Sl , тогда эта задача считается неразрешимой, а если Sl, то х1 — оптимальное, отвечающее требованиям решение. Если
<>
и Sl<>
, то для jєSl определяется аlj>0, допустимое по отношению к Fj(xl) [аlj=0 означает, что j-я целевая функция fj(x) не может принимать значение, отличное от fj (xl)].
Ш а г 3. Решаем задачу
max z
х, z
при условии
Fj(x)єz, jєl ;
Fi(x)>=Fj(x)oj—aj, jєSl; хєХ.
Вызываем исходное решение xl+l. Если xl+1=xl, то задача будет неразрешимой; если xl+1<>xl, то полагаем 1 = 1+1 и возвращаемся к шагу 2.
При этом алгоритм заканчивается.
3.3. Принцип приближения по всем локальным критериям к идеальному решению.
В основу данного подхода положена идея приближения по всем критериям.
Пусть дана задача многокритериального программирования
max{f1(x)=F1},
max{f2(x)=F2}, (3.11)
max{fk(x)=Fk}, xєX,
и заданы граничные условия
(3.12)
(3.13)
x1>=0, x2>=0, …, xn>=0. (3.14)
Среди решений системы (3.11) – (3.14) требуется отыскать такое значение вектора х*(х*1, … , х*n), при котором локальные критерии примут по возможности максимальное (минимальное) значение одновременно.
Рассмотрим каждую отдельную функцию fi(x) и допустим, что для каждого фиксированного i (i=1,m) решена задача максимизации. Пусть соответствующие оптимальные планы характеризуются векторами
xoi(xo1, xo2,…, xon), i=1,m (3.15)
На этих оптимальных планах определим значения критериев соответственно
Foi=(Fi(xo1), Fi(xo2),…, Fi(xon)) (3.16)
Естественно, что векторы (3.15), определяющие векторы точки в пространстве переменных (x1, x2,…, xn)є, будут разными: некоторые из них могут совпадать друг с другом.
Рассмотрим вектор F(х) с компонентами F(x)|Foi из (3.15) и составим квадрат евклидовой нормы
(3.17)
вектора F(x) - Fo, определенного для всех xє.
Заметим, что Fo будет представлять собой единичный вектор в пространстве вектора F(x). Назовем его идеальным значением вектора F(x). Поставленная задача теперь сформулируется так: дана система целевых функций (3.11) и даны условия задачи (3.12) – (3.14). Требуется определить точку xє, в которой функция R(x) достигает минимума.
Таким образом, отыскание векторно-оптимального плана xєв данной задаче сведено к оптимизации выражения (3.17) на решениях системы линейных неравенств (3.12) – (3.14). Поскольку выражение (3.17) представляет собой квадратичную функцию переменных х1, …, хп, то задача отыскания векторно-оптимального плана свелась к задаче выпуклого программирования:
Задана выпуклая функция R(x), определенная на множестве xє. Требуется отыскать точку xє
, обеспечивающую выполнение условия R(x*) = minR(x), xє
.
Таким образом, алгоритм решения задачи (3.11) – (3.14) состоит из двух основных этапов:
этап 1: maxFi(x), i=1, m;
этап 2: min R(x).
3.4. Метод квазиоптимизации локальных критериев (метод последовательных уступок).
В этом случае осуществляется поиск не единственного точного оптимума, а некоторой области решений, близких к оптимальному, – квазиоптимального множества. При этом уровень допустимого отклонения от точного оптимума определяется с учетом точности постановки задачи (например, в зависимости от точности вычисления величины критериев), а также некоторых практических соображений (например, требований точности решения задачи).
Вначале производится качественный анализ относительной важности критериев; на основании такого анализа критерии располагаются и нумеруются в порядке убывания важности, так что главным считается критерий F1, менее важен F2, затем следуют остальные локальные критерии F3, F4,.. ., Fm. Максимизируется первый по важности критерий F1 и определяется его наибольшее значение M1. Затем назначается допустимое снижение (уступка) d1>=0 критерия F1. Определим новую допустимую область X(1), как подобласть X вида
X(1) = Xn{x|F1(x)>=M1-d1} (3.18)
Такой подход позволяет значительно сузить первоначальную допустимую область X, когда переходим к следующему по важности критерию.
После этого находим наибольшее значение М2 второго критерия F2 на множестве X(1) , т. е. при условии, что значение первого критерия должно быть не меньше, чем M1-d1. Снова назначается значение уступки d2>=0, но уже по второму критерию, которое вместе с первым используется при нахождении условного максимума третьего критерия, и т. д. Наконец, максимизируется последний по важности критерий Fm при условии, что значение каждого критерия Fr из m—1 предыдущих должно быть не меньше соответствующей величины Мr - dг; получаемые стратегии считаются оптимальными:
X(i) = X(i-1)n{x|Fi(x)>=Mi-di}
Таким образом, оптимальной считается всякая стратегия, являющаяся решением последней задачи из следующей последовательности задач:
1) найти M1= supF1(x), xєX;
2) найти M2= supF2(x), xєX; (3.19)
…
m) найти Mm= supFm(x), xєX;
Если критерий Fm на множестве стратегий, удовлетворяющих ограничениям задачи m) из (3.19) не достигает своего наибольшего значения Мm, то решением многокритериальной задачи считают максимизирующую последовательность {xk} из последовательности множеств
Xm-1Xm-2
…
X1
X
Практически подобные максимизирующие последовательности имеет смысл рассматривать и для того случая, когда верхняя грань в задаче m достигается, так как для решения экстремальных задач широко применяются итеративные методы.
Алгоритм решения задачи векторной оптимизации включает следующие шаги.
Шаг 1. Пусть х01 — решение задачи (3.19)
max Fl(x), xєX
Шаг 2. Пусть xok - решение задачи
max Fk(x), xєX(k-1)
где Xk определяется из (3.19).
Шаг 3. Если k<m, то устанавливаем k=k+1 и повторяем шаг 2. Если k = m, то хom считаем оптимальным решением.
Алгоритм закончен.
Значения уступок di (i=1,m) последовательно назначаются при изучении взаимосвязи частных критериев.
Вначале решается вопрос о назначении допустимого снижения d1 первого критерия от наибольшего значения М1. Практически для этого задают несколько величин уступок d11 ,d21, d31 ... и путем решения задачи (3.19) определяют соответствующие максимальные значения М2(d11), М2(d21), М2(d31),... второго критерия. Далее рассматривают пару критериев F2 и F3. Вновь назначают пробные значения уступок d12 , d22 ... и, решая задачу (3.21), отыскивают наибольшие значения М3(d12), М3(d22). Полученные данные анализируют, назначают d2, переходят к следующей паре критериев F2 и F3 и т. д. Наконец, в результате анализа взаимного влияния критериев Fm-l и Fm выбирают значение последней уступки dm-1 и отыскивают оптимальные стратегии, решая задачу m из (3.19) (обычно ограничиваются нахождением одной такой стратегии).
Таким образом, хотя формально при использовании метода последовательных уступок достаточно решить лишь от задач (3.19), однако для назначения значения уступок с целью выяснения взаимосвязи частных критериев фактически приходится решать существенно большее число таких задач.
Для решения многокритериальной задачи нужно так ранжировать критерии, чтобы потом удобнее было выбирать значения уступок.
Учитывая вышеизложенное, можно сделать следующий вывод. Метод последовательных уступок целесообразно применять для решения тех многокритериальных задач, в которых все частные критерии естественным образом упорядочены по степени важности, причем каждый критерий настолько существенно более важен, чем последующий, что можно ограничиться учетом только попарной связи критериев и выбирать допустимое снижение очередного критерия с учетом поведения лишь одного следующего критерия.
Особенно удобным является случай, когда уже в результате предварительного анализа многокритериальной задачи выясняется, что можно допустить уступки лишь в пределах «инженерной» точности (5-10% от наибольшей величины критерия).
3.5. Метод свертывания векторного критерия в суперкритерий.
Одним из распространенных методов решения многокритериальных задач является метод сведения многокритериальной задачи к однокритериальной путем свертывания векторного критерия в суперкритерий. При этом каждый критерий умножается на соответствующий ему весовой коэффициент (коэффициент важности).
,
При этом возникают трудности с правильным подбором весовых коэффициентов аi.
Существуют различные способы выбора коэффициентов аi. Одним из них является назначение аi в зависимости от относительной важности критериев. Такой подбор указанных коэффициентов можно выполнять согласно таблице:
Таблица 3.1. Шкала относительной важности.
Интенсивность относительной важности Определение 1 Равная важность сравниваемых требований 3 Умеренное (слабое) превосходство одного над другим 5 Сильное (существенное) превосходство 7 Очевидное превосходство 9 Абсолютное (подавляющее) превосходство 2,4,6,8 Промежуточные решения между двумя соседними оценками
В данной работе рассмотрено более 20 методов подбора весовых коэффициентов. Однако всвязи с большим объемом этой информации ограничимся лишь ссылкой на ресурс, на котором находится указанная статья - http://www.domarev.kiev.ua/nauka/glav_6.htm.
4. Применение генетических алгоритмов для решения задач многокритериальной оптимизации.
Общие сведения о генетических алгоритмах.
Генетические алгоритмы – адаптивные методы поиска, которые часто используются для решения задач функциональной оптимизации. Они основаны на генетических процессах биологических организмов.
Простой ГА случайным образом генерирует начальную популяцию структур. Работа ГА представляет собой итерационный процесс, который продолжается до тех пор, пока не выполнятся заданное число поколений или какой-либо иной критерий остановки. На каждом поколении ГА реализуется отбор пропорционально приспособленности, одноточечный кроссовер и мутация. Сначала, пропорциональный отбор назначает каждой структуре вероятность Ps(i) равную отношению ее приспособленности к суммарной приспособленности популяции. Затем происходит отбор (с замещением) всех n особей для дальнейшей генетической обработки, согласно величине Ps(i). Простейший пропорциональный отбор – рулетка – отбирает особей с помощью n «запусков» рулетки. Колесо рулетки содержит по одному сектору для каждого члена популяции. Размер i-ого сектора пропорционален соответствующей величине Ps(i). При таком отборе члены популяции с более высокой приспособленностью с большей вероятность будут чаще выбираться, чем особи с низкой приспособленностью.
После отбора, n выбранных особей подвергаются кроссоверу (иногда называемому рекомбинацией) с заданной вероятностью Pc. – n строк случайным образом разбиваются на n/2 пары. Для каждой пары с вероятностью Pc может применяться кроссовер. Соответственно с вероятностью 1-Pc кроссовер не происходит и неизмененные особи переходят на стадию мутации. Если кроссовер происходит, полученные потомки заменяют собой родителей и переходят к мутации.
Одноточечный кроссовер работает следующим образом. Сначала, случайным образом выбирается одна из l-1 точек разрыва. (Точка разрыва – участок между соседними битами в строке.) Обе родительские структуры разрываются на два сегмента по этой точке. Затем, соответствующие сегменты различных родителей склеиваются и получаются два генотипа потомков.
После того, как закончится стадия кроссовера, выполняются операторы мутации. В каждой строке, которая подвергается мутации, каждый бит с вероятностью Pm изменяется на противоположный. Популяция, полученная после мутации, записывается поверх старой и этим цикл одного поколения завершается. Последующие поколения обрабатываются таким же образом: отбор, кроссовер и мутация.
Поиск останавливается, когда выполняется условие останова алгоритма. Улучшение состава популяции можно представить следующим образом:
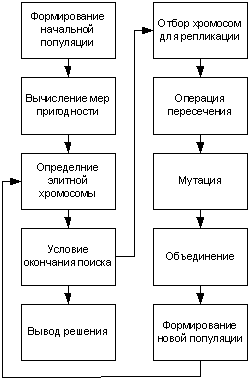
Обобщенная блок-схема генетического алгоритма.
При решении задачи многокритериального программирования с помощью генетических алгоритмов схема решения не отличается от той, которая представлена на рисунке, только вычисление пригодности хромосом и определение элитной хромосомы нужно выполнять для многокритериального случая. При этом самый удобный вариант – свертка локальных критериев в один суперкритерий, то есть получить одну целевую функцию, используя один из методов определения весовых коэффициентов, рассмотренных выше в пункте 3.5.
5. Обощение результатов научного поиска и анализа.
5.1. Существующие проблемы многокритериальной оптимизации.
В ходе проделанной работы был собран материал о существующих методах многокритериальной оптимизации с систематизацией его по разделам. На сегодняшний день существуют такие проблемы многокритериальной оптимизации.
Первая проблема связана с выбором принципа оптимальности, который строго определяет свойства оптимального решения и отвечает на вопрос, в каком смысле оптимальное решение превосходит все остальные допустимые решения. В отличие от задач однокритериальной оптимизации, у которых только один принцип оптимальности f(xо)>=f(x), в данном случае имеется большое количество различных принципов, и каждый принцип может приводить к выбору различных оптимальных решений. Это объясняется тем, что приходится сравнивать векторы эффективности на основе некоторой схемы компромисса.
В математическом отношении эта проблема эквивалентна задаче упорядочения векторных множеств, а выбор принципа оптимальности – выбору отношения порядка.
Вторая проблема связана с нормализацией векторного критерия эффективности F. Она вызвана тем, что очень часто локальные критерии, являющиеся компонентами вектора эффективности, имеют различные масштабы измерения, что и затрудняет их сравнение. Поэтому приходится приводить критерии к единому масштабу измерения, т. е. нормализовать их.
Третья проблема связана с учетом приоритета (или различной степени важности) локальных критериев. Хотя при выборе решения и следует добиваться наивысшего качества по всем критериям, однако степень совершенства по каждому из них, как правило, имеет различную значимость. Поэтому обычно для учета приоритета вводится вектор распределения важности критериев L=(l1, l2,..., ln), с помощью которого корректируется принцип оптимальности или проводится дифференциация масштабов измерения критериев.
К вышесказанному можно добавить также то, что трудности вызывает одновременное наличие в задаче многокритериального программирования качественных и количественных критериев, а именно – перевод из качественных в количественные критерии для дальнейшей оптимизации построенной математической модели. Да и сам правильный подбор весовых коэффициентов иногда сделать не так просто.
5.2. Возможные пути решения проблем многокритериальной оптимизации.
С рассмотренными выше проблемами связаны основные трудности многокритериальной оптимизации, и от того, насколько успешно они будут преодолены, во многом зависят успех и правильность выбора решения. Поэтому здесь непременно должно участвовать ответственное за принятие решения лицо или орган. Таким образом, нужно разрабатывать интерактивные процедуры оптимизации, при которых во время процесса решения задачи производится ввод необходимой информации от ЛПР. Это может быть информация как об относительной важности критериев, так и о том, насколько лучше или хуже остальных изменилось значение конкретного критерия после последнего проделанного шага алгоритма оптимизации.
Возможными путями решения рассмотренных выше проблем многокритериальной оптимизации может быть применение рассмотренных в пункте 2 сверток и способов нормализации.
Также одним из возможных вариантов решения задач многокритериальной оптимизации является использование эволюционных (генетических) алгоритмов. Эта область является перспективной, так как при построении эволюционных методов решения нет четких предписаний, а используются лишь эволюционные принципы построения генетических алгоритмов, то есть построение алгоритма зависит как от выбора операторов мутации, кроссовера, так и от выбора принципа, по которому будут формироваться жизнеспособные хромосомы. Таким образом, можно использовать комбинацию какого-либо из рассмотренных методов многокритериальной оптимизации и генетического алгоритма для решения задачи многокритериальной оптимизации.
5.3. Выбор направления дальнейших исследований и предложения по структуре магистерской работы.
В ходе выполнения данной работы было выбрано дальнейшее направление научной работы. Предполагается применение рассмотренного аппарата многокритериальной оптимизации к конкретному технологическому процессу с оптимизацией его параметров. При этом планируется построение многокритериальной математической модели процесса и решение задачи многокритериального программирования применительно к данной модели. Оптимизацию планируется проводить с использованием программного обеспечения, которое также будет нами разработано в соответствии с примененным методом оптимизации. В качестве алгоритма оптимизации планируется применить комбинацию одного из рассмотренных методов и генетического алгоритма. В качестве кандидатов в применяемые методы могут оказаться методы, основанные на принципе справедливого компромисса либо принципе оптимальности по Парето. При этом на каждом шаге решения значения аргумента планируется получать с помощью эволюционного подхода (генетического алгоритма), то есть путем получения новой популяции хромосом, а отбор жизнеспособных хромосом проводить согласно одного из рассмотренных методов. Также будет учитываться вариант, когда критерии имеют разную важность, то есть все зависит от выбранной модели технологического процесса.
Таким образом, будущая работа заключается в следующем. Вначале будет выбран математический аппарат для решения задачи многокритериальной оптимизации с предварительным обоснованием выбора. Затем будет разработано программное обеспечение для многокритериальной оптимизации конкретного объекта либо процесса в соответствии с выбранным методом. Примерное содержание магистерской работы выглядит следующим образом:
Введение.
1. Анализ существующих методов и моделей многокритериальной оптимизации.
2. Разработка математической модели выбранного технологического объекта.
3. Разработка метода многокритериальной оптимизации для выбранного объекта.
4. Разработка программного обеспечения ля выбранного объекта.
5. Проведение экспериментов по многокритериальной оптимизации и анализ полученных результатов.
6. Обобщение результатов исследований и разработка рекомендаций по их использованию.
Заключение.
Список использованных источников.
1. Г. М. Уланов и др. Методы разработки интегрированных АСУ промышленными предприятиями. М.: Энергоатомиздат – 1983.
2. А. М. Анохин, В. А. Глотов, В.В. Павельев, А.М. Черкашин. Методы определения коэффициентов важности критериев “Автоматика и телемеханика”, №8, 1997, с3-35.
3. Таха, Хэмди А. Введение в исследование операций – М.:Мир,2001, с354-370.
4. Р. Штойер. Многокритериальная оптимизация: теория, вычисления, приложения. М.:Наука, 1982, с14-29, 146-258.
5. Многокритериальная оптимизация. Математические аспекты. М.:Наука, 1989, с116-123.
6. В.В. Подиновский, В.Д. Ногин. Парето-оптимальные решения многокритериальных задач. М.: Наука, 1982, с9-64.
7. В. В. Хоменюк. Элементы теории многокритериальной оптимизации. М.: Наука, 1983, с8-25.
8. Д.И.Батищев, С.А.Исаев, Е.К.Ремер. Эволюционно-генетический подход к решению задач невыпуклой оптимизации. /Межвузовский сборник научных трудов «Оптимизация и моделирование в автоматизированных системах», Воронеж, ВГТУ, 1998г, стр.20-28.
9. Д.И.Батищев, С.А.Исаев. Оптимизация многоэкстремальных функций с помощью генетических алгоритмов. /Межвузовский сборник научных трудов «Высокие технологии в технике, медицине и образовании», Воронеж, ВГТУ, 1997г, стр.4-17.
10. С.А.Исаев. Популярно о генетических алгоритмах. Интернет-ресурс http://bspu.ab.ru./Docs/~saisa/ga/ga-pop.html.
11. С.А.Исаев. Обоснованно о генетических алгоритмах. Интернет-ресурс http://bspu.ab.ru/Docs/~saisa/ga/text/part1.html.
12. С.А.Исаев. Решение многокритериальных задач. Интернет-ресурс http://bspu.ab.ru/Docs/~saisa/ga/idea1.html.
13. Раздел «Математика\Optimization Toolbox». Интернет-ресурс http://www.matlab.ru/optimiz/index.asp.
14. Система СИМОП для автоматизации выбора рациональных решений в комплексах САПР и АСНИ. Интернет-ресурс. http://www.software.unn.ac.ru/mo_evm/research/symop.html
15. Интегрированный пакет многокритериальной оптимизации «МАЛТИ». Интернет-ресурс http://ksu.kst.kz/emf/kafkiber.htm
16. Комплексный инженерный анализ - прочность, динамика, акустика. Интернет-ресурс http://osp.admin.tomsk.ru/ap/1998/02/31.htm
17. Программы семейства COSMOS – универсальный инструмент конечно-элементного анализа.
Интернет-ресурс http://cad.com.ru/7/Info/cosmos_3.html
18. Комплекс СИНТЕЗ-ТФ.
Интернет-ресурс http://www.teleform.ru/index.html.
19. Е.В. Никульчев. Разработка многокритериальных систем управления динамическими объектами. Интернет-ресурс http://do.sssu.ru/ito2001/mater/mgapi.html.
20. И. А. Шварцбуг. Задача оперативного управления контейнерными пунктами. Интернет-ресурс http://www.laboratory.ru/refer/math/rrm001.htm.
| На главную | Полезные ссылки | Библиотека | Индивидуальное задание |
|Отчет о поиске|