В настоящее время считается признанным тот факт, что по причине плохих
метеорологических условий происходит до 40 % летных происшествий. Наиболее
опасными метеорологическим явлением для полетов авиации является низковысотный
сдвиг ветра с большими градиентами составляющих ветра по высоте и дальности,
который обусловлен локальным возмущением состояния атмосферы [10]. Сдвиг ветра
обычно наблюдается в области микропорыва, представляющего собой компактный, но
достаточно интенсивный нисходящий поток холодного воздуха. Обычно микропорыв
распространяется до высоты несколько сот метров и имеет диаметр 5 - 8 км.
Попадая в зону действия микропорыва, экипаж самолета с большим трудом
обеспечивает пилотирование самолетом, неожиданно возникающие возмущения
состояния атмосферы чрезвычайно опасны при посадке. Так они привели к известным
катастрофам [9]: в Международном аэропорту Нового Орлеана 9 июля 1982 г. при
посадке разбился самолет Boing B - 727; в Международном аэропорту Далласа, так
же при посадке , 20 августа 1985 г. потерпел катастрофу самолет Lockheed L -
1011 [6].
В виду большой актуальности проблемы, построения автоматизированных
систем управления полетом, способных предотвращать такого рода катастрофы,
занимались разработчики в разных странах мира. Были предложены различные
алгоритмы управления, основанные на различных физических принципах и
математических концепциях, построенных для различных моделей локального
состояния атмосферы, которые, так или иначе, решали эту задачу.
Практика применения теории оптимальных систем при решении
конкретных задач показала, что оптимальные системы, синтезированные по квадратическому
критерию качества, являются чувствительными к параметрам модели реального объекта и
характеристикам входных воздействий, т.е. являются негрубыми.
Н∞
- теория управления широко применяется в задачах
управления движением. Современный период развития теории управления характеризуется постановкой и решением
задач, учитывающих неточность математической модели объекта управления и действующих
на него внешних возмущений. Задачи синтеза регулятора и оценивания состояния с учетом неопределенности в модели объекта и характеристик входных воздействий являются одними из центральных в современной теории управления.
Идея синтеза робастного управления состоит в том, чтобы одним регулятором обеспечить
устойчивость замкнутой системы не только для номинального (без учета ошибок модели)
объекта, но и для случая "возмущенного" объекта (с учетом неопределенностей модели и
возмущений действующих на объект управления) [1,6].
Получение математической модели продольного движения самолета
В работе рассматривается продольное движение самолета при посадке на
режиме глиссады. На самолет действует внешнее ветровое возмущение ограниченной
мощности. Цель построения системы управления - минимизация влияния внешнего
ветрового возмущения на отклонение контролируемых выходов от заданных значений,
характеризующих глиссаду.
Кинематические и динамические переменные для
уравнения движения центра масс самолета представлены на рис. 1.На рис. 1
введены следующие обозначения: D - сила лобового сопротивления; x, y - оси
системы координат; L - подъемная сила; O - центр масс самолета; V - воздушная
скорость самолета; Ve - скорость самолета относительно земли;
wx, wy - соответственно, горизонтальная и вертикальная
составляющая скорости ветра; α - угол атаки; θ - угол наклона траектории в
воздушной системе координат.
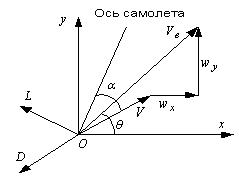
Рисунок 1 - Система координат и переменных самолета
Динамические уравнения движения самолета в вертикальной плоскости с учетом ветровых возмущений,
действующих в проекциях на оси воздушной системы координат, задаются следующей системой
нелинейных дифференциальных уравнений [3]
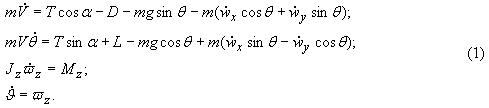
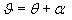 - угол тангажа,
wz - угловая скорость относительно оси z.
- угол тангажа,
wz - угловая скорость относительно оси z.
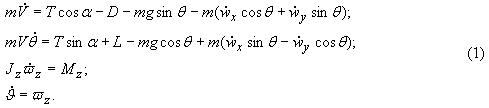
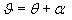 - угол тангажа,
wz - угловая скорость относительно оси z.
- угол тангажа,
wz - угловая скорость относительно оси z.Управление самолетом в продольном канале осуществляется рулем высоты δв и
сектором газа δс.г..
Эти уравнения справедливы в предположении, что направление силы тяги совпадает с осью
самолета, масса самолета постоянна, Земля плоская, ветер стационарный. Вращением
Земли также пренебрегаем.
Приращение угла атаки aw определяется формулой
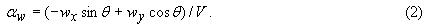

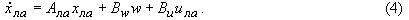
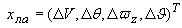 - вектор состояния летательного аппарата,
- вектор состояния летательного аппарата,
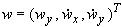 - вектор ветровых возмущений,
- вектор ветровых возмущений,
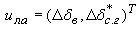 - вектор управления,
где
- вектор управления,
где 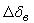 - отклонение руля высоты,
- отклонение руля высоты,
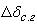 - отклонение силы тяги, выраженное в единицах
измерении сектора газа.
- отклонение силы тяги, выраженное в единицах
измерении сектора газа.
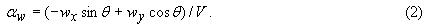

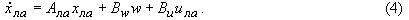
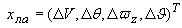 - вектор состояния летательного аппарата,
- вектор состояния летательного аппарата,
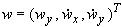 - вектор ветровых возмущений,
- вектор ветровых возмущений,
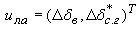 - вектор управления,
где
- вектор управления,
где 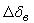 - отклонение руля высоты,
- отклонение руля высоты,
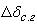 - отклонение силы тяги, выраженное в единицах
измерении сектора газа.
- отклонение силы тяги, выраженное в единицах
измерении сектора газа.Дифференциальное уравнение, описывающее динамику двигателя, задается в виде
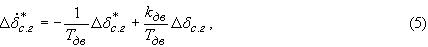
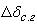 - отклонение
ручки сектора газа от заданного значения.
- отклонение
ручки сектора газа от заданного значения.
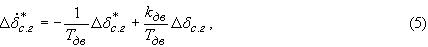
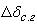 - отклонение
ручки сектора газа от заданного значения.
- отклонение
ручки сектора газа от заданного значения. Формирование отклонения руля высоты 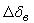 с учетом контура короткопериодического движения осуществляется в следующем виде
с учетом контура короткопериодического движения осуществляется в следующем виде
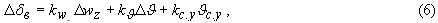
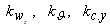 - числовые коэффициенты,
- числовые коэффициенты,
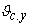 - новое управление,
формируемое регулятором.
- новое управление,
формируемое регулятором.
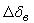 с учетом контура короткопериодического движения осуществляется в следующем виде
с учетом контура короткопериодического движения осуществляется в следующем виде 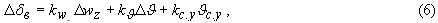
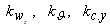 - числовые коэффициенты,
- числовые коэффициенты,
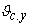 - новое управление,
формируемое регулятором.
- новое управление,
формируемое регулятором.Таким образом, дополнив систему уравнений (4) уравнением (5) с учетом (6) и
линеаризованным уравнением для высоты (3), получаем систему уравнений
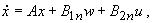 (7)
(7)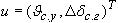 - расширение вектора xла,
- расширение вектора xла,
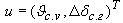 - новый вектор управления, матрицы
A, B1n, B2n получены из матриц Aла, Bw, Bu с учетом (5) и (6).
Уравнение для измеряемого выхода y в пространстве состояния в присутствии шумов измерения ny
записывается в виде
- новый вектор управления, матрицы
A, B1n, B2n получены из матриц Aла, Bw, Bu с учетом (5) и (6).
Уравнение для измеряемого выхода y в пространстве состояния в присутствии шумов измерения ny
записывается в виде

 ,
Iy - единичная матрица размерности (2*2).
,
Iy - единичная матрица размерности (2*2).
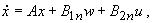 (7)
(7)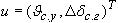 - расширение вектора xла,
- расширение вектора xла,
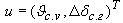 - новый вектор управления, матрицы
A, B1n, B2n получены из матриц Aла, Bw, Bu с учетом (5) и (6).
Уравнение для измеряемого выхода y в пространстве состояния в присутствии шумов измерения ny
записывается в виде
- новый вектор управления, матрицы
A, B1n, B2n получены из матриц Aла, Bw, Bu с учетом (5) и (6).
Уравнение для измеряемого выхода y в пространстве состояния в присутствии шумов измерения ny
записывается в виде
 ,
Iy - единичная матрица размерности (2*2).
,
Iy - единичная матрица размерности (2*2). Математическая модель продольного движения самолета с учетом внешних
ветровых возмущений в пространстве состояния описывается следующей системой уравнений:


Для линейной модели продольного движения самолета с учетом внешних ветровых возмущений в
пространстве состояний (9) вектор управляемых выходов может быть записан в виде

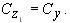

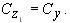
Рассмотрим вектор контролируемых выходов z, определенный следующим образом:


Объединяя (9), (10) и (11), получаем систему уравнений, описывающую управляемую систему:
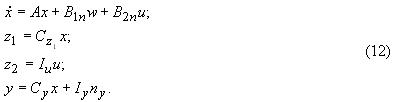
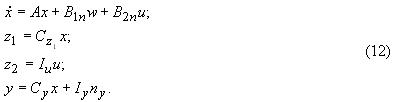
Рассмотрим расширенный вектор входных возмущений


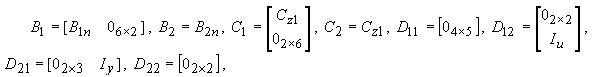


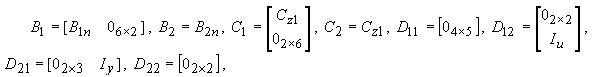
В зависимости от предположений о внешнем возмущении w и о критерии качества получаем разные
оптимальные задачи теории управления.
Синтез ЛКГ регулятора
Произведем синтез фильтра Калмана в условиях действия микропорывов ветра и возмущений, действующих в цепи измерения, необходимо синтезировать наблюдатель, позволяющий оценить переменные состояния объекта управления на основе данных о случайных внешних возмущениях и ошибках измерений. Фильтр Калмана обеспечивает оптимальное решение такой задачи. Для системы вида (12) внешние воздействия в канале возмущений и измерений являются "белым гауссовским шумом" БГШ со следующими характеристиками [5,11]: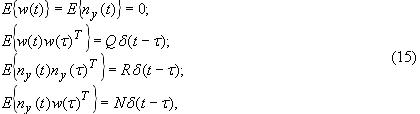
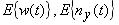 математическое ожидание шумов
математическое ожидание шумов
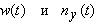 соответственно,
соответственно,
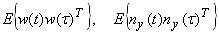 - их ковариационные матрицы,
- их ковариационные матрицы,
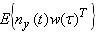 - их корреляционная функция.
- их корреляционная функция.Шум цепи измерения ny(t) поступает в систему через канал
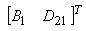 и имеет совместную
корреляционную функцию с шумом состояния w(t)
и имеет совместную
корреляционную функцию с шумом состояния w(t)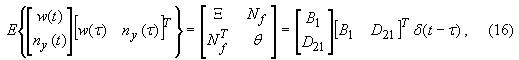

Оптимальным решением является фильтр Калмана, описываемый уравнениями
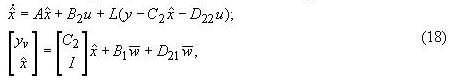
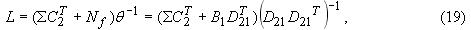
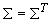 - решение уравнения Риккати вида
- решение уравнения Риккати вида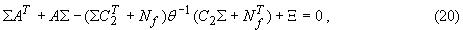
Выберем в качестве критерия оптимальности функционал стоимости вида [4,5,11]
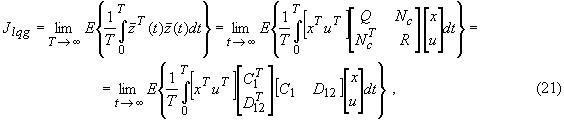
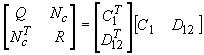 - матрица интенсивности шумов состояния.
- матрица интенсивности шумов состояния.Матрица обратной связи оптимального регулятора равна
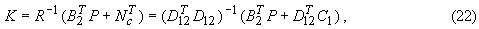
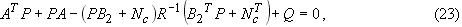

Объединяя объект, фильтр Калмана и оптимальный регулятор, получим ЛКГ регулятор, обеспечивающий фильтрацию шумов измерений входных сигналов объекта [1,5].
Уравнения регулятора в пространстве состояния имеют вид
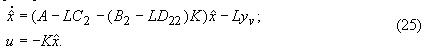

Синтез Н∞-субоптимального регулятора
Нinf - теория управления решает задачу
минимальной чувствительности замкнутой системы для наихудшего случая внешнего возмущения.
Энергия помехи, проходящей на выход, определяется Нinf - нормой матричной передаточной
функции замкнутой системы от внешнего возмущения к контролируемому выходу. Поставленная
задача решена с помощью метода "2-Риккати подхода" [1,7,11].
Пусть удовлетворяются следующие условия:

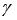 - уровень толерантности, скалярная величина.
- уровень толерантности, скалярная величина.
Синтезированный регулятор имеет структуру фильтра Калмана: 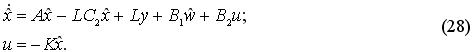
Вычисление матриц обратной связи регулятора и наблюдателя соответственно K и L, а так
же вектора w, который может трактоваться как оценка наиболее неблагоприятного воздействия,
основан на решении матричных квадратичных уравнений Лурье - Риккати.
Синтез регулятора проведен по следующему алгоритму [1]:
- (A,B1,C1) является стабилизируемой и детектируемой;
- (A,B2,C2) является стабилизируемой и детектируемой;
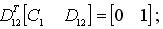
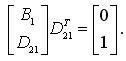

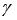 - уровень толерантности, скалярная величина.
- уровень толерантности, скалярная величина.Синтезированный регулятор имеет структуру фильтра Калмана:
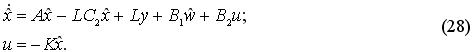
- Задать некоторое значение
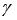 .
. - Найти стабилизирующее решение P≥0 уравнения
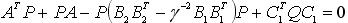 , если решение не существует перейти к пункту 7.
, если решение не существует перейти к пункту 7. - Найти стабилизирующее решение
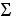 ≥0 уравнения
≥0 уравнения
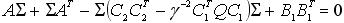 , если решение не существует перейти к пункту 7.
, если решение не существует перейти к пункту 7. - Вычислить матрицу P
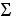 и найти ее максимальное сингулярное число.
и найти ее максимальное сингулярное число.
Если оно больше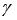 2, то перейти к пункту 7.
2, то перейти к пункту 7. - Вычислить матрицы
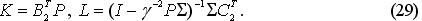
- Определить по формуле

- Зафиксировать, что заданное значение критерия недостижимо, и вернуться к пункту 2,
изменив
 на большую величину.
на большую величину.
Получение математической модели ветрового возмущения
Достаточно полные и наиболее приемлемые
с практической точки зрения модели основаны на теории газовой струи, соударяющейся с плоской
поверхностью, и модели микропорыва ветра в форме вихревого кольца. Генерируемые профили ветра
данной модели позволяют имитировать атмосферные условия, соответствующие некоторым реальным
ситуациям.
Согласно этой модели [8,6] область микропорывов ветра формируется течением вокруг вихревого
кольца, расположенного над плоской поверхностью.
Графики горизонтальной wy и вертикальной составляющих wx профиля ветра относительно центра
вихря в зоне микропорыва ветра на высоте полета 400 м приведены на рис. 2 и 3.
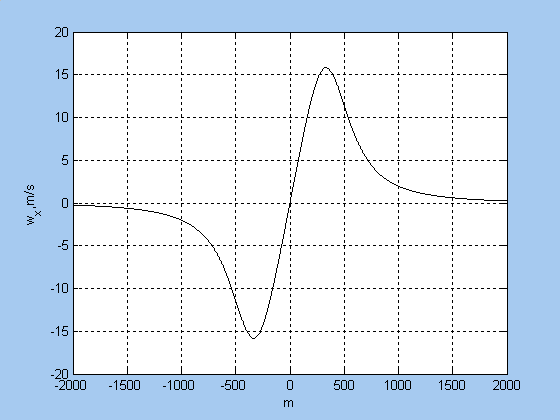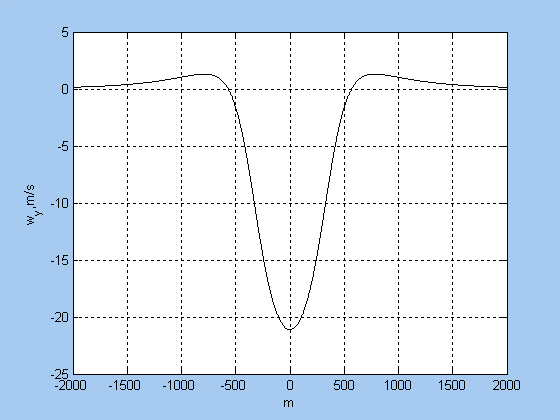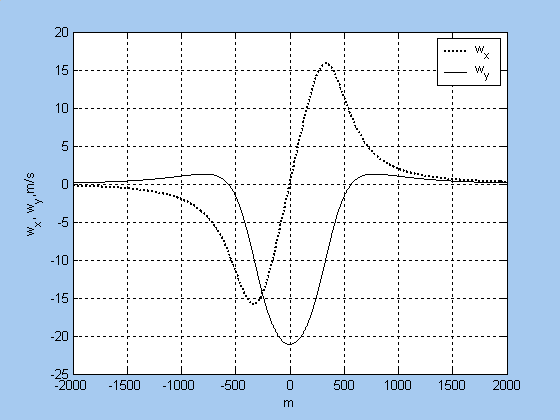
Рисунок 2 - Горизонтальная и вертикальная составляющая профиля ветра
Результаты моделирования
Для проведения автоматизации вычислений и моделирования
составлено законченное
программное обеспечение в пакете прикладных программ MatLab.
Рассматривается движение самолета ТУ - 154 по конкретной траектории глиссады [6].
Эта траектория в координатах высоты и дальности представляет собой прямую линию с заданным углом
наклона траектории 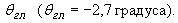 Задача системы управления состоит в том, чтобы при движении по
глиссаде обеспечить постоянную воздушную скорость V =71,375 м/с и заданную высоту при действии
ветровых возмущений (представленных на рис. 2 и 3). Постоянная времени двигателя T0=2.5 c;
kдв=2600 н/град. Коэффициенты равны
Задача системы управления состоит в том, чтобы при движении по
глиссаде обеспечить постоянную воздушную скорость V =71,375 м/с и заданную высоту при действии
ветровых возмущений (представленных на рис. 2 и 3). Постоянная времени двигателя T0=2.5 c;
kдв=2600 н/град. Коэффициенты равны 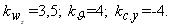
.gif)
.gif)
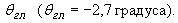 Задача системы управления состоит в том, чтобы при движении по
глиссаде обеспечить постоянную воздушную скорость V =71,375 м/с и заданную высоту при действии
ветровых возмущений (представленных на рис. 2 и 3). Постоянная времени двигателя T0=2.5 c;
kдв=2600 н/град. Коэффициенты равны
Задача системы управления состоит в том, чтобы при движении по
глиссаде обеспечить постоянную воздушную скорость V =71,375 м/с и заданную высоту при действии
ветровых возмущений (представленных на рис. 2 и 3). Постоянная времени двигателя T0=2.5 c;
kдв=2600 н/град. Коэффициенты равны 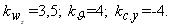
В результате линеаризации нелинейной системы (1) в точке траектории с параметрами
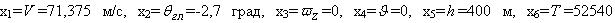 получена
линейная модель объекта управления, соответствующая (12).
получена
линейная модель объекта управления, соответствующая (12).
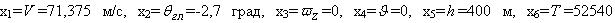 получена
линейная модель объекта управления, соответствующая (12).
получена
линейная модель объекта управления, соответствующая (12).В графических материалах, иллюстрирующих сравнительные характеристики полученных регуляторов,
ЛКГ/Н2 регулятор обозначается LQG, а Н∞ – субоптимальный регулятор – Hinf.
.gif)
Рисунок 4 - График отклонения воздушной скорости V при использовании ЛКГ/Н2 и
Н∞– субоптимального регуляторов
На рис. 4 представлены графики отклонения воздушной скорости V от номинального значения для двух регуляторов.
Максимальное отклонение скорости при использовании ЛКГ регулятора составляет около 14 м/с, а при использовании
Н∞ – субоптимального регулятора – около 10 м/с. Значит по отклонению воздушной
скорости Н∞ – субоптимальный регулятор обеспечивает лучшее качество переходных процессов,
чем ЛКГ/Н2 регулятор.
.gif)
Рисунок 5 - График отклонения высоты h при использовании ЛКГ/Н2 и
Н∞– субоптимального регуляторов
На рис. 5 представлены графики отклонения высоты h от номинального значения для двух регуляторов.
По отклонению высоты Н∞– субоптимальный регулятор так же обеспечивает лучшее качество переходных процессов,
чем ЛКГ/Н2 регулятор. Так максимальное отклонение высоты при использовании ЛКГ регулятора составляет около 40 м,
а при использовании Н∞– субоптимального регулятора – около 20 м, т.е. меньше примерно 2 раза. Эта характеристика
очень важна, потому, что резкая потеря высоты в зоне микропорыва ветра и является основной причиной катастроф при
посадке самолета.
Выводы
Выводы:- Получена линеаризованная математическая модель продольного движения самолета в пространстве состояния с учетом внешних ветровых возмущений.
- Произведен синтез фильтра Калмана в условиях действия микропорывов ветра и возмущения в канале измерения.
- Произведен синтез оптимального регулятора.
- На основе объединения объекта управления, фильтра Калмана и оптимального регулятора получен ЛКГ регулятор, обеспечивающий фильтрацию шумов измерений входных сигналов объекта.
- Произведен синтез Н∞-субоптимального регулятора в условиях действия микропорывов ветра и возмущения в канале измерения.
- Для типового вида ветрового возмущения проведено моделирование замкнутой системы управления с ЛКГ и Н∞-субоптимальным регулятором.
- Решена задача синтеза оптимального регулятора по квадратичному критерию качества, обеспечивающего компромисс между минимально возможным отклонением контролируемых выходов (воздушной скорости и высоты) от номинальных значений и ограничениями по мощности управляющих агрегатов (двигателей и рулей высоты).
- Сделаны выводы о том, что Н∞-субоптимальный регулятор обеспечивает лучшие переходные процессы по отклонениям контролирыемых выходов от номинальных значений.
Список литературы
- Барабанов А.Е., Первозванский А.А. Оптимизация по равномерно частотным показателям (Н∞ - теория)// Автоматика и телемеханика. - 1992. - №6. - С.3-32.
- Бахилина И.М., Степанов С.А. Синтез грубых линейных квадратичных гауссовских регуляторов//Автоматика и телемеханика. - 1998. - №7. - С.96-106.
- Боднер В.А. Системы управления летательными аппаратами. М., Машиностроение, 1973. - 506 с.
- Куропаткин П.В. Оптимальные и адаптивные системы: Учеб. пособие для вузов. - М.: Высш. школа, 1980. – 287 с.
- Медведев В.С., Потемкин В.Г. Control System Toolbox. MATLAB 5 для студентов/ Под общ. ред. к.т.н. В.Г. Потемкина. – М.: ДИАЛОГ – МИФИ, 1999 – 278 с. (Пакеты прикладных программ).
- Методы классической и современной теории автоматического управления: Учебник в 3-х томах. Т.3: Методы современной теории автоматического управления / Под ред. Н.Д. Егупова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. – 748с.
- Позняк А.С., Семенов А.В., Сербряков Г.Г., Федосов Е.А. Новые результаты в H∞-теории управления//Техническая кибернетика.-1991.-№6.-С.10-39.
- Ivan M. A Ring Vortex Downburst Model for Flight Simulation // J. Aircraft, vol. 23. №3. March 1986.
- Miele A., Wang T., Melvin W.W. Gamma guidance scheme for flight in a windshear// J. Guid. Contr. and Dyn., vol. 11. №4, 1998.
- Micle A., Wang T., Melvin W. W. Optimization and acceleration guidance of flight trajectories in a wind shear.//J. Guid. Contr. And Dyn. vol. 10. №4, 1987.
- Robust Control Toolbox User’s Guide, The WathWorks, Inc., 2001.

