Все пакеты прикладных программ (ППП) системы Matlab, входящие в состав группы “Оптимальные и робастные системы управления”, базируются на современных формализованных подходах к математическому моделированию, исследованию и проектированию систем автоматического управления с обратной связью.

Одной из главных особенностей современных формализованных подходов является ориентация на широкий спектр математических оптимизационных задач в конечномерных или бесконечномерных пространствах. Эти задачи представляют собой аналитические инструменты, с помощью которых обеспечивается достижение содержательных практических результатов, ведущих к единой глобальной цели – построению законов управления, удовлетворяющих всей совокупности требований, предъявляемых к проектируемой системе.

В рамках формализованных подходов искомые элементы проектируемой системы, а точнее – их математические модели, формируются как результат решения задач подобного типа. Это существенно отличает современную идеологию от классической теории автоматического управления, где формализованные математические методы применялись, как правило, лишь на этапе анализа какого-либо проектного решения. При этом само такое решение в классике принималось обычно эмпирическим неформальным путем, зачастую – на основе натурного или вычислительного эксперимента.

Тем не менее, следует отметить, что использование современных формализованных подходов не только не исключает привнесение неформального творческого элемента в практику проектирования систем управления, но и всячески его поощряет. Однако базовый акцент делается на формализованных задачах, что позволяет широко применять вычислительную технику на всех этапах проектирования, существенно повысить качество проектных решений, а также освободить проектировщика от тех сложных вопросов, которые на сегодняшний день стали рутинными. Последнее обстоятельство позволяет ему сосредоточиться на проблемах, формализация которых либо совсем невозможна, либо нежелательна по каким-либо причинам.

Основу оптимизационных задач составляет формализация представления о качестве функционирования систем управления. Подобная формализация предполагает, прежде всего, построение некоторой системы количественных характеристик качества функционирования, величины которых зависят от принимаемых проектных решений. Такими характеристиками могут служить различные функционалы, задаваемые в соответствующих метрических пространствах искомых элементов.

Следует отметить, что качество функционирования современных систем управления может быть характеризовано исключительно широким спектром различных функционалов, в зависимости от конкретных задач, объектов управления и условий их эксплуатации. Если пространства искомых элементов нормированы, то в ряде ситуаций их нормы могут использоваться как функционалы качества.

В рамках данной вводной статьи рассматриваются функционалы, на базе которых формируются основные оптимизационные задачи во всех ППП, входящих в состав данной группы.

Один из вариантов современного подхода к формализации понятия качества процесса стабилизации состоит в использовании количественных оценок передаточных матриц замкнутой системы на базе разнообразных матричных норм.

Величины норм передаточных матриц позволяют судить о том, насколько велики выходные сигналы в системе для определенных классов сигналов на ее входе. Если в качестве этих сигналов рассматривать внешние возмущающие воздействия, отклоняющие движение объекта от контролируемого, то качество процесса стабилизации будет тем выше, чем сильнее они подавляются системой. В свою очередь, качество подавления определяется величинами норм передаточной матрицы: чем меньше норма, тем лучше подавляются возмущения. При этом проблема оптимальной стабилизации может быть трактована как проблема такого выбора обратной связи (регулятора), чтобы соответствующая норма передаточной матрицы замкнутой системы была минимальной.

В настоящее время наиболее широко используются методы оптимизации линейных систем управления по нормам пространств Харди и . Осуществим формализацию рассматриваемых понятий и поставим соответствующие задачи о поиске передаточных матриц оптимальных регуляторов.

Рассмотрим блок-схему линейной системы управления, представленную на рис. 1.

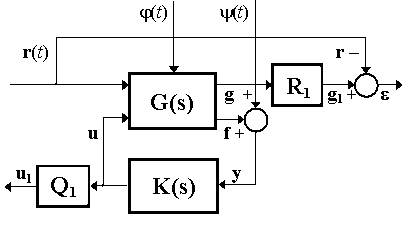
Рис. 1.

Здесь – вектор задающих воздействий, подлежащий отслеживанию с использованием обратной связи. По существу, именно это входное воздействие определяет контролируемое движение замкнутой системы. Векторы и соответственно представляют аддитивные внешние возмущающие воздействия и помехи (шумы) в измерениях. Эти воздействия отклоняют взвешенный выходной вектор объекта от желаемого вектора , определяя ненулевой вектор ошибки слежения , где  – постоянная матрица.

В свою очередь, наличие ненулевой ошибки порождает необходимость во введении корректирующих управляющих воздействий, представленных на схеме внутренним вектором , а также взвешенным выходным вектором регулятора , где  – постоянная матрица. На вход регулятора поступает информация об объекте в виде вектора измерений .

Передаточные матрицы объекта управления и регулятора обозначены на рис. 1 символами и соответственно, векторы и образуют общий вектор выхода объекта управления.

В качестве примера, получим в явном виде выражение для матрицы в случае, когда математическая модель линейной системы исходно представлена уравнениями LTI-объекта в пространстве состояний:

(1)

Здесь – вектор состояния объекта; все прочие указанные ранее векторы имеют следующие размерности: , , , , ; , , , , , , , , ,  – матрицы соответствующих размеров с постоянными компонентами. Записывая систему (1) в изображениях по Лапласу при нулевых начальных условиях, получим

(2)

.

Выполним укрупнение блок-схемы, представленной на рис. 1, вводя в рассмотрение вектор внешних входных воздействий на систему управления, а также вектор ее выходных переменных:

(3)

Результат укрупнения изображен на рис. 2 в виде блок-схемы эквивалентной замкнутой системы с обратной связью с входом и выходом , а также с внутренними переменными и .

Рис. 2.

В свою очередь, полученная блок-схема также может быть укрупнена,  –  результат представлен на рис. 3, где – передаточная матрица замкнутой системы, зависящая от выбора передаточной матрицы регулятора.

Рис. 3.

С учетом (1), а также равенств , и , запишем уравнения LTI-объекта (3) в пространстве состояний:

(4)

Представим в явном виде выражения для передаточных матриц и разомкнутой и замкнутой систем соответственно для LTI-объекта с уравнениями состояния (4), записанными в изображениях по Лапласу при нулевых начальных условиях:

(5)

В соответствии с (4), передаточная матрица разомкнутой системы имеет вид

(6)

где , , – единичные матрицы размеров , и соответственно.

Для формирования передаточной матрицы замкнутой системы, с учетом введенных выше обозначений (3), представим уравнение LTI-объекта (5) в следующем виде

, (7)

предварительно выполнив разбиение найденной передаточной матрицы (6) разомкнутой системы на соответствующие блоки.

Далее, к уравнениям объекта управления (7) следует добавить уравнение регулятора

, (8)

и исключить из уравнений замкнутой системы (7), (8) переменные и . С этой целью подставим (8) во второе уравнение системы (7), получая при этом , откуда, с учетом (8), имеем

. (9)

После подстановки формулы (9) в первое уравнение системы (7), получим

, (10)

где – единичная матрица.

Итак, уравнения замкнутой системы в изображениях по Лапласу при нулевых начальных условиях представлены в виде

(11)

где передаточная матрица замкнутой системы имеет вид

.

Замечание: Приведенное представление передаточной матрицы замкнутой системы (7), (8) в литературе по современным методам оптимального управления получило наименование нижнего дробно-линейного преобразования (LFT) матрицы матрицей .

Найденная матрица может трактоваться как обобщенный "матричный коэффициент усиления" между внешним входным возмущением и обобщенным выходным вектором замкнутой системы.

В соответствии с изложенным выше, целью управления является уменьшение ошибки слежения за задающим воздействием . Естественно, что это желательно делать с минимально возможным управляющим сигналом в целях экономии энергетических ресурсов управления. Очевидно, что чем "меньше" будет матричный коэффициент в замкнутой системе (11), т.е. чем сильнее будет подавлено внешнее воздействие , тем лучше будет качество слежения.

В связи с этим целесообразно сформулировать задачу о наилучшем подавлении внешних возмущений, влияющих на замкнутую систему, путем уменьшения матричного коэффициента за счет выбора передаточной матрицы регулятора .

Для формализации задачи, прежде всего, следует формализовать требование "малости" передаточной матрицы замкнутой системы. Очевидно, что это можно сделать с использованием понятия некоторой матричной нормы . Тогда на формальном уровне обобщенная задача подавления внешних возмущений принимает вид

(12)

где  – множество передаточных матриц с дробно-рациональными компонентами, для которых характеристический полином замкнутой системы (11) является гурвицевым.

Выбор конкретной нормы в (12) порождает различные классы современных задач оптимального синтеза стабилизирующих управлений, среди которых в настоящее время наиболее популярными являются следующие:

•   задачи о минимизации нормы (типичный представитель – задача LQG-оптимального синтеза);
•   задачи о минимизации нормы (задача -оптимального синтеза);
•   задачи о минимизации указанных выше норм для "взвешенных" передаточных матриц , где – заданная весовая матричная функция (например, задачи среднеквадратичного оптимального синтеза и синтеза гарантирующих регуляторов соответственно).

В дальнейшем везде будем считать, что все корни характеристического полинома замкнутой линейной системы с математической моделью вида (11) расположены в открытой левой полуплоскости. Кроме того, будем считать, что для всех рассматриваемых далее передаточных матриц выражение является строго правильной рациональной дробью. Тогда указанные выше нормы вводятся следующими соотношениями:

а) норма :

(13)

в частности, для SISO-задачи (со скалярными входом и выходом ) получим

(14)

б) норма :

(15)

где  – максимальное сингулярное число матрицы (корень квадратный из максимального собственного значения эрмитовой матрицы ), в частности, для SISO-задачи имеем

(16)

в) взвешенная норма :

т.е.

(17)

где ;

в частности, для SISO-задачи –

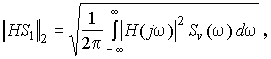(18)

где ;

г) взвешенная норма :

(19)

где  – максимальное сингулярное число матрицы .

Заметим, что к поставленной задаче наилучшего подавления внешних возмущений на входе можно подойти и с другой стороны, вводя понятие качества процесса управления не косвенно через норму передаточной матрицы замкнутой системы, а непосредственно через характеристики выходного векторного сигнала , который по существу идеи должен быть достаточно малым в определенном смысле. Сопоставление двух подходов позволит придать физический смысл приведенным выше вариантам матричных норм.

Рассмотрим устойчивую линейную систему, представленную математической моделью вида

, . (20)

Для формализации понятия малости векторного выходного сигнала замкнутой системы, введем в рассмотрение скалярную переменную

(21)

которую будем в дальнейшем рассматривать в качестве некоторого обобщенного выходного процесса, характеризующего динамику замкнутой системы в целом. В свою очередь, качество этого процесса будем оценивать одной из норм функции , определяемых следующими соотношениями:

а) норма пространства :

(22)

б) норма пространства :

(23)

в) среднеквадратичная норма:

(24)

где  – знак математического ожидания, – дисперсия.

Будем считать, что свойства входных воздействий и передаточных матриц замкнутой системы таковы, что величины (22) – (24) конечны. Очевидно, что нормы и целесообразно использовать в тех случаях, когда входные воздействия являются детерминированными функциями времени, а норму  –  когда в качестве входных воздействий выступают стационарные центрированные случайные процессы.

Будем говорить, что векторный выходной сигнал является в определенном смысле малым, если соответствующая норма из совокупности (22) – (24) достаточно мала.

При этом для управляемой линейной системы вида (11), аналогично задаче (12), может быть поставлена задача о наилучшем подавлении входных возмущений в смысле минимизации той или иной нормы функции :

(25)

Задачи типа (25), в отличие от задач (12), рассматриваются при заданных характеристиках вектора входных воздействий : в детерминированном случае должны быть известны его компоненты, как функции времени на интервале (или изображения по Лапласу от этих функций), а в стохастическом случае – матрица спектральных плотностей стационарного центрированного случайного процесса .

Очевидно, что задачи типа (12) связаны с задачами типа (25). Рассмотрим эту связь вначале для детерминированной, а затем для стохастической ситуации.

а)  Пусть на вход системы поступает векторный детерминированный сигнал с изображением по Лапласу . При этом для изображения по Лапласу выходного сигнала при нулевых начальных условиях по соответствующему вектору состояния справедливо равенство

(26)

Отметим, что, в соответствии с формулой Парсеваля:

(27)

При этом, согласно (21), (22), имеем

(28)

или, с учетом (26),

(29)

Сопоставляя (29) с (17), убеждаемся в том, что = при условии, что . Иными словами, норма обобщенного выходного сигнала в пространстве совпадает с взвешенной нормой передаточной матрицы линейной системы в пространстве при условии, что весовая матрица определяется изображением по Лапласу входного сигнала.

б)  Пусть на вход системы поступает векторный стационарный центрированный случайный процесс с заданной матрицей спектральных плотностей .

При этом из теории случайных векторных процессов следует, что

(30)

где  – матрица спектральных плотностей выходного вектора . Как известно, при прохождении сигнала через линейную систему с передаточной матрицей его матрица спектральных плотностей преобразуется по формуле

(31)

С учетом (31), формула (30) примет вид

откуда с учетом (21), (24) имеем

Из последней формулы следует, что среднеквадратичная норма обобщенного выходного сигнала совпадает с взвешенной нормой передаточной матрицы замкнутой системы в пространстве при условии, что весовая матрица удовлетворяет тождеству , т.е. представляет собой результат факторизации матрицы спектральных плотностей входного сигнала . Иными словами, при указанных условиях справедливо равенство

. (32)

В силу проведенных рассуждений справедливо следующее утверждение:

Теорема 1. -норма передаточной матрицы замкнутой системы совпадает со среднеквадратичной нормой обобщенного выходного сигнала , порожденного l-мерным белым шумом на входе, имеющим единичную матрицу спектральных плотностей.

Доказательство. В соответствии с условием теоремы, непосредственно из формулы (32) имеем

, (33)

что и требовалось доказать.

Наряду с отмеченным свойством характеристик замкнутой системы, имеет место еще одна принципиально важная связь между рассматриваемыми нормами, которая может быть представлена следующим утверждением:

Теорема 2. Для любых пар входных и выходных сигналов замкнутой системы с математической моделью (11) выполняется неравенство вида

. (34)

Доказательство. Предварительно рассмотрим эрмитову матрицу размера . Для каждой фиксированной частоты определим ее собственные числа (отметим, что они все действительные и неотрицательные), обозначая их символами , где . Каждому собственному числу поставим в соответствие собственный вектор матрицы и построим вспомогательные матрицы и следующего вида

,

.

При этом будем считать, что матрица собственных векторов нормирована, т.е. выполняются равенства

, (35)

где символ “*” обозначает эрмитово сопряжение.

По определению собственных чисел и собственных значений, имеем

или ,

откуда следует . Отсюда, с учетом (35), получим

. (36)

Теперь обратимся к формулам (21), (22), (26), (27) для определения L₂ – нормы выходного вектора системы:

.

Отсюда, вводя обозначение

, (37)

непосредственно имеем

. (38)

Заметим, что согласно (37) и (35), справедливы равенства

. (39)

Обозначим диагональные элементы матрицы символами , где . Тогда имеем равенство , которое подставим в формулу (38):

, (40)

где через обозначено максимальное собственное значение матрицы или, что то же самое, квадрат максимального сингулярного числа матрицы . Продолжая преобразование неравенства в (40), получим далее

что, с учетом формул (15) и (27), приводит к неравенству (34), т.е. полностью доказывает теорему. ■

Замечание: Можно показать, что для любого сколь угодно малого числа найдется такой входной сигнал , что будет выполнено неравенство , где – соответствующий выходной сигнал системы (11).

Заметим, что соотношение (34) позволяет трактовать норму как -коэффициент усиления (или RMS-коэффициент усиления – random mean square) устойчивой линейной системы (20).

На базе теоремы 2 можно наглядно интерпретировать понятие нормы в рамках частной ситуации, когда на вход устойчивой линейной системы (20) поступает векторный сигнал , компонентами которого служат гармонические колебания одинаковой частоты с различными амплитудами и фазами:

. (41)

В соответствии с известным свойством линейных систем, выходной вектор в установившемся режиме движения будет иметь аналогичные гармонические компоненты, т.е.

.

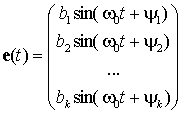Пусть при этом вектор амплитуд входного сигнала удовлетворяет условию (евклидова норма). Тогда, на основании неравенства (34), для вектора амплитуд выходного сигнала справедливо соотношение

. (42)

Более того, можно показать, что в данном случае для любого и для любых фаз входного сигнала выполняется равенство .

Приведенная интерпретация допускает и несколько иную трактовку. Пусть для любой частоты на вектор амплитуд входного сигнала наложено ограничение . Поставим целью выявить условие, которому должны удовлетворять динамические свойства системы (20), чтобы для любой частоты вектор амплитуд выходного сигнала был аналогичным образом ограничен, т.е. . Это достаточное условие с очевидностью вытекает из (42) и имеет вид

. (43)

Подобным образом можно использовать и понятие взвешенной -нормы. Предварительно заметим, что при выводе неравенства (43) совершенно не учитываются частотные особенности входного сигнала и требования к частотным свойствам выходного сигнала . Однако в практических задачах их учет бывает крайне желателен при синтезе замкнутой системы.

Учет спектральных особенностей входного сигнала можно обеспечить, считая, что компоненты вектора входных амплитуд удовлетворяют неравенствам

, , , (44)

где – заданные рациональные дроби с гурвицевыми знаменателями.

Из (44) следует, что . Полученное неравенство заменим более жестким требованием

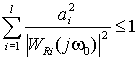(45)

и будем считать, что оно справедливо для входного сигнала . Тогда для вспомогательного сигнала , удовлетворяющего уравнению

, (46)

где , выполняется условие

. (47)

Теперь осуществим учет требований к частотным свойствам выходного сигнала системы (20). Это можно сделать, полагая, что компоненты вектора выходных амплитуд должны удовлетворять неравенствам

, , , (48)

где – заданные рациональные дроби с гурвицевыми знаменателями.

Из (48) следует, что , причем это неравенство, аналогично входу, также заменим более сильным требованием

. (49)

Тогда для вспомогательного сигнала , удовлетворяющего уравнению

, (50)

где , должно выполняться требование

. (51)

Учитывая уравнения (46) и (50), можно построить блок-схему прохождения указанных выше сигналов, которая изображена на рис. 4.

Рис. 4.

Очевидно, что вспомогательные сигналы и связаны между собой уравнением

. (52)

Для устойчивой линейной системы с моделью (52), где входной вектор удовлетворяет условию (47), требуется, чтобы выходной вектор удовлетворял неравенству (51). Но ранее было показано, что, согласно (43) и (52), для этого достаточно, чтобы

. (53)

Таким образом, для выполнения требований (48) при выполняющихся по предположению условиях (44) достаточно, чтобы имело место неравенство (53), аналогичное неравенству (43). В этом и состоит интерпретация взвешенной нормы пространства с весами и .

В руководстве пользователя пакета “-Tools” приводится также предельно упрощенный вариант интерпретации указанной взвешенной нормы, который в общем случае не справедлив, однако дает вполне ясное представление о физическом смысле данной характеристики. Суть этой трактовки состоит в том, что условие выполняется тогда и только тогда, когда для любых входных сигналов вида (41) с любой частотой и любыми амплитудами, удовлетворяющими неравенствам (44), амплитуды соответствующих выходных сигналов удовлетворяют неравенствам (48).