| |
Имитационный метод определения нагрузки
промышленных электрических сетей
Беляев Д.В., руководитель: к.т.н., доцент Погребняк Н.Н.
В основе проекта электроснабжения промышленных предприятий лежит расчет электрических нагрузок, по которым осуществляется выбор необходимых сечений проводников, коммутационной и защитной аппаратуры, позволяющий спроектировать сеть электроснабжения и оценить электромагнитную совместимость (ЭМС) электроприемников (ЭП). Промышленные предприятия потребляют около двух третей вырабатываемой электроэнергии, поэтому требования к точности расчетов нагрузок достаточно велики. Их результат сказывается на технико-экономических показателях системы (завышение электрических нагрузок ведет к увеличению капиталовложений, занижение может привести к возникновению аварийной ситуации, дополнительным потерям электроэнергии, ущербу из-за электромагнитной несовместимости ЭП), а в целом на эффективность работы предприятия, его экономические показатели и конкурентоспособность.
Многочисленные исследования показали, что расчетные нагрузки завышаются, это привело к существенному завышению капиталовложений в сети электроснабжения. Ущерб же от нарушения ЭМС составляет порядка сотен миллионов гривен в год. Отсюда возникает необходимость исследований в области электрических нагрузок и, в первую очередь, необходимость совершенствования действующих Указаний по их расчету.
Эмпирические методы расчета начали разрабатываться еще в тридцатые годы (Копытов Н.В., Тихонов В.П. и др.). За рубежом интерес к методам расчета электрических нагрузок появился после начала Второй мировой войны (Adams C.A., Fetcher J.R., Johnson A.C., Adler H.A., Miller K.W., Boice W.K.). Однако существенные результаты были достигнуты в шестидесятые годы за счет использования вероятностных методов анализа случайных величин (Каялов Г.М., Гнеденко Б.В., Волобринский С.Д., Мукосеев Ю.Л. и др. [3, 4] ). Окончательно методологический подход сформировался в рамках концепции случайных процессов. При этом сложность и нелинейность задач электроснабжения потребовали использование методов имитации случайных процессов.
С 1992 г. и по настоящее время при проектировании систем электроснабжения (СЭС) расчет электрических нагрузок выполняют по действующим Указаниям [2], в основу которых положен модифицированный статистический метод (МСМ) [1]. Использование его взамен метода упорядоченных диаграмм позволило избежать значительного завышения расчетных нагрузок за счет коррекции среднего значения групповой нагрузки. Но в качестве расчетной нагрузки, в методе, принимается расчетный максимум кумулятивного процесса – осредненного на 30-ти минутном интервале группового графика нагрузки, что не отвечает физике процесса нагрева проводника. Положению статистического метода о нормальном законе распределения кумулятивного графика противоречит допущение о наличии корреляционной связи между его средним значением и стандартом. Расчетные выражения МСМ (13) и (14) из [1] дают бесконечное значение коэффициента 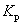 расчетной нагрузки при эффективном числе ЭП расчетной нагрузки при эффективном числе ЭП 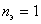 . По этой причине кривые для определения . По этой причине кривые для определения 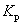 в [2], показанные на рис. 1, имеют необъяснимые перегибы, хотя с ростом эффективного числа ЭП значение коэффициента расчетной нагрузки должно монотонно уменьшаться. в [2], показанные на рис. 1, имеют необъяснимые перегибы, хотя с ростом эффективного числа ЭП значение коэффициента расчетной нагрузки должно монотонно уменьшаться.
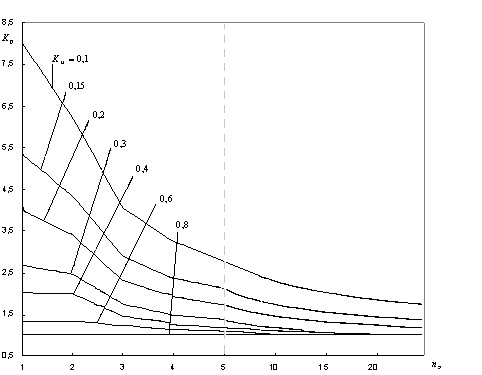
Рисунок 1 – Зависимости коэффициента расчетной нагрузки 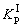 от эффективного числа ЭП от эффективного числа ЭП
Для решения задач с повышенной точностью предлагаем использовать разработанный на кафедре ЭПГ Донецкого национального технического университета, имитационный метод расчета электрических нагрузок.
Целью расчета метода является определение закона распределения температуры 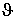 перегрева проводника, а по нему - расчетной нагрузки. Для решения задачи о нагреве проводника случайной нагрузкой была принята предложенная профессором Г.М. Каяловым [5, стр.7], [3, стр. 32] и применяемая в теории электрических нагрузок [7, стр. 34] простая тепловая модель проводника. В основу этой модели положены следующие допущения: перегрева проводника, а по нему - расчетной нагрузки. Для решения задачи о нагреве проводника случайной нагрузкой была принята предложенная профессором Г.М. Каяловым [5, стр.7], [3, стр. 32] и применяемая в теории электрических нагрузок [7, стр. 34] простая тепловая модель проводника. В основу этой модели положены следующие допущения:
- температура в каждой отдельной точке поперечного сечения проводника практически не изменяется по его длине;
- проводник считается однородным телом с нулевым внутренним тепловым сопротивлением, так как основным фактором неоднородности строения проводника является изоляция его жил, слой которой для напряжения до 6 кВ относительно невелик.
При принятых допущениях условие теплового баланса для трехжильного кабеля, открыто проложенного внутри помещения, при токе нагрузки 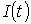 в амперах имеет вид [5, стр.7], [3, стр. 32] в амперах имеет вид [5, стр.7], [3, стр. 32]
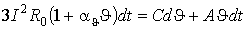 , (1) , (1)
где 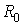 - активное сопротивление жилы проводника при температуре 20°С , Ом; - активное сопротивление жилы проводника при температуре 20°С , Ом;
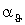 - температурный коэффициент сопротивления, 1/°С; - температурный коэффициент сопротивления, 1/°С;
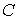 - теплоемкость проводника, Дж/°С; - теплоемкость проводника, Дж/°С;
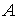 - коэффициент теплоотдачи, учитывающий суммарную отдачу тепла в окружающую среду за счет теплопроводности, конвекции и лучеиспускания, Вт/°С . - коэффициент теплоотдачи, учитывающий суммарную отдачу тепла в окружающую среду за счет теплопроводности, конвекции и лучеиспускания, Вт/°С .
Из (1) получено уравнение для перегрева проводника относительно окружающей среды
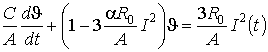 . (2) . (2)
В [5, стр.8], [3, стр.33] показано, что рост значения
коэффициента теплоотдачи практически компенсирует одновременное возрастание сопротивления 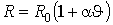 .
Поэтому в (2) с допустимой для .
Поэтому в (2) с допустимой для  погрешностью
принято погрешностью
принято 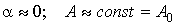 . Тогда уравнение (2) примет вид . Тогда уравнение (2) примет вид
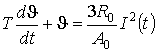 , (3) , (3)
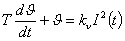 , (4) , (4)
где 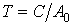 - постоянная времени нагрева проводника, - постоянная времени нагрева проводника, 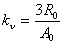 ; ;
Таким образом, к перечисленным допущениям добавляются еще два: постоянная времени нагрева и активное сопротивление проводника не зависят от температуры нагрева. В установившемся режиме при незначительных колебаниях температуры это упрощение не приводит к большой погрешности. Для удобства выполнения расчетов применим подстановку 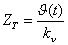 , в результате которой уравнение (4) примет вид , в результате которой уравнение (4) примет вид
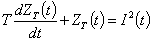 , (5) , (5)
или, применительно к групповому графику 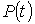 активной нагрузки, активной нагрузки,
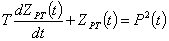 . (6) . (6)
Величина 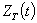 ( ( 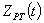 ) названа греющей дозой, она пропорциональна температуре перегрева проводника и имеет размерность квадрата нагрузки. ) названа греющей дозой, она пропорциональна температуре перегрева проводника и имеет размерность квадрата нагрузки.
Исходными для определения расчетных нагрузок являются процессы изменения электрических нагрузок. Профессор Г.М. Каялов в методе вероятностного моделирования для изучения графиков нагрузок впервые применил теорию случайных функций и импульсных потоков. Метод стал теоретической базой для проведения дальнейших исследований. Моделирование групповых графиков - результат суммирования индивидуальных, таким образом задача сводилась к созданию алгоритма моделирования индивидуального графика.
Строгая периодичность последнего формируется при работе электроприемника с максимальной нагрузкой. Изучение этого графика, несмотря на его маловероятность на практике, имеет теоретическое значение, так как он соответствует предельному режиму. Сложности в определении диапазона изменения, характеристик и закона распределения температуры нагрева проводника для периодического импульсного графика уже решены, модель случайного индивидуального графика нагрузки должна быть задана:
- номинальной активной нагрузкой 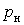 , кВт; , кВт;
- коэффициентом использования
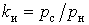 , (7) , (7)
где 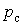 - средняя активная нагрузка, кВт; - средняя активная нагрузка, кВт;
- коэффициентом загрузки
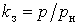 , (8) , (8)
где 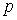 - средняя мощность, потребляемая ЭП во время включения, кВт; - средняя мощность, потребляемая ЭП во время включения, кВт;
- коэффициентом реактивной мощности 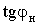 ; ;
- видом и значениями параметров корреляционной функции (КФ) или величиной среднего времени цикла 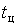 . .
Коэффициенты включения 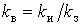 и отключения и отключения 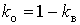 равны соответственно вероятностям включенного и отключенного состояний ЭП. равны соответственно вероятностям включенного и отключенного состояний ЭП.
В работе приняли индивидуальный график активной электрической нагрузки двухступенчатым: он состоит из импульса величиной 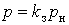 продолжительностью продолжительностью 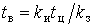 и нулевой паузы и нулевой паузы 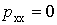 длительностью длительностью 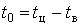 . .
В реальных условиях ЭП работают с некоторой, но не строгой периодичностью. Поэтому КФ индивидуальной нагрузки может быть аппроксимирована выражением
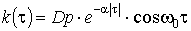 , (9) , (9)
где 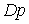 - дисперсия индивидуального графика нагрузки; - дисперсия индивидуального графика нагрузки;
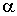 - параметр
КФ, обратный времени корреляции, с-1 - параметр
КФ, обратный времени корреляции, с-1
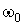 - частота периодической составляющей, с-1. - частота периодической составляющей, с-1.
По опубликованные нормированные КФ индивидуальных графиков активной мощности 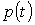 , полученным экспериментально в действующих системах электроснабжения, видно, что для индивидуальных графиков нагрузок, в основном, характерна экспоненциально-косинусоидальная КФ. , полученным экспериментально в действующих системах электроснабжения, видно, что для индивидуальных графиков нагрузок, в основном, характерна экспоненциально-косинусоидальная КФ.
Параметры КФ могут быть определены как экспериментально, так и из технологических расчетов. В последнем случае индивидуальную нагрузку представляют в виде импульсного процесса, дисперсию и параметры КФ которого можно определить по формулам:
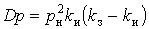 , , 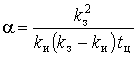 , , 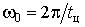 . (10) . (10)
Переходя к модели группового графика, отметим, что несмотря на нестационарность суточного графика нагрузки, на нем можно выделить участки, на которых групповой график является стационарным эргодическим случайным процессом.
Достоинством модели является то, что характеристики группового графика нагрузки определяются по известным характеристикам индивидуальных графиков согласно формулам для числовых характеристик суммы случайных функций.
Для группы массовых ЭП присущая индивидуальным графикам нагрузки периодичность в групповом графике практически не проявляется, поэтому в теории электрических нагрузок в частности, в методах вероятностного моделирования и инерционном, принято, что КФ группового графика имеет вид
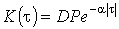 , (11) , (11)
где 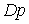 -дисперсия группового графика нагрузки. Принятая модель групповой нагрузки с экспоненциальной КФ обеспечивает некоторый запас при определении расчетных нагрузок. -дисперсия группового графика нагрузки. Принятая модель групповой нагрузки с экспоненциальной КФ обеспечивает некоторый запас при определении расчетных нагрузок.
Коэффициент формы, равный отношению эффективной 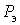 нагрузки к средней нагрузки к средней 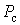 : : 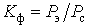 , характеризует неравномерность графика нагрузки. , характеризует неравномерность графика нагрузки.
Рассмотрим закон распределения ординат группового графика. Представив индивидуальную нагрузку в виде импульсного процесса, функцию распределения групповой нагрузки можно рассчитать, используя теорему о повторении опытов. Количество одновременно работающих ЭП и групповая нагрузка при одинаковых величинах импульсов всех ЭП подчиняется биномиальному закону распределения. Обычно значения импульсов отдельных ЭП различны. В этом случае закон распределения нагрузки условно будем называть “комбинаторным”.
Академик Б.В. Гнеденко теоретически доказал, что нормальный закон распределения нагрузки можно считать справедливым для магистралей, питающих более 6 ЭП. Таким образом, в работе примем, что групповая нагрузка распределена нормально, а в случае небольшого количества ЭП и при наличии выпадающих из ряда по мощности или режиму работы ЭП закон вероятностного распределения нагрузки будем называть комбинаторным и рассчитывать по теореме о повторении опытов.
Алгоритм имитационного метода определения расчетной нагрузки включает следующие этапы:
- имитация ансамбля реализаций группового графика тока нагрузки 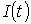 или активной мощности или активной мощности 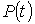 ; ;
- расчет ансамбля реализаций греющей дозы 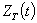 ( ( 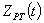 ) согласно интегралу Дюамеля ) согласно интегралу Дюамеля
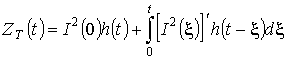 , (12) , (12)
где 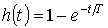 – переходная функция инерционного звена. – переходная функция инерционного звена.
- расчет статистической функции распределения греющей дозы по сечению полученного ансамбля 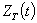 ( ( 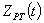 ), взятому после затухания переходного процесса нагрева проводника в момент времени ), взятому после затухания переходного процесса нагрева проводника в момент времени 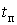 ; ;
- определение расчетного максимального значения греющей дозы 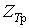 или или 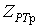 с заданной граничной вероятностью с заданной граничной вероятностью 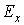 в соответствии с принципом практической уверенности по статистической функции распределения греющей дозы в соответствии с принципом практической уверенности по статистической функции распределения греющей дозы 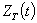 ( ( 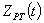 ) )
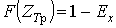 или или 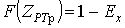 ; (13) ; (13)
- определение расчетной нагрузки по току 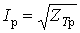 или по активной мощности или по активной мощности 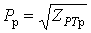 . .
Имитационный метод был применен для определения статистических закономерностей [9], на основании которых разработан инженерный метод греющих доз (ГД) [13]. Этот метод имеет более высокую точность, чем МСМ. На его основе составлен проект Указаний по расчету электрических нагрузок промышленных предприятий, принятый ОАО «Киевпромэлектропроект» для апробации, и широко используется в научно-исследовательской работе студентов.
Недостатком имитационного метода является упрощение в реализации: реактивная нагрузка рассчитывается с помощью инженерного метода, что не отвечает идее имитационного метода и ведет к снижению точности расчетов. Поэтому было предложен усовершенствованный имитационный метод, температура перегрева проводника в соответствии с которым определяется по полной нагрузке. Для определения расчетной нагрузки усовершенствованным имитационным методом имитируется ансамбль реализаций группового графика полной нагрузки. Количество реализаций ансамбля, необходимое для получения достоверного значения расчетной нагрузки определяется статистическими методами и составляет порядка 5-10 тысяч.
Длительность каждой реализации определяется временем окончания переходного процесса нагрева проводника с постоянной времени нагрева Т и принимается равной 5Т.
Для получения одной реализации группового графика нагрузки моделируются индивидуальные графики активной и реактивной нагрузок каждого электроприемника. Групповые графики активной и реактивной нагрузок получаются путем суммирования соответствующих индивидуальных графиков. По групповым графикам активной и реактивной нагрузок определяется групповой график полной нагрузки.
Используя интеграл Дюамеля, по ансамблю реализаций группового графика полной нагрузки рассчитывается ансамбль реализаций греющей дозы.
Для определения расчетного значения греющей дозы по сечению ансамбля греющих доз, взятому после завершения переходного процесса нагрева проводника рассчитывается статистическая функция распределения греющей дозы.
По статистической функции распределения греющей дозы определяем ее расчетное максимальное значение (значение, которое может быть превышено с вероятностью 0,05). Расчетная полная нагрузка равна квадратному корню из греющей дозы.
Графически, работу программы можно проиллюстрировать следующим образом (рисунок 1.1):

Рисунок 1.1- Метод расчета нагрузки уточненным имитационным методом
Составлена программа позволяющая рассчитать нагрузку каждого участка электрической сети любой конфигурации уточненным имитационным методом. Также программа может применяться для моделирования реализаций групповых графиков электрических нагрузок, при оценке точности существующих и разрабатываемых инженерных методов расчета электрических нагрузок.
Недостатком метода является большая продолжительность расчета, поскольку необходимая точность достигается имитацией большого количества реализаций графиков электрической нагрузки.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Жохов Б.Д. Анализ причин завышения расчетных нагрузок и возможной их коррекции // Промышленная энергетика. - 1989. - №7. - С.17-21
2. Руководящий технический материал. Указания по расчету электрических нагрузок: РТМ 36.18.32.4-92: Утв. ВНИПИ Тяжпромэлектропроект: Введен с 01.033 / Инструктивные и информационные материалы по проектированию электроустановок. – М.: ВНИПИ Тяжпромэлектропроект, 1992. – № 6-7. – С. 4-27.
3. Электрические нагрузки промышленных предприятий / С.Д. Волобринский, Г.М. Каялов, П.Н. Клейн, Б.С. Мешель. - Л.: Энергия, 1971. - 264 с.
4. Волобринский С.Д. Электрические нагрузки и балансы промышленных предприятий. – Л.: Энергия, 1976. – 128 с.
5. Основы построения промышленных электрических сетей / Г.М. Каялов, А.Э. Каждан, И.Н.
6. Ковалев. Э.Г. Куренный / Под ред. Г. М. Каялова. - М.: Энергия, 1978. - 352 с.
Шидловский А.К., Куренный Э.Г. Введение в статистическую динамику систем электроснабжения. - К.: Наукова думка, 1984. - 271 с.
7. Жежеленко В.И., Саенко Ю.Л., Степанов В.П. Методы вероятностного моделирования в расчетах характеристик электрических нагрузок потребителей. - М.: Энергоатомиздат, 1990. -128 с.
8. Куренный Э.Г., Дмитриева Е.Н., Погребняк Н.Н. Совершенствование методов расчета электрических нагрузок // Промислова електроенергетика та електротехніка. Інформаційний збірник. - К.: ТОВ «ЕТІН». - 1997. - Випуск 4. – С. 14-28.
9. Погребняк Н.Н. Статистические решения нелинейных задач теории электрических нагрузок сетей электроснабжения промышленных предприятий. // Сборник научных трудов ДонГТУ. Серия: электротехника и энергетика, выпуск 4 - Донецк: ДонГТУ. - 1999. - С. 173-176.
10. Погребняк Н.Н. Анализ режимов сетей электроснабжения имитационными методами // Энергетика и электрификация. - 1999. - №2. - С. 22-24.
11. Погребняк Н.Н. Решение задач электроснабжения путем имитации ансамбля реализаций случайных процессов // Сборник научных трудов ДонГТУ. Серия: электротехника и энергетика, выпуск 2 - Донецк: ДонГТУ. - 1998. - С. 67-73.
12. Курінний Е.Г, Погрібняк Н.М. Інерційне енергетичне згладжування випадкових електричних процесів // Технічна електродинаміка. - 1999. - №3. - С. 54-58.
13. Погребняк Н.Н. Совершенствование методов определения расчетных электрических нагрузок по нагреву // Збірник наукових праць ДонДТУ. Серія: “Електротехніка і енергетика”, випуск 17: Донецьк: ДонДТУ, 2000. – С. 146-149.
14. Руководящий технический материал. Указания по расчету электрических нагрузок: РТМ 36.18.32.4-92: Утв. ВНИПИ Тяжпромэлектропроект: Введен с 01.033 // Инструктивные и информационные материалы по проектированию электроустановок. – М.: ВНИПИ Тяжпромэлектропроект. – 1992. – № 6-7. – С. 4-27.
|

