Меню
 Автобиография Автобиография
 Реферат Реферат
 Библиотека Библиотека
 Ссылки Ссылки
 Отчет о поиске Отчет о поиске
 Мои стихи Мои стихи
|
Автореферат выпускной работы магистра
Тема магистерской диссертации:
"Модели электрической дуги и искробезопасность"
Актуальность проблемы:
Одним из направлений решения задачи безопасности является широкое применение
искробезопасных систем передачи и использования электроэнергии. Электрические цепи таких
систем безопасны по своей природе и не нуждаются в дополнительной защите, безопасность их
не может быть нарушена по ошибке или небрежности в процессе эксплуатации.
Опыт эксплуатации искробезопасных электрических систем показал, что затраты на аппаратуру и
средства автоматизации при этом снижаются на 25-30% по сравнению с затратами на такую же
аппаратуру, взрывобезопасность которой обеспечена другими способами (заполнение оболочек
инертными средами, интенсивный продув чистым воздухом и т.д.). Однако, до настоящего времени
не создана достаточно стройная и непротиворечивая теория процесса электрического зажигания
взрывоопасных газовых смесей. Например, основные методы оценки искробезопасность основаны
на предположении о постоянстве для данной газовой смеси времени формирования ядра пламени,
а корректность такого предположения для реальных условии не доказана, отношение диаметра
минимального ядра к ширине фронта пламени по данным различных аналитических исследований
отличается почти на порядок и т.д.
Следствием такого положения является чрезмерная
трудоемкость расчетных и экспериментальных методов оценки искробезопасности электрических
цепей, использование которых сопряжено с применением корректирующих коэффициентов,
поправочных кривых и т.п., что существенно затрудняет выбор оптимальных вариантов
искробезопасной аппаратуры, максимально удовлетворяющих как технологическим требованиям,
так и требованиям безопасности.
Таким образом, одной из актуальных задач является совершенствование методов оценки
искробезопасности, электрических цепей на базе более четких представлений о характере
развития ядра пламени при электрическом зажигании в газовой среде.
Цель работы -
установление закономерностей электрического зажигания в газовой среде для определения
соотношений между параметрами электрического разряда, обеспечивающего заданную вероятность
взрыва, позволяющих повысить безопасность производства за счет совершенствования методов
оценки искробезопасности электрических цепей.
Идея работы -
определение соотношений между параметрами электрического разряда, обеспечивающего заданную
вероятность взрыва, методами математического и физического моделирования.
Предполагаемая научная новизна:
математическая модель электрического зажигания в газовой среде (представляющая собой
систему уравнений, описывающих процессы теплопроводности и движения электродов, а также
методику решения этой системы уравнений на ЭВМ), отличающаяся тем, что впервые для решения
задач электрического зажигания газовой смеси обеспечивает учет зависимости теплотехнических
свойств среды от температуры (включая тепловое расширение очага зажигания), а также
материалы, формы и скорости движения коммутирующих электродов; модель позволяет исследовать
развитие ядра пламени практически при любых реальных условиях комутации и может быть
использована для непосредственной оценки искробезопасности конкретных электрических цепей;
расчетный и электроизмерительный методы оценки искробезопасных электрических цепей,
основанные на определении воспламеняющей способности разряда во всем диапазоне его
длительностей реализуемых при испытаниях во взрывной камере, что обеспечивает повышение
надежности получаемых результатов.
ТЕПЛОВАЯ ТЕОРИЯ ВОСПЛАМЕНЕНИЯ НЕПОДВИЖНОЙ ХИМИЧЕСКИ АКТИВНОЙ ГАЗО- И ПАРОВОЗДУШНОЙ
(КИСЛОРОДНОЙ) СМЕСИ ОТ ИСКРОВОГО РАЗРЯДА
(обзор существующих исследований и разработок).
Анализ литературных данных по воспламенению горючих смесей электрическими разрядами
показывает, что в литература существуют, по сути дела, две теории воспламенения:
электрическая и тепловая.
Хотя электрические и тепловые явления в искровом разряде совместно влияют на процесс
воспламенения горючей смеси, но преобладающая роль в тепловых теориях отводится тепловому
эффекту искры, так как до настоящего времени точно не выяснено, какую роль в воспламенении
играют электрические характеристики искрового разряда, в частности создаваемая им ионизация
и, следовательно, повышенная в зоне разряда концентрация радикалов.
Электрическая или так называемая активационная теория воспламенения предполагает
специфическую способность электрического разряда к прямой химической активации, значительно
превосходящей по эффективности термическую активацию. Считается, что в зоне искрового
разряда в большом количестве образуются активные частицы типа свободных атомов и радикалов,
диффундирующие в горючую смесь и инициирующие цепную реакцию горения, которая, раз начавшись,
распространяется сама собой. Согласно этой теории условия воспламенения смеси будут зависеть
от градиента концентрации активных частиц, уходящих из области искрового разряда. За критерий
воспламенения принимается скорость реакции, которая считается зависящей от величины
разрядного тока. Эта теория разработана на основании опытов, поставленных в тлеющем разряде
при пониженном давлении. Предпринималась попытка установить на примере окисления СО, Н2 и
СН4 специфические зависимости скорости брутто-реакции не от общей энергии,
выделяемой в разряде, а от величины тока и пропорциональной ей концентрации ионизированных
частиц и их предполагаемых соединений с частицами распыленного металла катода и молекулами
воды. Изменение воспламеняющей способности разряда осуществлялось измене¬нием индуктивности
цепи, т. е. частоты и длительности разряда. Одновременно производилось калориметрирование
искровых разрядов (определялось тепло, рассеиваемое от разряда в воздух). Было замечено,
что при данном значении емкости одновременно с увеличением воспламеняющей способности
искрового разряда по мере понижения частоты (увеличения индуктивности) уменьшалось количество
тепла, которое выделялось в калориметре. По мнению Финча, такой результат исключает
возможность объяснения опытов с позиции тепловой теории.
Однако опытно доказано, что это связано с изменением энергетического баланса искрового
разряда, т. е. с перераспределением тепла, переданного от разряда воздуху (горючей смеси)
путем теплопроводности и конвекции (Wв), а также расходуемого на потери в электродах (Wэл)
и излучение (Wизл). По мере увеличения длительности разряда до известного предела повышается
воспламеняющая способность разряда вследствие уменьшения потерь на излучение; при дальнейшем
увеличении индуктивности разрядной цепи начинается уменьшение воспламеняющей способности
разряда из-за больших потерь в электроды. Подтверждается также предположение, что
воспламеняющая способность разряда в основном зависит от доли тепла, переданного разрядом
горючей смеси.
Таким образом, наблюдаются два противоположных характера зависимости воспламеняющей
способности разряда от времени. И, по-видимому, существует какой-то критический интервал
длительностей искровых разрядов, в котором воспламеняющая энергия будет оставаться
постоянной независимо от времени ее выделения.
Интересно, что сумма величин Wв+Wизл по мере роста длительности разряда непрерывно
убывает; это объясняет результат калориметрирование Финна, а именно: вследствие нагрева
стенок калориметра от серии искр он определял сумму Wв+Wизл неправильно принимая ее за
величину Wв. Результаты опытов Финча вовсе не противоречат тепловой теории,
если учесть перераспределение энергетического баланса искрового разряда при изменении параметров
разрядной цепи. С понижением частоты разряда, возможно, связано увеличение нагреваемого
объема горючей смеси. Согласно же тепловой теории, для воспламенения горючей смеси
необходимо нагреть некоторый минимальный объем (величина которого определяется свойствами
данной горючей смеси) до температуры, при которой возникает фронт пламени, способный к
самопроизвольному распространению. Свойства последнего, следовательно, должны быть
воспроизведены в начальном ядре пламени. Мерой воспламеняющей способности различных
источников тепловой энергии по этой теории может служить либо объем газа, нагреваемый за
данное время до температуры горения, либо время, необходимое для нагрева до этой
температуры определенного минимального объема газа. Эти величины определяются решением
уравнения теплопроводности Фурье при отсутствии постоянно действующих источников тепла.
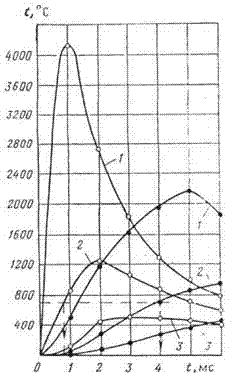 Рис. 1 - Изменение средней температуры газа при нагреве от точечного источника
(по Моргану): 1,2,3 - расстояние от источника соответственно равное 0,5; 0,75; 1 мм
Рис. 1 - Изменение средней температуры газа при нагреве от точечного источника
(по Моргану): 1,2,3 - расстояние от источника соответственно равное 0,5; 0,75; 1 мм
На рис. 1 приводятся результаты вычисления изменения во времени температуры воздуха в
объемах с различными радиусами для мгновенного и непрерывного точечных источников тепла с
одинаковым тепловыделением 0,0042 Дж. Из рис. 1 видно, что нагрев объема воздуха радиусом
0,75 мм до 700°С от мгновенного точечного источника тепла происходит за время, меньшее 1 мс,
а от источника с выделением того же количества тепла в течение 5 мс — за 4 мс. Расчет также
показывает, что за одно и то же время, например 2 мс, мгновенный источник нагревает тот же
объем до 1244°С, а непрерывный источник — только до 283°С. Все это говорит о преимущественной
воспламеняющей способности кратковременных источников тепла, например конденсированного
искрового разряда по сравнению с индукционным разрядом.
На анализе экспериментальных данных, которые подтверждают существование критического
интервала длительностей искровых разрядов, не вызывающего изменения воспламеняющей энергии,
остановимся после рассмотрения тепловых теорий воспламенения.
Различными исследователями было установлено, что в любых экспериментальных устройствах
для воспламенения горючей смеси от теплового источника (в нашем случае от искрового разряда)
необходимо выделение определенного минимального количества энергии, т. е. было установлено
наличие относительного постоянства воспламеняющей энергии на границе воспламенения.
Минимальная энергия, обеспечивающая воспламенение, и свойства «минимального»
распространяющегося ядра пламени являются, по-видимому, фундаментальными свойствами,
характеризующими природу и состояние горючей смеси при воспламенении от искрового разряда.
Минимальная энергия воспламенения приближается к физической константе (определяется только
физико-химическими свойствами смеси) и может служить характеристикой чувствительности
горючей смеси к воспламенению от электрических разрядов.
Величина энергии искровых разрядов, используемых для воспламенения горючих смесей,
обычно достаточно мала (порядка нескольких миллиджоулей), так что образовавшаяся ударная
волна затухает настолько быстро, что последующий механизм горения управляется процессом
диффузии в зависимости от характеристик переноса смеси, как в обычном случае распространения
пламени. Возмущение поля потока распространяющейся взрывной волной пренебрежимо мало, в
результате чего ядро пламени распространяется в почти невозмущенном газе.
Льюисом и Эльбе впервые была предпринята попытка теоретически рассчитать величину
минимальной энергии воспламенения. В своей трактовке минимальной энергии воспламенения они
исходили из тепловой теории распространения пламени. В зоне подогрева перед фронтом пламени
горючая смесь еще сохраняет всю свою химическую энергию и, кроме того, получает
дополнительную энергию от подогрева. Таким образом, избыточная энергия все время находится
в области фронта пламени. Согласно теории Льюиса и Эльбе, именно эта избыточная энергия и
соответствует минимальной энергии воспламенения. На основании этого для образования ядра
пламени критического диаметра, способного к самопроизвольному распространению, необходимо
создание в нем, за счет энергии искрового разряда, определенного избытка энтальпии по
сравнению с полной энтальпией свежего или сгоревшего газа. Для минимальной энергии
воспламенения получено следующее соотношение:
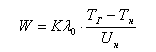 (1) (1)
где W — минимальная энергия воспламенения, Дж;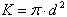 (d - критический диаметр ядра пламени — гасящее расстояние между электродами),м;
λ0 - коэффициент теплопроводности горючей смеси при
начальной температуре Тн, Вт/(м*К); ТГ — температура горения горючей
смеси, К; Тн — начальная температура горючей смеси, К; Uн —
максимальная нормальная скорость распространения пламени, м/с.
(d - критический диаметр ядра пламени — гасящее расстояние между электродами),м;
λ0 - коэффициент теплопроводности горючей смеси при
начальной температуре Тн, Вт/(м*К); ТГ — температура горения горючей
смеси, К; Тн — начальная температура горючей смеси, К; Uн —
максимальная нормальная скорость распространения пламени, м/с.
В теории Льюиса и Эльбе создание избытка энтальпии в пламени предполагается вблизи его
холодной границы, исходя из того, что кондуктивный тепловой поток 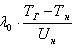 Дж/м2, значительно превосходит по скорости диффузионное перемешивание свежего и сгоревшего
газа, т. е. что,
Дж/м2, значительно превосходит по скорости диффузионное перемешивание свежего и сгоревшего
газа, т. е. что, 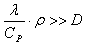 , где &rho —
плотность горючей смеси; СР — теплоемкость горючей смеси при постоянном давлении;
D — коэффициент диффузии. , где &rho —
плотность горючей смеси; СР — теплоемкость горючей смеси при постоянном давлении;
D — коэффициент диффузии.
Но это предположение не соответствует принимаемому для большинства случаев условию
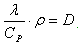 . Таким образом, теорию избытка энтальпии нет основания
принять ни как логически вытекающую из теплового механизма распространения пламени, ни в
качестве эмпирического правила, оправдываемого опытными данными по соотношению коэффициентов
температуропроводности и диффузии в пламени или по соответствию опыту вычисленных значений
энергии воспламенения. . Таким образом, теорию избытка энтальпии нет основания
принять ни как логически вытекающую из теплового механизма распространения пламени, ни в
качестве эмпирического правила, оправдываемого опытными данными по соотношению коэффициентов
температуропроводности и диффузии в пламени или по соответствию опыту вычисленных значений
энергии воспламенения.
В теории Сполдинга минимальная энергия воспламенения определяется соотношением, подобным
(1). Значение К здесь принимается равным 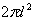 т.е. т.е.
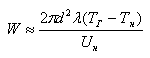 (2)
где d — удвоенная ширина зоны ламинарного пламени, м. (2)
где d — удвоенная ширина зоны ламинарного пламени, м.
Аналогичное (1) выражение для минимальной энергии воспламенения получено Розеном.
В теории Иоста для минимальной энергии воспламенения получено уравнение
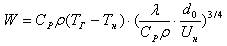 (3)
где d0 — критический диаметр ядра пламени горючей смеси, м. (3)
где d0 — критический диаметр ядра пламени горючей смеси, м.
Ввиду неопределенности величины d0 уравнение (3) не может приниматься для
расчета минимальной энергии воспламенения, однако из него можно сделать вывод, что горючая
смесь воспламеняется тем легче, чем выше эффективная скорость реакции больше Uн/d0)
и чем медленней теплоотвод из критического ядра.
Исследования Я.Б.Зельдовича показали, что представление Льюиса и Эльбе об «избыточной
энтальпии» в зоне подогрева перед фронтом пламени является ошибочным. В действительности в
зоне подогрева наряду с поступлением тепла из зоны реакции одновременно происходит
дифузионный отвод горючего в зону горения, так что суммарная внутренняя энергия смеси в зоне
подогрева остается постоянной или даже имеет слабый минимум. В принципе можно было бы
воспламенить горючую смесь, не подводя энергию извне, а вводя катализатор, способный вызвать
реакцию горения при начальной температуре. В этом случае разогрев произошел бы за счет
химической энергий смеси; полная энергия смеси не изменилась бы и, тем не менее, возникло
бы пламя.
Рассмотрим подробно тепловую модель механизма воспламенения Зельдовича как физически
наиболее наглядную и нашедшую широкое распространение. Эта модель объясняет, почему, чтобы
произошло воспламенение смеси, искровой разряд должен обладать энергией, большей, чем
минимальная энергия воспламенения.
В тепловой модели искровой разряд заменяется точечным мгновенно действующим тепловым
источником, который в момент времени t = 0 выделяет некоторое количество тепла, равное Q
джоулей.
Процесс уменьшения температуры Т на поверхности сферического объема при отсутствии
постоянно действующих источников тепла будет описываться классическим дифференциальным
уравнением нестационарной теплопроводности в декартовых координатах (уравнением Фурье):
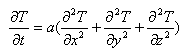 (4)
где а — коэффициент температуропроводности; t — текущая координата времени. (4)
где а — коэффициент температуропроводности; t — текущая координата времени.
Уравнение (4) для шарового объема в сферической системе координат примет вид:
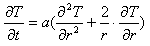 (5)
где r - расстояние от центра сферы. (5)
где r - расстояние от центра сферы.
Уравнение (5) выражает следующее: избыток тепла между теплом, вошедшим через внутреннюю и
вышедшим через внешнюю поверхность элементарного концентрического слоя, равен теплу,
накопленному в элементе за это время.
При граничных условиях 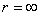 ; Т = Tн; ; Т = Tн;
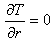 ; учитывая, что решение уравнения (5) для случая
мгновенного теплового точечного источника дано Фурье в следующем виде (кривая Гаусса): ; учитывая, что решение уравнения (5) для случая
мгновенного теплового точечного источника дано Фурье в следующем виде (кривая Гаусса):
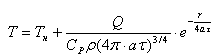 (6)
где Т — температура источника тепла; Тн — начальная температура газовой смеси;
&rho и Ср — плотность и теплоемкость смеси. Примерный характер
распределения температуры в инертном газе по истечении последовательных интервалов времени
t1,t2,. . ., tn после прекращения разряда представлен на рис. 2 сплошными линиями. Если мы
имеем горючую смесь, то процесс охлаждения замедляется вследствие тепла в окружающих искру
слоях смеси за счет развития в них химических реакций. В те же моменты времени t1, t2, . . .,
tn температуры будут выше, а объемы, занимаемые нагретым газом, несколько больше (штриховые
линии на рис. 2). (6)
где Т — температура источника тепла; Тн — начальная температура газовой смеси;
&rho и Ср — плотность и теплоемкость смеси. Примерный характер
распределения температуры в инертном газе по истечении последовательных интервалов времени
t1,t2,. . ., tn после прекращения разряда представлен на рис. 2 сплошными линиями. Если мы
имеем горючую смесь, то процесс охлаждения замедляется вследствие тепла в окружающих искру
слоях смеси за счет развития в них химических реакций. В те же моменты времени t1, t2, . . .,
tn температуры будут выше, а объемы, занимаемые нагретым газом, несколько больше (штриховые
линии на рис. 2).
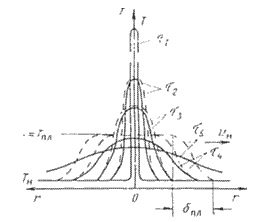 Рис. 2 - Распределение температуры вокруг мгновенного точечного источника тепла
для различных промежутков времени t1 < t2 < t3 < t4 < t5.
Рис. 2 - Распределение температуры вокруг мгновенного точечного источника тепла
для различных промежутков времени t1 < t2 < t3 < t4 < t5.
Когда температура в шаровом объеме горючей смеси упадет до значения, близкого к
температуре горения смеси ТГ, дальнейшее понижение температуры прекратится из-за
компенсации тепла, отводимого в окружающие слои смеси, теплом, выделяющимся при сгорании.
Следовательно, создадутся условия, аналогичные горению во фронте пламени. Сферический фронт
пламени состоит из зоны предварительного разогрева &deltaпл
и зоны реакции &deltaВ.
В зоне предварительного разогрева &deltaпл, составляющей
основную часть фронта пламени, свежая смесь получает тепло, необходимое для ее нагревания
до температуры горения ТГ. Это тепло за счет теплопроводности поступает из зоны,
в которой протекает химическая реакция. Чем меньше радиус начального ядра горящего газа, тем
больше отношение количества тепла, покидающего сферический объем (оно пропорционально
квадрату радиуса), к количеству тепла, возникающего в этом объеме (оно пропорционально
кубу радиуса). Следовательно, должно существовать какое-то критическое значение радиуса
rкр, ниже которого прирост тепла, образующегося в зоне реакции, недостаточен
для нагрева поступающей в зону реакции свежей смеси до температуры ТГ. Недостающая
энергия может быть получена только от источника воспламенения.
Из тепловой теории распространения ламинарного пламени известно, что химическая реакция
идет со скоростью, необходимой для поддержания горения, только в пределах довольно узкого
характеристического интервала температур θ. Следовательно,
распространение пламени возможно только при условии, что время охлаждения tохл
газового объема от температуры ТГ до температуры ТГ - θ
будет больше или в предельном случае равно времени химической реакции tр 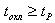 (7) (7)
Величину tохл можно определить из выражения (6), подставляя в него
T = TГ - &theta при r = 0. Для расчета tохл была
использована приближенная линейная аппроксимация функции (6), Тmax = f(t) при r = 0.
Применяя аппроксимацию в точке, где Тmax=ТГ, получим выражение для
критерия воспламенения.
Время охлаждения
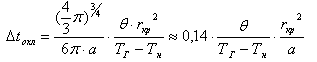 (8) (8)
Время реакции tp в зоне пламени по порядку величины (с учетом коэффициента
пропорциональности):
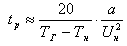 (9) (9)
Совместное решение уравнений (8) и (9) относительно rкр с учетом того, что
характерная ширина зоны ламинарного пламени
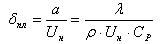 (10)
дает (10)
дает
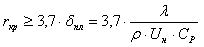 (11) (11)
Таким образом, критические условия воспламенения искрой сводятся к нагреванию газовой
сферы, радиус которой почти вчетверо превышает ширину зоны ламинарного пламени в
рассматриваемой горючей смеси, до температуры пламени за счет тепловой энергии разряда. При
этом условии близлежащие слои горючей смеси успеют воспламениться прежде, чем остынет
нагретый искрой объем.
Сферический фронт пламени при значениях r >> rкр способен к дальнейшему
самостоятельному распространению; при значениях r < rкр пламя затухает, так как
отдача тепла в окружающие слои газа превышает тепло, выделяющееся за счет сгорании.
Для большинства углеводородно-воздушных смесей коэффициент температуропроводности близок
к коэффициенту температуропроводности воздуха и мало зависит от состава и природы топлива.
Соотношение (11) можно рассматривать только как качественную связь между воспламеняющей
энергией искрового разряда и параметрами горючей смеси. Полученное в (11) значение
коэффициента пропорциональности указывает только на порядок этой величины, учитывая
приближенность допущений, принятых при выводе формулы (СР=const и др.). Таким
образом, окончательная проверка соотношения (11) может быть сделана только экспериментальным
путем.
Анализ тепловых теорий показал, что различие рассмотренных моделей воспламенения
заключается в выборе элемента сходства ядра воспламенения с фронтом пламени: в схеме
Зельдовича и Сполдинга критический диаметр ядра воспламенения принимается пропорциональным
ширине зоны пламени; в схеме Иоста объемная скорость тепловыделения в ядре воспламенения
принимается равной этой величине во фронте пламени; в схеме Льюиса и Эльбе предполагается
наличие избытка энтальпии в ядре воспламенения по сравнению с полной энтальпией свежего или
сгоревшего газа.
Из рассмотрения теорий воспламенения горючих смесей от искрового разряда видно, что по
активационной (электрической) теории воспламенения необходимо создание такой ионизации газа
в разрядном промежутке, чтобы обеспечить протекание возможно большего тока по искровому
каналу. Это заключение согласуется с выводом тепловой теории об обеспечении нагрева
некоторого минимального объема горючей смеси. Протекание большого тока по искровому каналу
означает увеличение поперечных размеров искрового канала, т. е. увеличение объема горючей
смеси, вступающей в реакцию.
Кроме рассмотренных выше классических работ по воспламенению горючих газо-, паровоздушных
смесей искровыми разрядами, интерес представляют также тепловые модели воспламенения
Фепна, Япга, Гришина. В этих работах получены выражения для минимальной энергии воспламенения,
показано влияние различных физических параметров на величину энергии воспламенения. Однако
сравнение с экспериментом весьма затруднительно ввиду того, что отсутствуют числовые значения
физических параметров и прежде всего значения энергии активации для воспламенения искровым
разрядом.
Нерешенные проблемы:
Основной трудностью при создании математической модели электрической дуги является
необходимость учета изменения газовых характеристик с изменением температуры, а так же
ряд других сходных проблем. Вследствие чего, при создании математической модели принимаются
следующие допущения:
- Считаем, что в областях, не занятых искрой, тепловые свойства газовой смеси,
подчиняются аппроксимирующим зависимостям, полученным по данным.
- Распределение температуры определяется решением нестационарного уравнения теплопроводности
в сферических координатах.
- Дуговой столб имеет цилиндрическую форму, а температура по радиусу столба изменяется в
соответствии с рассчитанной по "методу источника"
Собственные результаты:
С помощью пакета MathCad создана программа, реализующая на ЭВМ модель зажигания
метаново-воздушной смеси от маломощного искрового разряда.
Результаты данной программы представлены на рис.3, на котором представлены кривые распределения
температуры по радиусу искры от величины m*Δ, где m изменяется от 0 до М, М - это
количество точек на графике, Δ = 1/M, для моментов времени 0; 100; 200 и 500 мс.
Мощность разряда составляет 5 Вт.
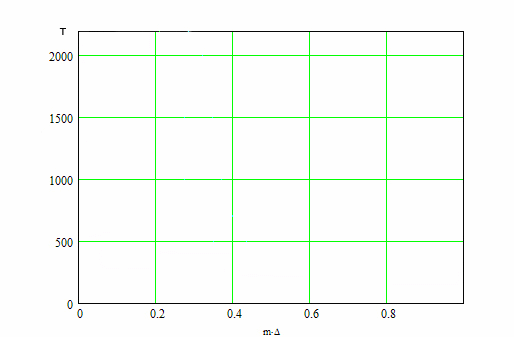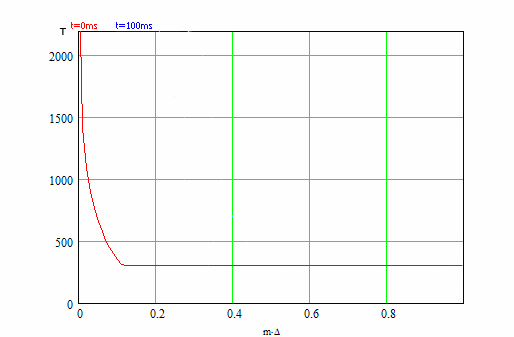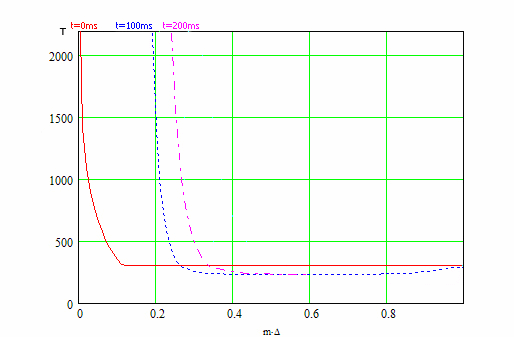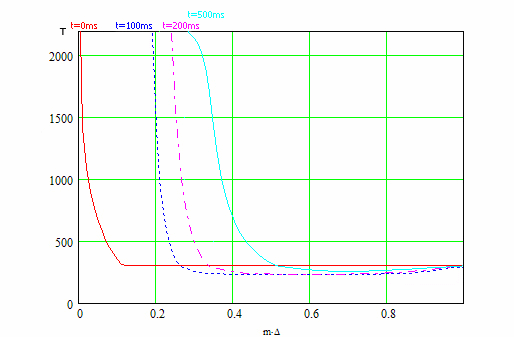 Рис. 3 - Анимированный график зависимостей температуры от радиуса распределения искры
для моментов времени 0; 100; 200 и 500 мс.
Рис. 3 - Анимированный график зависимостей температуры от радиуса распределения искры
для моментов времени 0; 100; 200 и 500 мс.
Заключение:
В моей магистерской работе будет представлена программа, созданная в пакете MathCad, с помощью
которой можно будет определять соотношение между параметрами электрического разряда,
обеспечивающего заданную вероятность взрыва и параметрами электрической цепи. Это значительно
облегчит расчет оценки искробезопасности электрических цепей, а также выбор оптимальных
вариантов искробезопасной аппаратуры. На данный момент это будет наиболее точная
математическая модель электрического зажигания в газовой среде, обеспечивающая учет
зависимости теплотехнических свойств среды от температуры, материалы, формы и скорости
движения коммутирующих электродов и позволяющая исследовать развитие ядра пламени практически
при любых реальных условиях комутации.
В настоящее время (май 2006) магистерская работа надодится в стадии разработки.
Окончательный вариант будет в январе 2007 г. За справками обращаться к автору или руководителю.
Литература
- Бершадский И.А., Клименко М.С. Моделирование очагового
зажигания взрывоопасной газовой смеси с учетом заданной мощности тепловых источников искрового разряда. ДонНТУ, кафедра
"Электроснабжение промышленных предприятий и городов", 2006.
- Ерыгин А.Т., Трембицкий А.П. Методы оценки искробезопасности электрических цепей. – М.:
Наука, 1984. 256 с.
- Таев И.С. Электрические аппарты. Общая теория. М., «Энергия», 1977. 228 с.
- Лелевкин В.М., Семенов В.Ф. Численное моделирование характерестик открытой
диафрагмированной электрической дуги
- Коган А.Г. Электроизмерительная и расчетная оценка искробезопасности индуктивных
электрических цепей на основе математической модели очагового зажигания рудничных газов:
Автореф. дис … к.т.н. Макеевка: МакНИИ, 1988.
|