Биография | Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание
Оглавление
Доступность методов записи и хранения данных привели к бурному росту объемов хранимых данных. Объемы данных настолько внушительны, что человеку просто не по силам проанализировать их. Хотя необходимость проведения такого анализа вполне очевидна, ведь в этих 'сырых данных' заключены знания, которые могут быть использованы при принятии решений. Для того, чтобы провести автоматический анализ данных, используется Data Mining.
Data Mining – это процесс обнаружения в 'сырых' данных ранее неизвестных нетривиальных практически полезных и доступных интерпретации знаний, необходимых для принятия решений в различных сферах человеческой деятельности. Data Mining – является одним из шагов Knowledge Discovery in Databases.
Информация, найденная в процессе применения методов Data Mining, должна быть нетривиальной и ранее неизвестной. Знания должны описывать новые связи между свойствами, предсказывать значения одних признаков на основе других и т.д. Найденные знания должны быть применимы и на новых данных с некоторой степенью достоверности. Полезность заключается в том, чтобы эти знания могли принести определенную выгоду при их применении. Знания должны быть в понятном для пользователя-нематематика виде. Например, проще всего воспринимаются человеком логические конструкции 'если … то …'.
Алгоритмы, используемые в Data Mining, требуют большого количества вычислений. Раньше это являлось сдерживающим фактором широкого практического применения Data Mining, однако сегодняшний рост производительности современных процессоров снял остроту этой проблемы. Теперь за приемлемое время можно провести качественный анализ сотен тысяч и миллионов записей.
Мощные компьютерные системы, хранящие и управляющие огромными базами данных, стали неотъемлемым атрибутом жизнедеятельности как крупных корпораций, так и даже небольших компаний. Тем не менее, наличие данных само по себе еще недостаточно для улучшения показателей работы. Нужно уметь трансформировать сырые данные в полезную для принятия решений информацию. В этом и состоит основное предназначение технологий Data Mining.
Исследования различных методов извлечения знаний. Предполагаетсся сравнение некоторых модификаций деревьев решений и генетического алгоритма. Для сравнения эффективности разрабатывается система извлечения знаний, которая будет извлекать знания указанными выше меотдами. Возможным завершением работы может стать разработка нового метода состоящего в комбинации или модификации уже извесных методов.
Научная новизна состоит в проведении глубокого анализа качества извлеченных знаний, оценки быстроты и точности работы алгоритмов. Выбора наилучшего алгоритма для проектируемой системы. А также создания так новой модификации метода деревьев решений на основе CART.
Практическая ценность данной работы заключается в анализе существующих методов извлечения знаний. Выбора наиболее оптимального метода или модификация существующих методов для извлечения знаний наиболее полно отражающих характер входных данных. Не маловажнную роль играет и скорость извлечения знаний. Во-первых базы данных обладают невероятными размерами(до 850 гигабайт). Во-вторых, извлечение в некоторых системах должно происходить в режиме реального времени. В-третьих большинство современных баз данных являются распределенными. Для этого преполагается создание распределенной системы извлечения знаний орирентированную на работу с удаленными базами данных.
Data Mining переводится как «добыча» или «раскопка данных»[1]. Синонимами Data Mining являются также термины «обнаружение знаний в базах данных» (knowledge discovery in databases) и «интеллектуальный анализ данных». Возникновение всех этих терминов связано с новым витком в развитии средств и методов обработки данных.
Необходимость обработки данных обусловлена тем, что в связи с совершенствованием технологий записи и хранения данных собрались колоссальные потоки информации в самых различных областях. Деятельность любого предприятия (коммерческого, производственного, медицинского, научного и т. д.) теперь сопровождается регистрацией и записью всех подробностей его деятельности.
Сфера применения Data Mining ничем не ограничена - она везде, где имеются какие-либо данные. Но в первую очередь методы Data Mining сегодня, мягко говоря, заинтриговали коммерческие предприятия, развертывающие проекты на основе информационных хранилищ данных (Data Warehousing). Опыт многих таких предприятий показывает, что отдача от использования Data Mining может достигать 1000%. Например, известны сообщения об экономическом эффекте, в 10-70 раз превысившем первоначальные затраты от 350 до 750 тыс. дол. [19]. Известны сведения о проекте в 20 млн. дол., который окупился всего за 4 месяца. Другой пример - годовая экономия 700 тыс. дол. за счет внедрения Data Mining в сети универсамов в Великобритании.
Data Mining представляют большую ценность для руководителей и аналитиков в их повседневной деятельности. Деловые люди осознали, что с помощью методов Data Mining они могут получить ощутимые преимущества в конкурентной борьбе. Кратко охарактеризуем некоторые возможные бизнес-приложения Data Mining [2].
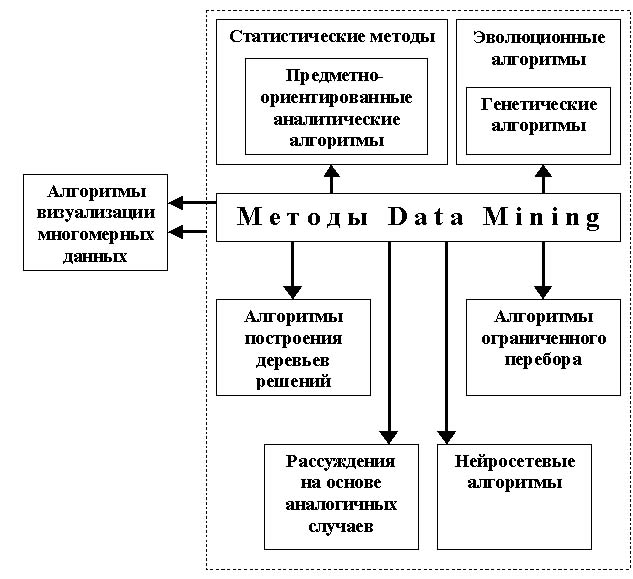
Data Mining является мультидисциплинарной областью, возникшей и развивающейся на базе достижений прикладной статистики, распознавания образов, методов искусственного интеллекта, теории баз данных и др. Отсюда обилие методов и алгоритмов, реализованных в различных действующих системах Data Mining [1, 2, 16]. Многие из таких систем интегрируют в себе сразу несколько подходов. Тем не менее, как правило, в каждой системе имеется какой-то ключевой компонент, благодаря которому можно выделить следующие классы алгоритмов [17] (рисунок 1):

Рисунок 1 – Классы алгоритмов Data Mining
Предметно-ориентированные аналитические системы очень разнообразны. Наиболее широкий подкласс таких систем, получивший распространение в области исследования финансовых рынков, носит название «технический анализ». Он представляет собой совокупность нескольких десятков методов прогноза динамики цен и выбора оптимальной структуры инвестиционного портфеля, основанных на различных эмпирических моделях динамики рынка.[17,18] Эти методы часто используют несложный статистический аппарат, но максимально учитывают сложившуюся в своей области специфику (профессиональный язык, системы различных индексов и пр.)
Последние версии почти всех известных статистических пакетов включают наряду с традиционными статистическими методами также элементы Data Mining. Но основное внимание в них уделяется все же классическим методикам - корреляционному, регрессионному, факторному анализу и др.[9] Недостатком систем этого класса считают требование к специальной подготовке пользователя. Также отмечают, что мощные современные статистические пакеты являются слишком «тяжеловесными» для массового применения в финансах и бизнесе[18, 9].
Есть еще более серьезный принципиальный недостаток статистических пакетов, ограничивающий их применение в Data Mining. Большинство методов, входящих в состав пакетов, опираются на статистическую парадигму, в которой главными фигурантами служат усредненные характеристики выборки. А эти характеристики при исследовании реальных сложных жизненных феноменов часто являются фиктивными величинами [1].
Нейронные сети – это большой класс систем, архитектура которых имеет аналогию с построением нервной ткани из нейронов. В одной из наиболее распространенных архитектур, многослойном персептроне с обратным распространением ошибки, имитируется работа нейронов в составе иерархической сети, где каждый нейрон более высокого уровня соединен своими входами с выходами нейронов нижележащего слоя. На нейроны самого нижнего слоя подаются значения входных параметров, на основе которых нужно принимать какие-то решения, прогнозировать развитие ситуации и т. д. Эти значения рассматриваются как сигналы, передающиеся в следующий слой, ослабляясь или усиливаясь в зависимости от числовых значений (весов), приписываемых межнейронным связям. В результате на выходе нейрона самого верхнего слоя вырабатывается некоторое значение, которое рассматривается как ответ — реакция всей, сети на введенные значения входных параметров. Для того чтобы сеть можно было применять в дальнейшем, ее прежде надо «натренировать» на полученных ранее данных, для которых известны и значения входных параметров, и правильные ответы на них. Тренировка состоит в подборе весов межнейронных связей, обеспечивающих наибольшую близость ответов сети к известным правильным ответам.[12, 5]
Основным недостатком нейросетевой парадигмы является необходимость иметь очень большой объем обучающей выборки. Другой существенный недостаток заключается в том, что даже натренированная нейронная сеть представляет собой «черный ящик». Знания, зафиксированные как веса нескольких сотен межнейронных связей, совершенно не поддаются анализу и интерпретации человеком [2].
Деревья решений – это способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение[1, 21].
Под правилом понимается логическая конструкция, представленная в виде «если … то …».

Рисунок 2 – Пример построения дерева решений (Анимация 3 Кб)
Область применения деревья решений в настоящее время широка, но все задачи, решаемые этим аппаратом могут быть объединены в следующие три класса[21]:
Пусть нам задано некоторое обучающее множество T, содержащее объекты (примеры), каждый из которых характеризуется m атрибутами (атрибутами), причем один из них указывает на принадлежность объекта к определенному классу.
Идею построения деревьев решений из множества T, впервые высказанную Хантом, приведем по Р. Куинлену (R. Quinlan)[20].
Пусть через {C1, C2, … Ck} обозначены классы(значения метки класса), тогда существуют 3 ситуации:
Вышеописанная процедура лежит в основе многих современных алгоритмов построения деревьев решений, этот метод известен еще под названием разделения и захвата (divide and conquer). Очевидно, что при использовании данной методики, построение дерева решений будет происходит сверху вниз.
Поскольку все объекты были заранее отнесены к известным нам классам, такой процесс построения дерева решений называется обучением с учителем (supervised learning). Процесс обучения также называют индуктивным обучением или индукцией деревьев (tree induction)[21].
На сегодняшний день существует значительное число алгоритмов, реализующих деревья решений CART, C4.5, NewId, ITrule, CHAID, CN2 и т.д. Но наибольшее распространение и популярность получили следующие два:
CART (Classification and Regression Tree) – это алгоритм построения бинарного дерева решений – дихотомической классификационной модели. Каждый узел дерева при разбиении имеет только двух потомков. Как видно из названия алгоритма, решает задачи классификации и регрессии.
C4.5 – алгоритм построения дерева решений, количество потомков у узла не ограничено. Не умеет работать с непрерывным целевым полем, поэтому решает только задачи классификации[20].
Большинство из известных алгоритмов являются «жадными алгоритмами». Если один раз был выбран атрибут, и по нему было произведено разбиение на подмножества, то алгоритм не может вернуться назад и выбрать другой атрибут, который дал бы лучшее разбиение. И поэтому на этапе построения нельзя сказать даст ли выбранный атрибут, в конечном итоге, оптимальное разбиение.
Рассмотрев основные проблемы, возникающие при построении деревьев, было бы несправедливо не упомянуть об их достоинствах:
Деревья решений являются прекрасным инструментом в системах поддержки принятия решений, интеллектуального анализа данных (data mining)[21,22].
В состав многих пакетов, предназначенных для интеллектуального анализа данных, уже включены методы построения деревьев решений. В областях, где высока цена ошибки, они послужат отличным подспорьем аналитика или руководителя
Деревья решений успешно применяются для решения практических задач в следующих областях:
Это далеко не полный список областей где можно использовать деревья решений. Не исследованы еще многие потенциальные области применения.
Алгоритмы ограниченного перебора были предложены в середине 60-х годов М. М. Бонгардом для поиска логических закономерностей в данных[3]. С тех пор они продемонстрировали свою эффективность при решении множества задач из самых различных областей [7].
Эти алгоритмы вычисляют частоты комбинаций простых логических событий в подгруппах данных [1]. Примеры простых логических событий: X = а; X < а; X > а; a < X < b и др., где X — какой либо параметр, а и b — константы. Одна из опасностей при построении описания - возможность возникновения так называемых предрассудков, т.е. отбора условий, удовлетворяющих предъявленным требованиям лишь на обучающей выборке и оказывающихся бесполезными за ее пределами. По-видимому, первым, кто обратил внимание на эту проблему, был М.М.Бонгард [3]; ему же принадлежит и термин "предрассудок".
Ясно, что увеличивая пороги вероятности ошибки первого рода и уменьшая вероятности ошибки второго рода, мы уменьшаем вероятность возникновения предрассудков. Однако, актуальной остается проблема выбора порогов, гарантирующих, что вероятность появления хотя бы даже одного предрассудка не превосходит заданной величины. В работе [7] предложен один из возможных подходов, эксплуатирующий фактически идею "хаотизации" (или "перемешивания") И.Ш.Пинскера [8]. Перемешивание используется для определения достаточности объема обучающей выборки при поиске решающего правила из заданного класса. Принцип основан на случайном распределении объектов обучающей выборки по классам, при котором учитываются лишь априорные вероятности классов, если они доступны. Если после этого в результате обучения будет найдено достаточно хорошее решающее правило, считается, что объем обучающей выборки недостаточен для надежного выбора. В работе В.Е.Голендера и А.Б.Розенблита[7] предложено по "перемешанным" выборкам оценить распределения каких-либо характеристик условий и отбирать признаки, используя пороги, при выборе которых учтены эти распределения. Этот подход, содержательно вполне оправданный, остается, тем не менее, вполне эвристическим и не позволяет получить оценку вероятности проникновения предрассудков в совокупность отобранных условий.
Ограничением служит длина комбинации простых логических событий. На основании анализа вычисленных частот делается заключение о полезности той или иной комбинации для установления ассоциации в данных, для классификации, прогнозирования и т.п.
Идея систем рассуждений на основе аналогичных случаев (case based reasoning – CBR) – на первый взгляд крайне проста. Для того чтобы сделать прогноз на будущее или выбрать правильное решение, эти системы находят в прошлом близкие аналоги наличной ситуации и выбирают тот же ответ, который был для них правильным. Поэтому этот метод еще называют методом «ближайшего соседа» (nearest neighbour). В последнее время распространение получил также термин memory based reasoning, который акцентирует внимание на том, что решение принимается на основании всей информации, накопленной в памяти [1].
Системы CBR показывают неплохие результаты в самых разнообразных задачах. Главным их минусом считают то, что они вообще не создают каких-либо моделей или правил, обобщающих предыдущий опыт, - в выборе решения они основываются на всем массиве доступных исторических данных, поэтому невозможно сказать, на основе каких конкретно факторов CBR-системы строят свои ответы.
Другой минус заключается в произволе, который допускают системы CBR при выборе меры «близости». От этой меры самым решительным образом зависит объем множества прецедентов, которые нужно хранить в памяти для достижения удовлетворительной классификации или прогноза[1].
Генетические алгоритмы предназначены для решения задач оптимизации. Примером подобной задачи может служить обучение нейросети, то есть подбора таких значений весов, при которых достигается минимальная ошибка. При этом в основе генетического алгоритма лежит метод случайного поиска. Основным недостатком случайного поиска является то, что нам неизвестно сколько понадобится времени для решения задачи. Для того, чтобы избежать таких расходов времени при решении задачи, применяются методы, проявившиеся в биологии. При этом используются методы открытые при изучении эволюции и происхождения видов. Как известно, в процессе эволюции выживают наиболее приспособленные особи. Это приводит к тому, что приспособленность популяции возрастает, позволяя ей лучше выживать в изменяющихся условиях.
Впервые подобный алгоритм был предложен в 1975 году Джоном Холландом (John Holland) в Мичиганском университете. Он получил название «репродуктивный план Холланда» и лег в основу практически всех вариантов генетических алгоритмов. [24]
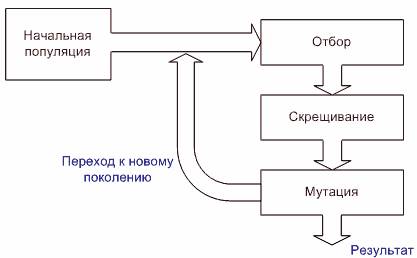
Рисунок 3 - Алгоритм работы классического генетического алгоритма
Из биологии мы знаем, что любой организм может быть представлен своим фенотипом, который фактически определяет, чем является объект в реальном мире, и генотипом, который содержит всю информацию об объекте на уровне хромосомного набора. При этом каждый ген, то есть элемент информации генотипа, имеет свое отражение в фенотипе. Таким образом, для решения задач нам необходимо представить каждый признак объекта в форме, подходящей для использования в генетическом алгоритме. Все дальнейшее функционирование механизмов генетического алгоритма производится на уровне генотипа, позволяя обойтись без информации о внутренней структуре объекта, что и обуславливает его широкое применение в самых разных задачах.
В наиболее часто встречающейся разновидности генетического алгоритма для представления генотипа объекта применяются битовые строки. При этом каждому атрибуту объекта в фенотипе соответствует один ген в генотипе объекта. Ген представляет собой битовую строку, чаще всего фиксированной длины, которая представляет собой значение этого признака.
Как известно в теории эволюции важную роль играет то, каким образом признаки родителей передаются потомкам. В генетических алгоритмах за передачу признаков родителей потомкам отвечает оператор, который называется скрещивание (его также называют кроссовер или кроссинговер). [23, 1]Этот оператор определяет передачу признаков родителей потомкам. Действует он следующим образом:
Рассмотрим функционирование этого оператора:
Хромосома_1: |
0000000000 |
Хромосома_2: |
1111111111 |
Рисунок 4 – Начальное состяние хромосом
Допустим разрыв происходит после 3-го бита хромосомы(рис 4), тогда результат работы оператора будет представлен на рисунке 5.
Хромосома_1: |
0000000000 |
>> |
000 |
1111111 |
Результ_хромосома_1 |
Хромосома_2: |
1111111111 |
>> |
111 |
0000000 |
Результ_хромосома_2 |
Рисунок 5 – Результат действия оператора скрещивание
Затем с вероятностью 0,5 определяется одна из результирующих хромосом в качестве потомка. Следующий генетический оператор предназначен для того, чтобы поддерживать разнообразие особей с популяции. Он называется оператором мутации. При использовании данного оператора каждый бит в хромосоме с определенной вероятностью инвертируется[23].
Кроме того, используется еще и так называемый оператор инверсии, который заключается в том, что хромосома делится на две части, и затем они меняются местами. Схематически это можно представить следующим образом(рис 6)
| 000 |
1111111 |
>> |
1111111 |
000 |
Рисунок 6 – Схема работы оператора инверсии
В принципе для функционирования генетического алгоритма достаточно этих двух генетических операторов, но на практике применяют еще и некоторые дополнительные операторы или модификации этих двух операторов. Например, кроссовер может быть не одноточечный (как было описано выше), а многоточечный, когда формируется несколько точек разрыва (чаще всего две). Кроме того, в некоторых реализациях алгоритма оператор мутации представляет собой инверсию только одного случайно выбранного бита хромосомы.
Теперь, зная как интерпретировать значения генов, перейдем к описанию функционирования генетического алгоритма. Рассмотрим схему функционирования генетического алгоритма в его классическом варианте[23].
Эволюционное программирование основано на формулировании гипотезы о виде зависимости целевой переменной от других переменных в виде программ на некотором внутреннем языке программирования. Процесс построения программ строится как эволюция в мире программ (этим подход немного похож на генетические алгоритмы). Когда система находит программу, более или менее удовлетворительно выражающую искомую зависимость, она начинает вносить в нее небольшие модификации и отбирает среди построенных дочерних программ те, которые повышают точность. Таким образом, система «выращивает» несколько генетических линий программ, которые конкурируют между собой в точности выражения искомой зависимости. Специальный модуль переводит найденные зависимости с внутреннего языка системы на понятный пользователю язык (математические формулы, таблицы и пр.) [2].
Другое направление эволюционного программирования связано с поиском зависимости целевых переменных от остальных в форме функций какого-то определенного вида. Например, в одном из наиболее удачных алгоритмов этого типа – методе группового учета аргументов (МГУА) — зависимость ищут в форме полиномов.
Средства для визуализации многомерных данных поддерживаются всеми системами Data Mining. Вместе с тем, весьма внушительную долю рынка занимают системы, специализирующиеся исключительно на этой функции.
В подобных системах основное внимание сконцентрировано на дружелюбии пользовательского интерфейса, позволяющего ассоциировать с анализируемыми показателями различные параметры диаграммы рассеивания объектов (записей) базы данных. К таким параметрам относятся цвет, форма, ориентация относительно собственной оси, размеры и другие свойства графических элементов изображения. Кроме того, системы визуализации данных снабжены удобными средствами для масштабирования и вращения изображений[1].
Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики. Данные понятия были впервые предложены американским ученым Лотфи Заде (Lotfi Zadeh) в 1965 г. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.[13,14,16]
Прежде чем нечеткий подход к моделированию сложных систем получил признание во всем мире, прошло не одно десятилетие с момента зарождения теории нечетких множеств. И на этом пути развития нечетких систем принято выделять три периода.
Первый период (конец 60-х–начало 70 гг.) характеризуется развитием теоретического аппарата нечетких множеств (Л. Заде, Э. Мамдани, Беллман). Во втором периоде (70–80-е годы) появляются первые практические результаты в области нечеткого управления сложными техническими системами (парогенератор с нечетким управлением). Одновременно стало уделяться внимание вопросам построения экспертных систем, построенных на нечеткой логике, разработке нечетких контроллеров. Нечеткие экспертные системы для поддержки принятия решений находят широкое применение в медицине и экономике. Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечетких экспертных систем, а области применения нечеткой логики заметно расширяются. Она применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений и многих других.[14]
Триумфальное шествие нечеткой логики по миру началось после доказательства в конце 80-х Бартоломеем Коско знаменитой теоремы FAT (Fuzzy Approximation Theorem) [13]. В бизнесе и финансах нечеткая логика получила признание после того как в 1988 году экспертная система на основе нечетких правил для прогнозирования финансовых индикаторов единственная предсказала биржевой крах. И количество успешных фаззи-применений в настоящее время исчисляется тысячами.
Характеристикой нечеткого множества выступает функция принадлежности (Membership Function). Обозначим через MFc(x)– степень принадлежности к нечеткому множеству C, представляющей собой обобщение понятия характеристической функции обычного множества. Тогда нечетким множеством С называется множество упорядоченных пар вида C={MFc(x)/x}, MFc(x) принадлежит [0,1]. Значение MFc(x)=0 означает отсутствие принадлежности к множеству, 1– полную принадлежность[14].
Для нечетких множеств, как и для обычных, определены основные логические операции. Самыми основными, необходимыми для расчетов, являются пересечение и объединение.
Пересечение двух нечетких множеств (нечеткое "И"): A пересечение B: MFAB(x)=min(MFA(x), MFB(x)). Объединение двух нечетких множеств (нечеткое "ИЛИ"): A объединение B: MFAB(x)=max(MFA(x), MFB(x)).
В теории нечетких множеств разработан общий подход к выполнению операторов пересечения, объединения и дополнения, реализованный в так называемых треугольных нормах и конормах. Приведенные выше реализации операций пересечения и объединения;– наиболее распространенные случаи t-нормы и t-конормы.[14]
Для описания нечетких множеств вводятся понятия нечеткой и лингвистической переменных.
Нечеткая переменная описывается набором (N,X,A), где N– это название переменной, X– универсальное множество (область рассуждений), A– нечеткое множество на X. Значениями лингвистической переменной могут быть нечеткие переменные, т.е. лингвистическая переменная находится на более высоком уровне, чем нечеткая переменная[14,15]. Каждая лингвистическая переменная состоит из:
Основой для проведения операции нечеткого логического вывода является база правил, содержащая нечеткие высказывания в форме 'Если-то' и функции принадлежности для соответствующих лингвистических термов[14,15]. При этом должны соблюдаться следующие условия:
Существует хотя бы одно правило для каждого лингвистического терма выходной переменной.
Для любого терма входной переменной имеется хотя бы одно правило, в котором этот терм используется в качестве предпосылки (левая часть правила).
В противном случае имеет место неполная база нечетких правил.
Пусть в базе правил имеется m правил (рис. 2.7), где xk , k=1..n;– входные переменные; y;– выходная переменная; Aik;– заданные нечеткие множества с функциями принадлежности.

Рисунок 7 - Нечеткие правила
Результатом нечеткого вывода является четкое значение переменной y* на основе заданных четких значений xk , k=1..n.
В общем случае механизм логического вывода включает четыре этапа[14]: введение нечеткости (фазификация), нечеткий вывод, композиция и приведение к четкости, или дефазификация (см. рисунок 2.8).
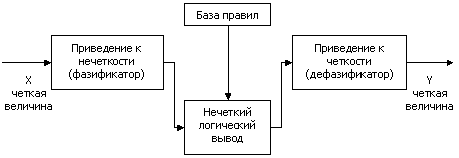
Рисунок 8. Система нечеткого логического вывода.
Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностью метода дефазификации. Разработаны модели нечеткого вывода Мамдани, Сугено, Ларсена, Цукамото.
В результате данной научной работы был проведен анализ существующих методов и систем автоматического извлечения знаний. Опираясь на существующую конъюнктуру рынка программного обеспечения, был сделан вывод о целесообразности создания подобной системы, но с учетом недостатков предыдущих систем:
Анализ множества методов извлечения знаний были неприемлемость некоторых методов. Так нейросетевые алгоритмы хоть и извлекают знания из данных, однако хранят их в неприемлемой и мало понятной форме. Статистические пакеты со своими методами также не подходят для извлечения скрытых данных, так как они скорее подгоняют правила к данным, а не пытаются найти скрытые закономерности. Как наиболее простой способ, дающий отличные результаты при анализе данных был выбран метод деревьев решений. Этот метод хорошо зарекомендовал себя как надежный, простой в реализации. Генетический алгоритм также очень перспективный способ извлечения знаний, однако, из-за того факта, что алгоритм дает прекрасные результаты на одной предметной области и может привести к тупиковой ветви на другой предметной области, этот алгоритм не будет реализовываться в последующей магистерской работе.
Анализ существующего рынка программных средств извлечения знаний дал возможность оценить достоинства и недостатки существующих методов, проверить эффективность различных реализованных методов извлечения знаний.
Внимание!!
При написании данного автореферата магистерская работа еще не завершена. Окончательное завершение исследований планируется до 01.01.2007. Полный текст работы и все материалы по теме могут быть получены у автора или его руководителя после указанной даты.