Автореферат по теме выпускной магистерской работы
Прогнозирование уровня подземных вод в Донецкой области с использованием нейросетевых технологий
Содержание
Введение
Методы исследований
Анализ временных рядов и прогнозирование (программный пакет STATISTICA)
Метод авторегрессии и проинтегрированного скользящего среднего (ARIMA - АРПСС)
Применение нейросетевых технологий
Заключение
Список источников
|
Введение
В настоящее время вопрос эффективного применения вычислительной техники для решения различных задач моделирования и прогнозирования в экологии и климатологии принял широкое распространение и стал актуальным. Особенность данных проблемных областей заключается в малом числе теоретически обоснованных и хорошо согласующихся с реальными данными вычислительных моделей.
Поэтому прикладные задачи часто решаются на основе моделей, построенных по таблицам экспериментальных данных. При этом проблему представляет как сложность учета всех факторов, влияющих на ситуацию в конкретных территориях, так и сложность сбора территориально распределенной информации.
Индустриализация в Донбассе ускорила развитие опасных эколого-геологических процессов, повлиявших на состояние природной среды. Особенно остро эта проблема стала ощущаться с началом реструктуризации угледобывающей отрасли.
Экологическая ситуация в Донбассе стала угрожающей. Ликвидация угольных шахт, которая осуществлялась и до сих пор осуществляется без учета прогнозных оценок экологических последствий и с частыми нарушениями природоохранного законодательства в условиях финансирования по остаточному принципу, приводит к существенному осложнению экологической ситуации в угледобывающих регионах.
Среди природно-техногенных процессов, вызванных массовым закрытием шахт, можно выделить такие как: поступление минерализованных шахтных вод в подземные и поверхностные водные объекты и их загрязнение, ускорение миграции техногенных загрязнений в геологическую среду и биологические объекты; подтопление и заболачивание земельных угодий и территорий промышленно-гражданской застройки и другие.
С резким возрастанием притоков подземных вод в шахты в период массового закрытия и изменения их уровня, а также вследствие увеличения числа техногенных источников загрязнения проблема охраны и восстановления качества ресурсов подземных вод на территориях, прилегающих к зонам влияния закрытых шахт, еще более обострилась.
Практического опыта по борьбе с капризами природы у современных инженеров не так уж и много, поскольку раньше бесперебойную работу угольных предприятий гарантировала регулярная откачка подземных вод. Поэтому в настоящее время актуально разработать информационно аналитическую систему и сделать прогноз уровней подземных вод в Донецкой области.
Целью данной работы является повышение гидрогеологической безопасности на территории Донецкой области на базе установления системных закономерностей в изменениях водоносных горизонтов с использованием нейросетевых технологий.
Предметом исследования являются модели изменения уровней подземных вод на базе нейросетевых технологий.
Объект исследования – процессы изменения уровня подземных вод на территории Донецкой области.
Практическая значимость работы:
- отобраны и проанализированы классические, наиболее популярные статистические методы прогнозирования;
- исследованы современные методы прогнозирования, основанные на нейронных сетях;
- исследован существующий программный пакет Statistica;
- практическая значимость работы заключается в разработке программы, осуществляющей прогноз уровней подземных вод с использованием нейросетевых технологий и с помощью статистических методов прогнозирования.
|
Задачи работы
1. Сбор гидрогеологических данных по уровню подземных вод в Донецкой области, на основе информации Минтопэнерго Украины.
2. Классификация данных уровня подземных вод по однородным классам и создание базы данных на основе полученной информации.
3. Системный и структурный анализ данных и установление закономерностей изменения уровней подземных вод в рамках однородных классов.
4. Разработка зависимостей для прогноза и оценки уровня подземных вод.
5. Разработка информационно аналитической системы на базе нейросетевых моделей для анализа и оценки уровня подземных вод.
|
Методы исследований
При выполнении работы предполагается использовать методы системного и структурного анализа данных, статистические методы – корреляционный и регрессионный анализ, статистический анализ распределения данных, стохастические методы анализа временных рядов – метод авторегрессии проинтегрированного скользящего среднего, имитационное моделирование распределений, методы нейросетевых технологий, разработка объектных компьютерных моделей для оценки уровня подземных вод.
При выполнении работы предполагается использование следующих инструментальных средств:
- систем STATISTICA – для анализа данных и создания нейросетевой модели;
- языка проектирования баз данных MySQL – для создания базы данных опасных событий и чрезвычайных ситуаций;
- языка программирования Borland C++ Builder – для создания объектных модулей информационно – аналитической системы;
- систем объектного моделирования для создания компьютерных моделей.
Информационной основой исследования являются базы данных по уровням подземных вод, которые отслеживаются в течении длительного периода различными организациями Донецкой области.
|
Анализ временных рядов и прогнозирование (программный пакет STATISTICA)
Пакет STATISTICA фирмы StatSoft является интегрированной системой комплексного статистического анализа и обработки данных в среде Windows и занимает устойчивое лидирующее положение на рынке статистического программного обеспечения.
Модуль временные ряды. В данном модуле реализован широкий набор методов описания, построения моделей, декомпозиции и прогнозирования временных рядов как во временной, так и в частотной области. Все процедуры полностью интегрированы и результаты анализа одной модели (например, остатки, вычисленые для модели АРПСС) можно использовать для дальнейшего анализа (например, вычисления автокорреляции остатков). Имеются самые разнообразные возможности для просмотра и графического представления одномерных и многомерных рядов. Можно анализировать очень длинные ряды (более 100 тыс. наблюдений для компьютера с 8 Mb оперативной памяти). С многомерными рядами (в случае многомерных исходных данных или с рядами, полученными на различных этапах анализа) можно работать в активной рабочей области; здесь их можно просматривать и сопоставлять друг с другом. [4]
Модуль Временные ряды включает полную реализацию модели авторегрессии и проинтегрированного скользяцего среднего (АРПСС).
В системе STATISTICA реализованы регрессионные методы анализа временных рядов для переменных с запаздыванием (лагом) или без него, в том числе - регрессия, проходящая через начало координат, нелинейная регрессия и интерактивное "что-если" прогнозирование.
Модуль STATISTICA Neural Networks
В модуле Neural Networks реализованы следующие топологии нейронных сетей:
MLP (MultiPlayer Perceptron) – многослойный персептрон;
RBF (Radical Basis Function) – радиальные базисные функции;
PNN – вероятностная нейронная сеть;
GRNN – обобщенно-регрессионная нейронная сеть.
Linear – линейная;
Kohonen – сеть Кохонена.
Каждая из топологий имеет свои достоинства и недостатки и может использоваться для различного класса задач. Помимо топологии, сеть характеризуется количеством промежуточных слоев, количеством входных и выходных переменных, типом передаточной функции и др.
|
Метод авторегрессии и проинтегрированного скользящего среднего
(ARIMA – АРПСС)
Большое количество экологических и социально-экономических процессов описываются моделями АРПСС. Метод АРПСС основан на использовании процессов авторегрессии и скользящего среднего.
Процесс авторегрессии. Большинство временных рядов содержат элементы, которые последовательно зависят друг от друга. Такую зависимость можно выразить следующим уравнением:
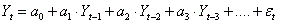 , ,
где 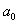 - свободный член; - свободный член;
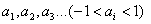 - параметры авторегрессии. - параметры авторегрессии.
Видно, что для этой модели каждое наблюдение есть сумма случайной компоненты (случайное воздействие ) и линейной комбинации предыдущих наблюдений.
Процесс скользящего среднего. В отличие от процесса авторегрессии, в процессе скользящего среднего каждый элемент ряда подвержен суммарному воздействию предыдущих ошибок.
В общем виде уравнение прогноза можно записать следующим образом:
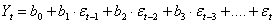 , ,
Другими словами, текущее наблюдение ряда представляет собой сумму случайной компоненты (случайное воздействие ) в данный момент времени и линейной комбинации случайных воздействий в предыдущие моменты времени.
Модель авторегрессии и скользящего среднего. Общая модель, предложенная Боксом и Дженкинсом (1976) может включать как параметры авторегрессии, так и параметры скользящего среднего. Имеется три типа параметров модели: параметры авторегрессии (p), порядок разности (d), параметры скользящего среднего (q). В обозначениях Бокса и Дженкинса модель записывается как АРПСС (p, d, q).
В общем виде данная модель может быть записана следующим образом:
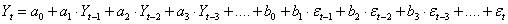 . .
Оценивание и прогноз.
Следующий после идентификации шаг – оценивание. Он состоит в оценивании параметров модели.
Полученные оценки параметров используются на последнем этапе – выполнении прогноза. На этом этапе вычисляются новые значения ряда, и строится доверительный интервал прогноза. Процесс оценивания проводится по преобразованным данным. Оценка значимости параметров основывается на использовании t-статистики. Если значения вычисляемой t-статистики не значимы, соответствующие параметры в большинстве случаев удаляются из модели без ущерба подгонки, а модель пересчитывается. [5]
|
Применение нейросетевых технологий
В данном разделе рассматриваются искусственные нейронные сети, их применение при решении задач прогнозирования временных рядов, в частности изменения уровня подземных вод.
Искусственные нейронные сети получили широкое распространение за последние 20 лет и позволили решать сложные задачи обработки данных, часто значительно превосходя точность других методов статистики и искусственного интеллекта, либо являясь единственно возможным методом решения отдельных задач. [6]
После изучения топологий нейронных сетей, анализа достоинств и недостатков каждой, была выбрана архитектура многослойного персептрона для конкретной задачи прогнозирования.
Многослойный персептрон (MLP) представляет собой архитектуру сети, которая используется сейчас наиболее часто. Эта сеть является наиболее универсальной и может использоваться для решения разнообразных задач, однако преимущество отдается задачам классификации, прогнозирования, и распознавания. Архитектура сети была предложена в работе Rumelhart, McClelland (1986) и подробно обсуждается почти во всех учебниках по нейронным сетям. Каждый элемент сети строит взвешенную сумму своих входов с поправкой в виде слагаемого и затем пропускает эту величину активации через передаточную функцию, и таким образом получается выходное значение этого элемента. Элементы организованы в послойную топологию с прямой передачей сигнала (рис. 1).

Рисунок 1 – Архитектура сети многослойного персептрона (Анимация)
Такую сеть легко можно интерпретировать как модель вход-выход, в которой веса и пороговые значения (смещения) являются свободными параметрами модели. Такая сеть может моделировать функцию практически любой степени сложности, причем число слоев и число элементов в каждом слое определяют сложность функции. Определение числа промежуточных слоев и числа элементов в них является важным вопросом при конструировании.
Количество входных и выходных элементов определяется условиями задачи.
При построении сети задача подачи входных сигналов и снятие выходных сигналов сети была решена следующим образом. На веса синапсов сети обычно налогаются требования принадлежности некоторому диапазону значений, например [0,1]. Наиболее часто используемые нелинейные функции нейронов также обычно выдают значения из некоторого диапазона. Это приводит к тому, что обычно нельзя подавать сети входные сигналы в их истинном диапазоне величин и получать от сети выходные сигналы в требуемом диапазоне.
Поэтому перед подачей входных сигналов данные были пронормированы следующим образом.
Каждая компонента входного вектора данных xi заменяется величиной
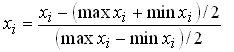
где max xi и min xi – соответственно максимальное и минимальное значения для данной компоненты, вычисленные по всей обучающей выборке. По этой же формуле пересчитываются и компоненты векторов ответов [1].
Следующий этап – обучение нейронной сети. Обучение может быть с учителем или без него. Для обучения с учителем нужен «внешний» учитель, который оценивал бы поведение системы и управлял ее последующими модификациями. Обучение персептрона является обучением с учителем.
Персептрон обучают, подавая множество образов по одному на его вход и подстраивая веса до тех пор, пока для всех образов не будет достигнут требуемый выход.
Пусть X – образ распознаваемой цифры.
Каждая компонента x=(x1,x2,…,xn) умножается на компоненту вектора весов A: G=XA.
Если сумма произведений превышает порог, то выход нейрона Y равен 1, иначе 0.
Для обучения сети образ X подается на вход и вычисляет выход Y используя случайные значения весов aij. Если Y правильный, то ничего не меняем, иначе веса корректируются.
Если в результате обучения выход неправилен, то веса, присоединенные к входам, усиливающим ошибочный результат, модифицируется, чтобы уменьшить ошибку.
Метод обучения представлен следующей блок-схемой.
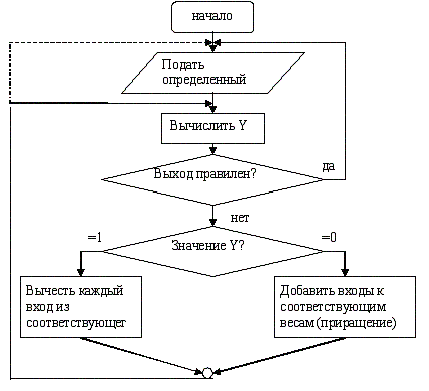
Рисунок 2- Алгоритм обучения
За конечное число шагов сеть научится относить значения к разным диапазонам. Необходимо отметить, что это обучение глобально, т. е. сеть обучается на всем множестве значений [3].
Данный алгоритм необходимо дополнить внешним циклом который будет продолжать (повторять) обучение на всем множестве до тех пор пока все цифры одновременно не будут распознаваться правильно.
После построения и обучения нейросети можно судить о качестве: чем меньше значение ошибки, тем лучше качество сети. В нашем случае ошибка сети, полученная на контрольном подмножестве, которая вычисляется по всем контрольным наблюдениям = 1.719e-06. Но оценивая первые опыты моделирования, не следует особенно доверять полученным результатам, поскольку в прогнозе не учитываются многие косвенные взаимодействия в подземном слое и процессы, проходящие в атмосфере. Следующим этапом работы будет оценивание точности прогнозирования известных данных при помощи нейросетевых методов обработки информации.
|
Заключение
Текущие и планируемые результаты по теме (на этапе курсовго проєктирования):
изучение литературных источников и нормативных документов по вопросам гидрогеологической обстановке на территории Донецкой области;
анализ существующих методов прогноза и оценки уровня подземных вод, классификация и идентификация данных;
сбор данных по гидрогеологической обстановке и подготовка файлов собранной информации;
создание базы данных по уровню подземных вод и системы запросов для подготовки данных к последующему анализу;
разработка плана, выбор методов и формулировка содержания работ будущей магистерской работы.
Курсовой проект по теме магистерской работы является первой стадией на этапе подготовки магистра, и его результаты будут использованы в будущей работе над магистерской диссертацией.
При написании данного автореферата магистерская работа еще не завершена. Окончательное завершение: январь 2007 года. Полный текст работы и все материалы по теме могут быть получены у автора или его руководителя после указанной даты.
|
Список источников
1. Лбов Г.С. Методы обработки разнотипных экспериментальных данных. – Новосибирск: Наука, 1981. – 157с.
2. Методы нейроинформатики / Под. ред. А.Н. Горбаня; отв. за выпуск М.Г. Доррер. КГТУ, Красноярск, 1998. 205 с.
3. Ф. Уоссермен. Нейрокомпьютерная техника: теория и практика. Русский перевод: Ю. А. Зуев, В. А. Точенов, – М: Мир. – 1992.
4. Временные ряды Сайт http://www.statsoft.ru/home/products/Statistica/details/sta_tim/default.htm 10.05.2006
5. Боровиков В. STATISTICA для профессионалов. СПб.: Питер. 2001. – 655с.
6. NeyroPro Сайт http://www.neuropro.ru/soft.shtml 18.04.2005
|
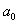 - свободный член;
- свободный член;
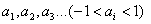 - параметры авторегрессии.
- параметры авторегрессии.