Чвала Алексей Алексеевич

Актуальность работы

Исследование принципов, лежащих в основе строения и функционирования системы кровообращения, является чрезвычайно актуальной научной проблемой. Это обусловлено не только сложностью фундаментальных аспектов, но и практическим интересом, связанным с широкой распространенностью сосудистых заболеваний, ведущих к гемоциркуляторным расстройствам и серьезным нарушениям со стороны внутренних органов. Высокая частота встречаемости и особая тяжесть сосудистыx заболеваний требуют усовершенствования знаний в этой области и разработки новых, эффективных способов их диагностики и лечения, а также прогнозирования результатов хирургической коррекции гемодинамических растройств. Отсутствие в настоящее время количественных критериев нормы строения артериального русла существенно сдерживает развитие этого перспективного направления клинической медицины. Cуществующие способы оперативного лечения артериальных стенозов (наиболее частой причины гемоциркуляторных расстройств) сводятся к реконструкции русла путем формирования новых обходных путей или механическому расширению суженных участков – баллонной ангиопластике (БА). В настоящий момент успех процедуры БА во многом случаен, т.к. отсутствуют методы объективного контроля за поведением артерии при больших деформациях и разрушении. Имеет место недостаток сведений о ее биомеханических свойствах, в частности упругости.

Обзор существующих исследований

Недостаточно изученными остаются упругие свойства артерий различного типа. Это связано с тем, что в процессе биомеханических испытаний артерия ведет себя вначале как упругое или вязко-упругое тело, а с определенного момента реагирует на деформацию как пластическое или вязко-пластическое. Методов исследования упругого и пластического компонентов в настоящее время не существует. Решение задачи определения гемодинамического сопротивления артериального русла связано с преодолением больших трудностей. Для этого необходимо знать геометрию и топологию, а также упругие характеристики каждого звена артериального дерева человека. В отечественной и зарубежной литературе имеются лишь фрагментарные данные о некоторых количественных параметрах отдельных участков артериального русла большого круга кровообращения, что связано с особыми трудностями регистрации длины, диаметра и топологических характеристик артерий мелкого диаметра, особенно интраорганных. Оптимальным способом решения данного вопроса является математическое моделирование деления артерий до уровня микроциркуляторного русла. При этом необходимо учитывать общие и специфические морфо-функциональные закономерности, лежащие в основе организации артериальных деревьев различных органов.

Решаемые в работе задачи

Основная решаемая задача - создание специализированной компьютерной системы для моделирования гемодинамической структуры артериального русла человека, основанную на морфометрических данных об экстраорганной части артериального русла. Использование созданной модели гемодинамики в условиях эксперимента на компьютере даст возможность получения новых сведений о различных аспектах гемоциркуляции.

Теоретический анализ

Генетические алгоритмы предназначены для решения задач оптимизации. Применение нейросетевого метода в связке с генетическим алгоритмом, использующемся как средство нахождения весов для нейронов сети, позволит провести полное моделирование гемодинамической структуры артериального русла человека с учетом специфических особенностей строения сосудов каждого органа. Генетические Алгоритмы - адаптивные методы поиска, которые в последнее время часто используются для решения задач функциональной оптимизации. Они основаны на генетических процессах биологических организмов: биологические популяции развиваются в течении нескольких поколений, подчиняясь законам естественного отбора и по принципу "выживает наиболее приспособленный" (survival of the fittest), открытому Чарльзом Дарвином. Подражая этому процессу генетические алгоритмы способны "развивать" решения реальных задач, если те соответствующим образом закодированы. Например, ГА могут использоваться, чтобы проектировать структуры моста, для поиска максимального отношения прочности/веса, или определять наименее расточительное размещение для нарезки форм из ткани. Они могут также использоваться для интерактивного управления процессом, например на химическом заводе, или балансировании загрузки на многопроцессорном компьютере. Вполне реальный пример: израильская компания Schema разработала программный продукт Channeling для оптимизации работы сотовой связи путем выбора оптимальной частоты, на которой будет вестись разговор. В основе этого программного продукта и используются генетические алгоритмы. Основные принципы ГА были сформулированы Голландом (Holland, 1975), и хорошо описаны во многих работах. В отличии от эволюции, происходящей в природе, ГА только моделируют те процессы в популяциях, которые являются существенными для развития. Точный ответ на вопрос: какие биологические процессы существенны для развития, и какие нет? - все еще открыт для исследователей. В природе особи в популяции конкурируют друг с другом за различные ресурсы, такие, например, как пища или вода. Кроме того, члены популяции одного вида часто конкурируют за привлечение брачного партнера. Те особи, которые наиболее приспособлены к окружающим условиям, будут иметь относительно больше шансов воспроизвести потомков. Слабо приспособленные особи либо совсем не произведут потомства, либо их потомство будет очень немногочисленным. Это означает, что гены от высоко адаптированных или приспособленных особей будут распространятся в увеличивающемся количестве потомков на каждом последующем поколении. Комбинация хороших характеристик от различных родителей иногда может приводить к появлению "суперприспособленного" потомка, чья приспособленность больше, чем приспособленность любого из его родителя. Таким образом, вид развивается, лучше и лучше приспосабливаясь к среде обитания. ГА используют прямую аналогию с таким механизмом. Они работают с совокупностью "особей" - популяцией, каждая из которых представляет возможное решение данной проблемы. Каждая особь оценивается мерой ее "приспособленности" согласно тому, насколько "хорошо" соответствующее ей решение задачи. Например, мерой приспособленности могло бы быть отношение силы/веса для данного проекта моста. (В природе это эквивалентно оценке того, насколько эффективен организм при конкуренции за ресурсы.) Наиболее приспособленные особи получают возможность "воспроизводит" потомство с помощью "перекрестного скрещивания" с другими особями популяции. Это приводит к появлению новых особей, которые сочетают в себе некоторые характеристики, наследуемые ими от родителей. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков, так что те свойства, которыми они обладали, будут постепенно исчезать из популяции в процессе эволюции. Так и воспроизводится вся новая популяция допустимых решений, выбирая лучших представителей предыдущего поколения, скрещивая их и получая множество новых особей. Это новое поколение содержит более высокое соотношение характеристик, которыми обладают хорошие члены предыдущего поколения. Таким образом, из поколения в поколение, хорошие характеристики распространяются по всей популяции. Скрещивание наиболее приспособленных особей приводит к тому, что исследуются наиболее перспективные участки пространства поиска. В конечном итоге, популяция будет сходиться к оптимальному решению задачи. В настоящее время под термином "генетические алгоритмы" скрывается не одна модель, а достаточно широкий класс алгоритмов, подчас мало похожих друг от друга. Исследователи экспериментировали с различными типами представлений, операторов кроссовера и мутации, специальных операторов, и различных подходов к воспроизводству и отбору. Хотя модель эволюционного развития, применяемая в ГА, сильно упрощена по сравнению со своим природным аналогом, тем не менее ГА является достаточно мощным средством и может с успехом применяться для широкого класса прикладных задач, включая те, которые трудно, а иногда и вовсе невозможно, решить другими методам. Однако, ГА, как и другие методы эволюционных вычислений, не гарантирует обнаружения глобального решения за полиномиальное время. ГА-мы не гарантируют и того, что глобальное решение будет найдено, но они хороши для поиска "достаточно хорошего" решения задачи "достаточно быстро". Там, где задача может быть решена специальными методам, почти всегда такие методы будут эффективнее ГА и в быстродействии и в точность найденных решений. Главным же преимуществом ГА-мов является то, что они могут применяться даже на сложных задачах, там, где не существует никаких специальных методов. Даже там, где хорошо работаю существующие методики, можно достигнуть улучшения сочетанием их с ГА.

Экспериментальные исследования

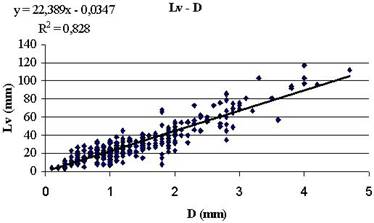
На основе фактического материала, накопленного сотрудниками кафедры анатомии человека Донецкого медицинского университета, были проведены исследования кровеносной системы с учетом особенностей топологии для каждого органа человека. Вся модель кровеносного русла имеет древообразную структуру (циклическая структура сосудов присутствует только в тканях кишечника). В древообразной модели каждый сосуд может быть материнским только для двух сосудов, т.е. из одного сосуда выходит только два сосуда неравных диаметров. Для построения модели необходимы зависимости диаметра большего исходящего сосуда от диаметра материнского сосуда, зависимость диаметра меньшего исходящего сосуда от диаметра материнского сосуда и зависимость длины всей ветви от диаметра материнского сосуда, которые были получены с помощью регрессионного анализа (рис.1).

Рисунок 1 – Зависимость длины кровеносной ветви от внутреннего диаметра материнской артерии почки

Алгоритм получения диаметров сосудов всей модели можно представить в виде последовательности шагов:
1. рассчитываются два исходящих из материнской артерии сосуда
2. каждый из них принимается за материнскую артерию
3. для каждого из полученных сосудов повторяется действие 1
Этот процесс продолжается до тех пор, пока диаметры рассчитываемых сосудов не станут меньше заданного предела. Достаточным пределом точности, необходимым для решения практических задач, является величина диаметра сосудов до 0.1 мм (уровень капилляров). Для определения длин рассчитываемых сосудов древообразная модель рассматривается как единое целое, а не как независимые друг от друга участки. Модель рассматривается в обратном порядке (от уровня капилляров к материнской артерии). Для каждого органа в организме человека действуют свои законы расположения сосудов, поэтому при моделировании кровеносного русла учитываются особенности морфологической структуры каждого органа. Для сосудов почки функции для создания модели имеют вид (1). Для остальных органов получены аналогичные функции.

(1)

где Dmax(D) - зависимость диаметра большего исходящего сосуда от диаметра материнского сосуда, Dmin(D) - зависимость диаметра меньшего исходящего сосуда от диаметра материнского сосуда, Lv(D) – зависимость длины всей ветви от диаметра материнского сосуда. Для оценки сопротивления отдельных кровеносных сосудов используется формула Пуазейля:

(2)

где: R - гидродинамическое сопротивление, eta - вязкость крови, L - длина сосуда, D – внутренний диаметр сосуда, 128 и pi – константы. Для расчета объемной скорости тока и давления в них необходимо учитывать характер соединения сосудов (последовательный или параллельный) [3]. При последовательном соединении сосудов сопротивление их складываются:

(3)

а при параллельном соединении складываются обратные величины сопротивлений:

(4)

Сопротивление внутриорганных сосудов вплоть до уровня деления капилляров находилось и использованием данных модели деления сосудов, описанной выше. Кроме древовидной структуры в организме человека в тканях кишечника встречается циклическая модель кровеносного русла. Построение модели для такого типа сосудов отличается от древовидной модели, но любая циклическая модель заканчивается разветвленной сетью древовидных сосудов. Обычно внутренний диаметр циклических сосудов не больше 0.7 мм. При меньшем диаметре циклическая структура переходит в древовидную.

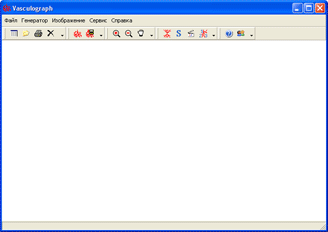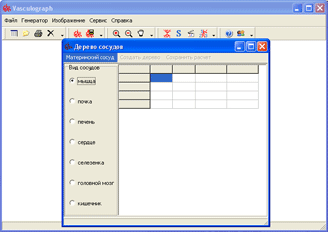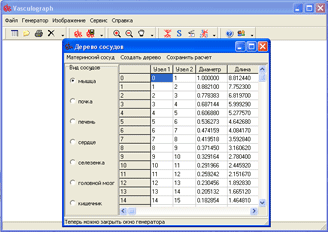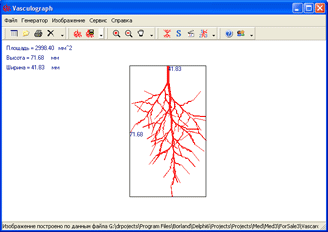
Рисунок 2 – Программа Vasculograph

Результатом этих исследований стала разработка программы Vasculograph (рис.2). Она позволяет строить планарное изображение кровеносного русла основанное на данных полученных экспериментальным путём из коррозионных препаратов органов человека или полученных по определённым математическим зависимостям. Программа может определять геометрические параметры кровеносного русла такие как длину, ширину и площадь лоскута-той части ткани которую кровоснабжает данный участок кровеносного русла, указанные геометрические параметры являются очень важными в пластической хирургии и разнообразных исследованиях связанных с гемодинамикой и принципами формирования кровеносного русла.

Обзор результатов и выводы

Используемые в настоящее время оперативные методы коррекции патологически измененного артериального русла не всегда дают желаемые результаты. Это обусловлено тем, что в артериальном русле, при известных приближениях действуют законы, аналогичные законам в электрической цепи и изменение сопротивления одного участка неизбежно приводит к изменению тока не только в этом участке, но и в системе в целом. Поэтому в условиях множественного поражения сосудов, что почти всегда наблюдается при атеросклерозе, врач не может достаточно точно предсказать, какие изменения кровообращения произойдут при том или ином оперативном пособии, а значит, не может выбрать оптимальный вариант операции для каждого конкретного больного. В будущем в клинических условиях практическое применение модели гемодинамики даст возможность объективного планирования мероприятий по реконструкции патологически измененного артериального русла. Использование программного комплекса при проведении БА поможет снизить вероятность внутриоперационных и ранних послеоперационных осложнений.

Литература

1. Зенин О.К., Гусак В.К., Кирьякулов Г.С. и др. Артериальная система человека в цифрах и формулах.-Донецк.- 2002.-196с.
2. Кизилова Н. Н. Отражение пульсовых волн и резонансные свойства артериальных русел с анастомозами // Мат. моделирование. – 2003
3. Olufsen, M. S. Modeling the Arterial System with Reference to an Anesthesia Simulator. Technical report, IMFUFA Text 345,1998. Roskilde University, Denmark, Ph.D. Thesis.
4. Zamir, M., Shee, H.: Branchimg characteristics of human coronary arteries. Canad.J. Physiol. Pharmacol. 64 (1996) 661-668
5. Vito R.P., Dixon S.A. Blood vessel constitutive models - 1995-2002 // Ann. Rev. Biomed. Eng. – 2003. – Vol. 5, № 4.
6. Cirovic S., Walsh C., Fraser W.D. Mathematical study of the role of non-linear venous compliance in the cranial volume-pressure test // Med. Biol. Eng. Comput. – 2003.
7. http://www.basegroup.ru
8. http://www.neuroproject.ru
9. Grodins F.S. Integrative cardiovascular physiology: A mathematical synthesis of cardiac and blood vessel hemodynamics //Quart.Rev.Biol.-1959.-Vol.34.-P.93-116.

Примечание: Данный автореферат не является окончательной версией магистерской работы. Полная версия предположительно будет готова в декабре 2006. За полной версией обращайтесь к автору.