Реферат

Дослідження електропровідних властивостей викопного вугілля в процесі коксування

Читати англомовний варіант(ENG)>>

Ситуація, що складається в світі в енергетичній галузі та галузі видобутку корисних копалин, примушує більш уважно ставитися до тих природних ресурсів, кількість яких поступово зменшується, а видобуток с кожним роком дорожчає.

Кількість запасів вугілля у світі ще доволі велика і достатня для того, щоб забезпечувати людство протягом багатьох десятиліть, на відміну від нафти та природного газу, нестача яких вже відчувається. Але ці запаси розкидані по всьому світові досить нерівномірно і характеризуються різними властивостями. Особливо це актуально для України, на шахтах якої видобувається вугілля з значним вмістом сірки та невисокою здатністю до спікливості.

Тому для виготовлення високоякісного коксу до свого вугілля доводиться додавати більш якісне російське, або взагалі переходити на привізне. В часи існування Радянського Союзу ця проблема не була такою актуальною – вугілля вистачало на всіх.

Натомість, вимоги, які металургійні підприємства пред’являють до якості коксу, навпаки постійно зростають, оскільки такого коксу треба менше, а метал при цьому отримується чистіший.

Один з шляхів до зменшення витрат і отримання коксу задовільної якості – підбирання оптимального складу шихти. Для цього можна використовувати різні методи, але всі вони зводяться до постійних перерахунків матеріального і теплового балансу.

Вивчення електропровідних та теплофізичних властивостей може допомогти під час розрахунку складу шихти і прогнозування якості коксу.

Мета роботи – експериментально вивчити теплофізичні та електричні процеси, що мають місце під час піролізу вугілля; розробити лабораторну установку для вимірювання електропровідності вугільного завантаження з одночасним його нагріванням; створити математичну модель розподілу температури в лабораторній установці, враховуючи залежність теплофізичних параметрів вугілля від температури.

Вивчення електричних властивостей вугілля та коксу проводилися і раніше - достатньо почитати наявну на сайті бібліотеку.

Визначення електричних параметрів кам'яного вугілля пов'язано з рядом труднощів методологічного характеру, в числі яких підготовка вугільних зразків до дослідження. Виготовлення зразків з цільних блоків вугілля є трудомісткою операцією, а вимірювання з їх використанням не виключають можливості спотворення одержуваних результатів через наявність в зразках чужорідних включень.

Ще складніше виконати вимірювання чисельних значень електричних параметрів вугілля в процесі їх нагрівання, що супроводиться виділенням летючих продуктів деструкції, переходом речовин вугілля пластичний стан, утворенням пор, тріщин і усадкою коксу. Це не дозволяє використовувати відомі методи, засновані на прямому контакті вимірювальних елементів з вугіллям, що нагрівається. Тому, наприклад, дослідження впливу теплової дії на електричний опір вугілля проводять, як правило, з використанням зразків, виготовлених із заздалегідь нагрітих і потім охолоджених проб вугілля. Охолоджування вугілля знижує інтенсивність внутрішньомолекулярних коливань і приводить до зміни електрофізичних властивостей, які характерні для вугілля в нагрітому стані. Саме ці характеристики, як і відмінність їх від властивостей охолоджених продуктів, мають велике значення для пізнання структурних перетворень речовин вугілля [16].

Таблиця 1 – Рівень змін електричних властивостей в залежності від температури.

Температура, °С	100	200	300	400	500	600	700	800
Рівень "фону", мВ	0.100	0.125	0.200	0.340	0.560	1.000	1.280	1.450

Відмічені відхилення показань приладу враховували при обробці результатів вимірювань комплексної провідності вугілля [16].

Для вирішення задачі знаходження розподілу температури шириною завантаження був використаний відомий пакет для кінцево-елементного аналізу ANSYS. Комплекс ANSYS дозволяє інженерам-дослідникам вирішувати задачі розрахунку розподілу температурних полів, динаміки рідини і газу, електромагнітних і акустичних полів і багато інших. Метод кінцевих елементів є чисельним методом, що використовується для отримання рішень великого класу інженерних завдань, включаючи розрахунок конструкцій на міцність, розрахунок розповсюдження тепла, електромагнетизм і гідромеханіку.

Паралельно ідентичні розрахунки проводилися з використанням російського пакету ELCUT. За допомогою цього пакету можна розрахувати розподіл температур для установки з будь-якими геометричними та іншими характеристиками.

Збір та первинна обробка даних виконувалася за допомогою ЕОМ.

Проведення лабораторного експерименту можна розбити на наступні етапи:

- підготовка вугілля до експерименту, а саме: подрібнення його до заданої крупної 0.25 мм і обезводнення в сушильній шафі до постійності ваги;

- зволоження вугільного навішування масою 40 г до заданої умовою вологості додаванням води і перемішування для рівномірного розподілу вологи за всім обсягом;

- зачистка внутрішнього і зовнішнього стаканів осередку для поліпшення електричного контакту на межі розділу фаз;

- підготовка азбестової прокладки всередину зовнішнього стакана щоб уникнути безпосереднього контакту між електродами на дні;

- завантаження в осередок заздалегідь підготовленого вугільного навішування;

- ущільнення навішування за всім обсягом в осередку до заданої щільності завантаження;

- занурення осередку в нагрівальну піч точно у її центр;

- занурення термопари у вугільне завантаження і підключення її до АЦП;

- підключення осередку двома клемами до АЦП;

- включення печі в мережу і завдання швидкості нагріву вугільного завантаження за допомогою регулювання напруги, що подається на піч автотрансформатором;

- запуск програмного забезпечення експерименту;

- закінчення експерименту по досягненню температури 700° С;

- відключення живлення печі і зупинка програмного забезпечення;

- збереження даних експерименту в текстовому форматі;

- обробка результатів експерименту.

На початковому етапы розробки методики дослідження проводилися на інертному матеріалі – піску, а також на антрациті, який не переходить в пластичний стан.

 У пісок додавалася вода до 10% від його маси. Відомо, що пісок не володіє провідністю, тому всі зміни електричних ефектів в даному випадку можуть бути віднесені до води. Зміна провідності піску від температури представлені на рис. 3.4.

Як видно, провідність води дуже висока, прилад зафіксував максимальне значення напруги 5.12 В. Прі нагріві до 207°C провідність практично не змінюється; після досягнення температури 207°C починається різкий спад провідності і при температурі 250°C ми спостерігаємо повну відсутність провідності. Отже в завантаженні залишився виключно пісок. Відомо, що процес випаровування вологи починається при 100°C і може продовжуватися до 250°C, отже волога, що випарувалася до 207°C не впливає на процес провідності, а та що випарувалася інтервалі температур  207-250°C грає основну роль в провідності піску.

Рисунок 1 – Зміна провідності вологого піску від температури

На наступному етапі були проведені дослідження провідності антрациту і термічно підготовленого антрациту (а саме того ж самого антрациту, на якому проводився експеримент в першому випадку). Початковий антрацит показав на початку провідність 2.96 В, але вона почала знижуватися до 2.66 при 700°C. Після цієї точки починається зростання провідність і при 160°C досягається значення 3.57 В і воно не змінюється до 185°C після чого знову починається зростання провідності і максимум її досягається при 335 °C і складає 4.75 В. Ця напруга не змінюється до кінця процесу.

Після закінчення експерименту антрацит розсипався рівномірно на сухій поверхні і піддавався природній сушці. Відомо, що термічно підготовлений антрацит використовується як адсорбент. Ефект зміни провідності у зв'язку з накопиченням вологи і газів розвиненою поверхнею вугілля і хотілося поспостерігати.
При початковій температурі термоантрацит показав значення провідності нижче ніж в першому випадку – тільки 2.67 В, але надалі спостерігалося її зростання до 4.35 при 70°C (у першому випадку при цій температурі ми мали мінімум) і почалося падіння провідності і з'явився мінімум при 153 °C рівний 3.21 В. Після цього провідність починає рости і досягається граничне значення 4.75 В при 350°C і до кінця експерименту не змінюється.

Як ми бачимо в результаті термоантрацит виходить на те ж значення провідності, що і антрацит – 4.75 В практично при такій же температурі.

Рисунок 2 – Зміна провідності антрациту і термоантрациту від температури

 

Наступним етапом було проведення експериментів на вугіллі марки Ж, оскільки він переходить в пластичну масу. Зміну провідності вугілля Ж від температури нагрівання представлено на рис. 3.

Досліджувалися дві паралельні проби вугілля. При 20 °C для обох проб спостерігалося однакове значення провідності 4.73 В. Під час нагрівання провідність трохи збільшувалася до 4.74 В для першої проби і 4.86 В – для другої. Різке падіння її спостерігалося починаючи з 45 °C і з 60 °C у першому і другому випадку відповідно і продовжувалося до 105°C у обох випадках до значення 0.28 В. До 135 °C змін не спостерігалося, а після різко падає напруга до 0.07 В. Це значення практично не змінюється до 400 °C і починає рости. У першому випадку провідність досягає максимального значення в 4.76 В при 570 °C, а в другому – при 620 °C.    

Рисунок 3 - Зміна провідності двох проб вугілля Ж від температури

 Всі експериментальні дані зведені на рис. 4

Рисунок 4 – Зведений графік

 

Використання програмного пакету ELCUT 5.3

ELCUT – інтегрована діалогова система програм, яка дозволяє вирішувати двовимірні та вісесиметричні задачі. Пакет дозволяє проводити розрахунок і моделювання полів методами кінцевих елементів.

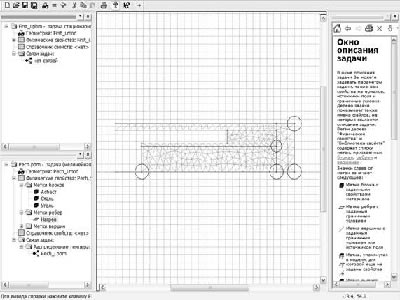
Рисунок 5 – Зовнішній вигляд інтерфейсу ELCUT

Впровадження у виробництво складної техніки приводить до необхідності створення систем автоматизованого проектування, оскільки багато практично важливих технічних задач не можуть бути вирішені аналітично в наслідок складності геометрії конструкції і граничних умов. Тому для того, щоб врахувати реальні особливості досліджуваного матеріалу, доводиться вдаватися до чисельних методів розрахунку. На відміну від аналітичного рішення, яке описує поведінку системи в будь-якій точці, чисельне рішення апроксимує точне рішення тільки в дискретних точках. Першим кроком при отриманні чисельного рішення є побудова дискретної моделі безперервної величини. Широко застосовуються два основні чисельні методи – метод кінцевих різниць і метод кінцевих елементів. У методі кінцевих різниць диференціальні рівняння, що описують фізичний процес, що відбувається, записуються для кожного вузла і частинні похідні за часом замінюються їх кінечно-різницевим аналогом із застосуванням центральної різницевої схеми. Кінечно-різницевий метод дуже ефективний при рішенні простих задач, але його складно застосовувати при розв’язанні задач зі складною геометрією, не лінійними властивостями матеріалу конструкції або з складними граничними умовами.

Область застосування методу кінцевих елементів охоплює практично всі фізичні задачі, які можуть бути описані диференціальними рівняннями. Основна ідея методу кінцевих елементів полягає в тому, що будь-яку величину можна апроксимувати дискретною моделлю, яка будується на безлічі шматково-безперервних функцій, визначених на кінцевому числі підобластей (елементів). Важливою є можливість виділити з набору елементів типовий елемент і знайти безперервну функцію, що представляє наближене рішення для цього елементу безвідносно від положення цього елементу в загальній зв'язній моделі і від функцій інших елементів, а потім отримати загальне рішення для всієї моделі, компонуючи ці частинні рішення, використовуючи при цьому безперервність функцій на межах елементів і граничні умови.

Метод кінцевих елементів є чисельним методом, що використовується для отримання рішень великого класу інженерних завдань, включаючи розрахунок конструкцій на міцність, розрахунок розповсюдження тепла, електромагнетизм і гідромеханіку.

Температурний аналіз відіграє помітну роль при проектуванні багатьох механічних і електромагнітних систем. Як правило, інтерес складають розподіл температури, температурного градієнта й теплового потоку. Вирішуючи нестаціонарну теплову задачу, можна  проаналізувати зміну температури в часі.

ELCUT може виконувати лінійний і нелінійний температурний аналіз у плоскій і вісесиметричній постановці. Формулювання завдання ґрунтується на рівнянні теплопровідності із граничними умовами радіаційного й конвективного теплообміну.

ELCUT дозволяє вирішувати задачі теплопередачі в лінійній і нелінійній постановках. При вирішенні теплових задач використовується рівняння теплопровідності в одному з видів:
Для лінійних задач:

	- у плоскому випадку;
	- в вісесиметричному випадку;

Для нелінійних задач:

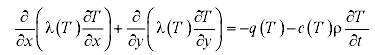	- у плоскому випадку;
	- в вісесиметричному випадку;

де:
T - температура;
 t - час;
 λx(y,r,z) - компоненти тензора теплопровідності (у лінійній постановці);
λ(T) - теплопровідність як функція температури, представлена кубічним сплайном (анізотропія не підтримується в нелінійній постановці);
 q(T) - питома потужність тепловиділення; у лінійній постановці - константа, у нелінійній постановці - задається_ кубічним сплайном функція температури;
 c(T) - питома теплоємність, у нелінійному випадку це функція температури, апроксимована кубічними сплайнами;
ρ - щільність.
Всі параметри рівнянь у лінійній постановці постійні в межах кожного блоку моделі.
При постановці завдання можна використовувати наступні можливості:

• Властивості середовищ: ортотропні матеріали з постійною теплопровідністю, ізотропні матеріали з теплопровідністю й теплоємністю, які залежать від температури.
• Джерела поля: постійні й залежні від температури об'ємні джерела теплової потужності, конвективні й радіаційні джерела, імпортована із завдання розтікання струмів.
• Граничні умови: задана температура, заданий тепловий потік на границі, умови радіаційного й конвективного теплообміну а також поверхні з постійної, наперед невідомою температурою.
• Результати розрахунку: температура, градієнт температури, щільність теплового потоку й інтегральні значення теплового потоку через задані поверхні. Для нестаціонарної задачі: графіки й таблиці зміни фізичної величини в часі.
• Спеціальні можливості: Інтегральний калькулятор може обчислювати різні інтегральні значення на лініях і поверхнях. Розподіл температури може бути переданий в завдання розрахунку механічного напруженого стану (сполучена задача) або в завдання розрахунку нестаціонарного теплового поля.

Розв’язання задачі починається з побудови геометричної моделі процесу(рис.6а).

а)	б)

Рисунок 6 – Геометрична модель: а – побудова моделі; б – розбиття моделі на елементи.

Геометрична модель враховує лише розміри всіх частин об’єкту, який моделюється і може бути використана для вирішення будь-яких задач.

Другий етап – почергове виділення ділянок і визначення їх властивостей. Всі дані можуть бути або константами, або змінюватися в часі чи залежати від температури. Це теплоємність, теплопровідність,температуропровідність, щільність вугілля.

Третій етап – визначення граничних умов. Далі відбувається розбиття моделі на елементи. Модель готова.

а)

б)

Рисунок 7 – Результат розрахунків: а – з використанням ізотерм; б – з використанням кольорового зображення.

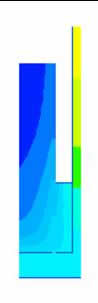
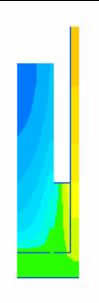
ELCUT проводить розрахунок і надає результат у вигляді кольорової картинки або рисунка з вказуванням ізотерм. Можна простежити зміну температури у часі (рис.7). ELCUT будує графіки (рис.8) і показує розрахункові таблиці, які можна передати до інших математичних чи статистичних програм. Наприклад, до MathCAD (рис.9).

0 сек	1000сек	2000сек
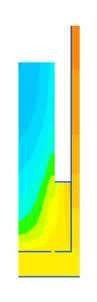
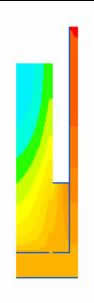
3000сек	4000сек	5000сек

Рисунок 8 – Розподіл температур по вугільному завантаженню у часі

Рисунок 9 – Розподіл температур у часі в одній точці вугільного завантаження

Рисунок 10 – Розподіл температури у вугільному завантаженні

 

Рисунок 11 – Сімейство температурних кривих по вугільному завантаженню.

Висновки:

В цій курсовій роботі було розглянуто процес коксування вугільного завантаження: фізико – хімічні перетворення вугілля в процесі термічної переробки; конструкції коксових печей, в яких відбувається цей процес.

Також було змодельовано процес коксування шихти та знайдено розподіл температур в процесі нагрівання вугілля і перехід його до якісно нового стану – коксу. Для цього були підібрані рівняння залежності теплофізичних параметрів різних марок вугілля та динасової вогнетривкої цегли (коефіцієнт теплопровідності, теплоємкість та щільність) від температури на основі яких проводився розрахунок коефіцієнта температуропровідності. На основі цих даних та диференціального рівняння було знайдено розподіл температур, в процесі коксування.

Нажаль, ця модель не враховує багатьох параметрів: температура простінка не постійна по довжині печі – всередині більша за температури с коксового та машинного боків; в процесі коксування відбувається кантовка і температура простінка змінюється в часі. Таким чином, ця модель дає приблизний час коксування, який дає лише можливість оцінити виробничість печі для даного складу шихти.

Для заданого складу вугілля (Г – 37%, Ж – 26%, К – 21%, ПС – 6%, Т – 10%) та розмірів камери коксування і стінки камери приблизний час складає 17.1 години. Слід зауважити, що реальний час коксування буде більшим.

 

ПЕРЕЛІК ПОСИЛАНЬ

Примітки: нижче наведений повний перелік посилань, з моєї магістерської роботи. Хоча не всі з них використані в тексті, я вирішив залишити їх з інформаційною метою - для зацікавлених осіб, щоб полегшити їм роботу з пошуку матеріалу.

1. Замолуев В.К., Касаточкин В.И. Изменение коэффициента температуропроводности каменных углей при изотермическом разложении // Кокс и химия, 1957. – № 6. – С. 21-23
2. Саранчук В.І., Ошовський В.В., Власов Г.О. Хімія і фізіка горючих копалин. – Донецьк.: Східний видавничий дім, 2003. – 204 с.
3. Скляр М.Г. Физико-химические основы спекания углей. – М.: Металлургия, 1983 – 200с
4. Агроскин А.А., Гончаров Е.И.. Определение теплоемкости углей в процессе коксования // Кокс и химия, 1965. – № 11. – С. 14–19
5. Агроскин А.А., Гончаров Е.И., Макеев Л.А., Якунин В.П. Теплоемкость и теплота реакций пиролиза углей Донбасса //  Кокс и химия, 1970. – № 5. – С. 8–13
6. Агроскин А.А., Глейбман В.Б. Теплофизика твердого топлива. – М.: Недра, 1980. – 256 с.
7. Агроскин А.А. Физика угля. – М.: Недра, 1965. – 238 с.
8. Батунер Л.М., Позин М.Е. Математические методы в химической технике. – Л.: Химия, 1968. – 824 с.
9. Тайц Е.М., Ермолаева Н.К., Николаев Ю.С. О спекаемости  углей и электросопротивлении кокса  // Кокс и химия, 1970. – №2. – С. 18-21
10. Гальперин В.В. Прибор для измерения удельного электросопротивления коксовых формовок // Кокс и химия, 1976. – №7. – С. 23-25
11. Слободской С.А. Роль показателя электросопротивления при оценке свойств углеродных материалов // Кокс и химия, 1999. – №2. – С.15-18
12. Касаточкин В.И., Ларина Н.К. Строение и свойства природных углей. – М.: Недра, 1976. – 318 с.
13. Скляр М.Г., Тютюнникова Ю.Б. Химия твердых горючих ископаемых. – К.: Вища школа, 1985. – 366 с.
14. Зубкова В.В., Еджиевич П., Гебска У. Влияние температуры нагревания ни изменение удельного электросопротивления твердых остатков термической деструкции спекающихся углей // Кокс и химия, 2000. – №9. – С. 16-22
15. Сапожников Л.М., Кармазин В.И. Изменение электропроводности угля в процессе коксования // ХТТ, 1931. – Вып. 8. – С. 69-77
16. Слободской С.А. Диэлектрометрическая оценка процесса термохимических превращений органических веществ каменных углей // Кокс и химия, 1998. – №4. – С. 7–9.
17. Брук А.С., Афанасьев М.В. О значении показателя электропроводности при определении качества кокса // Кокс и химия, 1936. –  №8. –  С. 31-36
18. Тайц Е.М., Ермолаева Н.К.,Николаев Ю.С. О спекаемости углей и электросопротивлении кокса // Кокс и химия, 1970. –  №3. –  С. 92-99
19. Агроскин А.А., Гончаров Е.И. Теплоемкость углей // Кокс и химия, 1965. –  № 7. –  С. 8-13 
20. Басов К.А. ANSYS: справочник пользователя. – М.: ДМК Пресс, 2005. – 640 с.
21. Лавриненко Н.М., Сукманов В.А., Афенченко Д.С., Шульга А.В. Конечно-элементное моделирование в расчетах деталей машин. Теория и практика. – Донецк.: ДонГУЭТ, 2006. – 475с.
22. Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курку процессы и аппараты химической технологии. – Л.: Химия, 1987. – 576 с.