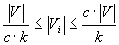|
abstract
The traditional problem about splitting graphs is focused on calculation of a k-phase segment
the column such, that division of edges is minimized, and each segment contains identical
quantity of tops (or, in case of weighed the column, each segment has the identical sum of
weights of tops). The problem of minimization of division of edges can be considered as the
purpose, and the requirement of that segments were the identical size, can be considered as
restriction. This one-target problem of splitting the column with one restriction is widely
used for static distribution of a network in scientific parallel modelling.
However, the column with one restriction is not enough this one-target problem of splitting
for computing requirements of many scientific imitating models. For example, in multiphase
net calculations not enough one restriction for effective balancing complex calculations.
Multiphase calculations consist from m separate computing phases, each of which is separated
by the certain step of synchronization. Basically, quantity of computing loading for each
element of a grid variously on different phases. Thus, for effective parallel performance
of these multiphase calculations, it is necessary so to divide a grid that calculations on
each phase have been balanced, and the quantity of interactions between various processors
on each phase has been minimized.
The key characteristic of this problem consists that it demands algorithm of the splitting
considering any quantity of restrictions, together with any quantity of the purposes
(minimization or maximization). [1]
For representation of many restrictions of balancing, it is necessary to expand traditional
model the column. Each top, instead of one weight, ассоциированного with it, has a vector of
weights. The size of this vector - m. This size corresponds to quantity of restrictions of
balancing. Using this added model the column, it is possible to formulate a problem of
splitting the column with many restrictions. To calculate k-phase splitting so that each
of m weights has been individually balanced with the established admission. [1]
Differently, if c - vector of the size m which defines the admission of disbalance of
loading then the purpose in this definition of a problem with many restrictions consists
in calculation of such segments such, that disbalance of loading concerning i-th weight
should be less than ci. For example, if we have two weights (m=2) then the vector of the
admission c = {1.05, 1.5} shows, that we search for splitting such in which disbalance of
loading concerning the first weight should be less or is equal 5 %, and for the second
weight - less or is equal 50%. [1]
Package METIS. METIS is the software package intended for splitting
greater irregular графов and calculation of orderings of rarefied matrixes. Algorithms in METIS
are based on multilevel splitting graphs. Algorithms of multilevel splitting reduce the size the
column by tightening tops and edges, break smaller columns, and then specify it for construction
of segments initial the column. METIS the column, and for improvement of splitting during a phase
of specification uses new decisions, both for consecutive reduction. During огрубления METIS uses
algorithms which simplify search of high-quality splitting in огрубленном (coarser graph). During
a phase of detailed elaboration METIS basically the column which is located most close to borders
is focused on that part. These strongly optimized algorithms allow METIS'у to find quickly
high-quality splittings for wide set graphs. [2]
Package METIS consists of several programs. For splitting графов in METIS is available two
programs: pmetis and kmetis. They are intended for splitting not structured графов on k-equal
parts. For splitting графов the program pmetis uses algorithm multilevel recursive бисекции
(see [3]). The program kmetis uses algorithm of multilevel k-phase splitting (see [4]). Both
these programs are capable to make high-quality splitting. However, depending on the entrance
data, one program can be more effective another. So, basically kmetis the column on more than
8 parts is more effective for splitting. For these problems kmetis essentially is faster, than
pmetis. In turn, pmetis the column on small quantity of parts is more effective for splitting.
[2]
The basic structure of multilevel k-phase splitting very simple. Columns G = (V, E) all over
again it is pulled together to small quantity of tops, then splitting it much more smaller the
column and after that the received splitting is projected back in original columns, by consecutive
improvements at each level pays off. Work of algorithm is presented in figure 2.1.
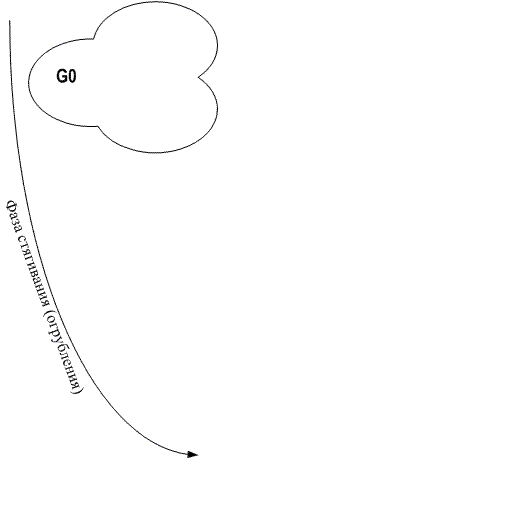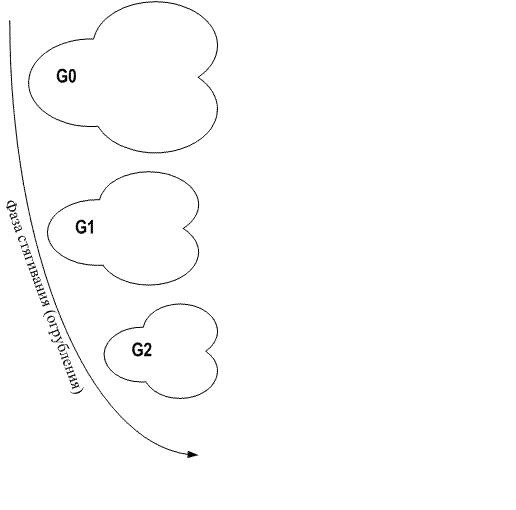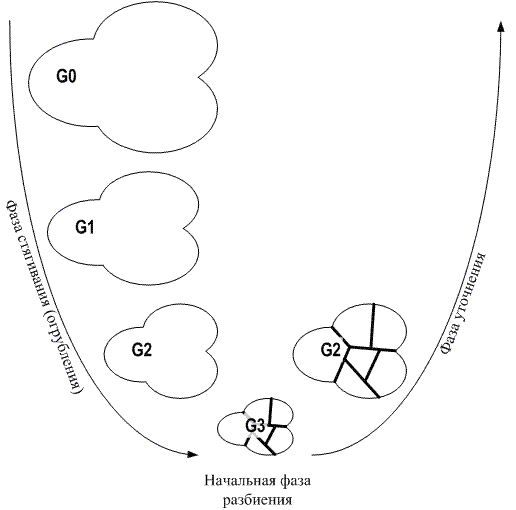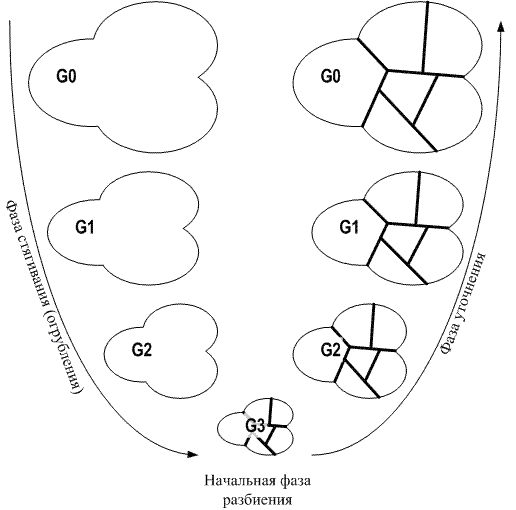
figure 2.1 - Multilevel k-phase splitting.
Phase of tightening. On a phase of tightening , from original column
G0 = (V0, E0) is under construction sequence smaller графов
Gi = (Vi, Ei) such, that |Vi+1| < |Vi|.
In the majority of schemes of tightening, set of tops column Gi are united in one
top of following level Gi+1 strapped the column. Let Viv - set
of tops column Gi incorporated for formation of top v column Gi+1. That
splitting strapped the column was good concerning to original the column, weight of top v is
established equal to the sum of weights of tops from set Viv. Also, for
preservation of the information on communications in strapped to the column, edges of top v are
association of edges of tops from set Viv. In case of when more than one
top from set Viv has an edge connected with same top u, weight of an
edge {u, v} it is equal to the sum of weights of these edges. This method of tightening
(огрубления) possesses following properties [4, 5]:
- borders of splittings in strapped to the column are equivalent to borders of the same
splittings in specified to the column;
- equation of splittings strapped графов leads to equation of splittings specified графов.
Phase of initial splitting. The second phase of algorithm of multilevel
k-phase splitting is a calculation of k-phase splitting Pm strapped column Gm
= (Vm, Em) such, that each segment the column contains approximately
|V0| / k weights of tops original. During tightening weight of tops and edges огрубленного
the column have been chosen so that to reflect weights of tops and edges original the column. Thus,
Gm contains the adequate information for satisfaction of requirements of equation of
splitting and minimal requirements to borders of splittings. [4]
One of variants of reception of initial k-phase splitting is a continuation of tightening the
column until in it will not remain k tops. These strapped k tops can serve as initial k-phase
splitting original the column. There are two problems with such decision. First, for the
majority графов reduction of the size the column on each step огрубления becomes very small
after several steps that does expensive each subsequent step. Secondly, even if there is an
opportunity to pull together columns of all up to k tops, weights of these tops most likely
will be rather various, that will make initial splitting strongly debalanced. [4]
In package METIS, initial splitting is calculated by means of multilevel бисекционного algorithm.
Experiments of authors of a package have shown, that this algorithm gives quite good initial
splitting, with rather small expenses of time. [4]
Phase of specification. During a phase of specification splitting
Pm strapped column Gm is projected back in original columns, passing
through columns Gm-1, Gm-2, Gm-3, ... G1. As each
top v from Gi+1 contains the certain subset of tops Viv from
Gi Pi it is received from Pi+1 by simple giving of set of tops
Viv to segment Pi+1[v], i.e. Pi[u] := Pi+1[v],
for all u Є Viv. [4]
It is necessary to note, that even if splitting Gi is in the local minimum, projected
splitting Gi-1 can not be in a local minimum. As Gi-1 it is more detailed,
it has more degrees of freedom which can be used for additional improvement splitting and
consequently and for reduction of quantity of divided edges.
Class of algorithms of local specification which tend to reception of good results are the
algorithms based on algorithm Кернигана-Лина and its updatings [6, 7, 8]. Algorithm
Кернигана-Лина пошагово exchanges tops between segments бисекции for reduction of quantity
of divided edges between segments until splitting will not reach a local minimum.
In package METIS the algorithms of specification developed by authors of a package are used
simple k-phase. These algorithms are the simplified versions of k-phase algorithm of
specification Кернигана-Лина. Complexity of the developed algorithms does not depend on
quantity of segments which are necessary for specifying.
Package hMETIS. The package hMETIS is intended for splitting
гиперграфов (see [9]). hMETIS is a multilevel algorithm бисекции the hypercolumn. Formally,
hypercolumns G = (V, E) it is defined as set of tops V and set of hyperedges E where each
hyperedge is a subset of set of edges V, and the size of a hyperedge is a capacity of this
subset (see [10]).
Problem which solves algorithm hMETIS, it is possible to define as follows. Is available
hypercolumns G = (V, E), where V - set of tops and E - set of hyperedges. There is an admission
(in the document khmetis.pdf; the explanatory of this factor is the formula presented below)
of the general disbalance of loading c, such, that c >= 1.0. The purpose - to find splitting
set V on k not crossed subsets. V1, V2, ..., Vk - such, that
the quantity of tops in each set Vi is limited by an inequality:
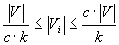
The criterion function certain for all the hypercolumn, should be optimized.
hMETIS, also as well as the algorithm of multilevel k-phase splitting in package METIS, has three
phases: tightening, initial splitting and specification. On a phase of tightening two schemes
are used:
- tightening edges (edge-coarsening);
- tightening hyperedges (hyperedge-coarsening).
The first scheme chooses groups by search of pairs tops which belong to many hyperedges. In this
scheme each group consists, at least, of two tops, and each top belongs, at least, to one group.
The second scheme finds as much as possible independent set of hyperedges, and sets of tops which
belong to each hyperedge, become group of tops which should be strapped. The example of performance
of tightening the hypercolumn is shown in figure 2.2.
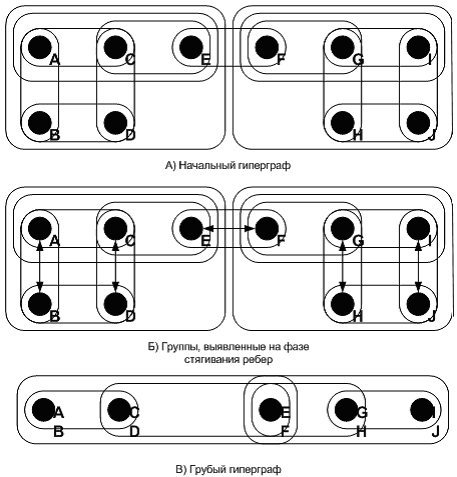
Figure 2.2
- the Example of performance of tightening the hypercolumn.
The phase of search of initial splitting in hMETIS is equivalent to a phase of splitting
in multilevel k-travelling algorithm of splitting графов. On a phase of specification segments strapped
the hypercolumn are projected on a following level specified the hypercolumn, and for optimization of
criterion function without infringement of restriction of balancing of splitting the algorithm of
specification is used.
In case of бисекционного specifications, algorithm FM shows good enough results (see [11]).
For each top v algorithm FM calculates "benefit" (gain) which is decrease in value of criterion
function, достигаемым moving of top v in other segment. These tops are located in two turns with
priorities, each of which corresponds to one segment according to the calculated benefit. In the
beginning all tops are unblocked, i.e. they can be moved from one segment to another. The algorithm
пошагово chooses the unblocked top with greatest "benefit" from one of two priority turns, and moves
it to other segment. After moving the top v becomes blocked, and "benefits" of tops, adjacent with v,
are updated. After each moving top the algorithm writes down value of the criterion function, received
on a current step. One pass of algorithm comes to an end, when there are no unblocked tops more. After
that the written down values of criterion function are checked, and that step when criterion function
had the minimal value gets out. All the tops moved to other segments after that a step come back back
in the initial segments. After that, the received splitting becomes initial for following pass of
algorithm.
However specification of k-phase splitting is much more complex, because tops can move from
one segment to set of others, that комбинаторно increases space of optimization. Expansion for
algorithm FM for a case of k-phase specification is described in [12]. This algorithm uses k(k-1)
priority turns on one for each type of moving. On each step of algorithm in each of k(k-1) there
are movings with greatest "benefit". Moving with greatest "benefit" which keeps is carried out
or improves a condition of balance. After performance of moving each of k(k-1) turns is updated.
Complexity of k-travelling specification considerably above, than for two travelling specifications.
Authors of a package hMETIS have developed the algorithm of specification - "greedy" algorithm
of splitting. It carries out set of iterations. On each iteration tops for definition are checked
all, whether they can be moved so that criterion function was optimized at preservation of a condition
of balance.
The algorithm works as follows. We shall present hypercolumns Gi = (Vi, Ei)
and its vector of splitting Pi. Tops are looked through in the casual order. Let v such top,
where Pi[v] = a - a segment to which posesses top v. If v is internal unit of a segment a the
top does not move. If v is on border of a segment then v can be potentially moved to one of segments
N(v) in which there are tops, adjacent with v. Let N'(v) - subset N(v) which contains all segments b,
such, that moving of top v in a segment b does not break a condition of balance. Then the segment
b Є N'(v) which leads to the greatest positive reduction (benefit) in criterion function gets out,
and the top v moves to it.
Package ParMETIS. PARMETIS is the parallel library based on MPI - Message
Passing Interface - the report of an exchange of messages between the processes which are carried out
in parallel which realizes a set of algorithms for splitting and переразбиения not structured графов
and calculations of orderings of the rarefied matrixes. PARMETIS it is partially suitable for the
parallel numerical models containing greater not structured grids.
Algorithms in PARMETIS are based on multilevel splitting which have been realized in package METIS.
However PARMETIS expands the functionality given by package METIS and includes subroutines which are
mainly intended for parallel calculations of is wide-scale numerical models. [13]
Parallel algorithm of splitting графов. The parallel algorithm also
consists of three phases, as well as the algorithms described above. But at each level of tightening
the column is calculated раскраска. This раскраска is used for elimination of conflicts in calculation
of a global combination on a phase of tightening, and also for elimination of superfluous movings tops
at the k-phase specification which is carried out on a phase of specification. As tops of one color
form independent set this scheme guarantees, that each moving of top will lead to reduction of quantity
of the cut edges. Besides in algorithm the column for even greater decrease already and so small time
of performance of this phase is used распараллеливание algorithm of initial splitting.
Let p - quantity of processors for calculation of O-phase splitting column G = (V; E). G it is
originally distributed between processors, using the unidirectional distribution so, that each
processor receives n=p tops and lists of their contiguity. In the end of algorithm number of
a segment is appropriated to each top the column.
Раскраска the column. Раскраска column G = (V; E) column G so appropriates
colors to tops, that adjacent tops have various colors. In ParMETIS it is searched such раскраска that
the quantity of separate used colors was small. The parallel algorithm раскраски, developed by authors
ParMETIS, includes some iterations. In each iteration as much as possible independent set of tops I gets
out with use of changed algorithm Луби (see [15]). To all tops in independent set identical color is
appropriated. Before the beginning of following operation of top from set I leave from the column, and
formed smaller columns becomes entrance графом for following iteration. As much as possible independent
set I of set of tops S is calculated in the incremental order, using algorithm Луби as follows.
To each top the random number and if the top receives casual number which is less, than all numbers
of adjacent tops this top joins in set I is appropriated. After that process repeats for tops from
set S which do not enter into set I, and are not adjacent with tops from I, and I extends in a similar
way. This incremental escalating of set I comes to an end when there are no tops which can be inserted
in I more. In [15] it is shown, that one iteration of algorithm Луби demands all O (log |S|) such
expanding steps for search of as much as possible independent set of tops from set S.
In ParMETIS algorithm Луби is realized for parallel раскраски. In it the phase of installation of
connection in which structures of data for the help of process of an exchange are created by casual
numbers is carried out. In particular, in algorithm it is predetermined, what tops are on border
between processors and what are internal tops. These structures of data are used in all phases of
parallel algorithm of splitting графов.
Phase огрубления (tightening). The parallel algorithm of tightening
is based on expansion of consecutive algorithm and the column for structurization of sequence
of calculations uses раскраску. It is given columns Gi = (Vi ; Ei)
which has been painted with use of parallel algorithm Луби. Let Match is the variable connected
with each top the column which in the beginning matters -1. In the end of calculations, variable
Match (Matсh it is a file) for each top v contains number of top from which the top v should be
strapped. If v it is not pulled together, Match = v.
Value Mi (it is variable Matchi or Match[i]) is calculated is iterative.
In current of c-th iteration, top of color c, which for the present have not been connected
(i.e., Match = -1), choose one of the untied neighbours, using heavy-edge heuristics
(i.e. heuristics " edges of the heavyweight "), and modify variable Match of the chosen top
installation in numbers. Let v - top of color c, and (v; u) - an edge chosen by top v. As color
of top u not c (I paint - if the top v has color c and it is connected by an edge with top u should
not have color c, according to statement of a problem of colouring the column), this top (u - top;
c - some color) will not choose to itself the partner on the given iteration. However, there is an
opportunity, that other top w colors c can choose an edge (w; u). As both tops v and w carry out
the choice simultaneously (on the same iterations) such situation will not occur because the
choice occurs on the same iterations; consistently top v will establish Match[u] := v, and then
the top w will establish Match[u] := w; last established value will be used - to look following
offers. It is fulfilled as follows. After all tops of color c will choose untied neighbours, they
are synchronized. Tops of color c which have just chosen the neighbour, read value variable Match
the chosen top. If the read through value is equal to their number of top connection is executed
successfully, and they establish variables Match equal to the chosen top; otherwise connection
is considered unfortunate, and the top becomes not adhered. It is necessary to note, that if
more than one top (for example, v and w) wishes to adhere to itself one and туже top (for example,
u) only one of them will successfully finish connection; and it defines, what connections will
remain. However, use раскраски limits a choice to tops of the partners on each iteration. So,
the quantity of similar disputed situations considerably decreases. Also it is necessary to note,
that even if the top of color c can unsuccessfully end connection because of conflicts, this top
can be all the same attached in current of the subsequent iterations.
Phase of splitting. During a phase of splitting, p-phase splitting
is calculated with use recursive бисекционного algorithm. As огрубленный columns has only O(p)
tops, this step can be executed consistently (i.e., not in parallel), without significant
influence on productivity of all algorithm. Nevertheless, in ParMETIS this phase also
распараллеливается with use of recursive decomposition. It is carried out as follows: various
parts rough the column gather on all processors with use of broadcasting operation. During this
moment processors carry out recursive бисекцию, using the algorithm based on the enclosed section
(see [16]) and greedy specification of splitting. However each processor develops only one way of
a tree recursive бисекции. In the end each processor accumulates tops which correspond to their
segments of p-phase splitting. It is necessary to note, that after broadcasting operation, the
algorithm works without what or additional communications between processors.
Phase of specification. On a phase of specification, splitting is
projected with rough the column on a following level detailed the column and specified with
use of greedy algorithm of specification. During one phase of specification in consecutive
algorithm pass on casual tops is carried out, and they move to segments that conducts to
greater reduction of a cut of edges. In parallel execution of greedy specification the
procedure for test of tops for an opportunity of their moving to other segments is changed.
In particular, one phase of algorithm of specification is broken on c under-phases where
c is a quantity of colors specified the column. During i-th phase all tops of color i are
considered on opportunity of moving, and a subset of those tops which conduct to reduction
of quantity of the cut tops, move. Since tops with identical color form independent set the
general reduction of quantity of the cut edges, received by moving of tops to the same moment
of time, is equivalent to the sum уменьшений quantities of the cut edges received by moving
of these tops consistently one for another. After performance of this group of movings external
degrees of tops, adjacent with the given group are updated, and behind that following color
is processed.
In work methods of splitting графов the big dimension with many restrictions which are used
in packages METIS, ParMETIS and hMETIS are considered. It is established, that all these
packages use updatings the same algorithms. This multilevel algorithm consists of three phases:
- tightening the column - for reception rough reduced the column;
- initial splitting - reception of splitting reduced the column;
- specification - reception of splitting initial the column by consecutive displaying splittings
into the detailed columns of each level, and by specification of splitting at each level.
Package METIS uses consecutive algorithm for splitting графов. The package hMETIS uses the same
algorithm, but modified for search of splittings on the hypercolumn. Package ParMETIS uses parallel
algorithm of splitting which is similar on consecutive, but uses algorithm раскраски графов, necessary
for the prevention of many disputed situations caused распараллеливанием.
the list of the literature
[1] George Karypis, Vipin Kumar. Multilevel Algorithms for Multi-Constraint Graph Partitioning.
University of Minnesota, Department of Computer Science / Army HPC Research Center. Minneapolis,
MN 55455. Technical Report # 98-019.
[2] George Karypis. Vipin Kumar. METIS. A Software Package for Partitioning Unstructured Graphs,
Partitioning Meshes, and Computing Fill-Reducing Orderings of Sparse Matrices Version 4.0. -
University of Minnesota: September 20, 1998.
[3] G. Karypis and V. Kumar. A fast and highly quality multilevel scheme for partitioning irregular
graphs. SIAM Journal on Scientific Computing, 1998 (to appear). Also available on WWW at URL
http://www.cs.umn.edu/?karypis. A short version
appears in Intl. Conf. on Parallel Processing 1995.
[4] G. Karypis and V. Kumar. Multilevel k-way partitioning scheme for irregular graphs. Journal
of Parallel and Distributed Computing, 48(1):96-129, 1998. Also available on WWW at URL
http://www.cs.umn.edu/?karypis.
[5] Bruce Hendrickson and Robert Leland. The chaco user's guide, version 1.0. Technical Report
SAND93-2339, Sandia National Laboratories, 1993.
[6] B. W. Kernighan and S. Lin. An efficient heuristic procedure for partitioning graphs. The
Bell System Technical Journal, 49(2):291-307, 1970.
[7] C. M. Fiduccia and R. M. Mattheyses. A linear time heuristic for improving network partitions.
In In Proc. 19th IEEE Design Automation Conference, pages 175-181, 1982.
[8] Bruce Hendrickson and Robert Leland. A multilevel algorithm for partitioning graphs. Technical
Report SAND93-1301, Sandia National Laboratories, 1993.
[9] George Karypis, Vipin Kumar. Multilevel k-way Hypergraph Partitioning. - Department of Computer
Science & Engineering; Army HPC Research Center; University of Minnesota, Minneapolis, MN 55455.
Technical Report #98-036.
[10] Charles J. Alpert and Andrew B. Kahng. Recent directions in netlist partitioning. Integration,
the VLSI Journal, 19(1-2):1-81, 1995.
[11] C. M. Fiduccia and R. M. Mattheyses. A linear time heuristic for improving network partitions.
In In Proc. 19th IEEE Design Automation Conference, pages 175-181, 1982.
[12] L. A. Sanchis. Multiple-way network partitioning. IEEE Transactions on Computers, pages 62-81, 1989.
[13] George Karypis, Kirk Schloegel and Vipin Kumar. PARMETIS Parallel Graph Partitioning and Sparse
Matrix Ordering Library, Version 3.0. - University of Minnesota, Department of Computer Science and
Engineering, Army HPC Research Center, Minneapolis, MN 55455: March 28, 2002.
[14] George Karypis, Vipin Kumar. Parallel Multilevel k-way Partitioning Scheme for Irregular Graphs.
- University of Minnesota, Department of Computer Science / Army HPC Research Center, Minneapolis,
MN 55455, Technical Report: 96-036.
[15] Michael Luby. A simple parallel algorithm for the maximal independent set problem. SIAM Journal
on Computing, 15(4):1036-1053, 1986.
[16] A. George. Nested dissection of a regular finite-element mesh. SIAM Journal on Numerical Ananlysis,
10:345-363, 1973.
|