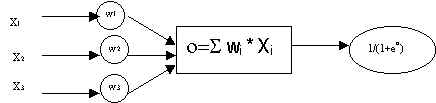Корнеев Д С Использование аппарата нейронных сетей для создания модели оценки иуправления рисками предприятия

Классификация рисков и обзор существующих методов анализа

Риск – возможное нежелательное событие (или класс возможных нежелательных событий), под действием которого объект управления может перейти в нежелательное состояние (называемое рисковой ситуацией). При этом под реализацией риска понимается появление события риска и переход объекта управления в нежелательное состояние под влиянием этого события.

В зависимости от возможного результата (рискового события) риски можно поделить на две большие группы: чистые и спекулятивные.

Чистые риски означают возможность получения отрицательного или нулевого результата. К этим рискам относятся следующие риски: природно-естественные, экологические, политические, транспортные и часть коммерческих рисков (имущественные, производственные, торговые).

Спекулятивные риски выражаются в возможности получения как положительного, так и отрицательного результанта. К этим рискам относятся финансовые риски, являющиеся частью коммерческих рисков.

В зависимости от основной причины возникновения рисков (базисный или природный риск) они делятся на следующие категории: природно-естественные риски, экологические, политические, транспортные, коммерческие риски.

Теория управления рисками (страхование и риск-менеджмент) занимается выявлением источников потерь, исследованием логики и вероятности возникновения событий риска, а также разрабатывает механизмы компенсации сопутствующих им потерь.

Основным механизмом управления рисками и потерями от них является хеджирование. Под хеджированием понимается динамическая стратегия управления объектом, подверженным влиянию рисков (стратегия хеджа), обеспечивающая с заданной степенью точности количественную оценку возможности попадания объекта управления в рисковую ситуацию и ограничивающая в случае реализации риска размеры потенциальных потерь до заданного уровня (вплоть до полного устранения потерь с вероятностью 1 – это т.н. совершенный хедж)[1]. Анализ развития математических методов и средств измерения и управления финансовыми рисками, применяемых ведущими мировыми корпорациями, показывает, что с начала 90-х гг. наблюдается массовое внедрение в практику статистических моделей оценки потерь от рыночного риска VaR (Value-At-Risk) [2].

Границы применимости статистических моделей риска были осознаны во кризиса 1998-99 гг., сопровождавшегося крахом некоторых крупных финансовых организаций, полагавшихся на статистические модели риска. [3]

В свете этого высказывания и опыта недавних финансовых кризисов одним из перспективных подходов к управлению рисками является применение аппарата нейронных сетей для классификации и прогнозирования рисков. В следующем разделе будут более подробно разобраны недостатки существующих эконометрических моделей и описаны преимущества нейросетевой технологии.

Нейронные сети и их преимущества для решения задачи оценки рисков

На практике при анализе рисков часто встречаются задачи, связанные с наблюдением случайных величин. Для подобных задач не удается построить детерминированные модели, поэтому применяется принципиально иной, вероятностный подход. Параметры вероятностных моделей - это распределения случайных величин, их средние значения, дисперсии и т.д. Как правило, эти параметры изначально неизвестны, а для их оценки используются статистические методы, применяемые к выборкам наблюдаемых значений (историческим данным).

К сожалению, классические методики оказываются малоэффективными во многих практических задачах. Это связано с тем, что невозможно достаточно полно описать реальность с помощью небольшого числа параметров модели, либо расчет модели требует слишком много времени и вычислительных ресурсов. В частности, рассмотрим проблемы, возникающие при решении задачи оптимального распределения инвестиций.

В реальной задаче ни одна из функций не известна точно - известны лишь приблизительные или ожидаемые значения прибыли. Для того, чтобы избавиться от неопределенности, мы вынуждены зафиксировать функции, теряя при этом в точности описания задачи.

Детерминированный алгоритм для поиска оптимального решения (симплекс-метод) применим только в том случае, если все данные функции линейны. В реальных задачах оценки рисков это условие не выполняется. Хотя данные функции можно аппроксимировать линейными, решение в этом случае будет далеким от оптимального.

Если одна из функций нелинейна, то симплекс-метод неприменим, и остается два традиционных пути решения этой задачи.

Первый путь - использовать метод градиентного спуска для поиска максимума прибыли. В данном случае область определения функции прибыли имеет сложную форму, а сама функция - несколько локальных максимумов, поэтому градиентный метод может привести к неоптимальному решению. Второй путь - провести полный перебор вариантов инвестирования. Если каждая из 10 функций задана в 100 точках, то придется проверить около 10²⁰ вариантов, что потребует не менее нескольких месяцев работы современного компьютера.

Отметим также, что статистические методы хорошо развиты только для одномерных случайных величин. Если же мы хотим учитывать несколько взаимосвязанных факторов, то придется обратиться к построению многомерной статистической модели. Однако такие модели либо предполагают гауссовское распределение наблюдений (что не выполняется на практике), либо не обоснованы теоретически.

Таким образом приходим к необходимости применения усовершенствованного математического аппарата.

Применение нейросетевой технологии уместно в случаях, когда формализация процесса решения трудна или вообще невозможна. Они являются очень мощным инструментом моделирования поскольку нелинейны по своей природе. Как уже было сказано, линейные моделирование долгое время являлось основным в большинстве областей, поскольку для него существует большое число методов оптимизации. Однако для задачи анализа рисков предположение о линейной сепарабельности исходных данных в подавляющем большинстве случаев оказывается неверным. Кроме того для нейронных сетей не существует проблемы «проклятия размерности», не позволяющее моделировать линейные зависимости от большого числа переменных.

Нейронная сеть применяется в первую очередь тогда, когда неизвестен точный вид связи между входом и выходом. Достаточно лишь точно знать, что связь между входными и выходными данными существует. При этом сама зависимость будет выведена в процессе обучения нейронной сети.

Подводя итог вышесказанному, по сравнению с традиционными технологиями нейронные сети обладают следующими преимуществами:

· Универсальность. Нейронные сети не зависят от свойств входных данных, для них не существует требования к определенному типу распределения исходных данных, либо требования к линейности целевых функций.

· Не существует проблемы «проклятия размерности». Они способны моделировать зависимости в случае большого числа переменных.

· В отличие от статистических исследований не требуют большого объема данных.

· Ускоряют процесс нахождения зависимости за счет одновременной обработки данных всеми нейронами. Особенности построения нейронных сетей будут рассмотрены далее.

Несмотря на то, что нейронные сети способны решить практически любые задачи, во многих случаях их применение не является целесообразным. Для большинства задач более эффективным оказывается применение других математических моделей. Нейронные сети особенно хорошо зарекомендовали себя при решении задач классификации, прогнозирования, кодирования и декодирования информации.

Для управления рисками наиболее целесообразно применение нейронных сетей в следующих областях:

· Оценка производственных рисков. Прогнозирование необходимого запаса сырья. Оптимальное планирование производства.

· Оценка инвестиционных рисков. Анализ организационно-экономической устойчивости предприятий и прогнозирование банкротств.

· Оценка валютных рисков. Прогнозирование котировок на валютном рынке

· Оценка кредитных рисков. Прогноз эффективности кредиования.

· Оценка торговых рисков. Исследование фактора спроса. Прогнозирование и анализ цен. Прогнозирование продаж.

Начнем с рассмотрения биологического прототипа – нейрона[15]. Нейрон является нервной клеткой биологической системы. Он состоит из тела и отростков, соединяющих его с внешним миром.

Отростки, по которым нейрон получает возбуждение, называются дендритами. Отросток, по которому нейрон передает возбуждение, называется аксоном, причем аксон у каждого нейрона один. Дендриты и аксон имеют довольно сложную ветвистую структуру. Место соединения аксона нейрона - источника возбуждения с дендритом называется синапсом. Основная функция нейрона заключается в передаче возбуждения с дендритов на аксон. Но сигналы, поступающие с различных дендритов, могут оказывать различное влияние на сигнал в аксоне. Нейрон выдаст сигнал, если суммарное возбуждение превысит некоторое пороговое значение, которое в общем случае изменяется в некоторых пределах. В противном случае на аксон сигнал выдан не будет: нейрон не ответит на возбуждение. У этой основной схемы много усложнений и исключений, тем не менее, большинство искусственных нейронных сетей моделируют лишь эти простые свойства.

Искусственный нейрон

Искусственный нейрон имитирует в первом приближении свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, аналогичный синаптической силе, и все произведения суммируются, определяя уровень активации нейрона. На рис. 1.2 представлена модель, реализующая эту идею. Хотя сетевые парадигмы весьма разнообразны, в основе почти всех их лежит эта конфигурация. Здесь множество входных сигналов, обозначенных x1, x2,:, xn, поступает на искусственный нейрон. Эти входные сигналы, в совокупности, обозначаемые вектором X, соответствуют сигналам, приходящим в синапсы биологического нейрона. Каждый сигнал умножается на соответствующий вес w1, w2,..., wn, и поступает на суммирующий блок. Каждый вес соответствует "силе" одной биологической синаптической связи. (Множество весов в совокупности обозначается вектором W.) Суммирующий блок, соответствующий телу биологического элемента, складывает взвешенные входы алгебраически, создавая выход, который мы будем называть NET. В векторных обозначениях это может быть компактно записано следующим образом:

NET = XW.

Активационные функции

Сигнал NET далее, как правило, преобразуется активационной функцией F и дает выходной нейронный сигнал OUT. Активационная функция может быть обычной линейной функцией

OUT = K(NET),

где К - постоянная, пороговой функции

OUT = 1, если NET > T,
OUT = 0 в остальных случаях,

где Т - некоторая постоянная пороговая величина, или же является функцией, более точно моделирующей нелинейную передаточную характеристику биологического нейрона и представляющей нейронной сети большие возможности.

Если функция F сужает диапазон изменения величины NET так, что при любых значениях NET значения OUT принадлежат некоторому конечному интервалу, то F называется "сжимающей" функцией. В качестве "сжимающей" функции часто используется логистическая или "сигмоидальная" (S-образная) функция. Эта функция математически выражается как F(x) = 1/(1 + е-x). Таким образом,

OUT=1/(1+e-NET)

Искусственная нейронная сеть (ИНС, нейронная сеть) - это набор нейронов, соединенных между собой. Как правило, передаточные функции всех нейронов в нейронной сети фиксированы, а веса являются параметрами нейронной сети и могут изменяться. Некоторые входы нейронов помечены как внешние входы нейронной сети, а некоторые выходы - как внешние выходы нейронной сети. Подавая любые числа на входы нейронной сети, мы получаем какой-то набор чисел на выходах нейронной сети. Таким образом, работа нейронной сети состоит в преобразовании входного вектора в выходной вектор, причем это преобразование задается весами нейронной сети [4].

При выборе числа входов нейронной сети следует учитывать это, выбирая разумный компромисс между глубиной предсказания (число входов нейронной сети) и качеством обучения нейронной сети (объем тренировочного набора).

Нелинейная активационная функция

Многослойные сети не могут привести к увеличению вычислительной мощности по сравнению с однослойной сетью лишь в том случае, если активационная функция между слоями не будет линейной. Вычисление выхода слоя заключается в умножении входного вектора на первую весовую матрицу с последующим умножением (если отсутствует нелинейная активационная функция) результирующего вектора на вторую весовую матрицу.

(XW1)W2

Так как умножение матриц ассоциативно, то

X(W1W2).

Это показывает, что двухслойная линейная сеть эквивалентна одному слою с весовой матрицей, равной произведению двух весовых матриц. Следовательно, любая многослойная линейная сеть может быть заменена эквивалентной однослойной сетью. Однослойные сети весьма ограниченны по своим вычислительным возможностям. Таким образом, для расширения возможностей сетей по сравнению с однослойной сетью необходима нелинейная активационная функция.

Обучение искусственных нейронных сетей

Среди всех интересных свойств искусственных нейронных сетей ни одно не захватывает так воображения, как их способность к обучению. Их обучение до такой степени напоминает процесс интеллектуального развития человеческой личности, что может показаться, что достигнуто глубокое понимание этого процесса. Но, проявляя осторожность, следует сдерживать эйфорию. Возможности обучения искусственных нейронных сетей ограниченны, и нужно решить много сложных задач, чтобы определить, на правильном ли пути мы находимся.

Пример разработки модели нейронной сети для анализа риска наступления банкротства предприятия.

Краткое описание традиционных методов предсказания банкротства.

Первые попытки разработать модель предсказания банкротства, используя методы одномерной статистики, были предприняты Бивером в 1966 году[18]. Ключевыми этапами в разработке таких моделей стали многомерный анализ Альтмана(1968)[12], многомерный дискриминантный анализ Эдмистера, логит-преобразование Ольсона, рекурсивный разделяющий алгоритм, описанные в [13].

Преимущество рекусивного алгоритма перед многомерным дискриминантным анализом и логии-преобразованием заключается в том, что взаимовлияние переменных включено в модель. Комбинации переменных и пороговых значений оцениваются на большом числе возможных точек ветвления. Все возможные комбинации оцениваются рекурсивным алгоритмом и выбираются те, которые наиболее эффективны для прогнозирования. Результатом является модель в виде дерева.

При применении традиционных методов математики испытывают трудности в определении и оценке подходящей модели. Задача прогнозирования банкротства нередко вызывает споры у исследователей относительно подходящей функциональной формы уравнений. Зачастую они солидарны лишь в том, что это модель является сложной. Скорее всего, выяснение наилучшей модели для прогнозирования является не решаемой задачей. Существует ряд факторов осложняющих определение и оценку лучшей модели:

· Сложность существующих моделей ограничена используемыми способами оценки. Поэтому эти способы выступают как ограничения, которые являются препятствием для аналитиков при выборе оптимальной модели. Выбор с пользу той или иной модели порой осуществляется исходя из вычислительной сложности алгоритма, а не точности модели. Так, например, линейность зачастую «навязывается» исходным данным, не потому что было проведено детальное исследование, с целью выяснить зависимости между переменными, а просто из-за простоты существующей для таких исходных данных процедуры оценки.

· Стандартные методы оценки работают при условии нормального распределения совокупности исходных данных. Многочисленные исследования показывают, что финансовые коэффициенты, используемых в прогнозировании несостоятельности, не распределены по гауссовому закону.

· Преобразования, применяемые к исходным данным отчетности, иногда не в состоянии отразить неочевидные взаимосвязи между переменными.

В рамках данной работы автором разработана конфигурация на базе известной модели нейронной сети для оценки инвестиционных рисков.

Модель нейронной сети для предсказания финансовой несостоятельности организации.

Для построения нейронной сети необходимо разработать ее топологию, определить механизм обучения и процедуру тестирования. Кроме того для обучения нужны входные данные – выборка компаний с достоверной финансовой отчетностью и рассчитанные на ее основе коэффициенты.

Наиболее привлекательным в данном случае представляется выбор трехслойного персептрона и алгоритма обратного распространения в качестве обучающего.

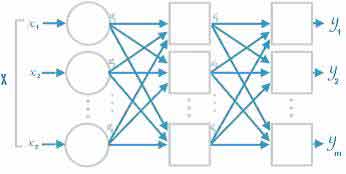
Этот тип нейронных сетей довольно хорошо исследован и описан в научной литературе. Он была предложена в работе Rumelhart, McClelland (1986) и подробно обсуждается почти во всех учебниках по нейронным сетям (см., например [16]). Каждый элемент сети строит взвешенную сумму своих входов с поправкой в виде слагаемого и затем пропускает эту величину активации через передаточную функцию, и таким образом получается выходное значение этого элемента. Элементы организованы в послойную топологию с прямой передачей сигнала. Такую сеть легко можно интерпретировать как модель вход-выход, в которой веса и пороговые значения (смещения) являются свободными параметрами модели. Такая сеть может моделировать функцию практически любой степени сложности, причем число слоев и число элементов в каждом слое определяют сложность функции. Определение числа промежуточных слоев и числа элементов в них является важным вопросом при конструировании MLP [16]. Количество входных и выходных элементов определяется условиями задачи.

Самый известный вариант алгоритма обучения нейронной сети - так называемый алгоритм обратного распространения (back propagation; [20]). В алгоритме обратного распространения вычисляется вектор градиента поверхности ошибок. Этот вектор указывает направление кратчайшего спуска по поверхности из данной точки, поэтому если мы "немного" продвинемся по нему, ошибка уменьшится. Последовательность таких шагов (замедляющаяся по мере приближения к дну) в конце концов приведет к минимуму того или иного типа. Определенную трудность здесь представляет вопрос о том, какую нужно брать длину шагов.

При большой длине шага сходимость будет более быстрой, но имеется опасность перепрыгнуть через решение или уйти в неправильном направлении. Классическим примером такого явления при обучении нейронной сети является ситуация, когда алгоритм очень медленно продвигается по узкому оврагу с крутыми склонами, прыгая с одной его стороны на другую. Напротив, при маленьком шаге, вероятно, будет схвачено верное направление, однако при этом потребуется очень много итераций. На практике величина шага берется пропорциональной крутизне склона (так что алгоритм замедляет ход вблизи минимума) с некоторой константой, которая называется скоростью обучения. Правильный выбор скорости обучения зависит от конкретной задачи и обычно осуществляется опытным путем; эта константа может также зависеть от времени, уменьшаясь по мере продвижения алгоритма.

Конфигурация разработанной сети следующая:

Общие параметры	Параметры скрытого слоя	Параметры выходного слоя
Количество узлов во входном слое:10	Коэффициент обучения: 0.25	Коэффициент обучения: 0.01
Число узлов в скрытом слое:10	Коэффициент инерции: 0.6	Коэффициент инерции: 0
Число узлов в выходном слое:1	Затухание:0	Затухание:0
Алгоритм обучения: Обратное распространение
Функция активации: сигмоидальная

Точность подбора этих параметров определяет способность сети к обучению. Входные узлы соответствуют финансовым коэффициентам, используемым для предсказания несостоятельности. Значение единственного узла выходного слоя – показатель финансовой состоятельности предприятия. Единичное значение соответствует состоянию банкротства, нулевое – полному финансовому благополучию. В качестве активационной функции выбрана сигмоидальная:

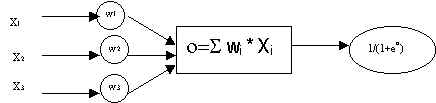
wpe4.jpg (6305 bytes)

В качестве входных данных используется разработанный автором набор финансовых коэффициентов. В качестве базовых использовались параметры модели Альтмана[12][14][17], они были дополнены набором собственных. При этом при выборе параметров модели основное внимание уделялось не соответствию расчета выбранных коэффициентов общепринятым методикам финансового анализа, а влияние исходного набора данных на качество обучения сети и как следствие эффективность ее прогнозирования.

k1 = Оборотный капитал/Активы

k2 = Нераспределенная прибыль/Активы

k3 = Прибыль до налогообложения/Активы

k4 = Объем продаж/Активы

k5 = Рыночная стоимость собственного капитала/Активы

K6 = Чистый денежный поток/Активы

K7 = Чистый денежный поток/Общая задолженность

K8 = Оборачиваемость активов/ Текущие обязательства

K9 = Оборачиваемость активов/Выручка

K10 = Общая задолженность/Активы

Как уже было сказано, коэффициенты обучения и инерции являются параметрами алгоритма обратного распространения и определяют скорость и точность определения весов, минимизирующих ошибку предсказания. Большие значения этих параметров позволяют алгоритму сходиться за меньшее число итераций, но при этом возрастает риск “проскочить” оптимальное решение. Слишком малые значения, хотя и позволяют с высокой вероятностью определять глобальный минимум, неоправданно увеличивают время работы алгоритма. Эксперементальным путем были подобраны оптимальные значения для данной конфигурации многослойного персептрона.

В рассматриваемой задаче прогнозирования бакротства наряду с выбором модели и конфигурации важным моментом является сбор статистики по предприятиям. При этом необходимо понимать, что выбор тех или иных предприятий зависит от цели обучения. При рассмотрении компаний одной отрасли на фиксированном временном отрезке вероятно, что сеть хорошо научится предсказывать финансовую несостоятельность предприятий данного типа в рассматриваемом временном диапазоне, но будет несостоятельна в оценке компаний других областей. В случае обобщенной выборки (предпрития разных отраслей в произвольном временном периоде) точность прогнозирования будет падать.

Данная конфигурация нейронной сети разрабатывалась для промышленных предприятий. Ее меньшая пригодность для прогнозирования банкротства компании финансового сектора вызвана особенностями ведения бухгалтерского учета, и как следствие ряд входных параметров разработанной модели не несет в себе значимой информации для организаций непромышленной сферы.

В качестве исходных данных бралась финансовая отчетность 100 компаний (данные о 50 компаниях выступали в качестве данных для обучения, для тестирования модели 100 компаний были разбиты на 2 множества – обучающее множество и тестирующее множество). Деятельность организаций рассматривалась в период с 1993 по 1997 год, что позволило включить в модель влияние различных внешних факторов. Соотношение обанкротившихся и финансово устойчивых предприятий в выборке было оптимальным: 50/50, что является исключительно важным для корректности обучения нейронной сети. Если бы в исходных данных преобладали благополучные предприятия, сеть могла бы “подумать”, что высокую вероятность правильного прогноза легко получить простым предположением о том, что каждое предприятие жизнеспособно в рассматриваемом периоде.

Для оценки правильности модели была собрана статистика по фирмам за 3 года до их банкротства (для благополучных компаний – за 3 года предшествующих произвольной дате существования предприятия) и нейронная сеть обучена на данных финансовой очетности каждого года. Целью теста было увидеть насколько хорошо модель пронозирует состояние организации через год, через 2 года и через 3 года. Как уже было сказано, обучение проводилось с использованием данных отчетности 50 предприятий, эти же данные были включены в обучающее множество, на котором проводился первый этап тестирования. На основании финансовой информации об оставшихся 50 предприятиях было сформировано тестирующее покрывающее множество, которое использовалось для оценки “обобщающей способности” модели. Были получены следующие результаты:

	Корректность прогноза
	Обучающее множество			Тестирующее множество
	Общий показатель	Для благополучных компаний	Для несостоятельных	Общий показатель	Для благополучных компаний	Для несостоятельных
Год 0	98%	100%	96%	88%	81%	96%
Год 1	88%	88%	88%	69%	58%	81%
Год 2	90%	100%	81%	62%	65%	58%

Как и ожидалось, модель показала высокие результаты для обучающего множества и значительно более низкие для тестирующего. Особенно интересным в анализе результатов прогнозирования для компаний из тестируюзего множества, представляется факт высокой вероятности предсказания банкротства в первые 2 года. Требуется дальнейшее исследование для определения причин этого явления.