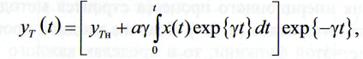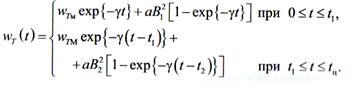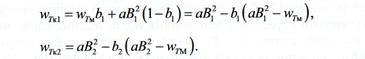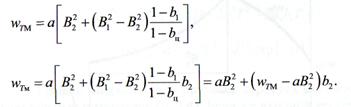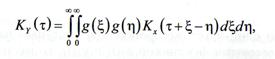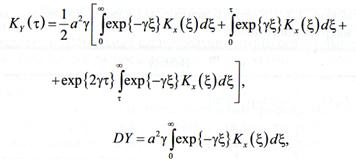ВСТУПЛЕНИЕ
Проблемы
ЭМС существуют во всех сферах деятельности человека - везде, где используются
электрический ток, магнитные и электрические поля. Здесь есть аналогия с
проблемами экологии, причем не внешняя, а достаточно глубокая ‒
методологическая как и в охране окружающей среды, существует недооценка проблем
ЭМС, что ведет к мало контролируемого количественного накопления помех ЭМС,
которое неминуемо создает качественно новую критическую ситуацию с уровнями и
составом загрязнений. Расходы на преодоление такой ситуации будут существенно
выше, чем расходы на ее предотвращение.
Одним
из основных требований до систем электроснабжения есть обеспечение ЭМС.
Завышение оценок ЭМС приводит к необоснованному увеличению капиталовложений, а
занижение ‒ к убыткам от ухудшения качества продукции, уменьшения срока
службы электрооборудования, дополнительных расходов электроэнергии, а в ряде
случаев ‒ к ухудшению здоровья человека и уменьшения производительности
труда. В связи с этим высокие требования предъявляются к достоверности методов
оценивания ЭМС как на стадии проектирования, так и в эксплуатации систем
электропотребления.
В
стандарте дано определение ЭМС технических средств: способность технического
средства функционировать с заданным качеством в заданной электромагнитной среде
и не создавать электромагнитных помех, которые являются недопустимыми для
других технических средств. Относительно задач электропотребления электрической
средой есть система электроснабжения, а техническими средствами ‒
электрооборудование, которое принимает полезный сигнал: напряжение. Напряжение
искажают кондуктивные помехи, которые распространяются по проводам. В связи с
этим под ЭМС в узком смысле следует понимать способность электрооборудования
нормально функционировать в системе электроснабжения и не создавать в ней
кондуктивных помех, которые являются недопустимыми для другого
электрооборудования.
Задачи
обеспечения ЭМС решаются на стадии проектирования и в эксплуатации. Это
нуждается в разработке методов расчета и измерения показателей ЭМС - величинах,
которые количественно характеризуют влияние помех на электрооборудование.
Достоверность
оценивания ЭМС обеспечивается адекватным математическим описанием
(моделированием) как электроприемников, так и систем электроснабжения. Уровни
сложности моделей определяются условиями конкретных задач, причем существуют
границы упрощения, за которыми теряется смысл. Отсутствие знаний порождает
иллюзию того, что можно обойтись интуитивно ясными показателями ЭМС, не
занимаясь теоретическими построениями, которые якобы являются ненужными
«рядовому инженеру». Напротив, парадокс как раз и заключается в потому, что
необходимая для практики простота измерений и расчетов достигается на основе
исследований в рамках сложных, но корректных моделей.
Значительную
роль в решении проблем ЭМС играют стандарты на показатели ЭМС. За целями их
условно будем разделять на сетевых и потребительских. Сетевые стандарты
устанавливают требования к ЭМС в точках общего присоединения энергосистемы и
потребителя, что позволяет обнаружить нарушителя ЭМС и применить к нему санкции
. Сетевые нормы не могут учитывать особенности каждого вида оборудования,
потому или являются условными, или относятся к одному «стандартному» объекту.
Потребительские
стандарты устанавливают нормы на зажимах конкретного электрооборудования. Требования
стандартов определяют технические ограничения: если нормы нарушаются, то без
дополнительных обоснований нужно улучшать ЭМС. Однако это может быть
целесообразным и при выполнении норм стандартов ‒ за экономическими
критериями, потому показатели ЭМС должны позволять оценивать убытки от помех
для существующего электрооборудования.
В
большинстве случаев помехи по времени изменяются быстро, что нуждается в
использовании динамических моделей ЭМС. Уровень сложности моделей зависит от
целей их использования. По аналогии с теорией электрических нагрузок
электроприемники разделим на массовые и уникальные. Модели ЭМС массовых
электроприемников выбираются предельно простыми, качественно однотипными,
которые отличаются лишь числовыми значениями параметров. Модели уникальных
электроприемников могут быть сложными, однако принципы оценивания ЭМС являются
одинаковыми.
Входными
процессами в моделях ЭМС являются кондуктивные помехи. Выбор их математического
описания (математической модели) определяется условиями конкретных задач. Если
случайные факторы несущественно влияют на результаты исследований, используют
детерминированные модели. В большинстве задач пренебрегать случайными факторами
нельзя, потому нужно использовать вероятностные модели. Более того,
детерминированные процессы в некоторых случаях целесообразно рассматривать как
частный случай вероятностных процессов.
Практическое
использование теории вероятностей возможно потому, что случайным явлениям
присущие неслучайные закономерности, которые существуют объективно. Вопросы
относительно причин их возникновения относятся к философии. Теория же
вероятностей оперирует детерминированными величинами и функциями, которые
отображают закономерности. Потому в вероятностных моделях, как и в моделях из
других разделов математики, нет ничего необычного. Отмена заключается лишь в
трактовке результатов: вероятностные характеристики имеют статистический смысл,
поскольку оказываются при многократном воссоздании опроса. Предусмотреть
следствие одного наблюдения невозможно. Именно статистическая стойкость
является условием корректности теории вероятностей. Если она отсутствует,
процесс является неопределенным, а не случайным.
Практическое
значение вероятностных методов заключается в том, что они за характеристиками
простых случайных явлений, которые являются известными, позволяют
прогнозировать характеристики более сложных неизвестных явлений. Эффективность
теории вероятностей предопределена тем, что из широкого диапазона возможных
значений случайной величины выделяется более узкий диапазон практически
достоверных значений, на который рассчитываются средства оптимизации и
стабилизации параметров режима. Тем самым достигается экономия средств на эти
средства.
В
проектировании начальными данными есть графика нагрузок отдельных
электроприемников или их характеристики. Эти данные получают экспериментально
или из технологических расчетов. В первом случае модель индивидуальной нагрузки
является вероятностной, потому что в действующих учреждениях неминуемыми
являются случайные отклонения от расчетного режима. Исключения составляют
автоматизированные объекты. Во втором случае чаще всего используют
детерминированные модели, которые отвечают периодическому
повторно-кратковременному режиму. Электроприемники работают независимо, потому
суммарный график является случайным. Его характеристики рассчитываются методами
теории вероятностей. Такая же схема расчетов применяется и при решении задач ЭМС.
В
действующих электрических системах можно получить случайные графики параметров
режима, которые используются для оценивания соответствия показателей ЭМС
стандартам и расчету вероятностных убытков от нарушения ЭМС.
Принцип
моделирования ЭМС
Развитие теории ЭМС начиналось с
нормирования показателей качества напряжения, относящихся к помехе x(t). При
этом не учитывалось, что одна и та же помеха на разные электроприемники
воздействует по разному.
Был сформулирован принцип моделирования объектов, согласно
которому оценку качества электроэнергии предлагалось производить не по
характеристикам помехи x(t), а по характеристикам реакции y(t) объекта на
помеху. Для этой цели необходимо моделировать рассматриваемый объект.
По аналогии с [2] блок ВФ (рис. 1), моделирующий реакцию, будем
называть взвешивающим фильтром. Квадратор 1 учитывает то обстоятельство, что
воздействие помехи зависит от мощности реакции. Инерционность объекта моделируется
инерционным звеном 2, на выходе которого протекает квадратичный инерционный
процесс wT(t). На выходе модели предусмотрен блок ПЭ вычисления
показателя ЭМС ψ.
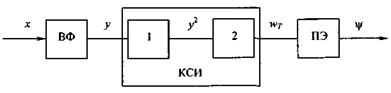
Рис. 1. Модель
воздействия помехи
Если помеха изменяется медленно или инерционность объекта мала,
то переходными процессами в блоках модели можно пренебречь. В этом случае
реакция и помеха связаны функциональной зависимостью которая является
статической характеристикой объекта. Соответственно и модель ЭМС будет
статической.
Звенья 1 и 2 образуют блок КСИ квадратичного инерционного
сглаживания ( squaring and smoothing). Этот блок условно
именовался энергетическим.
В большинстве случаев, особенно в системах электроснабжения с
резкопеременными нагрузками, помехи изменяются быстро, что требует
использования динамических моделей ЭМС. В них реакция и помеха связаны между
собой дифференциальными или интегральными уравнениями. Учет переходных
процессов здесь принципиально необходим.
Оценивание ЭМС в рамках моделей стандартных электроприемников вполне
оправдано при разграничении ответственности за ухудшение качества напряжения
между энергоснабжающей компанией и потребителями электроэнергии на границах их
балансовой принадлежности. Актуальность такого контроля возрастет в случае
введения экономических санкций за несоблюдение норм стандартов - по примеру
России .
Иначе обстоит дело с оцениванием ЭМС в системах электроснабжения
проектируемых и действующих предприятий, так как удовлетворительный для
стандартного электроприемника уровень требований для конкретного
электроприемника может оказаться завышенным или заниженным. В первом случае
стремление к выполнению норм приводит к неоправданным затратам на нормализацию
ЭМС, а во втором - к ущербу от плохого качества напряжения. В связи с этим
необходимо разрабатывать модели ЭМС конкретных электроприемников.
Моделирование
инерционности
Модели ЭМС должны отражать основные
свойства объектов, но быть предельно простыми. Инерционность объекта часто
достаточно моделировать инерционным звеном первого порядка, постоянная времени
Т которого совпадает с постоянной инерции объекта. В этом случае процессы на
входе и выходе блока КСИ связаны дифференциальным уравнением
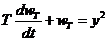
image002.gif
Обозначив через 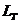 оператор инерционного
сглаживания, запишем в компактном виде
оператор инерционного
сглаживания, запишем в компактном виде
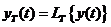
Квадратичный инерционный процесс 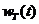 имеет размерность
квадрата реакции. В связи с этим удобно использовать приведенный инерционный
процесс
имеет размерность
квадрата реакции. В связи с этим удобно использовать приведенный инерционный
процесс
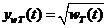
размерность ординат которого совпадает с
размерностью ординат реакции.
Инерционное
сглаживание
Инерционные звенья используются для
моделирования инерционности объектов, а также в методе парциальных реакции. Рассмотрим вначале инерционное сглаживание
без квадратора, считая коэффициент передачи а звена отличным от единицы
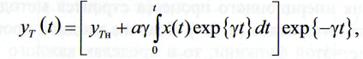
При квадратичном инерционном сглаживании
на вход звена подается 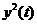 . Если исходный график является
ступенчатым, то формула для квадратичного инерционного сглаживания
. Если исходный график является
ступенчатым, то формула для квадратичного инерционного сглаживания
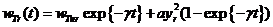
График
инерционного процесса строится методом последовательных
интервалов. Если же входной процесс задан в виде
решетчатой функции, то в пределах каждого шага дискретизации нет необходимости в построении графика инерционного процесса ‒ достаточно вычислять лишь конечные
ординаты.
Для периодических графиков сразу
находится стационарное решение.. После квадратора график сохраняет
форму, но величины ступеней возводятся в квадрат.
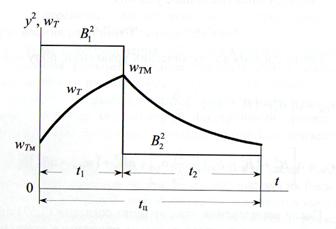
Рис.2
Найдем вначале наибольшую wTм наименьшую wTм ординаты
квадратичного инерционного процесса. Для этого запишем выражения:
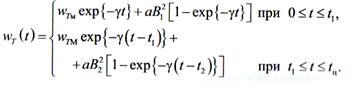
Обозначив через:
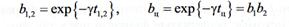
подставив
абсциссы концов участков, получим формулы для конечных ординат
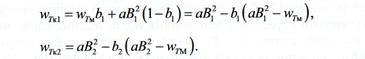
Сюда добавим граничные условия

Решая систему алгебраических уравнений,
получим:
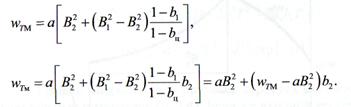
После
определения этих ординат строится график квадратичного инерционного процесса в
стационарном состоянии (рис. 2).
Вычисление
корреляционных функции по формулам вида
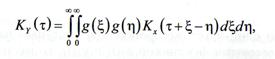
усложнено тем, что корреляционная функция входного
процесса содержит абсолютные значения аргумента. В результате приходится
различать области, где 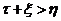 и
и 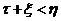 . Преобразованием осей координат получены
формулы:
. Преобразованием осей координат получены
формулы:
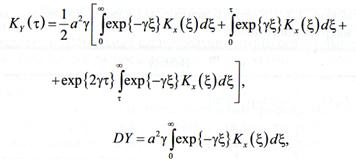
в некоторых
переменная интегрирования положительна. После интегрирования величина 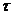 т заменяется на
т заменяется на 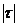 .
.
В случае
преобразования 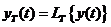 под
Кх(
под
Кх(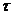 )
и понимаются корреляционная функция и стандарт реакции ВФ, а под выходным
процессом ‒ инерционный процесс. При преобразовании
)
и понимаются корреляционная функция и стандарт реакции ВФ, а под выходным
процессом ‒ инерционный процесс. При преобразовании 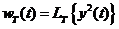 под Кх(
под Кх(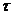 ) ‒
корреляционная функция квадрата реакции, а выходным является квадратичный
инерционный процесс. Конечные формулы для разных входных процессов приведены в
табл. 1.
) ‒
корреляционная функция квадрата реакции, а выходным является квадратичный
инерционный процесс. Конечные формулы для разных входных процессов приведены в
табл. 1.
Таблица 1 ‒ Корреляционные
функции и дисперсии на выходе инерционного звена

Сглаживающее
действие инерционного звена наглядно проявляется при входном белом шуме: его
дисперсия бесконечна, а после инерционного преобразования становится конечной.
Во всех случаях инерционные дисперсии монотонно убывают с увеличением
постоянной инерции, стремясь к нулю .